2021—2022学年华东师大版九年级数学下册27.1.2第1课时圆心角、弧、弦的关系分层训练(word版含简单答案)
文档属性
| 名称 | 2021—2022学年华东师大版九年级数学下册27.1.2第1课时圆心角、弧、弦的关系分层训练(word版含简单答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 214.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 10:49:03 | ||
图片预览

文档简介
27.1.2 第1课时 圆心角、弧、弦的关系
【基础练习】
知识点 1 圆心角、弧、弦的关系
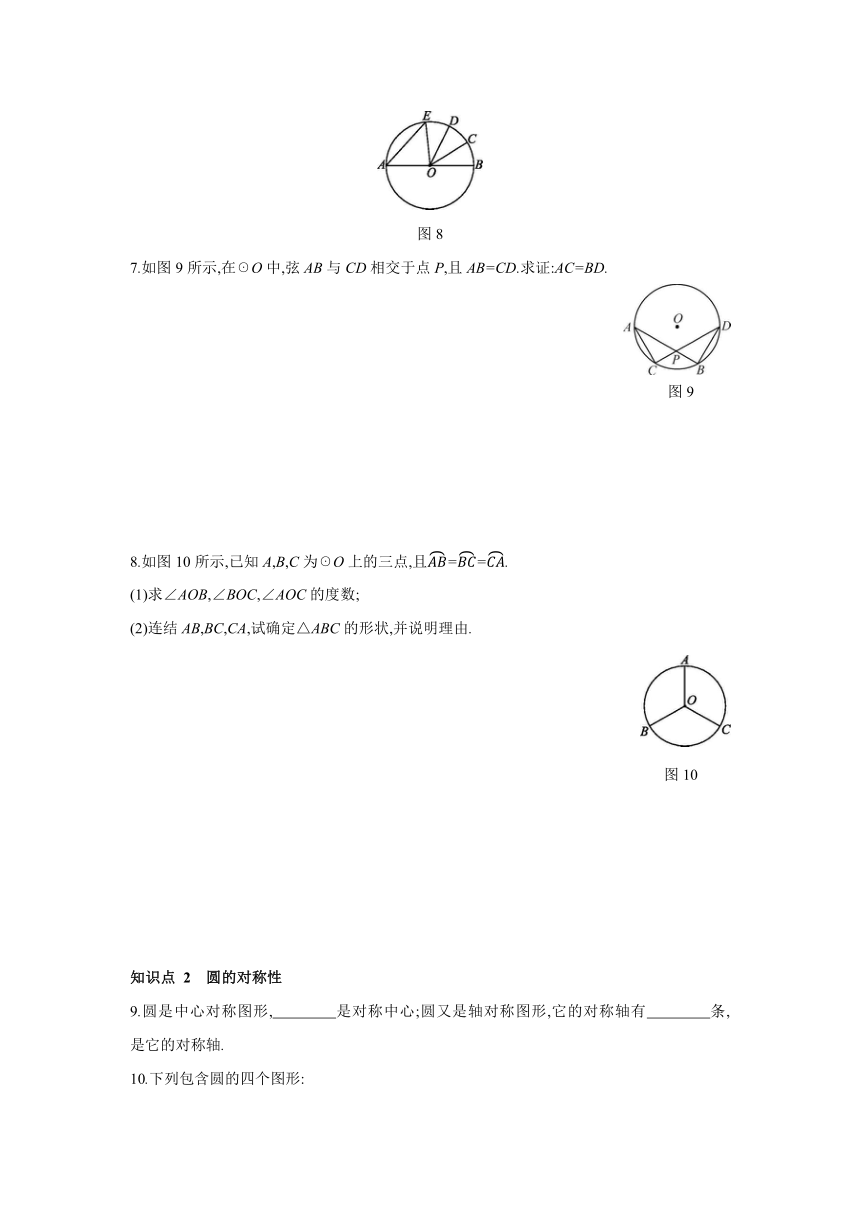
1.如图所示,已知☉O中,AB,CD是弦,根据条件填空:
(1)若AB=CD,则 , ;
(2)若=,则 , ;
(3)若∠AOB=∠COD,则 , .
2.在同圆或等圆中,下列说法错误的是 ( )
A.相等的弦所对的弧相等
B.相等的弦所对的圆心角相等
C.相等的圆心角所对的弧相等
D.相等的圆心角所对的弦相等
3.如图,AB是圆O的直径,BC,CD,DA是圆O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.135°
4.如图6,AB,CD是☉O的直径,=,若∠AOE=32°,则∠COE的度数是 .
图6 图7
5.如图7,AB为☉O的直径,△PAB的边PA,PB与☉O的交点分别为C,D.若==,则∠P的大小为 度.
6.如图8,AB是☉O的直径,==,∠COD=32°,则∠AEO的度数为 .
图8
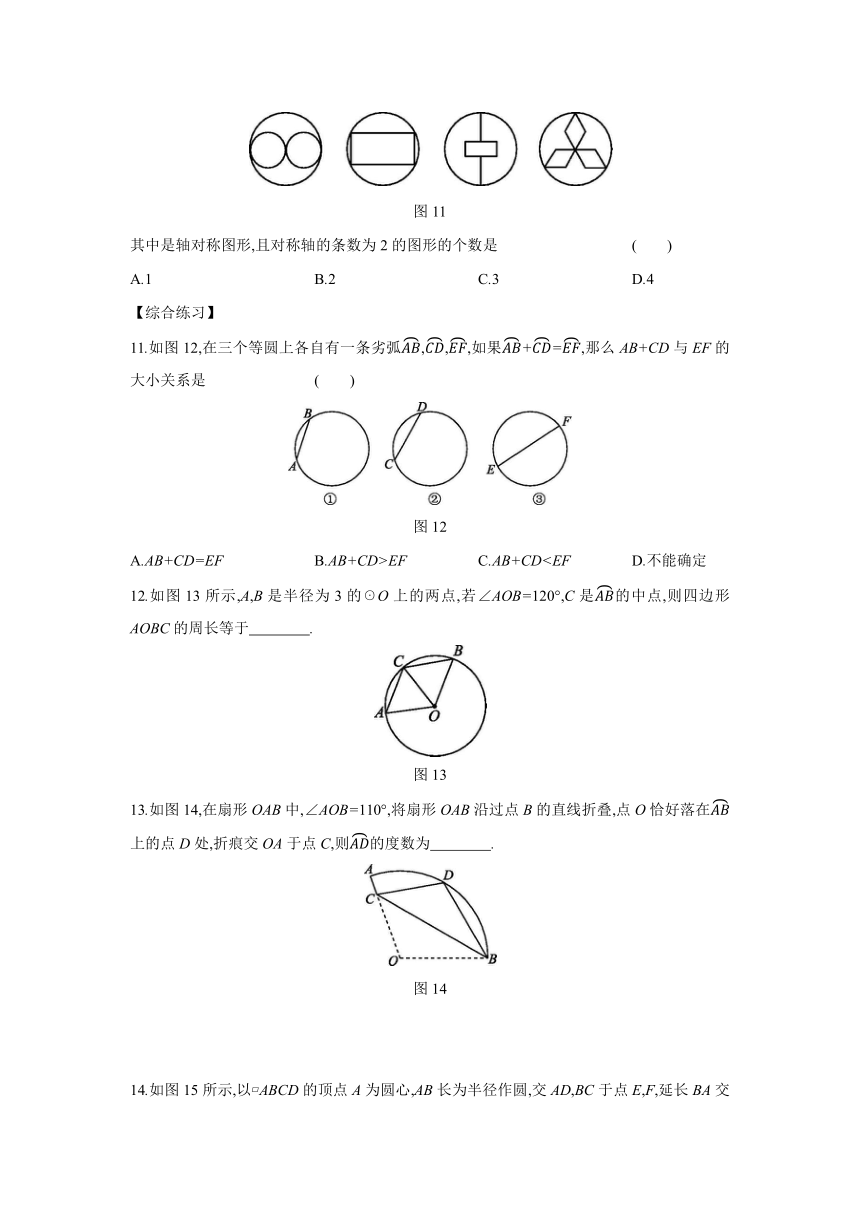
7.如图9所示,在☉O中,弦AB与CD相交于点P,且AB=CD.求证:AC=BD.
图9
8.如图10所示,已知A,B,C为☉O上的三点,且==.
(1)求∠AOB,∠BOC,∠AOC的度数;
(2)连结AB,BC,CA,试确定△ABC的形状,并说明理由.
图10
知识点 2 圆的对称性
9.圆是中心对称图形, 是对称中心;圆又是轴对称图形,它的对称轴有 条, 是它的对称轴.
10.下列包含圆的四个图形:
图11
其中是轴对称图形,且对称轴的条数为2的图形的个数是 ( )
A.1 B.2 C.3 D.4
【综合练习】
11.如图12,在三个等圆上各自有一条劣弧,,,如果+=,那么AB+CD与EF的大小关系是 ( )
图12
A.AB+CD=EF B.AB+CD>EF C.AB+CD12.如图13所示,A,B是半径为3的☉O上的两点,若∠AOB=120°,C是的中点,则四边形AOBC的周长等于 .
图13
13.如图14,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则的度数为 .
图14
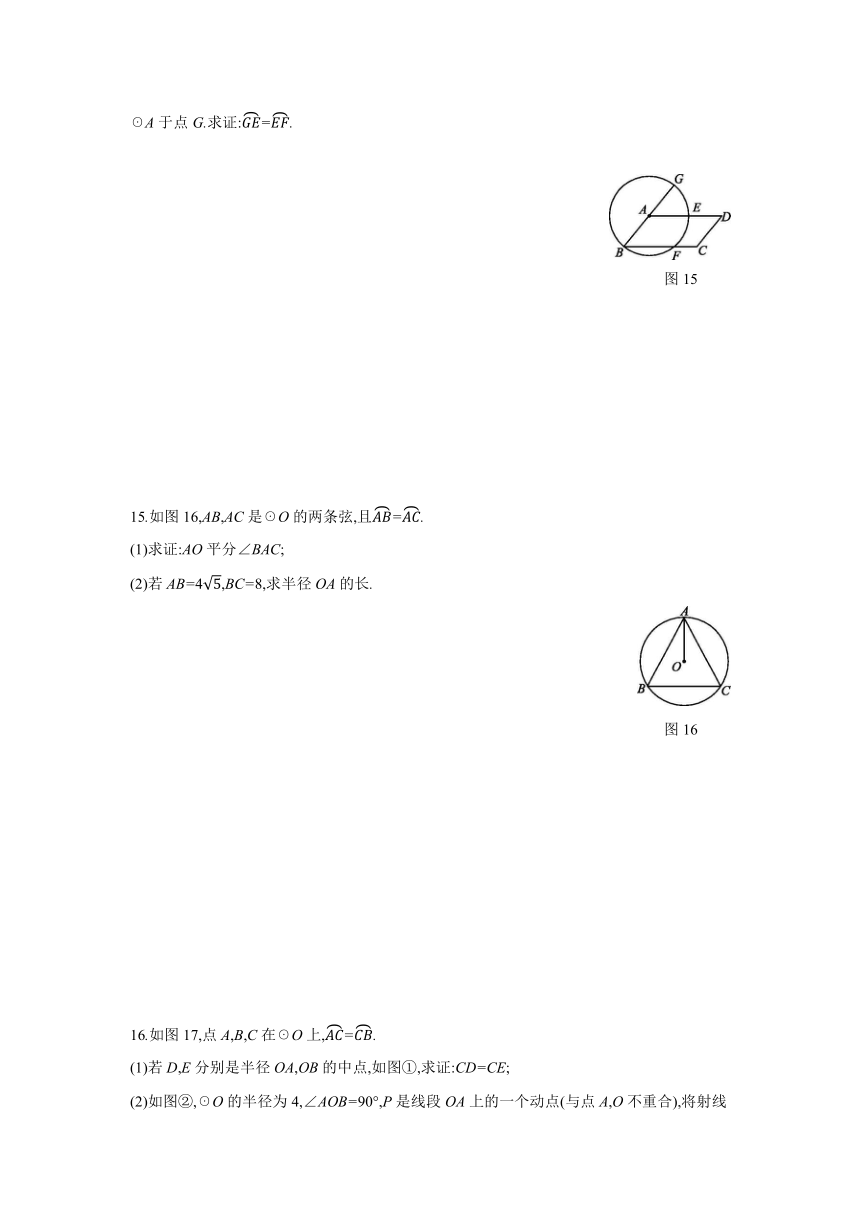
14.如图15所示,以 ABCD的顶点A为圆心,AB长为半径作圆,交AD,BC于点E,F,延长BA交☉A于点G.求证:=.
图15
15.如图16,AB,AC是☉O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
图16
16.如图17,点A,B,C在☉O上,=.
(1)若D,E分别是半径OA,OB的中点,如图①,求证:CD=CE;
(2)如图②,☉O的半径为4,∠AOB=90°,P是线段OA上的一个动点(与点A,O不重合),将射线CP绕点C逆时针旋转90°,与OB相交于点Q,连结PQ,求出PQ的最小值.
图17
27.1.2 第1课时 圆心角、弧、弦的关系
1.(1)= ∠AOB=∠COD
(2)∠AOB=∠COD AB=CD
(3)= AB=CD
2.A
3.C
4.64°
5.60
6.48°
7.证明:∵AB=CD,
∴=,
∴-=-,
即=,
∴AC=BD.
8.解:(1)∵==,
∴∠AOB=∠BOC=∠AOC=120°.
(2)△ABC是等边三角形.
理由:∵==,
∴AB=BC=CA,
∴△ABC是等边三角形.
9.圆心 无数 经过圆心的任意一条直线(或任意一条直径所在的直线)
10.C
11.B
12.12
13.50°
14.证明:如图,连结AF.
∵AB=AF,
∴∠ABF=∠AFB.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AFB,∠GAE=∠ABF,
∴∠GAE=∠EAF,
∴=.
15.解:(1)证明:如图,连结OB,OC.
在△AOB和△AOC中,
∵AB=AC,OB=OC,OA=OA,
∴△AOB≌△AOC,
∴∠1=∠2,即AO平分∠BAC.
(2)如图,延长AO交BC于点E.
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,BE=CE=BC=4.
在Rt△ABE中,AE==8.
设OA=x,则OB=x,OE=8-x.
在Rt△BOE中,由勾股定理,得OB2=BE2+OE2,即x2=42+(8-x)2,解得x=5,
∴半径OA的长为5.
16.解:(1)证明:如图①,连结CO.
∵=,
∴∠AOC=∠BOC.
∵D,E分别是半径OA,OB的中点,
∴OD=OA,OE=OB,
∴OD=OE.
在△ODC和△OEC中,
∵OD=OE,∠AOC=∠BOC,OC=OC,
∴△ODC≌△OEC,
∴CD=CE.
(2)连结CO.
当CP⊥OA时,∵∠AOB=90°,∠PCQ=90°,
∴∠CQO=90°,即CQ⊥OB.
∵∠AOC=∠BOC,
∴CP=CQ.
当CP与OA不垂直时,
如图②,过点C作CM⊥OA,CN⊥OB,垂足分别为M,N.
∵∠AOC=∠BOC,∴CM=CN.
∵∠AOB=∠CMO=∠CNO=90°,
∴∠MCN=90°.
又∵∠PCQ=90°,∴∠PCM=∠QCN.
又∵∠PMC=∠QNC=90°,
∴△PCM≌△QCN,
∴CP=CQ,∴PQ=CP,
∴当CP取得最小值,即CM的长时,PQ有最小值,
∴PQ=CP≥CM=CO=4,故PQ的最小值为4.
【基础练习】
知识点 1 圆心角、弧、弦的关系
1.如图所示,已知☉O中,AB,CD是弦,根据条件填空:
(1)若AB=CD,则 , ;
(2)若=,则 , ;
(3)若∠AOB=∠COD,则 , .
2.在同圆或等圆中,下列说法错误的是 ( )
A.相等的弦所对的弧相等
B.相等的弦所对的圆心角相等
C.相等的圆心角所对的弧相等
D.相等的圆心角所对的弦相等
3.如图,AB是圆O的直径,BC,CD,DA是圆O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.135°
4.如图6,AB,CD是☉O的直径,=,若∠AOE=32°,则∠COE的度数是 .
图6 图7
5.如图7,AB为☉O的直径,△PAB的边PA,PB与☉O的交点分别为C,D.若==,则∠P的大小为 度.
6.如图8,AB是☉O的直径,==,∠COD=32°,则∠AEO的度数为 .
图8
7.如图9所示,在☉O中,弦AB与CD相交于点P,且AB=CD.求证:AC=BD.
图9
8.如图10所示,已知A,B,C为☉O上的三点,且==.
(1)求∠AOB,∠BOC,∠AOC的度数;
(2)连结AB,BC,CA,试确定△ABC的形状,并说明理由.
图10
知识点 2 圆的对称性
9.圆是中心对称图形, 是对称中心;圆又是轴对称图形,它的对称轴有 条, 是它的对称轴.
10.下列包含圆的四个图形:
图11
其中是轴对称图形,且对称轴的条数为2的图形的个数是 ( )
A.1 B.2 C.3 D.4
【综合练习】
11.如图12,在三个等圆上各自有一条劣弧,,,如果+=,那么AB+CD与EF的大小关系是 ( )
图12
A.AB+CD=EF B.AB+CD>EF C.AB+CD
图13
13.如图14,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则的度数为 .
图14
14.如图15所示,以 ABCD的顶点A为圆心,AB长为半径作圆,交AD,BC于点E,F,延长BA交☉A于点G.求证:=.
图15
15.如图16,AB,AC是☉O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
图16
16.如图17,点A,B,C在☉O上,=.
(1)若D,E分别是半径OA,OB的中点,如图①,求证:CD=CE;
(2)如图②,☉O的半径为4,∠AOB=90°,P是线段OA上的一个动点(与点A,O不重合),将射线CP绕点C逆时针旋转90°,与OB相交于点Q,连结PQ,求出PQ的最小值.
图17
27.1.2 第1课时 圆心角、弧、弦的关系
1.(1)= ∠AOB=∠COD
(2)∠AOB=∠COD AB=CD
(3)= AB=CD
2.A
3.C
4.64°
5.60
6.48°
7.证明:∵AB=CD,
∴=,
∴-=-,
即=,
∴AC=BD.
8.解:(1)∵==,
∴∠AOB=∠BOC=∠AOC=120°.
(2)△ABC是等边三角形.
理由:∵==,
∴AB=BC=CA,
∴△ABC是等边三角形.
9.圆心 无数 经过圆心的任意一条直线(或任意一条直径所在的直线)
10.C
11.B
12.12
13.50°
14.证明:如图,连结AF.
∵AB=AF,
∴∠ABF=∠AFB.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AFB,∠GAE=∠ABF,
∴∠GAE=∠EAF,
∴=.
15.解:(1)证明:如图,连结OB,OC.
在△AOB和△AOC中,
∵AB=AC,OB=OC,OA=OA,
∴△AOB≌△AOC,
∴∠1=∠2,即AO平分∠BAC.
(2)如图,延长AO交BC于点E.
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,BE=CE=BC=4.
在Rt△ABE中,AE==8.
设OA=x,则OB=x,OE=8-x.
在Rt△BOE中,由勾股定理,得OB2=BE2+OE2,即x2=42+(8-x)2,解得x=5,
∴半径OA的长为5.
16.解:(1)证明:如图①,连结CO.
∵=,
∴∠AOC=∠BOC.
∵D,E分别是半径OA,OB的中点,
∴OD=OA,OE=OB,
∴OD=OE.
在△ODC和△OEC中,
∵OD=OE,∠AOC=∠BOC,OC=OC,
∴△ODC≌△OEC,
∴CD=CE.
(2)连结CO.
当CP⊥OA时,∵∠AOB=90°,∠PCQ=90°,
∴∠CQO=90°,即CQ⊥OB.
∵∠AOC=∠BOC,
∴CP=CQ.
当CP与OA不垂直时,
如图②,过点C作CM⊥OA,CN⊥OB,垂足分别为M,N.
∵∠AOC=∠BOC,∴CM=CN.
∵∠AOB=∠CMO=∠CNO=90°,
∴∠MCN=90°.
又∵∠PCQ=90°,∴∠PCM=∠QCN.
又∵∠PMC=∠QNC=90°,
∴△PCM≌△QCN,
∴CP=CQ,∴PQ=CP,
∴当CP取得最小值,即CM的长时,PQ有最小值,
∴PQ=CP≥CM=CO=4,故PQ的最小值为4.
