2021—2022学年华东师大版九年级数学下册27.1.3 圆周角 分层训练(Word版含答案)
文档属性
| 名称 | 2021—2022学年华东师大版九年级数学下册27.1.3 圆周角 分层训练(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 214.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 00:00:00 | ||
图片预览



文档简介
27.1.3 圆周角
知识点 1 圆周角的概念
1.下列各图中的∠1为圆周角的是 ( )
2.如图,在图中标出的4个角中,圆周角有 个.
知识点 2 圆周角定理
3.如图4,AB,BC都是☉O的弦,∠ABC=40°,则∠AOC的度数为 ( )
图4
A.50° B.60° C.80° D.90°
4.如图5,AB是☉O的直径,C,D是圆上两点,且∠AOC=126°,则∠CDB等于 ( )
A.54° B.64° C.27° D.37°
图5 图6
5.[2020·巴中] 如图6,在☉O中,点A,B,C在圆上,∠ACB=45°,AB=2,则☉O的半径OA的长是 ( )
A. B.2 C.2 D.3
6.如图7所示,☉O的直径CD过弦EF的中点G,∠GEO=46°,则∠DCF= .
图7
7.如图8,△ABC的三个顶点都在☉O上,直径AD=6 cm,∠DAC=2∠B,求AC的长.
图8
知识点 3 圆周角定理的推论
8.从下列三角尺与圆弧的位置关系中,可判断圆弧为半圆的是 ( )
图9
9.如图10,已知AB是半圆O的直径,∠BAC=20°,D是上任意一点,则∠D的度数是 .
图10
【能力提升】
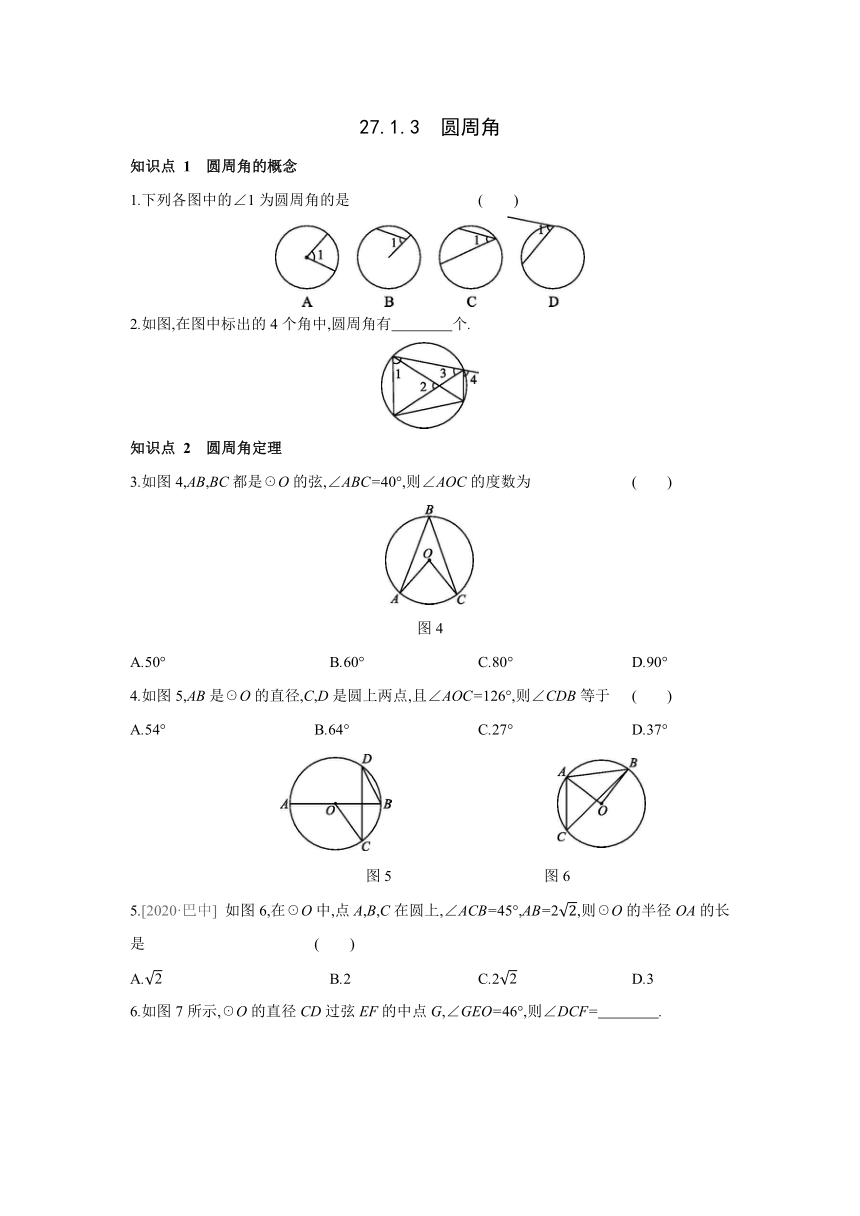
10.如图11,点D(0,3),O(0,0),C(4,0)在☉A上,BD是☉A的一条弦,则cos∠OBD等于 ( )
图11
A. B. C. D.
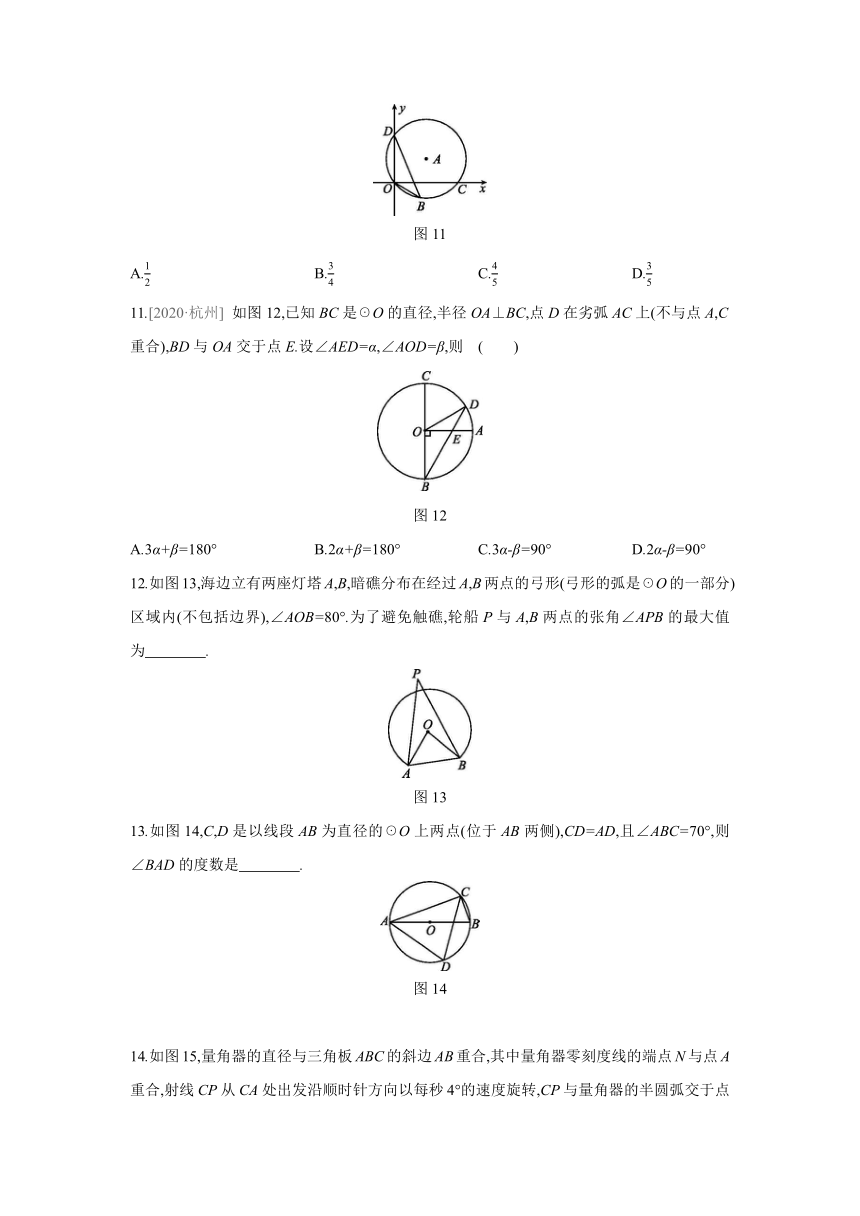
11.[2020·杭州] 如图12,已知BC是☉O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则 ( )
图12
A.3α+β=180° B.2α+β=180° C.3α-β=90° D.2α-β=90°
12.如图13,海边立有两座灯塔A,B,暗礁分布在经过A,B两点的弓形(弓形的弧是☉O的一部分)区域内(不包括边界),∠AOB=80°.为了避免触礁,轮船P与A,B两点的张角∠APB的最大值为 .
图13
13.如图14,C,D是以线段AB为直径的☉O上两点(位于AB两侧),CD=AD,且∠ABC=70°,则∠BAD的度数是 .
图14
14.如图15,量角器的直径与三角板ABC的斜边AB重合,其中量角器零刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒4°的速度旋转,CP与量角器的半圆弧交于点E,第18秒时,点E在量角器上对应的读数是 度.
图15
15.如图16,在△ABC中,AB=BC,以AB为直径的☉O交AC于点D,交BC于点E,连结ED.
(1)求证:ED=DC;
(2)若CD=6,EC=4,求AB的长.
图16
16.九年级学生小刚是一个喜欢看书的好学生,他在家里突然看到爸爸的初中数学书上居然还有一个相交弦定理(圆内的两条相交弦,被交点分成的两条线段长的积相等),非常好奇,仔细阅读原来这个定理用几何语言表述如下:如图17①,☉O的弦AB,CD交于点P,则PA·PB=PC·PD.小刚很想知道是如何证明的,可证明部分已被污损看不清了,只看到辅助线的作法:连结AC,BD.
(1)请在图①中作出辅助线,并写出详细的证明过程;
(2)小刚又看到一道课后习题:如图②,AB是☉O的一条弦,P是AB上一点,AB=10 cm,PA=
4 cm,OP=5 cm,求☉O的半径.这道题把小刚给难住了,请乐于助人的你帮他写出详细的求解过程吧!
图17
27.1.3 圆周角
1.C 2.2
3.C 4.C
5.B
6.22°
7.解:如图,连结OC.
∵∠AOC=2∠B,∠DAC=2∠B,
∴∠AOC=∠DAC,
∴OC=AC.
又∵OA=OC,
∴△AOC是等边三角形,
∴AC=AO=AD=3 cm.
8.B
9.110°
10.C
11.D
12.40°
13.35°
14.144
15.解:(1)证明:∵A,B,E,D四点共圆,
∴∠BED+∠A=180°.
又∵∠BED+∠DEC=180°,
∴∠DEC=∠A.
∵AB=BC,
∴∠A=∠C,
∴∠DEC=∠C,
∴ED=DC.
(2)如图,连结BD.
∵AB为☉O的直径,
∴∠ADB=90°,
即BD⊥AC.
∵AB=BC,
∴AD=CD=6,
∴AC=12.
∵∠A=∠DEC,∠C=∠C,
∴△DEC∽△BAC,
∴=,
即=,解得BC=6.
∵AB=BC,∴AB=6.
16.解:(1)证明:连结AC,BD,如图①.
∵∠C=∠B,∠A=∠D,
∴△APC∽△DPB,
∴PA∶PD=PC∶PB,
∴PA·PB=PC·PD.
(2)过点P作直径CD,如图②.
设☉O的半径为R cm.
∵AB=10 cm,PA=4 cm,OP=5 cm,
∴PB=10-4=6(cm),PC=(R+5)cm,PD=(R-5)cm.
由相交弦定理,得PA·PB=PC·PD,
∴4×6=(R+5)·(R-5),
解得R=7(R=-7舍去),
∴☉O的半径为7 cm.
知识点 1 圆周角的概念
1.下列各图中的∠1为圆周角的是 ( )
2.如图,在图中标出的4个角中,圆周角有 个.
知识点 2 圆周角定理
3.如图4,AB,BC都是☉O的弦,∠ABC=40°,则∠AOC的度数为 ( )
图4
A.50° B.60° C.80° D.90°
4.如图5,AB是☉O的直径,C,D是圆上两点,且∠AOC=126°,则∠CDB等于 ( )
A.54° B.64° C.27° D.37°
图5 图6
5.[2020·巴中] 如图6,在☉O中,点A,B,C在圆上,∠ACB=45°,AB=2,则☉O的半径OA的长是 ( )
A. B.2 C.2 D.3
6.如图7所示,☉O的直径CD过弦EF的中点G,∠GEO=46°,则∠DCF= .
图7
7.如图8,△ABC的三个顶点都在☉O上,直径AD=6 cm,∠DAC=2∠B,求AC的长.
图8
知识点 3 圆周角定理的推论
8.从下列三角尺与圆弧的位置关系中,可判断圆弧为半圆的是 ( )
图9
9.如图10,已知AB是半圆O的直径,∠BAC=20°,D是上任意一点,则∠D的度数是 .
图10
【能力提升】
10.如图11,点D(0,3),O(0,0),C(4,0)在☉A上,BD是☉A的一条弦,则cos∠OBD等于 ( )
图11
A. B. C. D.
11.[2020·杭州] 如图12,已知BC是☉O的直径,半径OA⊥BC,点D在劣弧AC上(不与点A,C重合),BD与OA交于点E.设∠AED=α,∠AOD=β,则 ( )
图12
A.3α+β=180° B.2α+β=180° C.3α-β=90° D.2α-β=90°
12.如图13,海边立有两座灯塔A,B,暗礁分布在经过A,B两点的弓形(弓形的弧是☉O的一部分)区域内(不包括边界),∠AOB=80°.为了避免触礁,轮船P与A,B两点的张角∠APB的最大值为 .
图13
13.如图14,C,D是以线段AB为直径的☉O上两点(位于AB两侧),CD=AD,且∠ABC=70°,则∠BAD的度数是 .
图14
14.如图15,量角器的直径与三角板ABC的斜边AB重合,其中量角器零刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒4°的速度旋转,CP与量角器的半圆弧交于点E,第18秒时,点E在量角器上对应的读数是 度.
图15
15.如图16,在△ABC中,AB=BC,以AB为直径的☉O交AC于点D,交BC于点E,连结ED.
(1)求证:ED=DC;
(2)若CD=6,EC=4,求AB的长.
图16
16.九年级学生小刚是一个喜欢看书的好学生,他在家里突然看到爸爸的初中数学书上居然还有一个相交弦定理(圆内的两条相交弦,被交点分成的两条线段长的积相等),非常好奇,仔细阅读原来这个定理用几何语言表述如下:如图17①,☉O的弦AB,CD交于点P,则PA·PB=PC·PD.小刚很想知道是如何证明的,可证明部分已被污损看不清了,只看到辅助线的作法:连结AC,BD.
(1)请在图①中作出辅助线,并写出详细的证明过程;
(2)小刚又看到一道课后习题:如图②,AB是☉O的一条弦,P是AB上一点,AB=10 cm,PA=
4 cm,OP=5 cm,求☉O的半径.这道题把小刚给难住了,请乐于助人的你帮他写出详细的求解过程吧!
图17
27.1.3 圆周角
1.C 2.2
3.C 4.C
5.B
6.22°
7.解:如图,连结OC.
∵∠AOC=2∠B,∠DAC=2∠B,
∴∠AOC=∠DAC,
∴OC=AC.
又∵OA=OC,
∴△AOC是等边三角形,
∴AC=AO=AD=3 cm.
8.B
9.110°
10.C
11.D
12.40°
13.35°
14.144
15.解:(1)证明:∵A,B,E,D四点共圆,
∴∠BED+∠A=180°.
又∵∠BED+∠DEC=180°,
∴∠DEC=∠A.
∵AB=BC,
∴∠A=∠C,
∴∠DEC=∠C,
∴ED=DC.
(2)如图,连结BD.
∵AB为☉O的直径,
∴∠ADB=90°,
即BD⊥AC.
∵AB=BC,
∴AD=CD=6,
∴AC=12.
∵∠A=∠DEC,∠C=∠C,
∴△DEC∽△BAC,
∴=,
即=,解得BC=6.
∵AB=BC,∴AB=6.
16.解:(1)证明:连结AC,BD,如图①.
∵∠C=∠B,∠A=∠D,
∴△APC∽△DPB,
∴PA∶PD=PC∶PB,
∴PA·PB=PC·PD.
(2)过点P作直径CD,如图②.
设☉O的半径为R cm.
∵AB=10 cm,PA=4 cm,OP=5 cm,
∴PB=10-4=6(cm),PC=(R+5)cm,PD=(R-5)cm.
由相交弦定理,得PA·PB=PC·PD,
∴4×6=(R+5)·(R-5),
解得R=7(R=-7舍去),
∴☉O的半径为7 cm.
