2021-2022学年华东师大版九年级数学下册27.2.1 点与圆的位置关系 分层训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学下册27.2.1 点与圆的位置关系 分层训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 159.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 00:00:00 | ||
图片预览



文档简介
27.2.1 点与圆的位置关系
知识点 1 点与圆的位置关系
1.已知☉O的半径为6 cm,若OA=4 cm,则点A在☉O ;若OB=6 cm,则点B在☉O ;若OC=7 cm,则点C在☉O .
2.已知A为☉O外的一个点,且☉O的半径为9 cm,则线段OA的长度可能为 ( )
A.7 cm B.8 cm C.9 cm D.10 cm
3.如图1,边长为1的正方形ABCD的两条对角线相交于点O,以点A为圆心,1为半径画圆,则点O,B,C,D中,点 在圆内,点 在圆上,点 在圆外.
图1
4.[教材习题27.2第1题变式] 如图2,已知在△ABC中,AC=3,BC=4,∠C=90°,以点C为圆心作☉C,半径为r.
(1)当r在什么取值范围内时,点A,B都在☉C外
(2)当r在什么取值范围内时,点A在☉C内,点B在☉C外
图2
知识点 2 确定圆的条件
5.给定下列条件可以确定一个圆的是 ( )
A.已知圆心 B.已知半径
C.已知直径 D.已知不在同一直线上的三个点
6.如图3所示,点A,B,C在同一直线上,点M在直线AC外,经过图中的三个点作圆,可以作
个.
图3 图4
7.如图4所示,已知A,B,C三点(三点不在同一直线上),求作:☉O,使它经过A,B,C三点.(要求:尺规作图,不写作法,但要保留作图痕迹)
知识点 3 三角形的外接圆与圆的内接三角形
8.三角形的外心是三角形 的交点,其中直角三角形的外心是 的中点,锐角三角形的外心在三角形的 ,钝角三角形的外心在三角形的 .
9.如图5,若△ABC内接于半径为R的☉O,且∠A=60°,连结OB,OC,则边BC的长为 ( )
图5
A.R B.R C.R D.R
10.已知一个三角形的三边长分别为13 cm,12 cm,5 cm,则此三角形外接圆的半径为
cm.
11.如图6,在△ABC中,AB=AC.
(1)求作:△ABC的外接圆☉O(要求:尺规作图,保留作图痕迹,不写作法);
(2)若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则S☉O= .
图6
【能力提升】
12.如图7,在5×5的正方形网格中,每个小正方形的边长均为1,选取7个格点(小正方形的顶点),若以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个点在圆内,则r的取值范围是 ( )
图7
A.313.在平面直角坐标系内,O是坐标原点,点A的坐标是(3,2),点B的坐标是(3,-4).如果以点O为圆心,r为半径的☉O与直线AB相交,且点A,B中有一个点在☉O内,另一个点在☉O外,那么r的值可以取 ( )
A.5 B.4 C.3 D.2
14.如图8所示,在Rt△ABC中,∠C=90°,∠A=30°,D为AB的中点,以点C为圆心,BC长为半径画圆,则点D与☉C的位置关系是 .
图8
15.如图9,△ABC内接于☉O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若☉O的半径为2,则CD的长为 .
图9
16.平面上有☉O及一点P,P到☉O上一点的距离最长为6 cm,最短为2 cm,则☉O的半径为 .
17.已知直线l:y=x-4,点A(1,0),点B(0,2),设P为直线l上一动点,当点P的坐标为 时,过P,A,B三点不能作出一个圆.
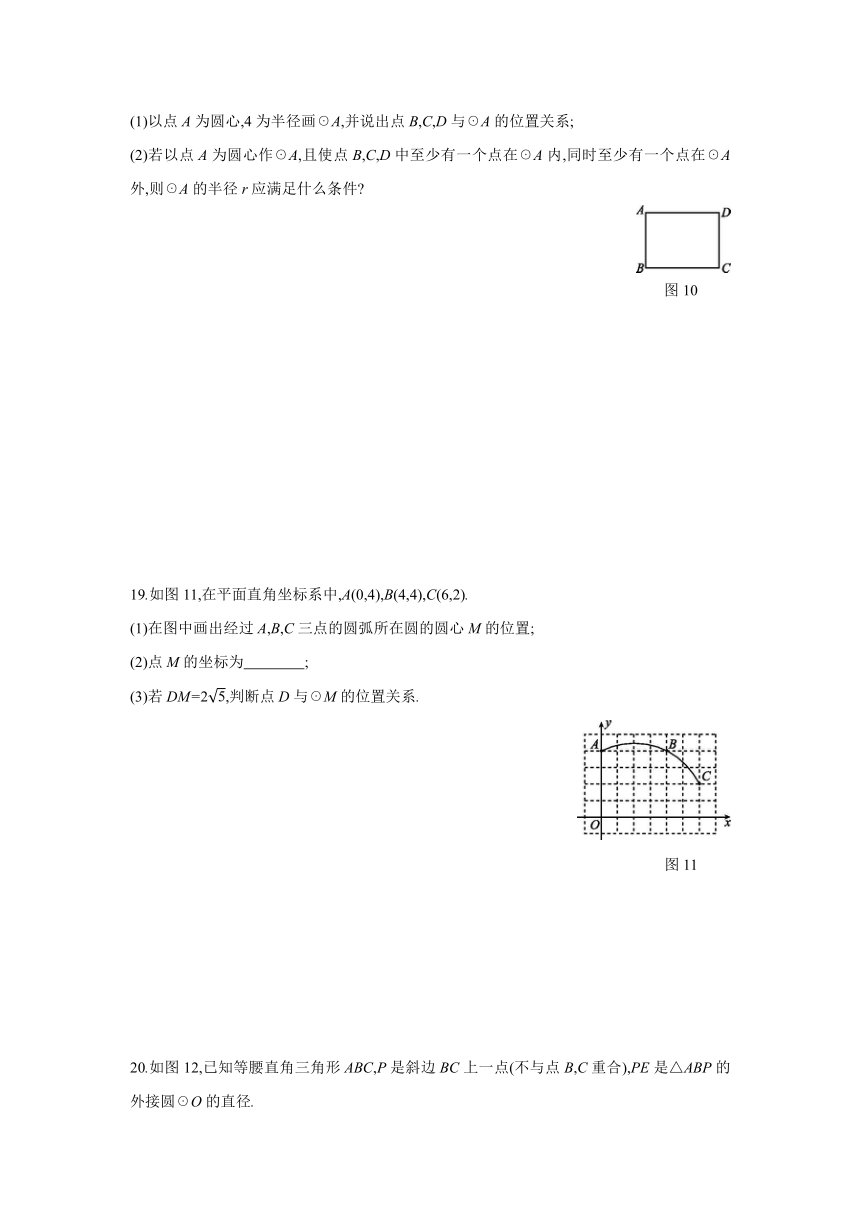
18.如图10,在矩形ABCD中,AB=3,AD=4.
(1)以点A为圆心,4为半径画☉A,并说出点B,C,D与☉A的位置关系;
(2)若以点A为圆心作☉A,且使点B,C,D中至少有一个点在☉A内,同时至少有一个点在☉A外,则☉A的半径r应满足什么条件
图10
19.如图11,在平面直角坐标系中,A(0,4),B(4,4),C(6,2).
(1)在图中画出经过A,B,C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 ;
(3)若DM=2,判断点D与☉M的位置关系.
图11
20.如图12,已知等腰直角三角形ABC,P是斜边BC上一点(不与点B,C重合),PE是△ABP的外接圆☉O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若☉O的直径为2,求PC2+PB2的值.
图12
27.2.1 点与圆的位置关系
1.内 上 外 2.D
3.O B,D C .
4.解:(1)当0(2)当35.D
6.3
7.略
8.三条边的垂直平分线 斜边 内部 外部
9.D
10.6.5
11.解:(1)如图,☉O即为所求.
(2)25π
12.D .
13.B
14.点D在☉C上 .
15.
16.2 cm或4 cm
17.(2,-2)
18.解:(1)如图.∵AB=3<4,
∴点B在☉A内.
∵AD=4,∴点D在☉A上.
连结AC,由勾股定理可求出AC=5>4,
∴点C在☉A外.
(2)∵AB19.解:(1)如图,点M即为所求.
(2)(2,0)
(3)☉M的半径AM==2.
∵DM=2,∴点D在☉M上.
20.解:(1)证明:∵△ABC是等腰直角三角形,BC是斜边,
∴∠C=∠ABC=45°,
∴∠AEP=∠ABP=45°.
∵PE是☉O的直径,
∴∠PAE=90°,
∴∠APE=∠AEP=45°,
∴AP=AE,
∴△APE是等腰直角三角形.
(2)∵∠CAB=∠PAE=90°,
∴∠CAP=∠BAE.
又∵AC=AB,AP=AE,
∴△CAP≌△BAE,
∴∠ACP=∠ABE=45°,PC=BE,
∴∠PBE=∠ABC+∠ABE=90°,
∴PC2+PB2=BE2+PB2=PE2=22=4.
知识点 1 点与圆的位置关系
1.已知☉O的半径为6 cm,若OA=4 cm,则点A在☉O ;若OB=6 cm,则点B在☉O ;若OC=7 cm,则点C在☉O .
2.已知A为☉O外的一个点,且☉O的半径为9 cm,则线段OA的长度可能为 ( )
A.7 cm B.8 cm C.9 cm D.10 cm
3.如图1,边长为1的正方形ABCD的两条对角线相交于点O,以点A为圆心,1为半径画圆,则点O,B,C,D中,点 在圆内,点 在圆上,点 在圆外.
图1
4.[教材习题27.2第1题变式] 如图2,已知在△ABC中,AC=3,BC=4,∠C=90°,以点C为圆心作☉C,半径为r.
(1)当r在什么取值范围内时,点A,B都在☉C外
(2)当r在什么取值范围内时,点A在☉C内,点B在☉C外
图2
知识点 2 确定圆的条件
5.给定下列条件可以确定一个圆的是 ( )
A.已知圆心 B.已知半径
C.已知直径 D.已知不在同一直线上的三个点
6.如图3所示,点A,B,C在同一直线上,点M在直线AC外,经过图中的三个点作圆,可以作
个.
图3 图4
7.如图4所示,已知A,B,C三点(三点不在同一直线上),求作:☉O,使它经过A,B,C三点.(要求:尺规作图,不写作法,但要保留作图痕迹)
知识点 3 三角形的外接圆与圆的内接三角形
8.三角形的外心是三角形 的交点,其中直角三角形的外心是 的中点,锐角三角形的外心在三角形的 ,钝角三角形的外心在三角形的 .
9.如图5,若△ABC内接于半径为R的☉O,且∠A=60°,连结OB,OC,则边BC的长为 ( )
图5
A.R B.R C.R D.R
10.已知一个三角形的三边长分别为13 cm,12 cm,5 cm,则此三角形外接圆的半径为
cm.
11.如图6,在△ABC中,AB=AC.
(1)求作:△ABC的外接圆☉O(要求:尺规作图,保留作图痕迹,不写作法);
(2)若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则S☉O= .
图6
【能力提升】
12.如图7,在5×5的正方形网格中,每个小正方形的边长均为1,选取7个格点(小正方形的顶点),若以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个点在圆内,则r的取值范围是 ( )
图7
A.3
A.5 B.4 C.3 D.2
14.如图8所示,在Rt△ABC中,∠C=90°,∠A=30°,D为AB的中点,以点C为圆心,BC长为半径画圆,则点D与☉C的位置关系是 .
图8
15.如图9,△ABC内接于☉O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若☉O的半径为2,则CD的长为 .
图9
16.平面上有☉O及一点P,P到☉O上一点的距离最长为6 cm,最短为2 cm,则☉O的半径为 .
17.已知直线l:y=x-4,点A(1,0),点B(0,2),设P为直线l上一动点,当点P的坐标为 时,过P,A,B三点不能作出一个圆.
18.如图10,在矩形ABCD中,AB=3,AD=4.
(1)以点A为圆心,4为半径画☉A,并说出点B,C,D与☉A的位置关系;
(2)若以点A为圆心作☉A,且使点B,C,D中至少有一个点在☉A内,同时至少有一个点在☉A外,则☉A的半径r应满足什么条件
图10
19.如图11,在平面直角坐标系中,A(0,4),B(4,4),C(6,2).
(1)在图中画出经过A,B,C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 ;
(3)若DM=2,判断点D与☉M的位置关系.
图11
20.如图12,已知等腰直角三角形ABC,P是斜边BC上一点(不与点B,C重合),PE是△ABP的外接圆☉O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若☉O的直径为2,求PC2+PB2的值.
图12
27.2.1 点与圆的位置关系
1.内 上 外 2.D
3.O B,D C .
4.解:(1)当0
6.3
7.略
8.三条边的垂直平分线 斜边 内部 外部
9.D
10.6.5
11.解:(1)如图,☉O即为所求.
(2)25π
12.D .
13.B
14.点D在☉C上 .
15.
16.2 cm或4 cm
17.(2,-2)
18.解:(1)如图.∵AB=3<4,
∴点B在☉A内.
∵AD=4,∴点D在☉A上.
连结AC,由勾股定理可求出AC=5>4,
∴点C在☉A外.
(2)∵AB
(2)(2,0)
(3)☉M的半径AM==2.
∵DM=2,∴点D在☉M上.
20.解:(1)证明:∵△ABC是等腰直角三角形,BC是斜边,
∴∠C=∠ABC=45°,
∴∠AEP=∠ABP=45°.
∵PE是☉O的直径,
∴∠PAE=90°,
∴∠APE=∠AEP=45°,
∴AP=AE,
∴△APE是等腰直角三角形.
(2)∵∠CAB=∠PAE=90°,
∴∠CAP=∠BAE.
又∵AC=AB,AP=AE,
∴△CAP≌△BAE,
∴∠ACP=∠ABE=45°,PC=BE,
∴∠PBE=∠ABC+∠ABE=90°,
∴PC2+PB2=BE2+PB2=PE2=22=4.
