2021—2022学年华东师大版九年级数学下册27.2.3 第1课时 切线的判定与性质练习题(Word版含答案)
文档属性
| 名称 | 2021—2022学年华东师大版九年级数学下册27.2.3 第1课时 切线的判定与性质练习题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 236.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 10:50:14 | ||
图片预览

文档简介
27.2.3 第1课时 切线的判定与性质
知识点 1 切线的判定
1.下列直线中,一定是圆的切线的是 ( )
A.与圆有公共点的直线
B.垂直于圆的半径的直线
C.圆心到其距离等于半径的直线
D.经过圆心和直径的一端的直线
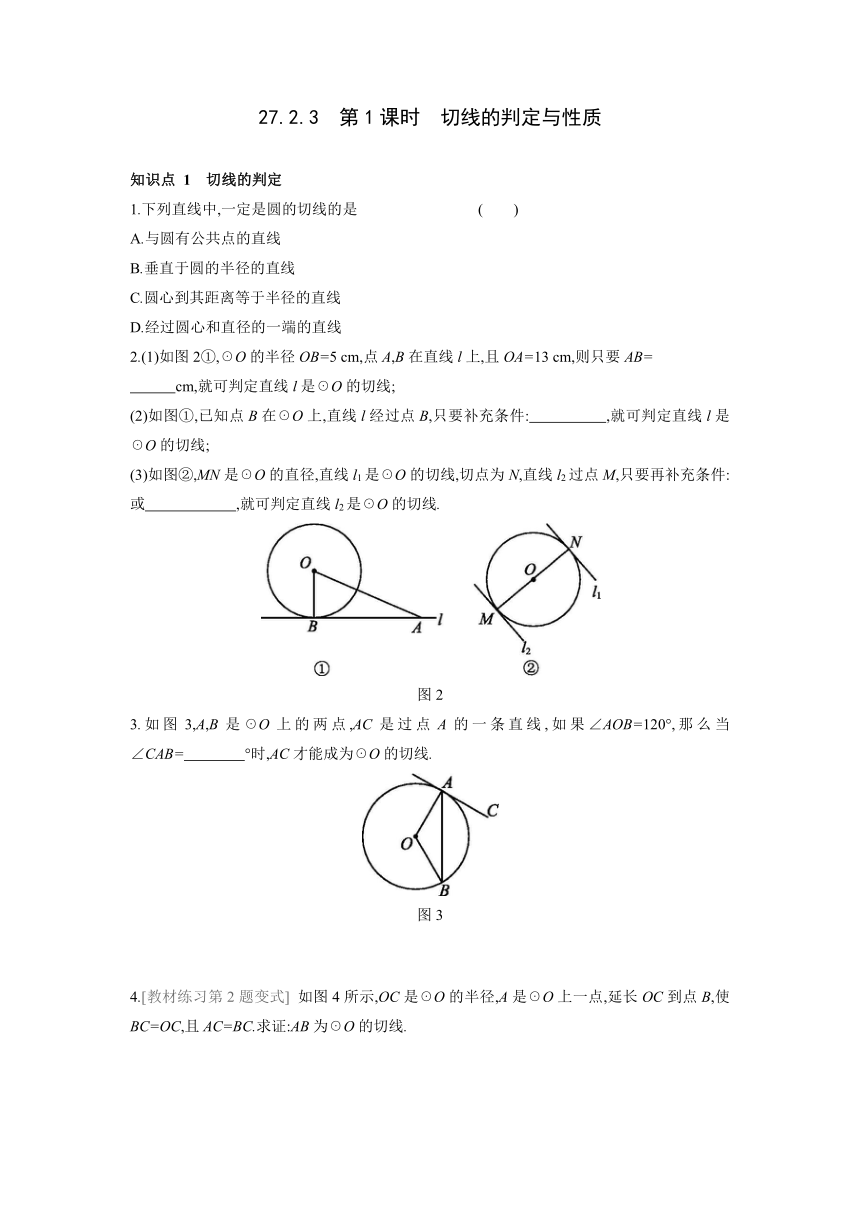
2.(1)如图2①,☉O的半径OB=5 cm,点A,B在直线l上,且OA=13 cm,则只要AB=
cm,就可判定直线l是☉O的切线;
(2)如图①,已知点B在☉O上,直线l经过点B,只要补充条件: ,就可判定直线l是☉O的切线;
(3)如图②,MN是☉O的直径,直线l1是☉O的切线,切点为N,直线l2过点M,只要再补充条件: 或 ,就可判定直线l2是☉O的切线.
图2
3.如图3,A,B是☉O上的两点,AC是过点A的一条直线,如果∠AOB=120°,那么当∠CAB= °时,AC才能成为☉O的切线.
图3
4.[教材练习第2题变式] 如图4所示,OC是☉O的半径,A是☉O上一点,延长OC到点B,使BC=OC,且AC=BC.求证:AB为☉O的切线.
图4
知识点 2 切线的性质
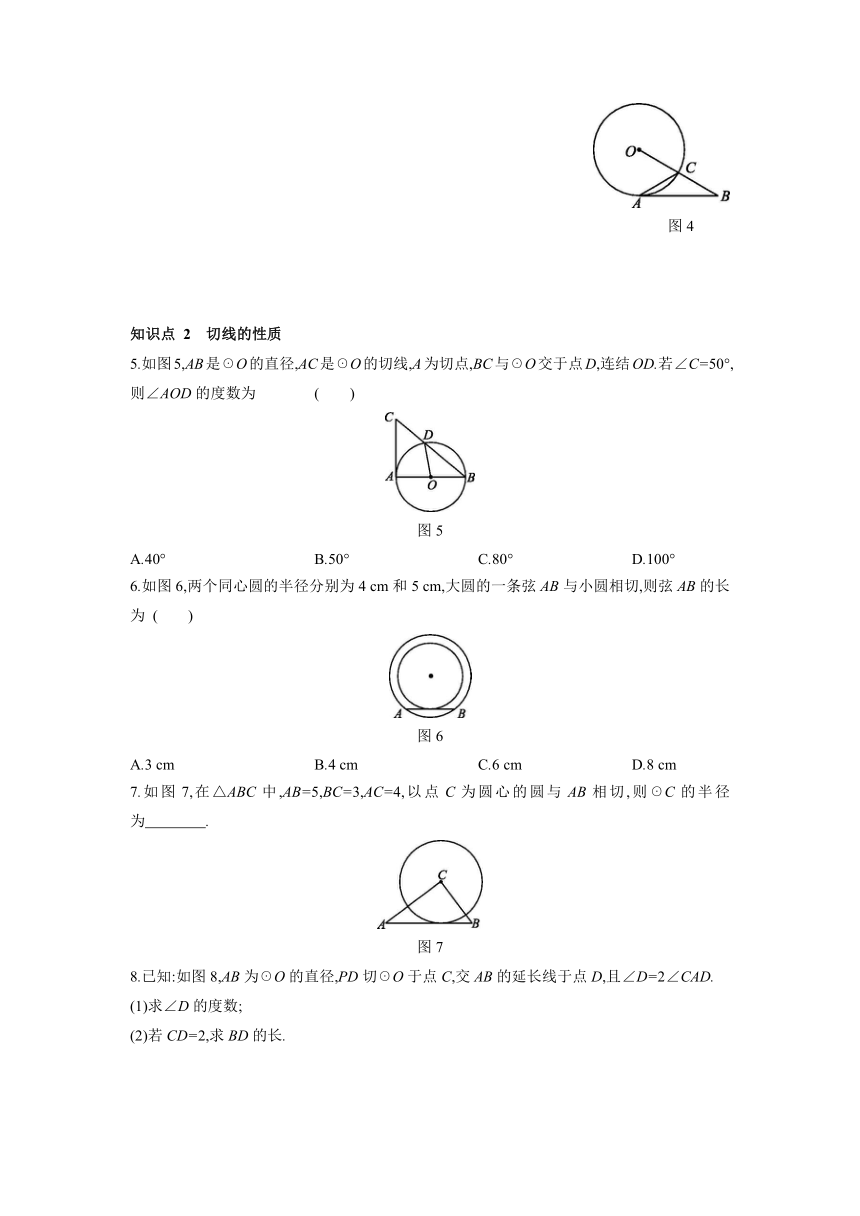
5.如图5,AB是☉O的直径,AC是☉O的切线,A为切点,BC与☉O交于点D,连结OD.若∠C=50°,则∠AOD的度数为 ( )
图5
A.40° B.50° C.80° D.100°
6.如图6,两个同心圆的半径分别为4 cm和5 cm,大圆的一条弦AB与小圆相切,则弦AB的长为 ( )
图6
A.3 cm B.4 cm C.6 cm D.8 cm
7.如图7,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则☉C的半径为 .
图7
8.已知:如图8,AB为☉O的直径,PD切☉O于点C,交AB的延长线于点D,且∠D=2∠CAD.
(1)求∠D的度数;
(2)若CD=2,求BD的长.
图8
【能力提升】
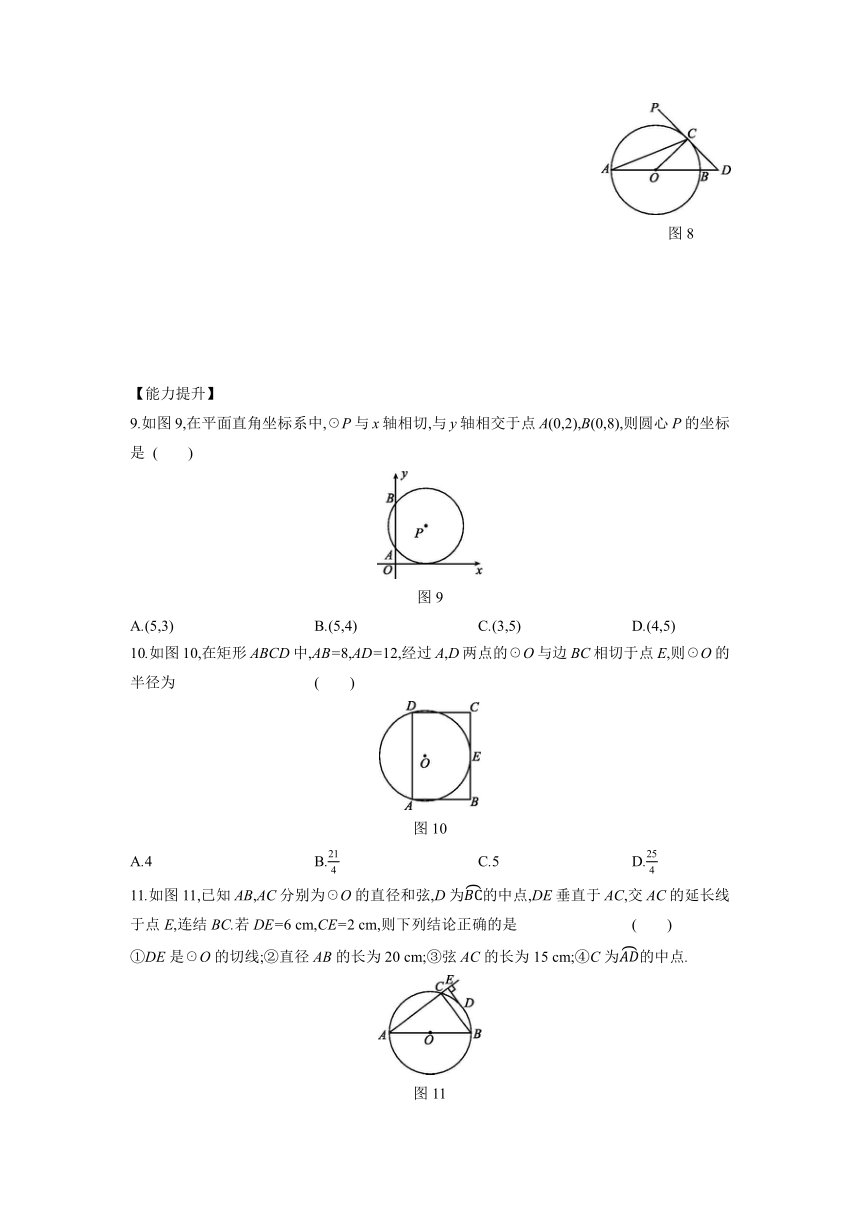
9.如图9,在平面直角坐标系中,☉P与x轴相切,与y轴相交于点A(0,2),B(0,8),则圆心P的坐标是 ( )
图9
A.(5,3) B.(5,4) C.(3,5) D.(4,5)
10.如图10,在矩形ABCD中,AB=8,AD=12,经过A,D两点的☉O与边BC相切于点E,则☉O的半径为 ( )
图10
A.4 B. C.5 D.
11.如图11,已知AB,AC分别为☉O的直径和弦,D为的中点,DE垂直于AC,交AC的延长线于点E,连结BC.若DE=6 cm,CE=2 cm,则下列结论正确的是 ( )
①DE是☉O的切线;②直径AB的长为20 cm;③弦AC的长为15 cm;④C为的中点.
图11
A.①②④ B.①③④ C.①② D.②③
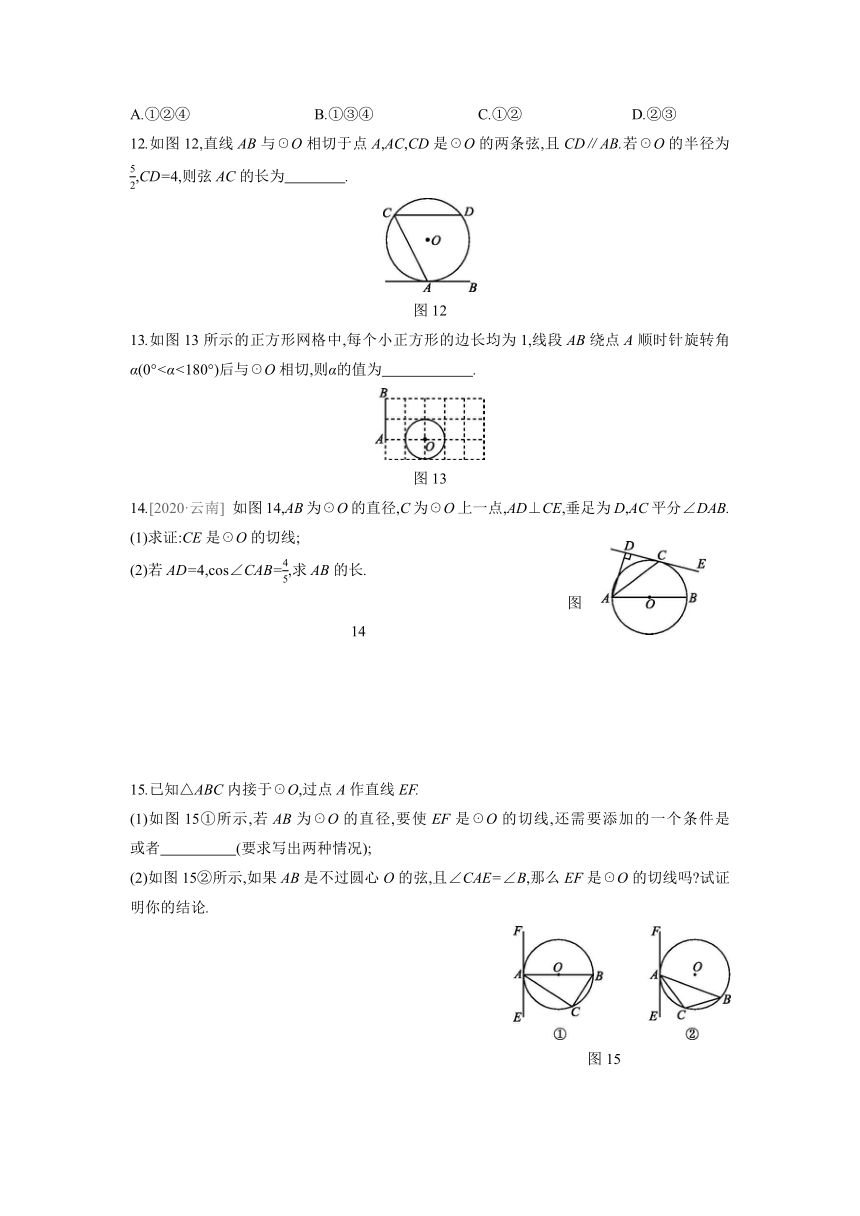
12.如图12,直线AB与☉O相切于点A,AC,CD是☉O的两条弦,且CD∥AB.若☉O的半径为,CD=4,则弦AC的长为 .
图12
13.如图13所示的正方形网格中,每个小正方形的边长均为1,线段AB绕点A顺时针旋转角α(0°<α<180°)后与☉O相切,则α的值为 .
图13
14.[2020·云南] 如图14,AB为☉O的直径,C为☉O上一点,AD⊥CE,垂足为D,AC平分∠DAB.
(1)求证:CE是☉O的切线;
(2)若AD=4,cos∠CAB=,求AB的长.
图14
15.已知△ABC内接于☉O,过点A作直线EF.
(1)如图15①所示,若AB为☉O的直径,要使EF是☉O的切线,还需要添加的一个条件是 或者 (要求写出两种情况);
(2)如图15②所示,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是☉O的切线吗 试证明你的结论.
图15
27.2.3 第1课时 切线的判定与性质
1.C
2.(1)12
(2)答案不唯一,如OB⊥l
(3)l1∥l2 l2⊥MN于点M
3.60
4.证明:连结OA.
∵BC=OC,AC=BC,∴OC=AC.
又∵OA=OC,
∴△OAC是等边三角形,
∴∠OAC=∠OCA=60°.
∵AC=BC,∠OCA=∠CAB+∠B,
∴∠CAB=30°,
∴∠OAB=∠OAC+∠CAB=90°.
∵A是☉O上一点,
∴AB为☉O的切线.
5.C
6.C [解析] 如图所示,
设圆心为O,切点为C,连结OA,OC,则OC⊥AB,
∴AC=BC.
在Rt△AOC中,OA=5 cm,OC=4 cm,根据勾股定理,得AC==3(cm),
∴AB=AC+BC=3+3=6(cm).故选C.
7.2.4 [解析] 在△ABC中,∵AB=5,BC=3,AC=4,∴AC2+BC2=32+42=52=AB2,
∴∠ACB=90°.如图,设切点为D,连结CD.∵AB是☉C的切线,
∴CD⊥AB,
∴S△ABC=AC·BC=AB·CD,
∴CD===2.4,∴☉C的半径为2.4.故答案为2.4.
8.解:(1)∵∠COD=2∠CAD,∠D=2∠CAD,
∴∠D=∠COD.
∵PD与☉O相切于点C,
∴OC⊥PD,即∠OCD=90°,
∴∠D=45°.
(2)由(1)知△OCD是等腰直角三角形,
∴OC=CD=2,即☉O的半径为2.
由勾股定理,得OD==2,
∴BD=OD-OB=2-2.
9.D [解析] 如图,过点P作PC⊥AB于点C,PD⊥x轴于点D,
连结PB.
∵P为圆心,
∴AC=BC.
∵A(0,2),B(0,8),
∴AB=8-2=6,
∴AC=BC=3,
∴OC=8-3=5.
∵☉P与x轴相切,
∴PD=PB=OC=5.
在Rt△PBC中,由勾股定理可得PC===4,
∴点P的坐标为(4,5).
10.D [解析] 如图,连结EO并延长交AD于点F,连结AO.∵☉O与BC边相切于点E,
∴OE⊥BC.∵四边形ABCD为矩形,∴BC∥AD,∴OF⊥AD,∴AF=DF=AD=6.
∵四边形ABCD为矩形,∴∠B=∠DAB=90°.又∵OE⊥BC,∴四边形ABEF为矩形,
∴EF=AB=8.设☉O的半径为r,则OA=r,OF=8-r.在Rt△AOF中,∵OF2+AF2=OA2,
∴(8-r)2+62=r2,解得r=.
故选D.
11.C [解析] 如图,连结OD,交BC于点F,连结OC,CD.
∵D为的中点,∴OD⊥BC,CF=BF.又∵AB为☉O的直径,DE⊥AE,∴∠BCE=∠DEC=
∠CFD=90°,∴四边形CEDF为矩形,∴OD⊥DE,∴DE为☉O的切线,故①正确.∴DF=CE=
2 cm,CF=DE=6 cm,∴BC=2CF=12 cm.设☉O的半径为r cm,则OF=(r-2)cm.在Rt△OCF中,由勾股定理可得OC2=OF2+CF2,即r2=(r-2)2+62,解得r=10,∴AB=20 cm,故②正确.
在Rt△ABC中,BC=12 cm,AB=20 cm,∴AC===16(cm),故③不正确.
若C为的中点,则AC=CD.在Rt△CDE中,CE=2 cm,DE=6 cm,
由勾股定理可得CD=2 cm≠AC,故④不正确.
综上可知正确的为①②.故选C.
12.2 [解析] 如图,连结AO并延长,交CD于点E,连结OC,易证OE⊥CD,
CE=DE=2.由勾股定理得OE=,故AE=4.由勾股定理得AC=2.
13.60°或120° [解析] 如图,线段AB绕点A顺时针旋转角α(0°<α<180°)后与☉O相切,设切点为C'和C″,连结OC',OC″,则OC'⊥AB',OC″⊥AB″.在Rt△OAC'中,∵OC'=1,OA=2,
∴∠OAC'=30°,∴∠BAB'=60°.同理可得∠OAC″=30°,∴∠BAB″=120°.
综上所述,α的值为60°或120°.故答案为60°或120°.
14.解:(1)证明:如图,连结OC.
∵OA=OC,
∴∠OAC=∠OCA.
∵AC平分∠DAB,
∴∠CAD=∠CAB,
∴∠CAD=∠OCA,
∴AD∥OC.
∵AD⊥DE,
∴OC⊥DE.
又∵OC是☉O的半径,
∴CE是☉O的切线.
(2)如图,连结BC.
∵AB为☉O的直径,
∴∠ACB=90°,
∴∠ADC=∠ACB.
∵AC平分∠DAB,
∴∠CAD=∠CAB,
∴cos∠CAD=cos∠CAB=,
∴在Rt△ACD中,AC=5,
∴在Rt△ABC中,cos∠CAB===,∴AB=.
15.解:(1)①∠BAE=90°,②∠EAC=∠ABC.
理由:①∵∠BAE=90°,∴AE⊥AB.
又∵AB是☉O的直径,
∴EF是☉O的切线.
②∵AB是☉O的直径,
∴∠ACB=90°,
∴∠ABC+∠BAC=90°.
∵∠EAC=∠ABC,
∴∠BAE=∠BAC+∠EAC=∠BAC+∠ABC=90°,
即AE⊥AB.
又∵AB是☉O的直径,∴EF是☉O的切线.
(2)EF是☉O的切线.
证明:如图,作直径AM,连结CM,
则∠ACM=90°,∠M=∠B,
∴∠M+∠CAM=∠B+∠CAM=90°.
∵∠CAE=∠B,
∴∠CAE+∠CAM=90°,
即AE⊥AM.
又∵AM是☉O的直径,
∴EF是☉O的切线.
知识点 1 切线的判定
1.下列直线中,一定是圆的切线的是 ( )
A.与圆有公共点的直线
B.垂直于圆的半径的直线
C.圆心到其距离等于半径的直线
D.经过圆心和直径的一端的直线
2.(1)如图2①,☉O的半径OB=5 cm,点A,B在直线l上,且OA=13 cm,则只要AB=
cm,就可判定直线l是☉O的切线;
(2)如图①,已知点B在☉O上,直线l经过点B,只要补充条件: ,就可判定直线l是☉O的切线;
(3)如图②,MN是☉O的直径,直线l1是☉O的切线,切点为N,直线l2过点M,只要再补充条件: 或 ,就可判定直线l2是☉O的切线.
图2
3.如图3,A,B是☉O上的两点,AC是过点A的一条直线,如果∠AOB=120°,那么当∠CAB= °时,AC才能成为☉O的切线.
图3
4.[教材练习第2题变式] 如图4所示,OC是☉O的半径,A是☉O上一点,延长OC到点B,使BC=OC,且AC=BC.求证:AB为☉O的切线.
图4
知识点 2 切线的性质
5.如图5,AB是☉O的直径,AC是☉O的切线,A为切点,BC与☉O交于点D,连结OD.若∠C=50°,则∠AOD的度数为 ( )
图5
A.40° B.50° C.80° D.100°
6.如图6,两个同心圆的半径分别为4 cm和5 cm,大圆的一条弦AB与小圆相切,则弦AB的长为 ( )
图6
A.3 cm B.4 cm C.6 cm D.8 cm
7.如图7,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则☉C的半径为 .
图7
8.已知:如图8,AB为☉O的直径,PD切☉O于点C,交AB的延长线于点D,且∠D=2∠CAD.
(1)求∠D的度数;
(2)若CD=2,求BD的长.
图8
【能力提升】
9.如图9,在平面直角坐标系中,☉P与x轴相切,与y轴相交于点A(0,2),B(0,8),则圆心P的坐标是 ( )
图9
A.(5,3) B.(5,4) C.(3,5) D.(4,5)
10.如图10,在矩形ABCD中,AB=8,AD=12,经过A,D两点的☉O与边BC相切于点E,则☉O的半径为 ( )
图10
A.4 B. C.5 D.
11.如图11,已知AB,AC分别为☉O的直径和弦,D为的中点,DE垂直于AC,交AC的延长线于点E,连结BC.若DE=6 cm,CE=2 cm,则下列结论正确的是 ( )
①DE是☉O的切线;②直径AB的长为20 cm;③弦AC的长为15 cm;④C为的中点.
图11
A.①②④ B.①③④ C.①② D.②③
12.如图12,直线AB与☉O相切于点A,AC,CD是☉O的两条弦,且CD∥AB.若☉O的半径为,CD=4,则弦AC的长为 .
图12
13.如图13所示的正方形网格中,每个小正方形的边长均为1,线段AB绕点A顺时针旋转角α(0°<α<180°)后与☉O相切,则α的值为 .
图13
14.[2020·云南] 如图14,AB为☉O的直径,C为☉O上一点,AD⊥CE,垂足为D,AC平分∠DAB.
(1)求证:CE是☉O的切线;
(2)若AD=4,cos∠CAB=,求AB的长.
图14
15.已知△ABC内接于☉O,过点A作直线EF.
(1)如图15①所示,若AB为☉O的直径,要使EF是☉O的切线,还需要添加的一个条件是 或者 (要求写出两种情况);
(2)如图15②所示,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是☉O的切线吗 试证明你的结论.
图15
27.2.3 第1课时 切线的判定与性质
1.C
2.(1)12
(2)答案不唯一,如OB⊥l
(3)l1∥l2 l2⊥MN于点M
3.60
4.证明:连结OA.
∵BC=OC,AC=BC,∴OC=AC.
又∵OA=OC,
∴△OAC是等边三角形,
∴∠OAC=∠OCA=60°.
∵AC=BC,∠OCA=∠CAB+∠B,
∴∠CAB=30°,
∴∠OAB=∠OAC+∠CAB=90°.
∵A是☉O上一点,
∴AB为☉O的切线.
5.C
6.C [解析] 如图所示,
设圆心为O,切点为C,连结OA,OC,则OC⊥AB,
∴AC=BC.
在Rt△AOC中,OA=5 cm,OC=4 cm,根据勾股定理,得AC==3(cm),
∴AB=AC+BC=3+3=6(cm).故选C.
7.2.4 [解析] 在△ABC中,∵AB=5,BC=3,AC=4,∴AC2+BC2=32+42=52=AB2,
∴∠ACB=90°.如图,设切点为D,连结CD.∵AB是☉C的切线,
∴CD⊥AB,
∴S△ABC=AC·BC=AB·CD,
∴CD===2.4,∴☉C的半径为2.4.故答案为2.4.
8.解:(1)∵∠COD=2∠CAD,∠D=2∠CAD,
∴∠D=∠COD.
∵PD与☉O相切于点C,
∴OC⊥PD,即∠OCD=90°,
∴∠D=45°.
(2)由(1)知△OCD是等腰直角三角形,
∴OC=CD=2,即☉O的半径为2.
由勾股定理,得OD==2,
∴BD=OD-OB=2-2.
9.D [解析] 如图,过点P作PC⊥AB于点C,PD⊥x轴于点D,
连结PB.
∵P为圆心,
∴AC=BC.
∵A(0,2),B(0,8),
∴AB=8-2=6,
∴AC=BC=3,
∴OC=8-3=5.
∵☉P与x轴相切,
∴PD=PB=OC=5.
在Rt△PBC中,由勾股定理可得PC===4,
∴点P的坐标为(4,5).
10.D [解析] 如图,连结EO并延长交AD于点F,连结AO.∵☉O与BC边相切于点E,
∴OE⊥BC.∵四边形ABCD为矩形,∴BC∥AD,∴OF⊥AD,∴AF=DF=AD=6.
∵四边形ABCD为矩形,∴∠B=∠DAB=90°.又∵OE⊥BC,∴四边形ABEF为矩形,
∴EF=AB=8.设☉O的半径为r,则OA=r,OF=8-r.在Rt△AOF中,∵OF2+AF2=OA2,
∴(8-r)2+62=r2,解得r=.
故选D.
11.C [解析] 如图,连结OD,交BC于点F,连结OC,CD.
∵D为的中点,∴OD⊥BC,CF=BF.又∵AB为☉O的直径,DE⊥AE,∴∠BCE=∠DEC=
∠CFD=90°,∴四边形CEDF为矩形,∴OD⊥DE,∴DE为☉O的切线,故①正确.∴DF=CE=
2 cm,CF=DE=6 cm,∴BC=2CF=12 cm.设☉O的半径为r cm,则OF=(r-2)cm.在Rt△OCF中,由勾股定理可得OC2=OF2+CF2,即r2=(r-2)2+62,解得r=10,∴AB=20 cm,故②正确.
在Rt△ABC中,BC=12 cm,AB=20 cm,∴AC===16(cm),故③不正确.
若C为的中点,则AC=CD.在Rt△CDE中,CE=2 cm,DE=6 cm,
由勾股定理可得CD=2 cm≠AC,故④不正确.
综上可知正确的为①②.故选C.
12.2 [解析] 如图,连结AO并延长,交CD于点E,连结OC,易证OE⊥CD,
CE=DE=2.由勾股定理得OE=,故AE=4.由勾股定理得AC=2.
13.60°或120° [解析] 如图,线段AB绕点A顺时针旋转角α(0°<α<180°)后与☉O相切,设切点为C'和C″,连结OC',OC″,则OC'⊥AB',OC″⊥AB″.在Rt△OAC'中,∵OC'=1,OA=2,
∴∠OAC'=30°,∴∠BAB'=60°.同理可得∠OAC″=30°,∴∠BAB″=120°.
综上所述,α的值为60°或120°.故答案为60°或120°.
14.解:(1)证明:如图,连结OC.
∵OA=OC,
∴∠OAC=∠OCA.
∵AC平分∠DAB,
∴∠CAD=∠CAB,
∴∠CAD=∠OCA,
∴AD∥OC.
∵AD⊥DE,
∴OC⊥DE.
又∵OC是☉O的半径,
∴CE是☉O的切线.
(2)如图,连结BC.
∵AB为☉O的直径,
∴∠ACB=90°,
∴∠ADC=∠ACB.
∵AC平分∠DAB,
∴∠CAD=∠CAB,
∴cos∠CAD=cos∠CAB=,
∴在Rt△ACD中,AC=5,
∴在Rt△ABC中,cos∠CAB===,∴AB=.
15.解:(1)①∠BAE=90°,②∠EAC=∠ABC.
理由:①∵∠BAE=90°,∴AE⊥AB.
又∵AB是☉O的直径,
∴EF是☉O的切线.
②∵AB是☉O的直径,
∴∠ACB=90°,
∴∠ABC+∠BAC=90°.
∵∠EAC=∠ABC,
∴∠BAE=∠BAC+∠EAC=∠BAC+∠ABC=90°,
即AE⊥AB.
又∵AB是☉O的直径,∴EF是☉O的切线.
(2)EF是☉O的切线.
证明:如图,作直径AM,连结CM,
则∠ACM=90°,∠M=∠B,
∴∠M+∠CAM=∠B+∠CAM=90°.
∵∠CAE=∠B,
∴∠CAE+∠CAM=90°,
即AE⊥AM.
又∵AM是☉O的直径,
∴EF是☉O的切线.
