2021—2022学年华东师大版九年级数学下册27.2.3 第2课时 切线长定理及三角形的内切圆 练习题(Word版含答案)
文档属性
| 名称 | 2021—2022学年华东师大版九年级数学下册27.2.3 第2课时 切线长定理及三角形的内切圆 练习题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 161.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 00:00:00 | ||
图片预览


文档简介
27.2.3第2课时 切线长定理及三角形的内切圆
知识点 1 切线长定理
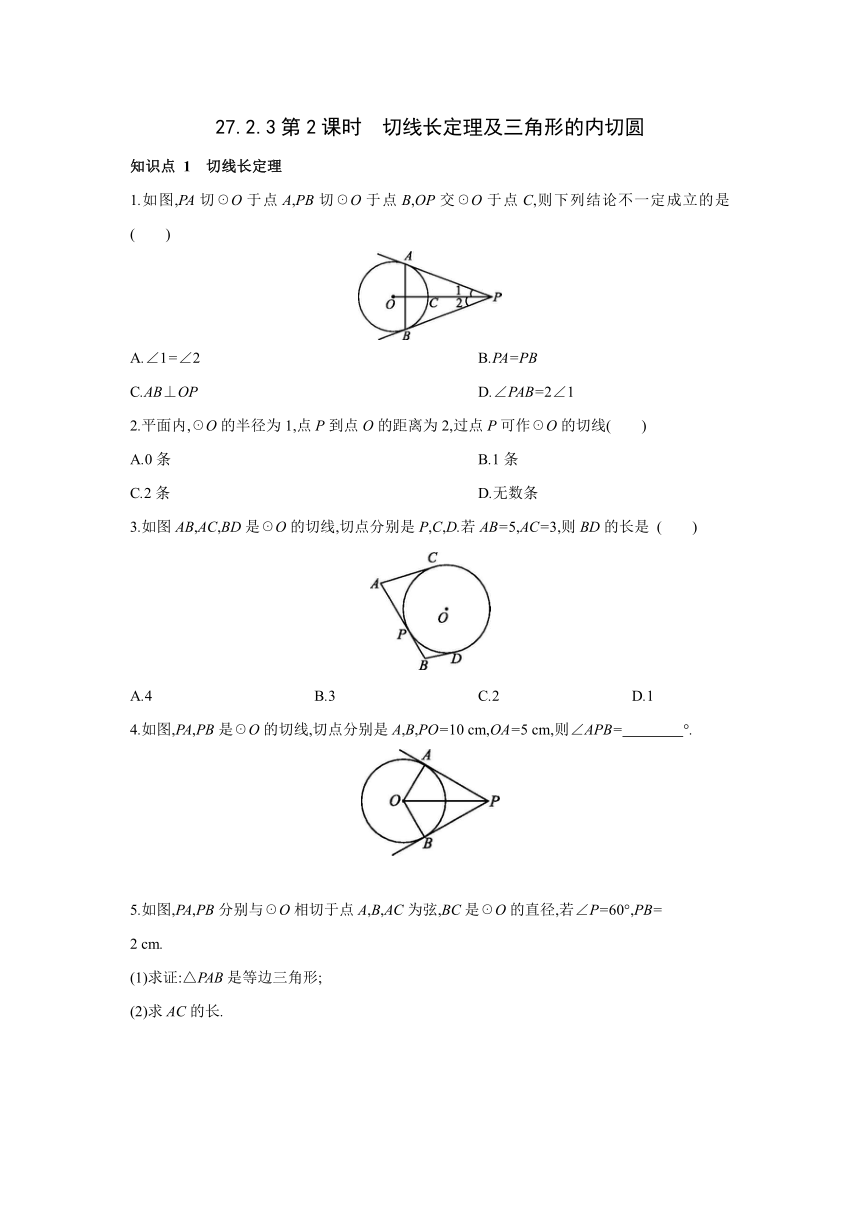
1.如图,PA切☉O于点A,PB切☉O于点B,OP交☉O于点C,则下列结论不一定成立的是 ( )
A.∠1=∠2 B.PA=PB
C.AB⊥OP D.∠PAB=2∠1
2.平面内,☉O的半径为1,点P到点O的距离为2,过点P可作☉O的切线( )
A.0条 B.1条
C.2条 D.无数条
3.如图AB,AC,BD是☉O的切线,切点分别是P,C,D.若AB=5,AC=3,则BD的长是 ( )
A.4 B.3 C.2 D.1
4.如图,PA,PB是☉O的切线,切点分别是A,B,PO=10 cm,OA=5 cm,则∠APB= °.
5.如图,PA,PB分别与☉O相切于点A,B,AC为弦,BC是☉O的直径,若∠P=60°,PB=
2 cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
知识点 2 三角形的内切圆及圆的外切三角形
6.下列关于三角形的内心的说法正确的是 ( )
A.内心是三角形三条角平分线的交点
B.内心是三角形三条边的垂直平分线的交点
C.内心到三角形三个顶点的距离相等
D.钝角三角形的内心在三角形外部
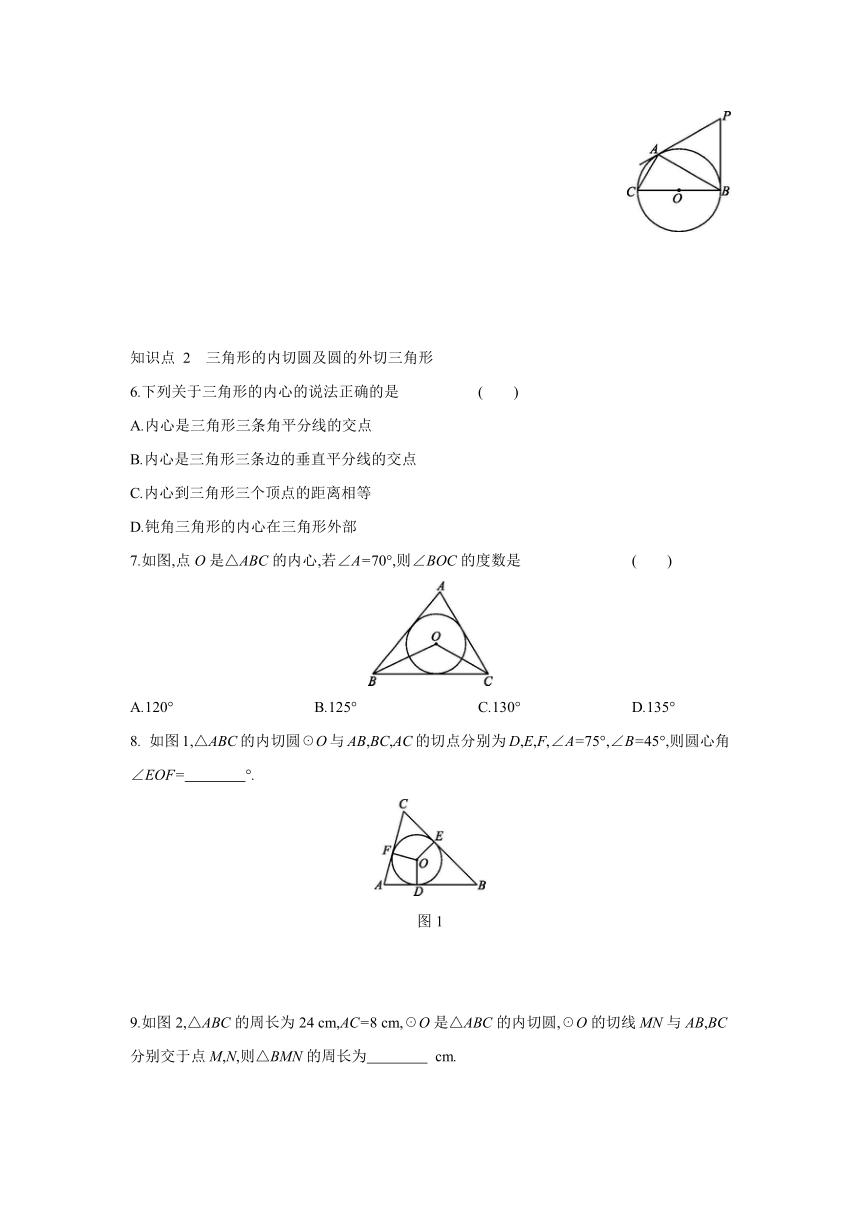
7.如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是 ( )
A.120° B.125° C.130° D.135°
8. 如图1,△ABC的内切圆☉O与AB,BC,AC的切点分别为D,E,F,∠A=75°,∠B=45°,则圆心角∠EOF= °.
图1
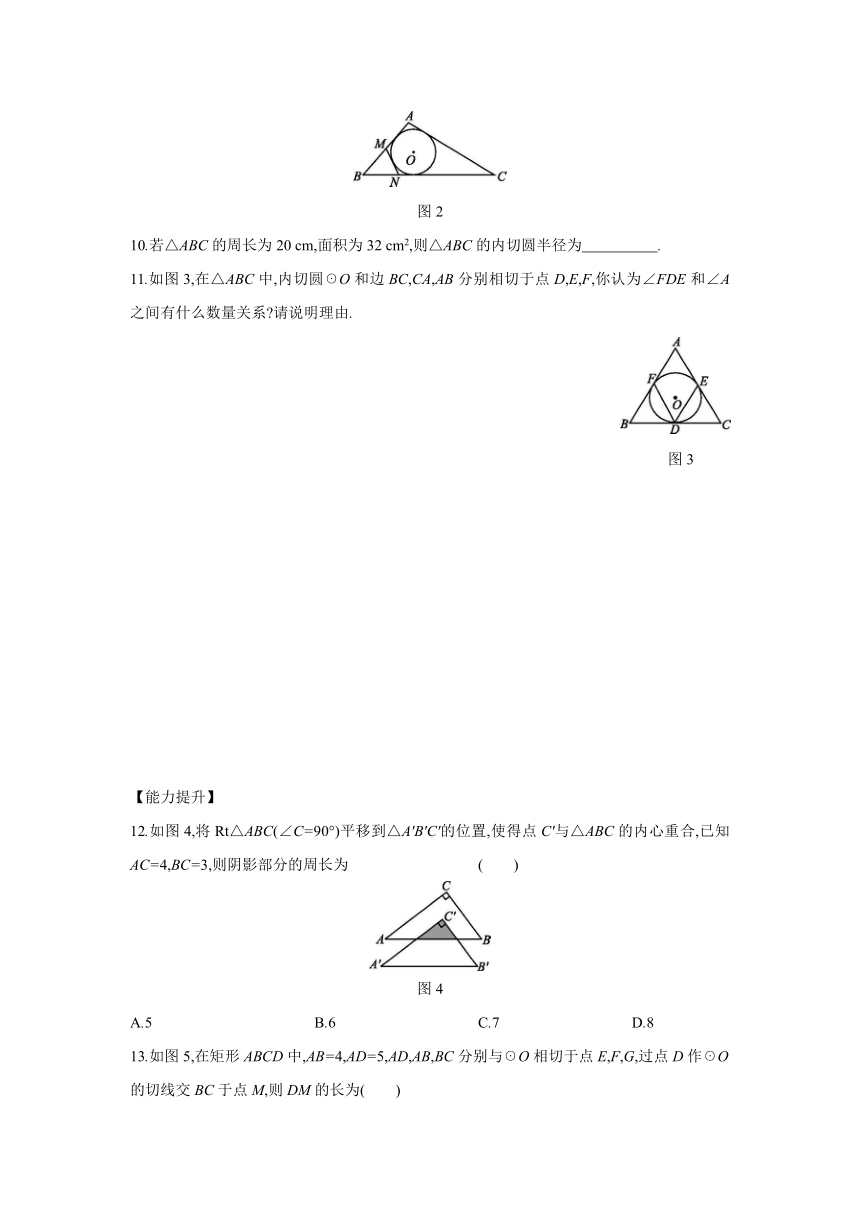
9.如图2,△ABC的周长为24 cm,AC=8 cm,☉O是△ABC的内切圆,☉O的切线MN与AB,BC分别交于点M,N,则△BMN的周长为 cm.
图2
10.若△ABC的周长为20 cm,面积为32 cm2,则△ABC的内切圆半径为 .
11.如图3,在△ABC中,内切圆☉O和边BC,CA,AB分别相切于点D,E,F,你认为∠FDE和∠A之间有什么数量关系 请说明理由.
图3
【能力提升】
12.如图4,将Rt△ABC(∠C=90°)平移到△A'B'C'的位置,使得点C'与△ABC的内心重合,已知AC=4,BC=3,则阴影部分的周长为 ( )
图4
A.5 B.6 C.7 D.8
13.如图5,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与☉O相切于点E,F,G,过点D作☉O的切线交BC于点M,则DM的长为( )
图5
A. B. C. D.2
14.如图6,PA,PB是☉O的两条切线,A,B为切点,直线OP交☉O于点D,E,交AB于点C.
图6
(1)图中的垂直关系有: ;
(2)图中的全等三角形有: ;
(3)若PA=4 cm,PD=2 cm,则半径OA的长为 .
15.如图7,AB,BC,CD分别与☉O相切于点E,F,G,且AB∥CD,连结OB,OC,延长CO交☉O于点M,过点M作MN∥OB交CD于点N.
(1)求证:MN是☉O的切线;
(2)当OB=6 cm,OC=8 cm时,求☉O的半径及MN的长.
图7
答案
1.D 2.C 3.C
4.60 [解析] 因为PA,PB是☉O的切线,所以∠OAP=∠OBP=90°,∠APO=∠BPO,所以
sin∠APO==,所以∠APO=30°,所以∠APB=60°.
5.解:(1)证明:∵PA,PB分别与☉O相切于点A,B,
∴PA=PB.
又∵∠P=60°,
∴△PAB是等边三角形.
(2)∵△PAB是等边三角形,
∴AB=PB=2 cm,∠PBA=60°.
∵BC是☉O的直径,PB是☉O的切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC==,
∴AC=AB=(cm).
6.A
7.B [解析] ∵O是△ABC的内心,∴BO平分∠ABC,CO平分∠ACB,∴∠OBC=∠ABC,
∠OCB=∠ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=×(180°-70°)=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.故选B.
8.120
9.8 [解析] 设☉O与△ABC的各边的切点分别为D,E,F,☉O与MN相切于点G,如图,
∴AD=AF,BD=BE,CF=CE.
∵AC=8,即AF+CF=8,
∴AD+CE=8.
∵△ABC的周长为24,
∴AB+BC+AC=24,
∴AB+BC=16,
即BD+AD+BE+CE=16,
∴BD+BE=8.
∵☉O的切线MN与AB,BC分别交于点M,N,
∴MD=MG,NG=NE,
∴△BMN的周长=BM+BN+MN=BM+BN+MG+NG=BM+BN+MD+NE=BD+BE=8(cm).
10.3.2 cm
11.解:∠A=180°-2∠FDE.
理由:连结OE,OF,则OE⊥AC,OF⊥AB,
∴∠OEA=∠OFA=90°,
∴∠EOF+∠A=180°,
即∠A=180°-∠EOF.
又∵∠EOF=2∠FDE,
∴∠A=180°-2∠FDE.
12.A [解析] 连结AC',BC',设A'C',B'C'分别交AB于点D,E,如图.
∵在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB==5.
∵将Rt△ABC平移到△A'B'C'的位置,
∴AC∥A'C',BC∥B'C',
∴∠CAC'=∠DC'A,∠CBC'=∠BC'E.
∵点C'为△ABC的内心,
∴∠CAC'=∠DAC',∠CBC'=∠EBC',
∴∠DC'A=∠DAC',∠BC'E=∠EBC',
∴DC'=DA,EB=EC',
∴阴影部分的周长=DC'+DE+EC'=DA+DE+EB=AB=5.故选A.
13.A [解析] 设DM与☉O相切于点N.由题意,易知AE=AF=BF=BG=2,则CG=DE=DN=3.设GM=x,则MN=x,CM=3-x,DM=3+x.由勾股定理,得DM2=DC2+CM2,即(3+x)2=42+(3-x)2,解得x=,所以DM=.
14.(1)OA⊥PA,OB⊥PB,OP⊥AB
(2)△OAP≌△OBP,△OCA≌△OCB,△ACP≌△BCP
(3)3 cm [解析] 设OA=x cm.
在Rt△OAP中,由勾股定理,得AP2+OA2=OP2,即42+x2=(x+2)2,
解得x=3,∴半径OA的长为3 cm.
15.解:(1)证明:∵AB,BC,CD分别与☉O相切于点E,F,G,
∴∠OBC=∠ABC,∠OCB=∠DCB.
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°=90°,
∴∠BOM=90°.
∵MN∥OB,
∴∠NMC=∠BOM=90°,
即MN⊥MC.
又∵MO是☉O的半径,
∴MN是☉O的切线.
(2)如图,连结OF,则OF⊥BC.
由(1)知,△BOC是直角三角形,
∴BC===10(cm).
∵S△BOC=OB·OC=BC·OF,
∴×6×8=×10·OF,∴OF=4.8 cm,
∴☉O的半径为4.8 cm.
由(1)知,∠NCM=∠BCO,∠NMC=∠BOC=90°,
∴△NMC∽△BOC,
∴=,即=,
∴MN=9.6(cm).
知识点 1 切线长定理
1.如图,PA切☉O于点A,PB切☉O于点B,OP交☉O于点C,则下列结论不一定成立的是 ( )
A.∠1=∠2 B.PA=PB
C.AB⊥OP D.∠PAB=2∠1
2.平面内,☉O的半径为1,点P到点O的距离为2,过点P可作☉O的切线( )
A.0条 B.1条
C.2条 D.无数条
3.如图AB,AC,BD是☉O的切线,切点分别是P,C,D.若AB=5,AC=3,则BD的长是 ( )
A.4 B.3 C.2 D.1
4.如图,PA,PB是☉O的切线,切点分别是A,B,PO=10 cm,OA=5 cm,则∠APB= °.
5.如图,PA,PB分别与☉O相切于点A,B,AC为弦,BC是☉O的直径,若∠P=60°,PB=
2 cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
知识点 2 三角形的内切圆及圆的外切三角形
6.下列关于三角形的内心的说法正确的是 ( )
A.内心是三角形三条角平分线的交点
B.内心是三角形三条边的垂直平分线的交点
C.内心到三角形三个顶点的距离相等
D.钝角三角形的内心在三角形外部
7.如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是 ( )
A.120° B.125° C.130° D.135°
8. 如图1,△ABC的内切圆☉O与AB,BC,AC的切点分别为D,E,F,∠A=75°,∠B=45°,则圆心角∠EOF= °.
图1
9.如图2,△ABC的周长为24 cm,AC=8 cm,☉O是△ABC的内切圆,☉O的切线MN与AB,BC分别交于点M,N,则△BMN的周长为 cm.
图2
10.若△ABC的周长为20 cm,面积为32 cm2,则△ABC的内切圆半径为 .
11.如图3,在△ABC中,内切圆☉O和边BC,CA,AB分别相切于点D,E,F,你认为∠FDE和∠A之间有什么数量关系 请说明理由.
图3
【能力提升】
12.如图4,将Rt△ABC(∠C=90°)平移到△A'B'C'的位置,使得点C'与△ABC的内心重合,已知AC=4,BC=3,则阴影部分的周长为 ( )
图4
A.5 B.6 C.7 D.8
13.如图5,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与☉O相切于点E,F,G,过点D作☉O的切线交BC于点M,则DM的长为( )
图5
A. B. C. D.2
14.如图6,PA,PB是☉O的两条切线,A,B为切点,直线OP交☉O于点D,E,交AB于点C.
图6
(1)图中的垂直关系有: ;
(2)图中的全等三角形有: ;
(3)若PA=4 cm,PD=2 cm,则半径OA的长为 .
15.如图7,AB,BC,CD分别与☉O相切于点E,F,G,且AB∥CD,连结OB,OC,延长CO交☉O于点M,过点M作MN∥OB交CD于点N.
(1)求证:MN是☉O的切线;
(2)当OB=6 cm,OC=8 cm时,求☉O的半径及MN的长.
图7
答案
1.D 2.C 3.C
4.60 [解析] 因为PA,PB是☉O的切线,所以∠OAP=∠OBP=90°,∠APO=∠BPO,所以
sin∠APO==,所以∠APO=30°,所以∠APB=60°.
5.解:(1)证明:∵PA,PB分别与☉O相切于点A,B,
∴PA=PB.
又∵∠P=60°,
∴△PAB是等边三角形.
(2)∵△PAB是等边三角形,
∴AB=PB=2 cm,∠PBA=60°.
∵BC是☉O的直径,PB是☉O的切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC==,
∴AC=AB=(cm).
6.A
7.B [解析] ∵O是△ABC的内心,∴BO平分∠ABC,CO平分∠ACB,∴∠OBC=∠ABC,
∠OCB=∠ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=×(180°-70°)=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.故选B.
8.120
9.8 [解析] 设☉O与△ABC的各边的切点分别为D,E,F,☉O与MN相切于点G,如图,
∴AD=AF,BD=BE,CF=CE.
∵AC=8,即AF+CF=8,
∴AD+CE=8.
∵△ABC的周长为24,
∴AB+BC+AC=24,
∴AB+BC=16,
即BD+AD+BE+CE=16,
∴BD+BE=8.
∵☉O的切线MN与AB,BC分别交于点M,N,
∴MD=MG,NG=NE,
∴△BMN的周长=BM+BN+MN=BM+BN+MG+NG=BM+BN+MD+NE=BD+BE=8(cm).
10.3.2 cm
11.解:∠A=180°-2∠FDE.
理由:连结OE,OF,则OE⊥AC,OF⊥AB,
∴∠OEA=∠OFA=90°,
∴∠EOF+∠A=180°,
即∠A=180°-∠EOF.
又∵∠EOF=2∠FDE,
∴∠A=180°-2∠FDE.
12.A [解析] 连结AC',BC',设A'C',B'C'分别交AB于点D,E,如图.
∵在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB==5.
∵将Rt△ABC平移到△A'B'C'的位置,
∴AC∥A'C',BC∥B'C',
∴∠CAC'=∠DC'A,∠CBC'=∠BC'E.
∵点C'为△ABC的内心,
∴∠CAC'=∠DAC',∠CBC'=∠EBC',
∴∠DC'A=∠DAC',∠BC'E=∠EBC',
∴DC'=DA,EB=EC',
∴阴影部分的周长=DC'+DE+EC'=DA+DE+EB=AB=5.故选A.
13.A [解析] 设DM与☉O相切于点N.由题意,易知AE=AF=BF=BG=2,则CG=DE=DN=3.设GM=x,则MN=x,CM=3-x,DM=3+x.由勾股定理,得DM2=DC2+CM2,即(3+x)2=42+(3-x)2,解得x=,所以DM=.
14.(1)OA⊥PA,OB⊥PB,OP⊥AB
(2)△OAP≌△OBP,△OCA≌△OCB,△ACP≌△BCP
(3)3 cm [解析] 设OA=x cm.
在Rt△OAP中,由勾股定理,得AP2+OA2=OP2,即42+x2=(x+2)2,
解得x=3,∴半径OA的长为3 cm.
15.解:(1)证明:∵AB,BC,CD分别与☉O相切于点E,F,G,
∴∠OBC=∠ABC,∠OCB=∠DCB.
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠OBC+∠OCB=(∠ABC+∠DCB)=×180°=90°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°=90°,
∴∠BOM=90°.
∵MN∥OB,
∴∠NMC=∠BOM=90°,
即MN⊥MC.
又∵MO是☉O的半径,
∴MN是☉O的切线.
(2)如图,连结OF,则OF⊥BC.
由(1)知,△BOC是直角三角形,
∴BC===10(cm).
∵S△BOC=OB·OC=BC·OF,
∴×6×8=×10·OF,∴OF=4.8 cm,
∴☉O的半径为4.8 cm.
由(1)知,∠NCM=∠BCO,∠NMC=∠BOC=90°,
∴△NMC∽△BOC,
∴=,即=,
∴MN=9.6(cm).
