2021—2022学年华东师大版九年级数学下册27.3 第1课时 弧长和扇形的面积 练习题(Word版含答案)
文档属性
| 名称 | 2021—2022学年华东师大版九年级数学下册27.3 第1课时 弧长和扇形的面积 练习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 154.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 10:55:34 | ||
图片预览



文档简介
27.3 第1课时 弧长和扇形的面积
知识点 1 弧长公式及其应用
1.在半径为R的圆中,1°的圆心角所对的弧长l= ,n°的圆心角所对的弧长l= .
2.若扇形的圆心角为90°,半径为6,则该扇形的弧长为 ( )
A.π B.2π C.3π D.6π
3.如图1,AB是☉O的直径,D为☉O上一点,且∠ABD=30°,BO=4,则的长为 ( )
图1
A.π B.π C.2π D.π
4.已知扇形的圆心角为120°,弧长为2π,则它的半径为 .
5.[2020·金华] 如图2,的半径OA=2,OC⊥AB于点C,∠AOC=60°.
(1)求弦AB的长;
(2)求的长.
图2
知识点 2 扇形的面积公式及其应用
6.若一个扇形的圆心角为90°,半径为6,则该扇形的面积为 ( )
A. B.3π C.6π D.9π
7.如图3,在 ABCD中,∠B=60°,☉C的半径为3,则图中阴影部分的面积是 ( )
图3
A.π B.2π C.3π D.6π
8.钟面上分针的长为1,从上午9点到上午9点30分,分针在钟面上扫过的面积是 ( )
A.π B.π C.π D.π
9.如图4所示,分别以△ABC的三个顶点为圆心作☉A,☉B,☉C,且半径都是0.5 cm(三个圆两两不相交),则图中阴影部分的面积等于 ( )
图4
A. cm2 B. cm2 C. cm2 D. cm2
10.如图5,在矩形ABCD中,AB=4,AD=2,分别以点A,C为圆心,AD,CB长为半径画弧,交AB于点E,交CD于点F,则图中阴影部分的面积是 ( )
图5
A.4-2π B.8- C.8-2π D.8-4π
11.若一个扇形的面积为4π,它所对的圆心角为90°,则这个扇形的半径为 .
12.已知扇形的面积为2π,半径为3,则该扇形的弧长为 .(结果保留π)
13. 已知图6中扇形的半径为6厘米,求下列扇形的面积和周长.(π取3.14)
图6
【综合练习】
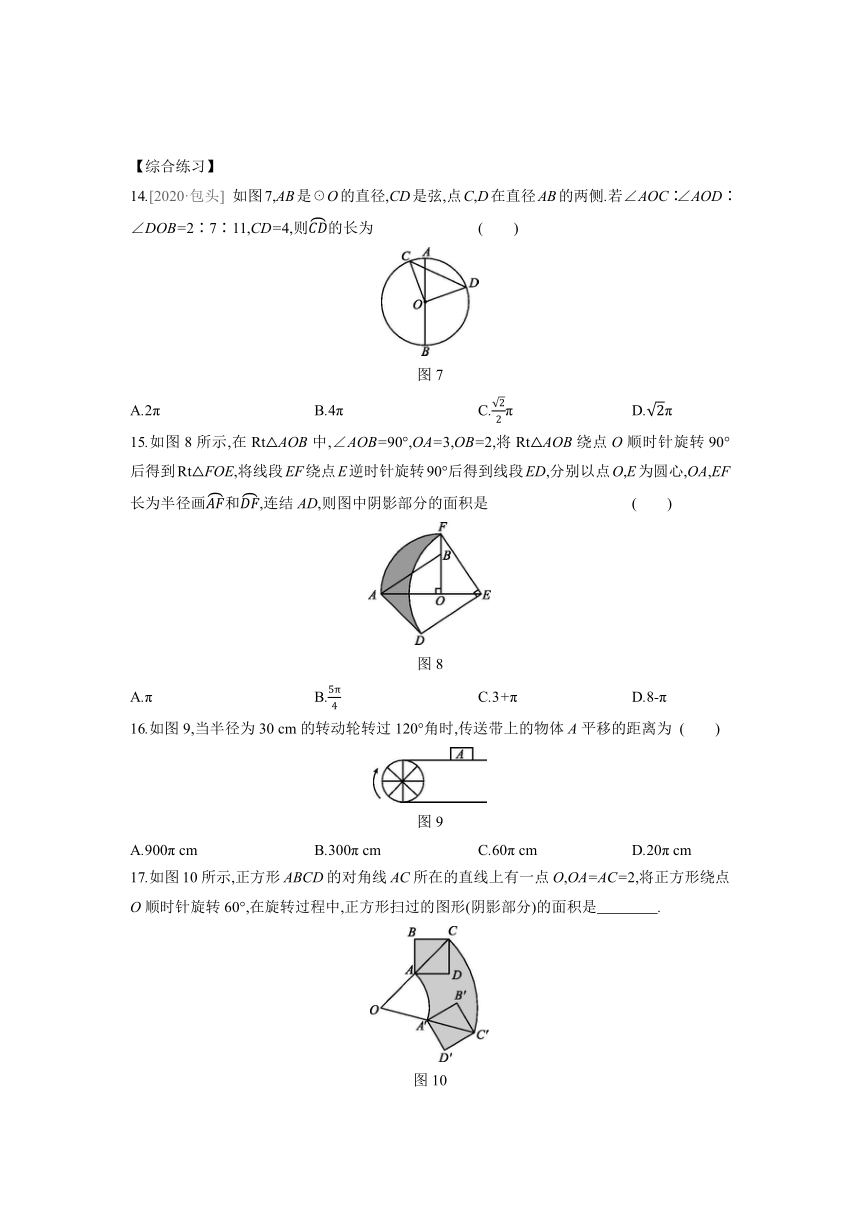
14.[2020·包头] 如图7,AB是☉O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC∶∠AOD∶∠DOB=2∶7∶11,CD=4,则的长为 ( )
图7
A.2π B.4π C.π D.π
15.如图8所示,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得到Rt△FOE,将线段EF绕点E逆时针旋转90°后得到线段ED,分别以点O,E为圆心,OA,EF长为半径画和,连结AD,则图中阴影部分的面积是 ( )
图8
A.π B. C.3+π D.8-π
16.如图9,当半径为30 cm的转动轮转过120°角时,传送带上的物体A平移的距离为 ( )
图9
A.900π cm B.300π cm C.60π cm D.20π cm
17.如图10所示,正方形ABCD的对角线AC所在的直线上有一点O,OA=AC=2,将正方形绕点O顺时针旋转60°,在旋转过程中,正方形扫过的图形(阴影部分)的面积是 .
图10
18.如图11所示,点D在半圆O的直径AB的延长线上,点C在半圆O上,AC=CD,
∠ACD=120°.
(1)求证:CD是半圆O的切线;
(2)若半圆O的半径为2,求图中阴影部分的面积.
图11
19.如图12,已知AB为☉O的直径,CD是弦,AB⊥CD于点E,OF⊥AC于点F,BE=OF.
(1)求证:OF∥BC;
(2)求证:△AFO≌△CEB;
(3)若EB=5 cm,CD=10 cm,设OE=x cm,求x的值及图中阴影部分的面积.
图12
27.3 第1课时 弧长和扇形的面积
1.
2.C [解析] 该扇形的弧长==3π.故选C.
3.D [解析] 如图,连结OD.
∵∠ABD=30°,
∴∠AOD=2∠ABD=60°,
∴∠BOD=120°,
∴的长==.
故选D.
4.3
5.解:(1)∵的半径OA=2,OC⊥AB于点C,∠AOC=60°,
∴AC=OA·sin60°=2×=,
∴AB=2AC=2.
(2)∵OA=OB,OC⊥AB,∠AOC=60°,
∴∠AOB=120°.
∵OA=2,
∴的长是=.
6.D
7.C [解析] ∵在 ABCD中,∠B=60°,
∴∠C=120°,
∴图中阴影部分的面积是=3π.
故选C.
8.A [解析] 钟面上分针的长为1,即R=1.从上午9点到上午9点30分,分针在钟面上绕着轴心旋转了180°,即n=180,所以S扇形===π.故选A.
9.B
10.C [解析] ∵矩形ABCD的面积为8,两个全等扇形面积之和为×π×22=2π,
∴阴影部分的面积为8-2π.
故选C.
11.4 [解析] ∵S=,
∴r2==16,
∴r=4.
12. [解析] 设扇形的弧长为l,则l×3=2π,解得l=.
13.[解析] (1)依据S=lr求面积.
(2)扇形的面积=×πr2,由此代入数据即可解决问题;扇形的周长=半径的长度×2+圆的周长×,据此代入数据即可求解.
解:(1)面积:×15.7×6=47.1(厘米2);
周长:6×2+15.7=12+15.7=27.7(厘米).
答:这个扇形的面积是47.1平方厘米,周长是27.7厘米.
(2)面积:×π×62≈×3.14×36=18.84(厘米2);
周长:6×2+π×6×2×≈12+6.28=18.28(厘米).
答:这个扇形的面积约是18.84平方厘米,周长约是18.28厘米.
14.D [解析] ∵∠AOC∶∠AOD∶∠DOB=2∶7∶11,∠AOD+∠DOB=180°,
∴∠AOD=×180°=70°,∠DOB=110°,∠AOC=20°,
∴∠COD=∠AOC+∠AOD=90°.
∵OD=OC,CD=4,
∴在Rt△COD中,有2OD2=42,∴OD=2,
∴的长是==π.
15.D [解析] 如图,过点D作DH⊥AE于点H.
∵∠AOB=90°,OA=3,OB=2,
∴AB==.
由旋转的性质可知,OE=OB=2,DE=EF=AB=,△DHE≌△BOA,
∴DH=OB=2,
∴阴影部分的面积=△ADE的面积+△EOF的面积+扇形AOF的面积-扇形DEF的面积=×5×2+×2×3+-=8-π.
16.D [解析] 传送带上的物体A平移的距离为半径为30 cm的转动轮转过120°角的扇形的弧长,根据弧长公式可得:=20π(cm).
17.2π+2 [解析] ∵OA=AC=2,
∴AB=BC=CD=AD=,OC=4,
∴S阴影=π(42-22)+()2=2π+2.
18.解:(1)证明:如图,连结OC.
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠ACO=∠A=30°,∴∠OCD=90°.
又∵点C在半圆O上,
∴CD是半圆O的切线.
(2)∵∠A=30°,∴∠COB=2∠A=60°,
∴S扇形BOC==.
在Rt△OCD中,∵∠D=30°,OC=2,
∴OD=4,
∴CD==2,
∴SRt△OCD=OC·CD=×2×2=2,
∴图中阴影部分的面积为2-.
19.解:(1)证明:∵AB为☉O的直径,
∴∠ACB=90°.
∵OF⊥AC于点F,
∴∠AFO=90°,
∴∠ACB=∠AFO,
∴OF∥BC.
(2)证明:∵∠ACB=90°,
∴∠CAB+∠ABC=90°.
∵AB⊥CD于点E,∴∠CEB=90°,
∴∠ABC+∠BCE=90°,∴∠CAB=∠BCE.
又∵∠AFO=∠CEB=90°,OF=BE,
∴△AFO≌△CEB.
(3)连结OC.
∵AB为☉O的直径,CD是弦,AB⊥CD于点E,
∴∠OEC=90°,CE=CD=×10=5(cm).
在Rt△OCE中,OE=x cm,OC=OB=(5+x)cm,
由勾股定理,得OC2=CE2+OE2,
即(5+x)2=+x2,
解得x=5,∴OE=5 cm,OC=10 cm.
在Rt△OCE中,OC=2OE,故∠OCE=30°,
∴∠COE=60°.
由圆的轴对称性可知图中阴影部分的面积
S阴影=2(S扇形BOC-S△OCE)=2×
=cm2.
知识点 1 弧长公式及其应用
1.在半径为R的圆中,1°的圆心角所对的弧长l= ,n°的圆心角所对的弧长l= .
2.若扇形的圆心角为90°,半径为6,则该扇形的弧长为 ( )
A.π B.2π C.3π D.6π
3.如图1,AB是☉O的直径,D为☉O上一点,且∠ABD=30°,BO=4,则的长为 ( )
图1
A.π B.π C.2π D.π
4.已知扇形的圆心角为120°,弧长为2π,则它的半径为 .
5.[2020·金华] 如图2,的半径OA=2,OC⊥AB于点C,∠AOC=60°.
(1)求弦AB的长;
(2)求的长.
图2
知识点 2 扇形的面积公式及其应用
6.若一个扇形的圆心角为90°,半径为6,则该扇形的面积为 ( )
A. B.3π C.6π D.9π
7.如图3,在 ABCD中,∠B=60°,☉C的半径为3,则图中阴影部分的面积是 ( )
图3
A.π B.2π C.3π D.6π
8.钟面上分针的长为1,从上午9点到上午9点30分,分针在钟面上扫过的面积是 ( )
A.π B.π C.π D.π
9.如图4所示,分别以△ABC的三个顶点为圆心作☉A,☉B,☉C,且半径都是0.5 cm(三个圆两两不相交),则图中阴影部分的面积等于 ( )
图4
A. cm2 B. cm2 C. cm2 D. cm2
10.如图5,在矩形ABCD中,AB=4,AD=2,分别以点A,C为圆心,AD,CB长为半径画弧,交AB于点E,交CD于点F,则图中阴影部分的面积是 ( )
图5
A.4-2π B.8- C.8-2π D.8-4π
11.若一个扇形的面积为4π,它所对的圆心角为90°,则这个扇形的半径为 .
12.已知扇形的面积为2π,半径为3,则该扇形的弧长为 .(结果保留π)
13. 已知图6中扇形的半径为6厘米,求下列扇形的面积和周长.(π取3.14)
图6
【综合练习】
14.[2020·包头] 如图7,AB是☉O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC∶∠AOD∶∠DOB=2∶7∶11,CD=4,则的长为 ( )
图7
A.2π B.4π C.π D.π
15.如图8所示,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得到Rt△FOE,将线段EF绕点E逆时针旋转90°后得到线段ED,分别以点O,E为圆心,OA,EF长为半径画和,连结AD,则图中阴影部分的面积是 ( )
图8
A.π B. C.3+π D.8-π
16.如图9,当半径为30 cm的转动轮转过120°角时,传送带上的物体A平移的距离为 ( )
图9
A.900π cm B.300π cm C.60π cm D.20π cm
17.如图10所示,正方形ABCD的对角线AC所在的直线上有一点O,OA=AC=2,将正方形绕点O顺时针旋转60°,在旋转过程中,正方形扫过的图形(阴影部分)的面积是 .
图10
18.如图11所示,点D在半圆O的直径AB的延长线上,点C在半圆O上,AC=CD,
∠ACD=120°.
(1)求证:CD是半圆O的切线;
(2)若半圆O的半径为2,求图中阴影部分的面积.
图11
19.如图12,已知AB为☉O的直径,CD是弦,AB⊥CD于点E,OF⊥AC于点F,BE=OF.
(1)求证:OF∥BC;
(2)求证:△AFO≌△CEB;
(3)若EB=5 cm,CD=10 cm,设OE=x cm,求x的值及图中阴影部分的面积.
图12
27.3 第1课时 弧长和扇形的面积
1.
2.C [解析] 该扇形的弧长==3π.故选C.
3.D [解析] 如图,连结OD.
∵∠ABD=30°,
∴∠AOD=2∠ABD=60°,
∴∠BOD=120°,
∴的长==.
故选D.
4.3
5.解:(1)∵的半径OA=2,OC⊥AB于点C,∠AOC=60°,
∴AC=OA·sin60°=2×=,
∴AB=2AC=2.
(2)∵OA=OB,OC⊥AB,∠AOC=60°,
∴∠AOB=120°.
∵OA=2,
∴的长是=.
6.D
7.C [解析] ∵在 ABCD中,∠B=60°,
∴∠C=120°,
∴图中阴影部分的面积是=3π.
故选C.
8.A [解析] 钟面上分针的长为1,即R=1.从上午9点到上午9点30分,分针在钟面上绕着轴心旋转了180°,即n=180,所以S扇形===π.故选A.
9.B
10.C [解析] ∵矩形ABCD的面积为8,两个全等扇形面积之和为×π×22=2π,
∴阴影部分的面积为8-2π.
故选C.
11.4 [解析] ∵S=,
∴r2==16,
∴r=4.
12. [解析] 设扇形的弧长为l,则l×3=2π,解得l=.
13.[解析] (1)依据S=lr求面积.
(2)扇形的面积=×πr2,由此代入数据即可解决问题;扇形的周长=半径的长度×2+圆的周长×,据此代入数据即可求解.
解:(1)面积:×15.7×6=47.1(厘米2);
周长:6×2+15.7=12+15.7=27.7(厘米).
答:这个扇形的面积是47.1平方厘米,周长是27.7厘米.
(2)面积:×π×62≈×3.14×36=18.84(厘米2);
周长:6×2+π×6×2×≈12+6.28=18.28(厘米).
答:这个扇形的面积约是18.84平方厘米,周长约是18.28厘米.
14.D [解析] ∵∠AOC∶∠AOD∶∠DOB=2∶7∶11,∠AOD+∠DOB=180°,
∴∠AOD=×180°=70°,∠DOB=110°,∠AOC=20°,
∴∠COD=∠AOC+∠AOD=90°.
∵OD=OC,CD=4,
∴在Rt△COD中,有2OD2=42,∴OD=2,
∴的长是==π.
15.D [解析] 如图,过点D作DH⊥AE于点H.
∵∠AOB=90°,OA=3,OB=2,
∴AB==.
由旋转的性质可知,OE=OB=2,DE=EF=AB=,△DHE≌△BOA,
∴DH=OB=2,
∴阴影部分的面积=△ADE的面积+△EOF的面积+扇形AOF的面积-扇形DEF的面积=×5×2+×2×3+-=8-π.
16.D [解析] 传送带上的物体A平移的距离为半径为30 cm的转动轮转过120°角的扇形的弧长,根据弧长公式可得:=20π(cm).
17.2π+2 [解析] ∵OA=AC=2,
∴AB=BC=CD=AD=,OC=4,
∴S阴影=π(42-22)+()2=2π+2.
18.解:(1)证明:如图,连结OC.
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠ACO=∠A=30°,∴∠OCD=90°.
又∵点C在半圆O上,
∴CD是半圆O的切线.
(2)∵∠A=30°,∴∠COB=2∠A=60°,
∴S扇形BOC==.
在Rt△OCD中,∵∠D=30°,OC=2,
∴OD=4,
∴CD==2,
∴SRt△OCD=OC·CD=×2×2=2,
∴图中阴影部分的面积为2-.
19.解:(1)证明:∵AB为☉O的直径,
∴∠ACB=90°.
∵OF⊥AC于点F,
∴∠AFO=90°,
∴∠ACB=∠AFO,
∴OF∥BC.
(2)证明:∵∠ACB=90°,
∴∠CAB+∠ABC=90°.
∵AB⊥CD于点E,∴∠CEB=90°,
∴∠ABC+∠BCE=90°,∴∠CAB=∠BCE.
又∵∠AFO=∠CEB=90°,OF=BE,
∴△AFO≌△CEB.
(3)连结OC.
∵AB为☉O的直径,CD是弦,AB⊥CD于点E,
∴∠OEC=90°,CE=CD=×10=5(cm).
在Rt△OCE中,OE=x cm,OC=OB=(5+x)cm,
由勾股定理,得OC2=CE2+OE2,
即(5+x)2=+x2,
解得x=5,∴OE=5 cm,OC=10 cm.
在Rt△OCE中,OC=2OE,故∠OCE=30°,
∴∠COE=60°.
由圆的轴对称性可知图中阴影部分的面积
S阴影=2(S扇形BOC-S△OCE)=2×
=cm2.
