2021——2022学年华东师大版九年级数学下册27.4正多边形和圆练习题(word解析版)
文档属性
| 名称 | 2021——2022学年华东师大版九年级数学下册27.4正多边形和圆练习题(word解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 199.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 00:00:00 | ||
图片预览



文档简介
27.4 正多边形和圆
知识点 1 正多边形的定义
1.下列图形是正多边形的是 ( )
A.菱形 B.矩形 C.平行四边形 D.正方形
2.下列说法中正确的是 ( )
A.各边相等的多边形是正多边形
B.各角相等的多边形是正多边形
C.各边相等的圆内接多边形是正多边形
D.各角相等的圆内接多边形是正多边形
知识点 2 正多边形的有关计算
3.边长为10的正六边形的半径是 ( )
A.5 B.10 C.15 D.20
4.如图1,☉O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是 ( )
图1
A.72° B.60° C.54° D.36°
5.如图2,已知正五边形ABCDE内接于☉O,连结BD,则∠ABD的度数是 ( )
图2
A.60° B.70° C.72° D.144°
6.边长为2的圆内接正三角形的边心距是 ( )
A.1 B. C. D.
7.已知正六边形的边长为2,则它的内切圆的半径为 ( )
A.1 B. C.2 D.2
8.如图3,四边形ABCD是☉O的内接正方形,若正方形的面积等于4,则☉O的面积等于 .
图3
9.若一个正n边形的中心角是它的一个内角的,则n= .
10.如图4,☉O是正五边形ABCDE的外接圆,F是的中点,连结CF,EF.
(1)请直接写出∠CFE= °;
(2)求证:EF=CF;
(3)若☉O的半径为5,求的长.
图4
知识点 3 画正多边形
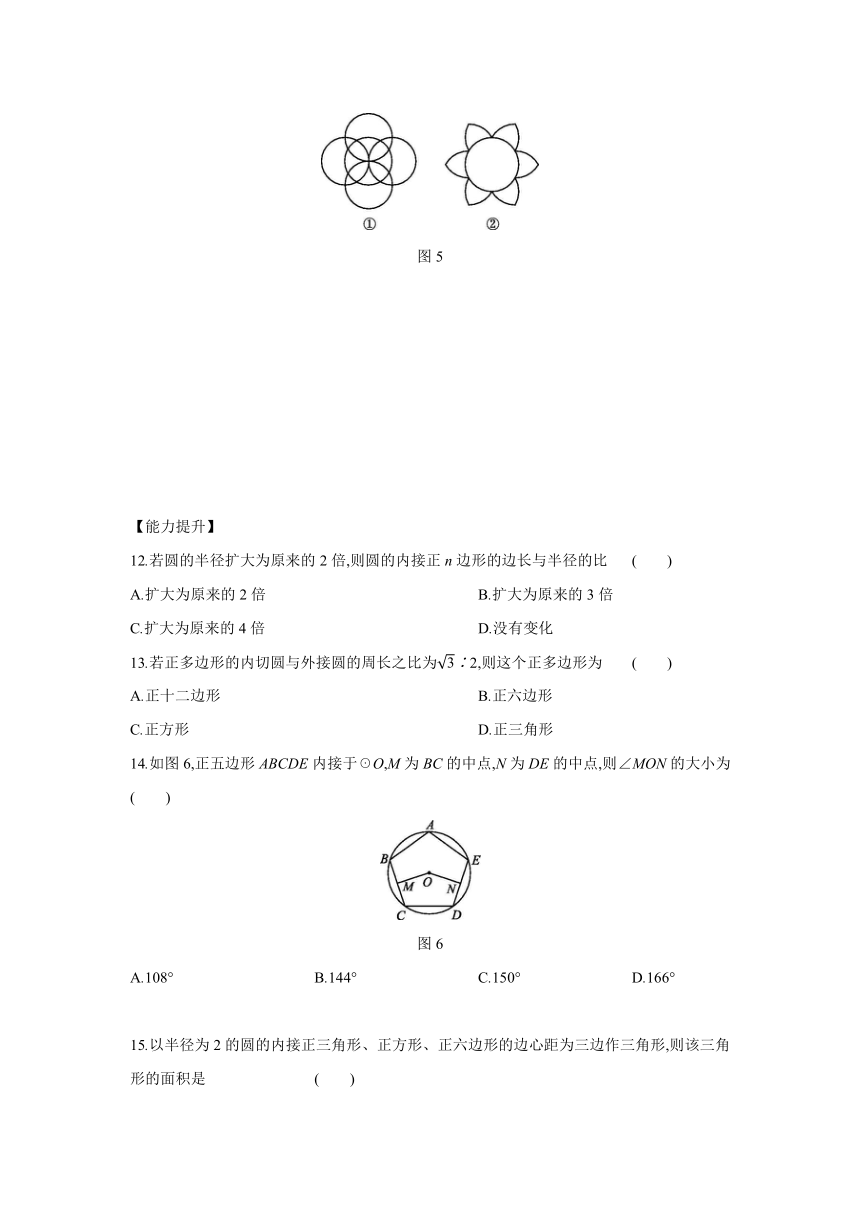
11.用等分圆周的方法画出下列图案.
图5
【能力提升】
12.若圆的半径扩大为原来的2倍,则圆的内接正n边形的边长与半径的比 ( )
A.扩大为原来的2倍 B.扩大为原来的3倍
C.扩大为原来的4倍 D.没有变化
13.若正多边形的内切圆与外接圆的周长之比为∶2,则这个正多边形为 ( )
A.正十二边形 B.正六边形
C.正方形 D.正三角形
14.如图6,正五边形ABCDE内接于☉O,M为BC的中点,N为DE的中点,则∠MON的大小为 ( )
图6
A.108° B.144° C.150° D.166°
15.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是 ( )
A. B. C. D.
16.[2020·徐州] 如图7,A,B,C,D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为 .
图7
17.如图8,四边形ABCD是☉O的内接正方形,E为边CD上的一点,且DE=CE,连结BE并延长交☉O于点F,连结FC.若正方形的边长为1,求弦FC的长.
图8
18.如图9所示,将边长为2的正六边形A1A2A3A4A5A6在直线l上由①的位置按顺时针方向向右作无滑动的滚动.
(1)该正六边形的每一个内角的度数是 , 每一个外角的度数是 ;
(2)求它的对角线A1A5,A2A4,A1A3的长;
(3)写出正六边形A1A2A3A4A5A6从①的位置第一次滚动到②的位置时,顶点A1所经过的路径长.
图9
27.4 正多边形和圆
1.D [解析] 根据各边相等、各角也相等的多边形是正多边形得选项D符合.
2.C [解析] ∵各边相等、各角也相等的多边形叫做正多边形,∴A,B错误.∵各边相等的圆内接多边形的各角一定相等,∴C正确.∵各角相等的圆内接多边形的边不一定相等,∴D错误.
故选C.
3.B [解析] 因为正六边形的中心角是60°,所以正六边形的边与两条半径构成的三角形是等边三角形,所以正六边形的半径是10.
4.A [解析] ∵☉O是正五边形ABCDE的外接圆,∴∠AOB=360°÷5=72°.
5.C
6.D [解析] 设边心距为r,则r=1×tan30°=.
7.B [解析] 如图,连结OA,OB,OG.
∵六边形ABCDEF是边长为2的正六边形,
∴△OAB是等边三角形,
∴OA=AB=2,
∴OG=OA·sin60°=2×=,
∴边长为2的正六边形的内切圆的半径为.
8.2π [解析] 由题意易知正方形的边长AB=2,则☉O的半径是2×=,则☉O的面积是()2π=2π.
9.12
10.解:(1)∵五边形ABCDE是正五边形,
∴∠EDC=108°,
∴∠CFE=180°-108°=72°.
故答案为72.
(2)证明:∵五边形ABCDE是正五边形,
∴AE=BC,∴=.
∵F是的中点,∴=,
∴+=+,
即=,∴EF=CF.
(3)∵☉O是正五边形ABCDE的外接圆,
∴====,
∴==×2πr=2π.
又∵==π,
∴=+=3π.
11.解:图略.画法:(1)先画一个圆,然后分别以圆的4等分点为圆心,以圆的半径为半径再画4个圆,即可得到题图①的图案.
(2)先画一个圆,然后分别以圆的6等分点为圆心,以圆的半径为半径画弧,即可得到题图②的图案.
12.D
13.B [解析] 如图.
因为正多边形的内切圆与外接圆的周长之比为∶2,所以这两个圆的半径之比为∶2.
设AB是正多边形的一边,O为两个圆的圆心,OC⊥AB,
不妨设OC=,OA=OB=2,
则在Rt△AOC中,cos∠AOC==,
∴∠AOC=30°,∴∠AOB=60°,
则正多边形的边数是=6,
故这个正多边形为正六边形.
14.B [解析] ∵M为BC的中点,N为DE的中点,
∴OM⊥BC,ON⊥DE,
∴∠OMC=∠OND=90°.
∵五边形ABCDE是正五边形,
∴∠C=∠D=(5-2)×180°÷5=108°,
∴∠MON=(5-2)×180°-2×90°-2×108°=144°.
故选B.
15.A [解析] 如图①,∵OC=2,
∴OD=2×sin30°=1.
如图②,∵OB=2,
∴OE=2×sin45°=.
如图③,∵OA=2,
∴OD=2×cos30°=.
则该三角形的三边长分别为1,,.
∵12+()2=()2,
∴该三角形是直角三角形,
∴该三角形的面积是×1×=.故选A.
16.10 [解析] 如图,连结OA,OB.
∵A,B,C,D为一个正多边形的顶点,O为正多边形的中心,
∴点A,B,C,D在以点O为圆心,OA为半径的同一个圆上.
∵∠ADB=18°,
∴∠AOB=2∠ADB=36°,
∴这个正多边形的边数==10.
17.解:如图,连结BD.
∵CE=DE=CD=×1=,
∴BE==.
在Rt△ABD中,DB==.
∵∠FCE=∠DBE,∠CFE=∠BDE,
∴△FEC∽△DEB,∴=,
即=,∴FC=.
18.解:(1)120° 60°
(2)连结A1A3,过点A2作A2M⊥A1A3于点M,如图 所示.
根据正六边形的性质,得A1A5=A2A4=A1A3,A1A2=A3A2,∠A1A2A3=120°,∴A1M=A3M,∠1=30°,
∴A2M=A1A2=1.
由勾股定理,得A1M==,
∴A1A5=A2A4=A1A3=2.
(3)连结A1A5,A1A4,A1A3,如图 所示.
由(2)得:A1A5=A1A3=2.易知A1A4=4.
当正六边形A1A2A3A4A5A6从①的位置第一次滚动到②的位置时,顶点A1所经过的路径长是以A6,A5,A4,A3,A2为圆心,以2,2,4,2,2为半径,圆心角都为60°的五条弧的长度之和,
∴顶点A1所经过的路径长=++++==π.
知识点 1 正多边形的定义
1.下列图形是正多边形的是 ( )
A.菱形 B.矩形 C.平行四边形 D.正方形
2.下列说法中正确的是 ( )
A.各边相等的多边形是正多边形
B.各角相等的多边形是正多边形
C.各边相等的圆内接多边形是正多边形
D.各角相等的圆内接多边形是正多边形
知识点 2 正多边形的有关计算
3.边长为10的正六边形的半径是 ( )
A.5 B.10 C.15 D.20
4.如图1,☉O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是 ( )
图1
A.72° B.60° C.54° D.36°
5.如图2,已知正五边形ABCDE内接于☉O,连结BD,则∠ABD的度数是 ( )
图2
A.60° B.70° C.72° D.144°
6.边长为2的圆内接正三角形的边心距是 ( )
A.1 B. C. D.
7.已知正六边形的边长为2,则它的内切圆的半径为 ( )
A.1 B. C.2 D.2
8.如图3,四边形ABCD是☉O的内接正方形,若正方形的面积等于4,则☉O的面积等于 .
图3
9.若一个正n边形的中心角是它的一个内角的,则n= .
10.如图4,☉O是正五边形ABCDE的外接圆,F是的中点,连结CF,EF.
(1)请直接写出∠CFE= °;
(2)求证:EF=CF;
(3)若☉O的半径为5,求的长.
图4
知识点 3 画正多边形
11.用等分圆周的方法画出下列图案.
图5
【能力提升】
12.若圆的半径扩大为原来的2倍,则圆的内接正n边形的边长与半径的比 ( )
A.扩大为原来的2倍 B.扩大为原来的3倍
C.扩大为原来的4倍 D.没有变化
13.若正多边形的内切圆与外接圆的周长之比为∶2,则这个正多边形为 ( )
A.正十二边形 B.正六边形
C.正方形 D.正三角形
14.如图6,正五边形ABCDE内接于☉O,M为BC的中点,N为DE的中点,则∠MON的大小为 ( )
图6
A.108° B.144° C.150° D.166°
15.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是 ( )
A. B. C. D.
16.[2020·徐州] 如图7,A,B,C,D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为 .
图7
17.如图8,四边形ABCD是☉O的内接正方形,E为边CD上的一点,且DE=CE,连结BE并延长交☉O于点F,连结FC.若正方形的边长为1,求弦FC的长.
图8
18.如图9所示,将边长为2的正六边形A1A2A3A4A5A6在直线l上由①的位置按顺时针方向向右作无滑动的滚动.
(1)该正六边形的每一个内角的度数是 , 每一个外角的度数是 ;
(2)求它的对角线A1A5,A2A4,A1A3的长;
(3)写出正六边形A1A2A3A4A5A6从①的位置第一次滚动到②的位置时,顶点A1所经过的路径长.
图9
27.4 正多边形和圆
1.D [解析] 根据各边相等、各角也相等的多边形是正多边形得选项D符合.
2.C [解析] ∵各边相等、各角也相等的多边形叫做正多边形,∴A,B错误.∵各边相等的圆内接多边形的各角一定相等,∴C正确.∵各角相等的圆内接多边形的边不一定相等,∴D错误.
故选C.
3.B [解析] 因为正六边形的中心角是60°,所以正六边形的边与两条半径构成的三角形是等边三角形,所以正六边形的半径是10.
4.A [解析] ∵☉O是正五边形ABCDE的外接圆,∴∠AOB=360°÷5=72°.
5.C
6.D [解析] 设边心距为r,则r=1×tan30°=.
7.B [解析] 如图,连结OA,OB,OG.
∵六边形ABCDEF是边长为2的正六边形,
∴△OAB是等边三角形,
∴OA=AB=2,
∴OG=OA·sin60°=2×=,
∴边长为2的正六边形的内切圆的半径为.
8.2π [解析] 由题意易知正方形的边长AB=2,则☉O的半径是2×=,则☉O的面积是()2π=2π.
9.12
10.解:(1)∵五边形ABCDE是正五边形,
∴∠EDC=108°,
∴∠CFE=180°-108°=72°.
故答案为72.
(2)证明:∵五边形ABCDE是正五边形,
∴AE=BC,∴=.
∵F是的中点,∴=,
∴+=+,
即=,∴EF=CF.
(3)∵☉O是正五边形ABCDE的外接圆,
∴====,
∴==×2πr=2π.
又∵==π,
∴=+=3π.
11.解:图略.画法:(1)先画一个圆,然后分别以圆的4等分点为圆心,以圆的半径为半径再画4个圆,即可得到题图①的图案.
(2)先画一个圆,然后分别以圆的6等分点为圆心,以圆的半径为半径画弧,即可得到题图②的图案.
12.D
13.B [解析] 如图.
因为正多边形的内切圆与外接圆的周长之比为∶2,所以这两个圆的半径之比为∶2.
设AB是正多边形的一边,O为两个圆的圆心,OC⊥AB,
不妨设OC=,OA=OB=2,
则在Rt△AOC中,cos∠AOC==,
∴∠AOC=30°,∴∠AOB=60°,
则正多边形的边数是=6,
故这个正多边形为正六边形.
14.B [解析] ∵M为BC的中点,N为DE的中点,
∴OM⊥BC,ON⊥DE,
∴∠OMC=∠OND=90°.
∵五边形ABCDE是正五边形,
∴∠C=∠D=(5-2)×180°÷5=108°,
∴∠MON=(5-2)×180°-2×90°-2×108°=144°.
故选B.
15.A [解析] 如图①,∵OC=2,
∴OD=2×sin30°=1.
如图②,∵OB=2,
∴OE=2×sin45°=.
如图③,∵OA=2,
∴OD=2×cos30°=.
则该三角形的三边长分别为1,,.
∵12+()2=()2,
∴该三角形是直角三角形,
∴该三角形的面积是×1×=.故选A.
16.10 [解析] 如图,连结OA,OB.
∵A,B,C,D为一个正多边形的顶点,O为正多边形的中心,
∴点A,B,C,D在以点O为圆心,OA为半径的同一个圆上.
∵∠ADB=18°,
∴∠AOB=2∠ADB=36°,
∴这个正多边形的边数==10.
17.解:如图,连结BD.
∵CE=DE=CD=×1=,
∴BE==.
在Rt△ABD中,DB==.
∵∠FCE=∠DBE,∠CFE=∠BDE,
∴△FEC∽△DEB,∴=,
即=,∴FC=.
18.解:(1)120° 60°
(2)连结A1A3,过点A2作A2M⊥A1A3于点M,如图 所示.
根据正六边形的性质,得A1A5=A2A4=A1A3,A1A2=A3A2,∠A1A2A3=120°,∴A1M=A3M,∠1=30°,
∴A2M=A1A2=1.
由勾股定理,得A1M==,
∴A1A5=A2A4=A1A3=2.
(3)连结A1A5,A1A4,A1A3,如图 所示.
由(2)得:A1A5=A1A3=2.易知A1A4=4.
当正六边形A1A2A3A4A5A6从①的位置第一次滚动到②的位置时,顶点A1所经过的路径长是以A6,A5,A4,A3,A2为圆心,以2,2,4,2,2为半径,圆心角都为60°的五条弧的长度之和,
∴顶点A1所经过的路径长=++++==π.
