2021—2022学年北师大版九年级数学下册3.3垂径定理同步练习(word解析版)
文档属性
| 名称 | 2021—2022学年北师大版九年级数学下册3.3垂径定理同步练习(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 198.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 12:16:01 | ||
图片预览



文档简介
3.3 垂径定理
【基础练习】
知识点1 垂径定理
1.如图1,CD是☉O的直径,弦AB⊥CD于点F,则下列结论不一定正确的是 ( )
图1
A.= B.AF=BF
C.OF=CF D.=
2.如图2,☉O的半径为5,AB为弦,半径OC⊥AB,垂足为E,若OE=3,则AB的长是( )
图2
A.4 B.6 C.8 D.10
3.[2021·柳州]往水平放置的半径为13cm的圆柱形容器内装入一些水以后,截面图如图3所示,若水面宽度AB=24cm,则水的最大深度为 ( )
图3
A.5cm B.8cm C.10cm D.12cm
4.如图4,AB是☉O的直径,弦CD⊥AB于点E,OC=5cm,CD=6cm,则AE= cm.
图4
5.如图5,AB是☉O的弦,OC⊥AB,垂足为C,将劣弧沿弦AB折叠交OC于其中点D,若AB=2,则☉O的半径为 .
图5
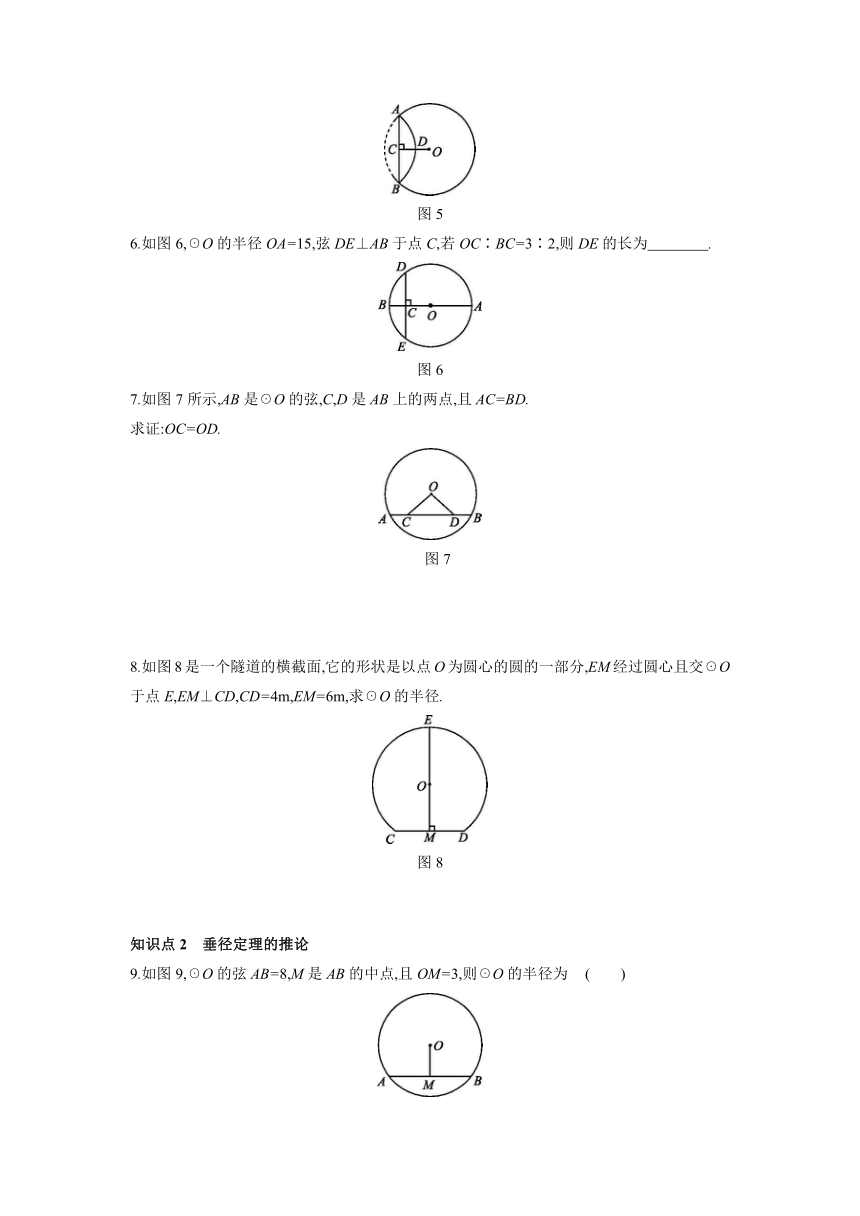
6.如图6,☉O的半径OA=15,弦DE⊥AB于点C,若OC∶BC=3∶2,则DE的长为 .
图6
7.如图7所示,AB是☉O的弦,C,D是AB上的两点,且AC=BD.
求证:OC=OD.
图7
8.如图8是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,EM经过圆心且交☉O于点E,EM⊥CD,CD=4m,EM=6m,求☉O的半径.
图8
知识点2 垂径定理的推论
9.如图9,☉O的弦AB=8,M是AB的中点,且OM=3,则☉O的半径为 ( )
图9
A.8 B.2 C.10 D.5
10.如图10,AB是☉O的直径,弦CD交AB于点M,且CM=DM,则下列结论不一定成立的是( )
图10
A.AB⊥CD B.CB=DB C.∠ACD=∠ADC D.OM=MD
11.下列说法中正确的是 ( )
A.平分弦的直径平分弦所对的两条弧
B.弦的垂直平分线平分它所对的两条弧,但不一定过圆心
C.过弦的中点的直径垂直于弦
D.平分弦所对的两条弧的直径平分弦
【能力提升】
12.如图11,AB是☉O的直径,且经过弦CD的中点H,已知sin∠CDB=,BD=5,则AH的长为 ( )
图11
A. B. C. D.
13.如图12,AC是☉O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F,若BD=8cm,AE=2cm,则OF的长度是 ( )
图12
A.3cm B.cm C.2.5cm D.cm
14.已知☉O的半径为10cm,AB,CD是☉O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是 cm.
15.如图13,在☉O中,弦AB的垂直平分线交☉O于C,D两点,AB=8,弦AC=5,求☉O的直径.
图13
16.[教材随堂练习第1题变式题]如图14,有一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施.若某次洪水中,拱顶离水面只有4m,即PN=4m,试通过计算说明此时是否需要采取紧急措施.
图14
17.如图15,在半径为的☉O中,弦AB与CD交于点E,已知AB=6,AE=1.若∠DEB=75°,求CD的长.
图15
答案
1.C [解析]∵CD是☉O的直径,弦AB⊥CD,垂足为F,∴=,=,F为AB的中点,即AF=BF,故选项A,B,D正确;而OF与CF不一定相等.故选C.
2.C [解析]连接OA,如图.
∵OC⊥AB,OA=5,OE=3,
∴AE===4,
∴AB=2AE=8.故选C.
3.B [解析]连接OB,过点O作OC⊥AB于点D,交☉O于点C.
∵AB=24cm,∴BD=AB=12(cm).
在Rt△OBD中,OD===5(cm),
∴CD=OC-OD=13-5=8(cm),
即水的最大深度为8cm.
故选B.
4.9
5.3
6.24 [解析]如图,连接OD.
∵OA=OB=15,OC∶BC=3∶2,
∴OC=9.
∵DE⊥AB,∴∠DCO=90°,DE=2CD.
在Rt△OCD中,CD===12,
∴DE=2CD=24.
故答案为24.
7.证明:过点O作OE⊥AB于点E,则AE=BE.
又∵AC=BD,∴CE=DE,
∴OE垂直平分CD,∴OC=OD.
8.解:如图,连接OC.
∵EM⊥CD,EM经过圆心,CD=4m,
∴CM=CD=2m.
设☉O的半径是xm.
在Rt△COM中,有OC2=CM2+OM2,
即x2=22+(6-x)2,解得x=,
即☉O的半径是m.
9.D
10.D [解析]∵AB是☉O的直径,CM=DM,∴CD⊥AB,=,∴CB=DB,AB垂直平分CD,∴AC=AD,∴∠ACD=∠ADC,而推不出OM与MD相等.故选D.
11.D 12.B
13.D [解析]如图,连接AB,OB.
∵AC是☉O的直径,弦BD⊥AO于点E,BD=8cm,AE=2cm,
∴BE=BD=4cm.
在Rt△ABE中,AE2+BE2=AB2,
即AB==2(cm).
∵OB=OC,OF⊥BC,
∴BF=FC.
又∵OA=OC,
∴OF=AB=cm.故选D.
14.2或14
15.解:由题意得CD是☉O的直径,如图,设AB,CD相交于点E,连接AO.
∵AB⊥CD,∴AE=AB=4.
在Rt△ACE中,CE==3.
由勾股定理得AO2=AE2+OE2.
设AO=R,则R2=42+(R-3)2,
解得R=,
∴☉O的直径为.
16.解:设圆弧形拱桥所在圆的半径为xm,
则OA=OA'=OP=xm,
OM=OP-PM=(x-18)m.
易得AM=BM,A'N=B'N,OP⊥AB,OP⊥A'B'.
∵AB=60m,∴AM=30m.
在Rt△AOM中,由勾股定理,得OA2=OM2+AM2,
即x2=(x-18)2+302,解得x=34,
∴ON=OP-PN=34-4=30(m).
在Rt△A'ON中,由勾股定理,得A'N===16(m),
∴A'B'=32m>30m,
∴此时不需要采取紧急措施.
17.解:过点O作OF⊥CD于点F,OG⊥AB于点G,连接OB,OD,OE,如图所示.
则DF=CF,AG=BG=AB=3,
∴EG=AG-AE=2.
在Rt△BOG中,OG===2,
∴EG=OG,OE==2,
∴△EOG是等腰直角三角形,
∴∠OEG=45°.
又∵∠DEB=75°,
∴∠OEF=30°,
∴OF=OE=.
在Rt△ODF中,DF===,
∴CD=2DF=2.
【基础练习】
知识点1 垂径定理
1.如图1,CD是☉O的直径,弦AB⊥CD于点F,则下列结论不一定正确的是 ( )
图1
A.= B.AF=BF
C.OF=CF D.=
2.如图2,☉O的半径为5,AB为弦,半径OC⊥AB,垂足为E,若OE=3,则AB的长是( )
图2
A.4 B.6 C.8 D.10
3.[2021·柳州]往水平放置的半径为13cm的圆柱形容器内装入一些水以后,截面图如图3所示,若水面宽度AB=24cm,则水的最大深度为 ( )
图3
A.5cm B.8cm C.10cm D.12cm
4.如图4,AB是☉O的直径,弦CD⊥AB于点E,OC=5cm,CD=6cm,则AE= cm.
图4
5.如图5,AB是☉O的弦,OC⊥AB,垂足为C,将劣弧沿弦AB折叠交OC于其中点D,若AB=2,则☉O的半径为 .
图5
6.如图6,☉O的半径OA=15,弦DE⊥AB于点C,若OC∶BC=3∶2,则DE的长为 .
图6
7.如图7所示,AB是☉O的弦,C,D是AB上的两点,且AC=BD.
求证:OC=OD.
图7
8.如图8是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,EM经过圆心且交☉O于点E,EM⊥CD,CD=4m,EM=6m,求☉O的半径.
图8
知识点2 垂径定理的推论
9.如图9,☉O的弦AB=8,M是AB的中点,且OM=3,则☉O的半径为 ( )
图9
A.8 B.2 C.10 D.5
10.如图10,AB是☉O的直径,弦CD交AB于点M,且CM=DM,则下列结论不一定成立的是( )
图10
A.AB⊥CD B.CB=DB C.∠ACD=∠ADC D.OM=MD
11.下列说法中正确的是 ( )
A.平分弦的直径平分弦所对的两条弧
B.弦的垂直平分线平分它所对的两条弧,但不一定过圆心
C.过弦的中点的直径垂直于弦
D.平分弦所对的两条弧的直径平分弦
【能力提升】
12.如图11,AB是☉O的直径,且经过弦CD的中点H,已知sin∠CDB=,BD=5,则AH的长为 ( )
图11
A. B. C. D.
13.如图12,AC是☉O的直径,弦BD⊥AO于点E,连接BC,过点O作OF⊥BC于点F,若BD=8cm,AE=2cm,则OF的长度是 ( )
图12
A.3cm B.cm C.2.5cm D.cm
14.已知☉O的半径为10cm,AB,CD是☉O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是 cm.
15.如图13,在☉O中,弦AB的垂直平分线交☉O于C,D两点,AB=8,弦AC=5,求☉O的直径.
图13
16.[教材随堂练习第1题变式题]如图14,有一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施.若某次洪水中,拱顶离水面只有4m,即PN=4m,试通过计算说明此时是否需要采取紧急措施.
图14
17.如图15,在半径为的☉O中,弦AB与CD交于点E,已知AB=6,AE=1.若∠DEB=75°,求CD的长.
图15
答案
1.C [解析]∵CD是☉O的直径,弦AB⊥CD,垂足为F,∴=,=,F为AB的中点,即AF=BF,故选项A,B,D正确;而OF与CF不一定相等.故选C.
2.C [解析]连接OA,如图.
∵OC⊥AB,OA=5,OE=3,
∴AE===4,
∴AB=2AE=8.故选C.
3.B [解析]连接OB,过点O作OC⊥AB于点D,交☉O于点C.
∵AB=24cm,∴BD=AB=12(cm).
在Rt△OBD中,OD===5(cm),
∴CD=OC-OD=13-5=8(cm),
即水的最大深度为8cm.
故选B.
4.9
5.3
6.24 [解析]如图,连接OD.
∵OA=OB=15,OC∶BC=3∶2,
∴OC=9.
∵DE⊥AB,∴∠DCO=90°,DE=2CD.
在Rt△OCD中,CD===12,
∴DE=2CD=24.
故答案为24.
7.证明:过点O作OE⊥AB于点E,则AE=BE.
又∵AC=BD,∴CE=DE,
∴OE垂直平分CD,∴OC=OD.
8.解:如图,连接OC.
∵EM⊥CD,EM经过圆心,CD=4m,
∴CM=CD=2m.
设☉O的半径是xm.
在Rt△COM中,有OC2=CM2+OM2,
即x2=22+(6-x)2,解得x=,
即☉O的半径是m.
9.D
10.D [解析]∵AB是☉O的直径,CM=DM,∴CD⊥AB,=,∴CB=DB,AB垂直平分CD,∴AC=AD,∴∠ACD=∠ADC,而推不出OM与MD相等.故选D.
11.D 12.B
13.D [解析]如图,连接AB,OB.
∵AC是☉O的直径,弦BD⊥AO于点E,BD=8cm,AE=2cm,
∴BE=BD=4cm.
在Rt△ABE中,AE2+BE2=AB2,
即AB==2(cm).
∵OB=OC,OF⊥BC,
∴BF=FC.
又∵OA=OC,
∴OF=AB=cm.故选D.
14.2或14
15.解:由题意得CD是☉O的直径,如图,设AB,CD相交于点E,连接AO.
∵AB⊥CD,∴AE=AB=4.
在Rt△ACE中,CE==3.
由勾股定理得AO2=AE2+OE2.
设AO=R,则R2=42+(R-3)2,
解得R=,
∴☉O的直径为.
16.解:设圆弧形拱桥所在圆的半径为xm,
则OA=OA'=OP=xm,
OM=OP-PM=(x-18)m.
易得AM=BM,A'N=B'N,OP⊥AB,OP⊥A'B'.
∵AB=60m,∴AM=30m.
在Rt△AOM中,由勾股定理,得OA2=OM2+AM2,
即x2=(x-18)2+302,解得x=34,
∴ON=OP-PN=34-4=30(m).
在Rt△A'ON中,由勾股定理,得A'N===16(m),
∴A'B'=32m>30m,
∴此时不需要采取紧急措施.
17.解:过点O作OF⊥CD于点F,OG⊥AB于点G,连接OB,OD,OE,如图所示.
则DF=CF,AG=BG=AB=3,
∴EG=AG-AE=2.
在Rt△BOG中,OG===2,
∴EG=OG,OE==2,
∴△EOG是等腰直角三角形,
∴∠OEG=45°.
又∵∠DEB=75°,
∴∠OEF=30°,
∴OF=OE=.
在Rt△ODF中,DF===,
∴CD=2DF=2.
