2021-2022学年北师大版九年级数学下册3.9 弧长及扇形的面积同步练习(Word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.9 弧长及扇形的面积同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 181.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 13:35:56 | ||
图片预览


文档简介
9 弧长及扇形的面积
【基础练习】
知识点1 弧长公式及其应用
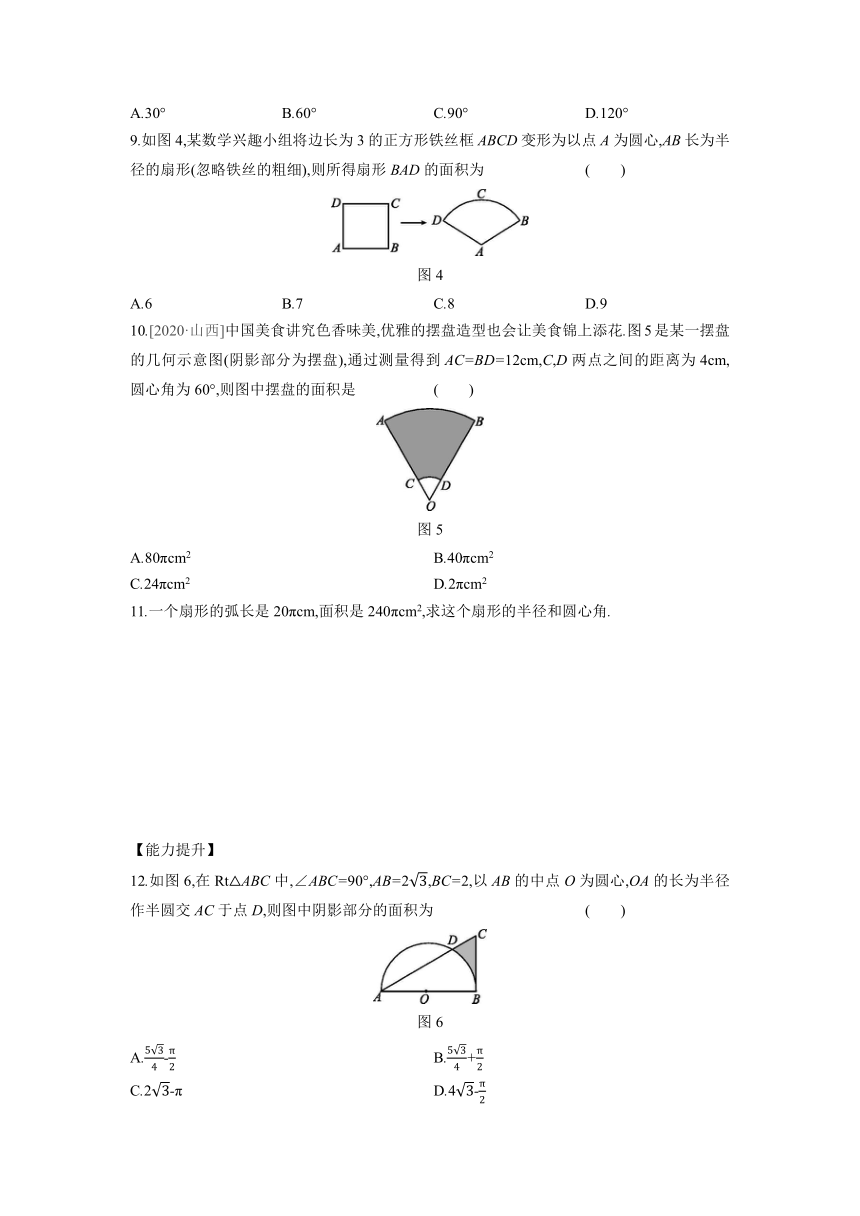
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为 ( )
A.π B.2π C.3π D.6π
2.一个扇形的圆心角为60°,它的弧长为2πcm,则这个扇形的半径为 ( )
A.6cm B.12cm
C.2cm D.cm
3.一个扇形的半径为8cm,弧长为πcm,则这个扇形的圆心角为 ( )
A.60° B.120° C.150° D.180°
4.如图1,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=6,则的长为 ( )
图1
A. B. C.2π D.2π
5.如图2,将☉O沿弦AB折叠,使恰好经过圆心O,若的长为2π,则☉O的半径为 .
图2
6.制造弯形管道时,经常要先按中心线计算“展直长度”,再下料.图3是一段管道,其中∠O=∠O'=90°,中心线的两条弧的半径都是1000mm,求这段管道的展直长度.(π≈3.14)
图3
知识点2 扇形的面积公式及其应用
7.已知扇形的圆心角为120°,半径为3,则该扇形的面积为 ( )
A.2π B.3π C.6π D.12π
8.若一个扇形的半径是18cm,面积是54πcm2,则该扇形的圆心角为 ( )
A.30° B.60° C.90° D.120°
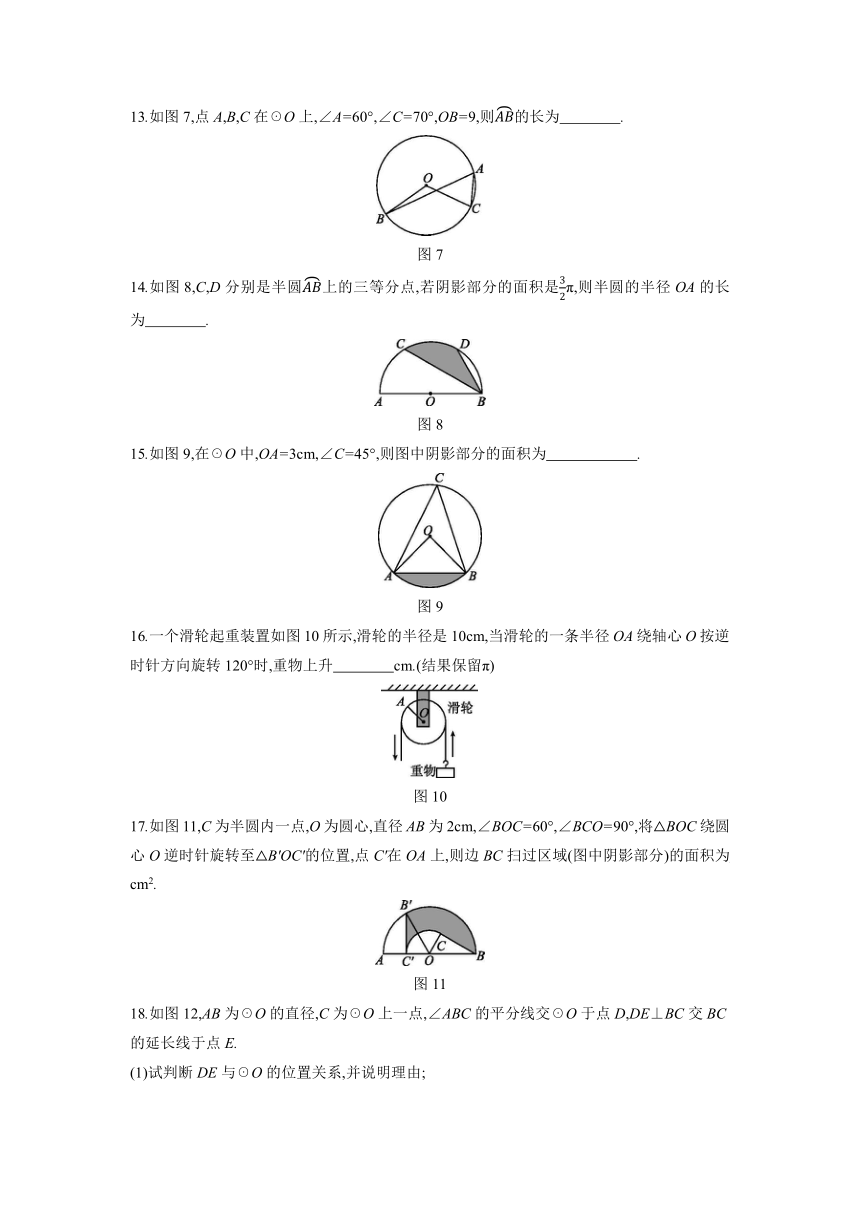
9.如图4,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以点A为圆心,AB长为半径的扇形(忽略铁丝的粗细),则所得扇形BAD的面积为 ( )
图4
A.6 B.7 C.8 D.9
10.[2020·山西]中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图5是某一摆盘的几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C,D两点之间的距离为4cm,圆心角为60°,则图中摆盘的面积是 ( )
图5
A.80πcm2 B.40πcm2
C.24πcm2 D.2πcm2
11.一个扇形的弧长是20πcm,面积是240πcm2,求这个扇形的半径和圆心角.
【能力提升】
12.如图6,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点O为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为 ( )
图6
A.- B.+
C.2-π D.4-
13.如图7,点A,B,C在☉O上,∠A=60°,∠C=70°,OB=9,则的长为 .
图7
14.如图8,C,D分别是半圆上的三等分点,若阴影部分的面积是π,则半圆的半径OA的长为 .
图8
15.如图9,在☉O中,OA=3cm,∠C=45°,则图中阴影部分的面积为 .
图9
16.一个滑轮起重装置如图10所示,滑轮的半径是10cm,当滑轮的一条半径OA绕轴心O按逆时针方向旋转120°时,重物上升 cm.(结果保留π)
图10
17.如图11,C为半圆内一点,O为圆心,直径AB为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B'OC'的位置,点C'在OA上,则边BC扫过区域(图中阴影部分)的面积为 cm2.
图11
18.如图12,AB为☉O的直径,C为☉O上一点,∠ABC的平分线交☉O于点D,DE⊥BC交BC的延长线于点E.
(1)试判断DE与☉O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3,DF=3,求图中阴影部分的面积.
图12
19.问题:已知α,β均为锐角,tanα=,tanβ=,求α+β的度数.
探究:用6个小正方形构造如图13所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;
延伸:设经过图中M,P,H三点的圆弧与AH交于点R,求的长度.
图13
答案
1.C
2.A [解析]根据弧长公式,得πr=2π,解得r=6.
3.B 4.B
5.3 [解析]连接OA,OB,过点O作OC⊥AB于点C,如图.
由题意得OC=OA.
则在Rt△OAC中,sin∠OAC==,
∴∠OAC=30°.
∵OA=OB,
∴∠OBA=∠OAC=30°,
∴∠AOB=120°.
设☉O的半径为r.
则的长为=2π,
∴r=3.
6.解:这段管道的展直长度为2×+3000=1000π+3000≈1000×3.14+3000=6140(mm).
7.B [解析]S扇形==3π.
8.B [解析]设扇形的圆心角为n°,则=54π,解得n=60.故选B.
9.D [解析]∵正方形的边长为3,
∴弧BD的长为6,
∴S扇形BAD=lr=×6×3=9.故选D.
10.B [解析]如图,连接CD.
∵OC=OD,∠O=60°,
∴△COD是等边三角形,
∴OC=OD=CD=4cm,
∴S阴影=S扇形OAB-S扇形OCD=-=40π(cm2).
故选B.
11.解:设这个扇形的半径为Rcm,圆心角为n°.
∵S扇形=lR,∴240π=×20π×R,
解得R=24.
∵l=,
∴20π=,解得n=150.
因此这个扇形的半径为24cm,圆心角为150°.
12.A
13.8π
14.3 [解析]如图,连接OC,OD,CD.
∵△COD和△BCD同底等高,
∴S△COD=S△BCD.
∴阴影部分的面积=S扇形OCD.
∵C,D为半圆的三等分点,
∴∠COD=180°÷3=60°.
又∵阴影部分的面积是π,
∴=π,
∴r=3.
15.π-cm2 [解析]∵∠C=45°,
∴∠AOB=90°.
∵OA=OB=3,
∴S阴影=S扇形OAB-S△OAB=-×3×3=-cm2.
16.π [解析]l==π(cm).
故答案为π.
17.π
18.解:(1)DE与☉O相切.理由:连接DO,如图.
∵DO=BO,
∴∠ODB=∠OBD.
∵∠ABC的平分线交☉O于点D,
∴∠EBD=∠OBD,
∴∠EBD=∠ODB,∴DO∥BE.
∵DE⊥BC,∴DO⊥DE.
又∵OD是☉O的半径,∴DE与☉O相切.
(2)∵∠ABC的平分线交☉O于点D,DE⊥BE,DF⊥AB,∴DE=DF=3.
∵BE=3,∴BD==6,
∴sin∠DBF==,∴∠DBF=30°,
∴∠DOF=60°,
∴sin60°===,cos60°==,
∴DO=2,FO=,
故图中阴影部分的面积为-×3=2π-.
19.解:探究:如图,连接AM,MH,则∠MHP=∠α.
∵AD=MC,∠D=∠C,MD=HC,
∴△ADM≌△MCH,
∴AM=MH,∠DAM=∠HMC.
∵∠AMD+∠DAM=90°,
∴∠AMD+∠HMC=90°,∴∠AMH=90°,
∴∠MHA=45°,即α+β=45°.
延伸:∵∠MPH=90°,
∴MH为过M,P,H三点的圆的直径.
由勾股定理,得MH==.
∵∠MHR=45°,∴所对的圆心角为90°,
∴的长度为=.
【基础练习】
知识点1 弧长公式及其应用
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为 ( )
A.π B.2π C.3π D.6π
2.一个扇形的圆心角为60°,它的弧长为2πcm,则这个扇形的半径为 ( )
A.6cm B.12cm
C.2cm D.cm
3.一个扇形的半径为8cm,弧长为πcm,则这个扇形的圆心角为 ( )
A.60° B.120° C.150° D.180°
4.如图1,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=6,则的长为 ( )
图1
A. B. C.2π D.2π
5.如图2,将☉O沿弦AB折叠,使恰好经过圆心O,若的长为2π,则☉O的半径为 .
图2
6.制造弯形管道时,经常要先按中心线计算“展直长度”,再下料.图3是一段管道,其中∠O=∠O'=90°,中心线的两条弧的半径都是1000mm,求这段管道的展直长度.(π≈3.14)
图3
知识点2 扇形的面积公式及其应用
7.已知扇形的圆心角为120°,半径为3,则该扇形的面积为 ( )
A.2π B.3π C.6π D.12π
8.若一个扇形的半径是18cm,面积是54πcm2,则该扇形的圆心角为 ( )
A.30° B.60° C.90° D.120°
9.如图4,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以点A为圆心,AB长为半径的扇形(忽略铁丝的粗细),则所得扇形BAD的面积为 ( )
图4
A.6 B.7 C.8 D.9
10.[2020·山西]中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图5是某一摆盘的几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C,D两点之间的距离为4cm,圆心角为60°,则图中摆盘的面积是 ( )
图5
A.80πcm2 B.40πcm2
C.24πcm2 D.2πcm2
11.一个扇形的弧长是20πcm,面积是240πcm2,求这个扇形的半径和圆心角.
【能力提升】
12.如图6,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点O为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为 ( )
图6
A.- B.+
C.2-π D.4-
13.如图7,点A,B,C在☉O上,∠A=60°,∠C=70°,OB=9,则的长为 .
图7
14.如图8,C,D分别是半圆上的三等分点,若阴影部分的面积是π,则半圆的半径OA的长为 .
图8
15.如图9,在☉O中,OA=3cm,∠C=45°,则图中阴影部分的面积为 .
图9
16.一个滑轮起重装置如图10所示,滑轮的半径是10cm,当滑轮的一条半径OA绕轴心O按逆时针方向旋转120°时,重物上升 cm.(结果保留π)
图10
17.如图11,C为半圆内一点,O为圆心,直径AB为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B'OC'的位置,点C'在OA上,则边BC扫过区域(图中阴影部分)的面积为 cm2.
图11
18.如图12,AB为☉O的直径,C为☉O上一点,∠ABC的平分线交☉O于点D,DE⊥BC交BC的延长线于点E.
(1)试判断DE与☉O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3,DF=3,求图中阴影部分的面积.
图12
19.问题:已知α,β均为锐角,tanα=,tanβ=,求α+β的度数.
探究:用6个小正方形构造如图13所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;
延伸:设经过图中M,P,H三点的圆弧与AH交于点R,求的长度.
图13
答案
1.C
2.A [解析]根据弧长公式,得πr=2π,解得r=6.
3.B 4.B
5.3 [解析]连接OA,OB,过点O作OC⊥AB于点C,如图.
由题意得OC=OA.
则在Rt△OAC中,sin∠OAC==,
∴∠OAC=30°.
∵OA=OB,
∴∠OBA=∠OAC=30°,
∴∠AOB=120°.
设☉O的半径为r.
则的长为=2π,
∴r=3.
6.解:这段管道的展直长度为2×+3000=1000π+3000≈1000×3.14+3000=6140(mm).
7.B [解析]S扇形==3π.
8.B [解析]设扇形的圆心角为n°,则=54π,解得n=60.故选B.
9.D [解析]∵正方形的边长为3,
∴弧BD的长为6,
∴S扇形BAD=lr=×6×3=9.故选D.
10.B [解析]如图,连接CD.
∵OC=OD,∠O=60°,
∴△COD是等边三角形,
∴OC=OD=CD=4cm,
∴S阴影=S扇形OAB-S扇形OCD=-=40π(cm2).
故选B.
11.解:设这个扇形的半径为Rcm,圆心角为n°.
∵S扇形=lR,∴240π=×20π×R,
解得R=24.
∵l=,
∴20π=,解得n=150.
因此这个扇形的半径为24cm,圆心角为150°.
12.A
13.8π
14.3 [解析]如图,连接OC,OD,CD.
∵△COD和△BCD同底等高,
∴S△COD=S△BCD.
∴阴影部分的面积=S扇形OCD.
∵C,D为半圆的三等分点,
∴∠COD=180°÷3=60°.
又∵阴影部分的面积是π,
∴=π,
∴r=3.
15.π-cm2 [解析]∵∠C=45°,
∴∠AOB=90°.
∵OA=OB=3,
∴S阴影=S扇形OAB-S△OAB=-×3×3=-cm2.
16.π [解析]l==π(cm).
故答案为π.
17.π
18.解:(1)DE与☉O相切.理由:连接DO,如图.
∵DO=BO,
∴∠ODB=∠OBD.
∵∠ABC的平分线交☉O于点D,
∴∠EBD=∠OBD,
∴∠EBD=∠ODB,∴DO∥BE.
∵DE⊥BC,∴DO⊥DE.
又∵OD是☉O的半径,∴DE与☉O相切.
(2)∵∠ABC的平分线交☉O于点D,DE⊥BE,DF⊥AB,∴DE=DF=3.
∵BE=3,∴BD==6,
∴sin∠DBF==,∴∠DBF=30°,
∴∠DOF=60°,
∴sin60°===,cos60°==,
∴DO=2,FO=,
故图中阴影部分的面积为-×3=2π-.
19.解:探究:如图,连接AM,MH,则∠MHP=∠α.
∵AD=MC,∠D=∠C,MD=HC,
∴△ADM≌△MCH,
∴AM=MH,∠DAM=∠HMC.
∵∠AMD+∠DAM=90°,
∴∠AMD+∠HMC=90°,∴∠AMH=90°,
∴∠MHA=45°,即α+β=45°.
延伸:∵∠MPH=90°,
∴MH为过M,P,H三点的圆的直径.
由勾股定理,得MH==.
∵∠MHR=45°,∴所对的圆心角为90°,
∴的长度为=.
