2021-2022学年华东师大版八年级数学上册13.2《三角形全等的判定》期末复习测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册13.2《三角形全等的判定》期末复习测评(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 296.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 19:48:05 | ||
图片预览


文档简介
2021-2022学年华师大版八年级数学上册《三角形全等的判定》期末综合复习测评(附答案)
1.如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55° B.60° C.65° D.70°
2.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30° B.25° C.35° D.65°
3.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,BF=20,平移距离为6,则△OEC的面积为( )
A.24 B.40 C.42 D.48
4.根据下列已知条件,能画出唯一的△ABC的是( )
A.∠C=90°,AB=6 B.AB=4,BC=3,∠A=30°
C.∠A=60°,∠B=45°,AB=4 D.AB=3,BC=4,CA=8
5.打下列说法:①两个形状相同的图形称为全等图形;②边、角分别对应相等的两个多边形全等;③全等图形的形状、大小都相同;④面积相等的两个三角形全等.其中正确的是( )
A.①②③ B.①②④ C.①③ D.②③
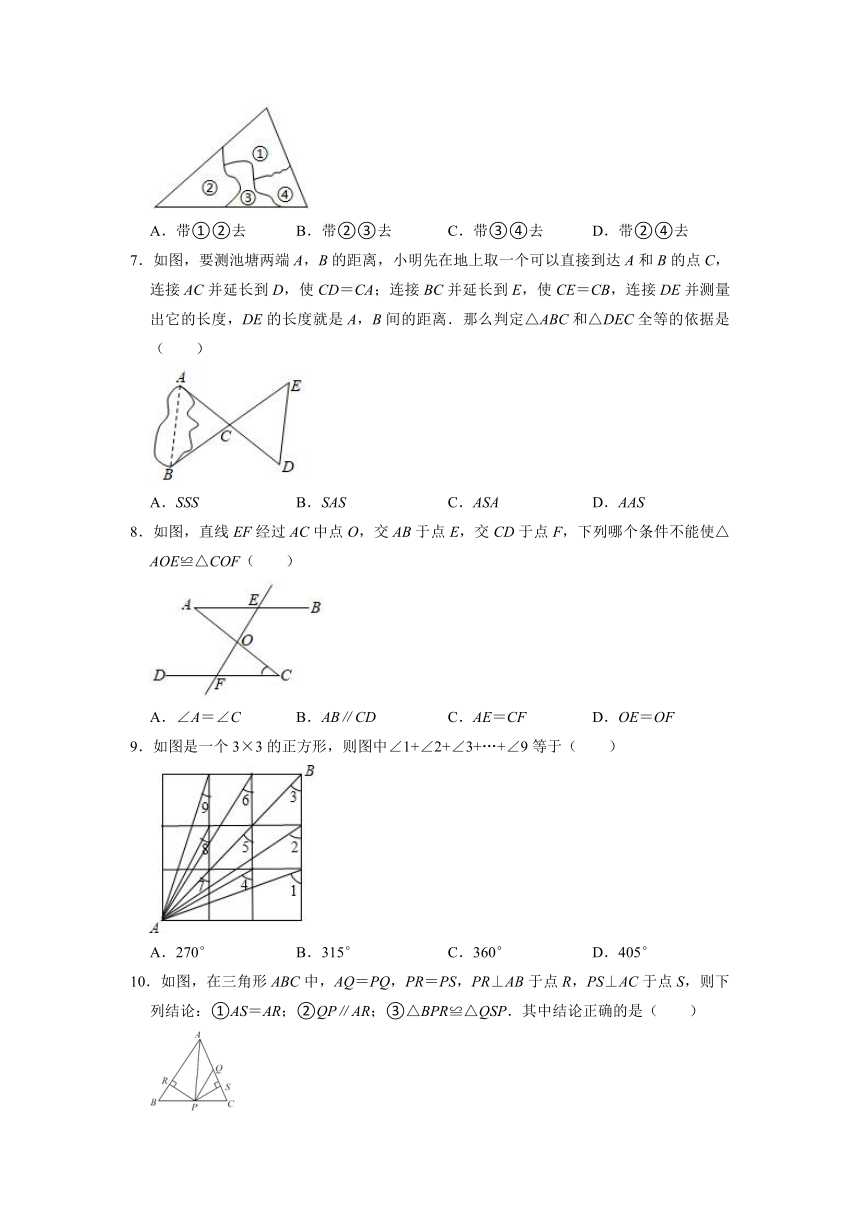
6.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A.带①②去 B.带②③去 C.带③④去 D.带②④去
7.如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离.那么判定△ABC和△DEC全等的依据是( )
A.SSS B.SAS C.ASA D.AAS
8.如图,直线EF经过AC中点O,交AB于点E,交CD于点F,下列哪个条件不能使△AOE≌△COF( )
A.∠A=∠C B.AB∥CD C.AE=CF D.OE=OF
9.如图是一个3×3的正方形,则图中∠1+∠2+∠3+…+∠9等于( )
A.270° B.315° C.360° D.405°
10.如图,在三角形ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①AS=AR;②QP∥AR;③△BPR≌△QSP.其中结论正确的是( )
A.①②③ B.①② C.① D.①③
二.填空题(共4小题,满分16分,每小题4分)
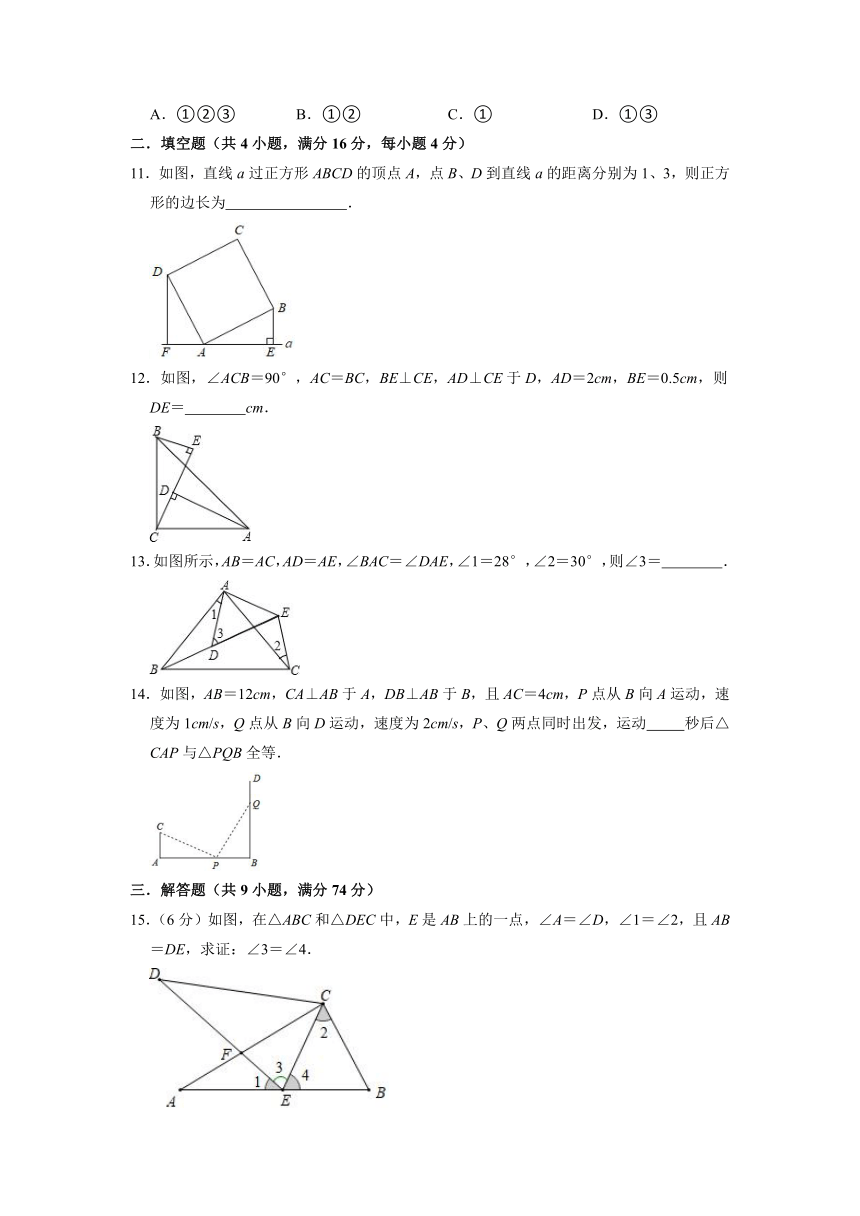
11.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为1、3,则正方形的边长为 .
12.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2cm,BE=0.5cm,则DE= cm.
13.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=28°,∠2=30°,则∠3= .
14.如图,AB=12cm,CA⊥AB于A,DB⊥AB于B,且AC=4cm,P点从B向A运动,速度为1cm/s,Q点从B向D运动,速度为2cm/s,P、Q两点同时出发,运动 秒后△CAP与△PQB全等.
三.解答题(共9小题,满分74分)
15.(6分)如图,在△ABC和△DEC中,E是AB上的一点,∠A=∠D,∠1=∠2,且AB=DE,求证:∠3=∠4.
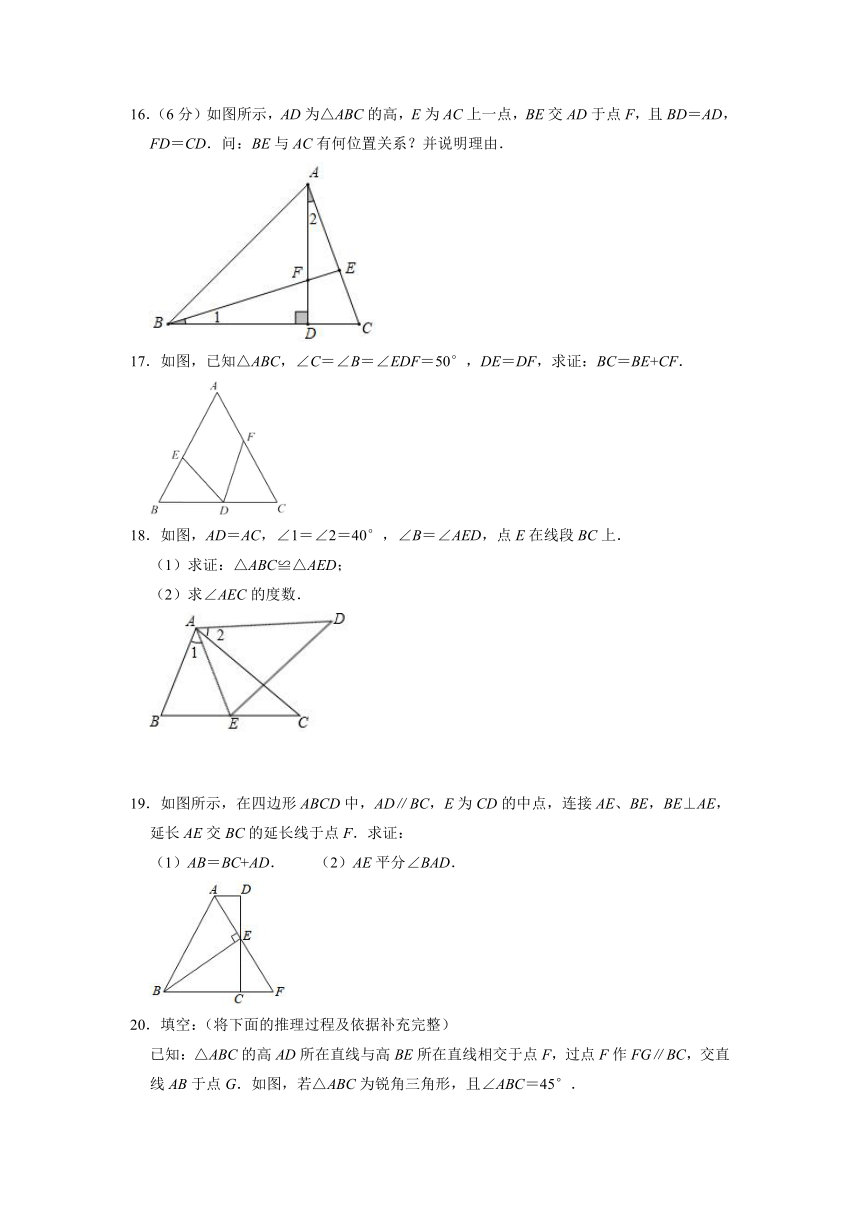
16.(6分)如图所示,AD为△ABC的高,E为AC上一点,BE交AD于点F,且BD=AD,FD=CD.问:BE与AC有何位置关系?并说明理由.
17.如图,已知△ABC,∠C=∠B=∠EDF=50°,DE=DF,求证:BC=BE+CF.
18.如图,AD=AC,∠1=∠2=40°,∠B=∠AED,点E在线段BC上.
(1)求证:△ABC≌△AED;
(2)求∠AEC的度数.
19.如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)AB=BC+AD. (2)AE平分∠BAD.
20.填空:(将下面的推理过程及依据补充完整)
已知:△ABC的高AD所在直线与高BE所在直线相交于点F,过点F作FG∥BC,交直线AB于点G.如图,若△ABC为锐角三角形,且∠ABC=45°.
求证:①△BDF≌△ADC;②FG+DC=AD;
①证明:∵AD,BE为高.
∴∠ADB=∠BEC=90°.
∵∠ABC=45°,
∴∠BAD=∠ =45°.
∴AD= .
∵∠BEC=90°,
∴∠CBE+∠C=90°( ).
又∵∠DAC+∠C=90°,
∴∠CBE=∠DAC( ).
在△FDB和△CDA中,.
∴△FDB≌△CDA( ).
②∵△FDB≌△CDA,
∴DF=DC( ).
∵GF∥BC,
∴∠AGF=∠ABC=45°( ).
∴∠AGF=∠ .
∴FA=FG.
∴FG+DC=FA+DF=AD.
21.如图,某地在山区修建高速公路时需挖通一条隧道,为估计这条隧道的长度需测出这座山A、B间的距离,结合所学知识或方法,设计测量方案你能给出什么好的方法吗?
22.如图,∠ABC=90°,FA⊥AB于点A,D是线段AB上的点,AD=BC,AF=BD.
(1)判断DF与DC的数量关系为 ,位置关系为 .
(2)如图2,若点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,试说明(1)中结论是否成立,并说明理由.
23.如图,大小不同的两块三角板△ABC和△DEC直角顶点重合在点C处,AC=BC,DC=EC,连接AE、BD,点A恰好在线段BD上.
(1)找出图中的全等三角形,并说明理由;
(2)当AD=AB=4cm,则AE的长度为 cm.
(3)猜想AE与BD的位置关系,并说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵,△ABC≌△EDC.
∴∠DCE=∠ACB=20°,∠BCD=∠ACE=90°,AC=CE,
∴∠ACD=90°﹣20°=70°,
∵点A,D,E在同一条直线上,
∴∠ADC+∠EDC=180°,
∵∠EDC+∠E+∠DCE=180°,
∴∠ADC=∠E+20°,
∵∠ACE=90°,AC=CE
∴∠DAC+∠E=90°,∠E=∠DAC=45°
在△ADC中,∠ADC+∠DAC+∠DCA=180°,
即45°+70°+∠ADC=180°,
解得:∠ADC=65°,
故选:C.
2.解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°﹣65°=25°,
故选:B.
3.解:由平移的性质知,BE=CF=6,DE=AB=10,BF=20
∴OE=DE﹣DO=10﹣4=6,EC=20﹣6﹣6=8,
∴△OEC的面积=×6×8=24.
故选:A.
4.解:A.如图Rt△ACB和Rt△ADB的斜边都是AB,但是两三角形不全等,故本选项不符合题意;
B.AB=4,BC=3,∠A=30°,不符合全等三角形的判定定理,不能画出唯一的三角形,故本选项不符合题意;
C.∠A=60°,∠B=45°,AB=4,符合全等三角形的判定定理ASA,能画出唯一的三角形,故本选项符合题意;
D.3+4<8,不符合三角形的三边关系定理,不能画出三角形,故本选项不符合题意;
故选:C.
5.解:两个形状相同、大小也相同的图形称为全等图形,故①错误;
边、角分别对应相等的两个多边形全等,故②正确;
全等图形的形状、大小都相同,故③正确;
如图,△ABC和△DEF中,BC=2,EF=1,高AN=1,高DM=2,
△ABC和△DEF的面积都是=1,
当时两三角形不全等,
即面积相等的两个三角形不一定全等,故④错误;
即正确的为②③,
故选:D.
6.解:A、带①②去,符合ASA判定,选项符合题意;
B、带②③去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
C、带③④去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
D、带②④去,仅保留了原三角形的两个角和部分边,不符合任何判定方法,选项不符合题意;
故选:A.
7.解:由题意知CD=CA,CE=CB,
在△DCE和△ABC中,
,
∴△DCE≌△ABC(SAS).
故选:B.
8.解:由题意可得,
AO=CO,∠AOE=∠COF,
当添加条件∠A=∠C时,△AOE≌△COF(ASA),故选项A不符合题意;
当添加条件AB∥CD时,则∠A=∠C,△AOE≌△COF(ASA),故选项B不符合题意;
当添加条件AE=CF时,无法判断△AOE≌△COF,故选项C符合题意;
当添加条件OE=OF时,△AOE≌△COF(SAS),故选项D不符合题意;
故选:C.
9.解:根据正方形和全等三角形的知识可知:相对应的三角形是全等的,如∠1与∠9所在的两个三角形全等,
则角之间的关系为:∠1+∠9=90°,∠2+∠6=90°,∠4+∠8=90°,∠3=∠5=∠7=45°,
∴∠1+∠2+∠3+…+∠9=405°.
故选:D.
10.解:∵PR=PS,PR⊥AB于R,PS⊥AC于S,
∴点P在∠A的平分线上;AQ=PQ,
①正确,∵点P在∠A的平分线上,
∴△ARP≌△ASP(AAS).
∴AS=AR.
②正确,∵点P在∠A的平分线上;
∴∠2=∠3.
又∵AQ=PQ,
∴∠1=∠2.
∴∠1=∠3.
∴QP∥AR.
③错误,∵△ABC不一定为等边三角形,
不能得出∠B=∠C.
又∵PR⊥AB于R,PS⊥AC于S,
∴∠BRP=∠CSP.
不能得出△BRP≌△QSP.
故选:B.
二.填空题(共4小题,满分16分,每小题4分)
11.解:在正方形ABCD中,AD=AB,
∵DF⊥AF,BE⊥AE,
∴∠AFD=∠AEB=90°,∠ADF+∠DAF=90°,
∵∠DAF+∠BAE=90°,
∴∠ADF=∠BAE,
在Rt△AFD和Rt△BEA中,
,
∴Rt△AFD≌Rt△BEA(AAS),
∴DF=AE=3,AF=BE=1,
在Rt△BEA中,由勾股定理得:
AB=.
故答案为:.
12.解:∵BE⊥CE,AD⊥CE
∴∠E=∠ADC=90°
∴∠DAC+∠DCA=90°
∵∠ACB=90°
∴∠BCE+∠DCA=90°
∴∠DAC=∠BCE
在△ACD和△CBE中,
,
∴△ACD≌△CBE
∴BE=CD=0.5(cm),EC=AD=2(cm)
DE=CE﹣CD=1.5(cm),
故答案为1.5
13.解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠2=∠ABD=30°,
∵∠1=28°,
∴∠3=∠1+∠ABD=28°+30°=58°,
故答案为:58°.
14.解:当△CPA≌△PQB时,BP=AC=4(cm),
则BQ=AP=AB﹣BP=12﹣4=8(cm),
A的运动时间是:4÷1=4(秒),
Q的运动时间是:8÷2=4(秒),
则当t=4秒时,两个三角形全等;
当△CPA≌△PQB时,BQ=AC=4(cm),
AP=BP=AB=6(cm),
则P运动的时间是:6÷1=6(秒),
Q运动的时间是:4÷2=2(秒),
故不能成立.
综上所述,运动4秒后,△CPA与△PQB全等.
故答案为:4.
三.解答题(共9小题,满分74分)
15.证明:∵∠2+∠4+∠B=180°,∠1+∠3+∠4=180°,∠1=∠2,
∴∠3=∠B,
在△ABC与△DEC中,
,
∴△ABC≌△DEC(ASA),
∴CE=BC,
∴∠4=∠B,
∴∠3=∠4.
16.解:BE⊥AC,理由如下:
在△BDF和△ADC中,
,
∴△BDF≌△ADC(SAS),
∴∠DAC=∠DBF,
∵∠DAC+∠C=90°,
∴∠DBF+∠C=90°,
∴∠BEC=90°,
∴BE⊥AC.
17.证明:∵∠C=∠B=∠EDF=50°,
∵∠BED+∠EDB+∠B=∠FDC+∠EDF+∠EDB=180°,
∴∠BED=∠FDC,
在△BED与△CDF中,
,
∴△BED≌△CDF(AAS),
∴BD=CF,CD=BE,
∴BC=BD+DC=BE+CF.
18.(1)证明:∵∠1=∠2=40°,
∴∠1+∠CAE=∠2+∠CAE,
即∠BAC=∠EAD,
在△ABC和△AED中,
,
∴△ABC≌△AED(AAS).
(2)解:由(1)得:△ABC≌△AED.
∴AB=AE,
∴∠B=∠AEB=(180°﹣∠1)=(180°﹣40°)=70°,
∴∠AEC=∠1+∠B=40°+70°=110°.
19.证明:(1)∵AD∥BC,
∴∠D=∠ECF.
∵∠AED与∠FEC是对顶角,
∴∠AED=∠FEC.
∵E为CD的中点,
∴DE=CE.
在△AED和△FEC中,
,
∴△AED≌△FEC(ASA).
∴AD=CF,AE=FE.
∵BE⊥AE于点E,
∴∠AEB=90°,∠FEB=90°.
∴∠AEB=∠FEB.
在△AEB和△FEB中,
,
∴△AEB≌△FEB(SAS).
∴AB=BF.
∴AB=BC+CF.
∴AB=BC+AD.
(2)由(1)得:△AEB≌△FEB,△AED≌△FEC.
∴∠BAE=∠F,∠DAE=∠F.
∴∠BAE=∠DAE.
∴AE平分∠BAD.
20.①证明:∵AD,BE为高.
∴∠ADB=∠BEC=90°.
∵∠ABC=45°,
∴∠BAD=∠ABD=45°.
∴AD=BD.
∵∠BEC=90°,
∴∠CBE+∠C=90°(三角形的内角和定理).
又∵∠DAC+∠C=90°,
∴∠CBE=∠DAC(同角的余角相等).
在△FDB和△CDA中,
.
∴△FDB≌△CDA(ASA).
②∵△FDB≌△CDA,
∴DF=DC(全等三角形的对应边相等).
∵GF∥BC,
∴∠AGF=∠ABC=45°(两直线平行,同位角相等).
∴∠AGF=∠FAG.
∴FA=FG.
∴FG+DC=FA+DF=AD,
故答案为:ABD,BD,三角形的内角和定理,同角的余角相等,ASA,全等三角形的对应边相等,两直线平行,同位角相等,FAG.
21.解:选择一合适的地点O,连接AO、BO,测出AO和BO的长度,延长AO、BO至A′、B′,使OA′=OA,OB′=OB,连接A′B′,这样就构成两个三角形,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS),
∴AB=A′B′.
22.解:(1)DF=CD,CD⊥DF,理由如下:
∵FA⊥AB,
∴∠DAF=90°=∠CBD,
在△ADF和△BCD中,
,
∴△ADF≌△BCD(SAS),
∴DF=DC,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,
∴∠CDF=90°,
∴DF⊥DC;
(2)成立,理由如下:
∵FA⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中,
,
∴△ADF≌△BCD(SAS),
∴DF=DC,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,
即∠CDF=90°,
∴DF⊥DC.
23.解:(1)△CBD≌△CAE,理由如下:
∵∠ACB=∠DCE=90°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△CBD与△CAE中,
,
∴△CBD≌△CAE(SAS);
(2)∵△CBD≌△CAE,
∴BD=AE=AD+AB=4+4=8(cm),
故答案为:8;
(3)AE⊥BD,理由如下:
AE与CD相交于点O,在△AOD与△COE中,
∵△CBD≌△CAE,
∴∠ADO=∠CEO,
∵∠AOD=∠COE,
∴∠OAD=∠OCE=90°,
∴AE⊥BD.
1.如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55° B.60° C.65° D.70°
2.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30° B.25° C.35° D.65°
3.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,BF=20,平移距离为6,则△OEC的面积为( )
A.24 B.40 C.42 D.48
4.根据下列已知条件,能画出唯一的△ABC的是( )
A.∠C=90°,AB=6 B.AB=4,BC=3,∠A=30°
C.∠A=60°,∠B=45°,AB=4 D.AB=3,BC=4,CA=8
5.打下列说法:①两个形状相同的图形称为全等图形;②边、角分别对应相等的两个多边形全等;③全等图形的形状、大小都相同;④面积相等的两个三角形全等.其中正确的是( )
A.①②③ B.①②④ C.①③ D.②③
6.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A.带①②去 B.带②③去 C.带③④去 D.带②④去
7.如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A,B间的距离.那么判定△ABC和△DEC全等的依据是( )
A.SSS B.SAS C.ASA D.AAS
8.如图,直线EF经过AC中点O,交AB于点E,交CD于点F,下列哪个条件不能使△AOE≌△COF( )
A.∠A=∠C B.AB∥CD C.AE=CF D.OE=OF
9.如图是一个3×3的正方形,则图中∠1+∠2+∠3+…+∠9等于( )
A.270° B.315° C.360° D.405°
10.如图,在三角形ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①AS=AR;②QP∥AR;③△BPR≌△QSP.其中结论正确的是( )
A.①②③ B.①② C.① D.①③
二.填空题(共4小题,满分16分,每小题4分)
11.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为1、3,则正方形的边长为 .
12.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2cm,BE=0.5cm,则DE= cm.
13.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=28°,∠2=30°,则∠3= .
14.如图,AB=12cm,CA⊥AB于A,DB⊥AB于B,且AC=4cm,P点从B向A运动,速度为1cm/s,Q点从B向D运动,速度为2cm/s,P、Q两点同时出发,运动 秒后△CAP与△PQB全等.
三.解答题(共9小题,满分74分)
15.(6分)如图,在△ABC和△DEC中,E是AB上的一点,∠A=∠D,∠1=∠2,且AB=DE,求证:∠3=∠4.
16.(6分)如图所示,AD为△ABC的高,E为AC上一点,BE交AD于点F,且BD=AD,FD=CD.问:BE与AC有何位置关系?并说明理由.
17.如图,已知△ABC,∠C=∠B=∠EDF=50°,DE=DF,求证:BC=BE+CF.
18.如图,AD=AC,∠1=∠2=40°,∠B=∠AED,点E在线段BC上.
(1)求证:△ABC≌△AED;
(2)求∠AEC的度数.
19.如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)AB=BC+AD. (2)AE平分∠BAD.
20.填空:(将下面的推理过程及依据补充完整)
已知:△ABC的高AD所在直线与高BE所在直线相交于点F,过点F作FG∥BC,交直线AB于点G.如图,若△ABC为锐角三角形,且∠ABC=45°.
求证:①△BDF≌△ADC;②FG+DC=AD;
①证明:∵AD,BE为高.
∴∠ADB=∠BEC=90°.
∵∠ABC=45°,
∴∠BAD=∠ =45°.
∴AD= .
∵∠BEC=90°,
∴∠CBE+∠C=90°( ).
又∵∠DAC+∠C=90°,
∴∠CBE=∠DAC( ).
在△FDB和△CDA中,.
∴△FDB≌△CDA( ).
②∵△FDB≌△CDA,
∴DF=DC( ).
∵GF∥BC,
∴∠AGF=∠ABC=45°( ).
∴∠AGF=∠ .
∴FA=FG.
∴FG+DC=FA+DF=AD.
21.如图,某地在山区修建高速公路时需挖通一条隧道,为估计这条隧道的长度需测出这座山A、B间的距离,结合所学知识或方法,设计测量方案你能给出什么好的方法吗?
22.如图,∠ABC=90°,FA⊥AB于点A,D是线段AB上的点,AD=BC,AF=BD.
(1)判断DF与DC的数量关系为 ,位置关系为 .
(2)如图2,若点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,试说明(1)中结论是否成立,并说明理由.
23.如图,大小不同的两块三角板△ABC和△DEC直角顶点重合在点C处,AC=BC,DC=EC,连接AE、BD,点A恰好在线段BD上.
(1)找出图中的全等三角形,并说明理由;
(2)当AD=AB=4cm,则AE的长度为 cm.
(3)猜想AE与BD的位置关系,并说明理由.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵,△ABC≌△EDC.
∴∠DCE=∠ACB=20°,∠BCD=∠ACE=90°,AC=CE,
∴∠ACD=90°﹣20°=70°,
∵点A,D,E在同一条直线上,
∴∠ADC+∠EDC=180°,
∵∠EDC+∠E+∠DCE=180°,
∴∠ADC=∠E+20°,
∵∠ACE=90°,AC=CE
∴∠DAC+∠E=90°,∠E=∠DAC=45°
在△ADC中,∠ADC+∠DAC+∠DCA=180°,
即45°+70°+∠ADC=180°,
解得:∠ADC=65°,
故选:C.
2.解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°﹣65°=25°,
故选:B.
3.解:由平移的性质知,BE=CF=6,DE=AB=10,BF=20
∴OE=DE﹣DO=10﹣4=6,EC=20﹣6﹣6=8,
∴△OEC的面积=×6×8=24.
故选:A.
4.解:A.如图Rt△ACB和Rt△ADB的斜边都是AB,但是两三角形不全等,故本选项不符合题意;
B.AB=4,BC=3,∠A=30°,不符合全等三角形的判定定理,不能画出唯一的三角形,故本选项不符合题意;
C.∠A=60°,∠B=45°,AB=4,符合全等三角形的判定定理ASA,能画出唯一的三角形,故本选项符合题意;
D.3+4<8,不符合三角形的三边关系定理,不能画出三角形,故本选项不符合题意;
故选:C.
5.解:两个形状相同、大小也相同的图形称为全等图形,故①错误;
边、角分别对应相等的两个多边形全等,故②正确;
全等图形的形状、大小都相同,故③正确;
如图,△ABC和△DEF中,BC=2,EF=1,高AN=1,高DM=2,
△ABC和△DEF的面积都是=1,
当时两三角形不全等,
即面积相等的两个三角形不一定全等,故④错误;
即正确的为②③,
故选:D.
6.解:A、带①②去,符合ASA判定,选项符合题意;
B、带②③去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
C、带③④去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
D、带②④去,仅保留了原三角形的两个角和部分边,不符合任何判定方法,选项不符合题意;
故选:A.
7.解:由题意知CD=CA,CE=CB,
在△DCE和△ABC中,
,
∴△DCE≌△ABC(SAS).
故选:B.
8.解:由题意可得,
AO=CO,∠AOE=∠COF,
当添加条件∠A=∠C时,△AOE≌△COF(ASA),故选项A不符合题意;
当添加条件AB∥CD时,则∠A=∠C,△AOE≌△COF(ASA),故选项B不符合题意;
当添加条件AE=CF时,无法判断△AOE≌△COF,故选项C符合题意;
当添加条件OE=OF时,△AOE≌△COF(SAS),故选项D不符合题意;
故选:C.
9.解:根据正方形和全等三角形的知识可知:相对应的三角形是全等的,如∠1与∠9所在的两个三角形全等,
则角之间的关系为:∠1+∠9=90°,∠2+∠6=90°,∠4+∠8=90°,∠3=∠5=∠7=45°,
∴∠1+∠2+∠3+…+∠9=405°.
故选:D.
10.解:∵PR=PS,PR⊥AB于R,PS⊥AC于S,
∴点P在∠A的平分线上;AQ=PQ,
①正确,∵点P在∠A的平分线上,
∴△ARP≌△ASP(AAS).
∴AS=AR.
②正确,∵点P在∠A的平分线上;
∴∠2=∠3.
又∵AQ=PQ,
∴∠1=∠2.
∴∠1=∠3.
∴QP∥AR.
③错误,∵△ABC不一定为等边三角形,
不能得出∠B=∠C.
又∵PR⊥AB于R,PS⊥AC于S,
∴∠BRP=∠CSP.
不能得出△BRP≌△QSP.
故选:B.
二.填空题(共4小题,满分16分,每小题4分)
11.解:在正方形ABCD中,AD=AB,
∵DF⊥AF,BE⊥AE,
∴∠AFD=∠AEB=90°,∠ADF+∠DAF=90°,
∵∠DAF+∠BAE=90°,
∴∠ADF=∠BAE,
在Rt△AFD和Rt△BEA中,
,
∴Rt△AFD≌Rt△BEA(AAS),
∴DF=AE=3,AF=BE=1,
在Rt△BEA中,由勾股定理得:
AB=.
故答案为:.
12.解:∵BE⊥CE,AD⊥CE
∴∠E=∠ADC=90°
∴∠DAC+∠DCA=90°
∵∠ACB=90°
∴∠BCE+∠DCA=90°
∴∠DAC=∠BCE
在△ACD和△CBE中,
,
∴△ACD≌△CBE
∴BE=CD=0.5(cm),EC=AD=2(cm)
DE=CE﹣CD=1.5(cm),
故答案为1.5
13.解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠2=∠ABD=30°,
∵∠1=28°,
∴∠3=∠1+∠ABD=28°+30°=58°,
故答案为:58°.
14.解:当△CPA≌△PQB时,BP=AC=4(cm),
则BQ=AP=AB﹣BP=12﹣4=8(cm),
A的运动时间是:4÷1=4(秒),
Q的运动时间是:8÷2=4(秒),
则当t=4秒时,两个三角形全等;
当△CPA≌△PQB时,BQ=AC=4(cm),
AP=BP=AB=6(cm),
则P运动的时间是:6÷1=6(秒),
Q运动的时间是:4÷2=2(秒),
故不能成立.
综上所述,运动4秒后,△CPA与△PQB全等.
故答案为:4.
三.解答题(共9小题,满分74分)
15.证明:∵∠2+∠4+∠B=180°,∠1+∠3+∠4=180°,∠1=∠2,
∴∠3=∠B,
在△ABC与△DEC中,
,
∴△ABC≌△DEC(ASA),
∴CE=BC,
∴∠4=∠B,
∴∠3=∠4.
16.解:BE⊥AC,理由如下:
在△BDF和△ADC中,
,
∴△BDF≌△ADC(SAS),
∴∠DAC=∠DBF,
∵∠DAC+∠C=90°,
∴∠DBF+∠C=90°,
∴∠BEC=90°,
∴BE⊥AC.
17.证明:∵∠C=∠B=∠EDF=50°,
∵∠BED+∠EDB+∠B=∠FDC+∠EDF+∠EDB=180°,
∴∠BED=∠FDC,
在△BED与△CDF中,
,
∴△BED≌△CDF(AAS),
∴BD=CF,CD=BE,
∴BC=BD+DC=BE+CF.
18.(1)证明:∵∠1=∠2=40°,
∴∠1+∠CAE=∠2+∠CAE,
即∠BAC=∠EAD,
在△ABC和△AED中,
,
∴△ABC≌△AED(AAS).
(2)解:由(1)得:△ABC≌△AED.
∴AB=AE,
∴∠B=∠AEB=(180°﹣∠1)=(180°﹣40°)=70°,
∴∠AEC=∠1+∠B=40°+70°=110°.
19.证明:(1)∵AD∥BC,
∴∠D=∠ECF.
∵∠AED与∠FEC是对顶角,
∴∠AED=∠FEC.
∵E为CD的中点,
∴DE=CE.
在△AED和△FEC中,
,
∴△AED≌△FEC(ASA).
∴AD=CF,AE=FE.
∵BE⊥AE于点E,
∴∠AEB=90°,∠FEB=90°.
∴∠AEB=∠FEB.
在△AEB和△FEB中,
,
∴△AEB≌△FEB(SAS).
∴AB=BF.
∴AB=BC+CF.
∴AB=BC+AD.
(2)由(1)得:△AEB≌△FEB,△AED≌△FEC.
∴∠BAE=∠F,∠DAE=∠F.
∴∠BAE=∠DAE.
∴AE平分∠BAD.
20.①证明:∵AD,BE为高.
∴∠ADB=∠BEC=90°.
∵∠ABC=45°,
∴∠BAD=∠ABD=45°.
∴AD=BD.
∵∠BEC=90°,
∴∠CBE+∠C=90°(三角形的内角和定理).
又∵∠DAC+∠C=90°,
∴∠CBE=∠DAC(同角的余角相等).
在△FDB和△CDA中,
.
∴△FDB≌△CDA(ASA).
②∵△FDB≌△CDA,
∴DF=DC(全等三角形的对应边相等).
∵GF∥BC,
∴∠AGF=∠ABC=45°(两直线平行,同位角相等).
∴∠AGF=∠FAG.
∴FA=FG.
∴FG+DC=FA+DF=AD,
故答案为:ABD,BD,三角形的内角和定理,同角的余角相等,ASA,全等三角形的对应边相等,两直线平行,同位角相等,FAG.
21.解:选择一合适的地点O,连接AO、BO,测出AO和BO的长度,延长AO、BO至A′、B′,使OA′=OA,OB′=OB,连接A′B′,这样就构成两个三角形,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS),
∴AB=A′B′.
22.解:(1)DF=CD,CD⊥DF,理由如下:
∵FA⊥AB,
∴∠DAF=90°=∠CBD,
在△ADF和△BCD中,
,
∴△ADF≌△BCD(SAS),
∴DF=DC,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,
∴∠CDF=90°,
∴DF⊥DC;
(2)成立,理由如下:
∵FA⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中,
,
∴△ADF≌△BCD(SAS),
∴DF=DC,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,
即∠CDF=90°,
∴DF⊥DC.
23.解:(1)△CBD≌△CAE,理由如下:
∵∠ACB=∠DCE=90°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△CBD与△CAE中,
,
∴△CBD≌△CAE(SAS);
(2)∵△CBD≌△CAE,
∴BD=AE=AD+AB=4+4=8(cm),
故答案为:8;
(3)AE⊥BD,理由如下:
AE与CD相交于点O,在△AOD与△COE中,
∵△CBD≌△CAE,
∴∠ADO=∠CEO,
∵∠AOD=∠COE,
∴∠OAD=∠OCE=90°,
∴AE⊥BD.
