北师大版6.2整理和复习(二)(课件)数学六年级下册(共16张PPT)
文档属性
| 名称 | 北师大版6.2整理和复习(二)(课件)数学六年级下册(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 09:54:38 | ||
图片预览






文档简介
(共16张PPT)
六年级下册
6.2整理和复习(二)
学习目标
1、在练习中,经历对比例、正、反比例、图形的移动的有关知识系统复习与整理的过程。
2、进一步理解并掌握比例、正、反比例、图形的移动的有关知识,能用比例、正、反比例、图形的移动的有关知识解决实际问题。
3、培养回顾与复习的好习惯,查漏补缺,获得积极的学习体验。
知识梳理
1、表示两个比相等的式子叫作( )。
2、判断了两个比是否成比例,看看这两个比的比值是否( )。
3、在比例里,两个外项的积等于两个( )的积。
4、解比例的依据是( )。
5、一幅图的图上距离和实际距离的比,叫作这幅图的( )。
比例
相等
内项
比例的基本性质
比例尺
知识梳理
6、( )∶( )=比例尺
7、比例尺还可以用( )表示。
8、稍复杂的图形的旋转时,可以先旋转关键( ),再确定图形的( )。可以剪一个同样大的图形( )一下,摆一摆。
9、平移时,关键要数清( ),找好对应的( ),再画出相应的图形。
图上距离
实际距离
线段
线段
位置
旋转
移动的格子数
关键点
典例精析:
1、比例和比例尺。
例:学校要修建一个长方体水池,在比例尺是1:200的设计图上,水池的长为12厘米,宽为10厘米,深为2厘米。
(1)按图施工,这个水池的长、宽、深各应挖多少米?
题型归纳
答:这个水池的长应挖24米。
答:这个水池的宽应挖20米。
答:这个水池的高应挖4米。
典例精析:
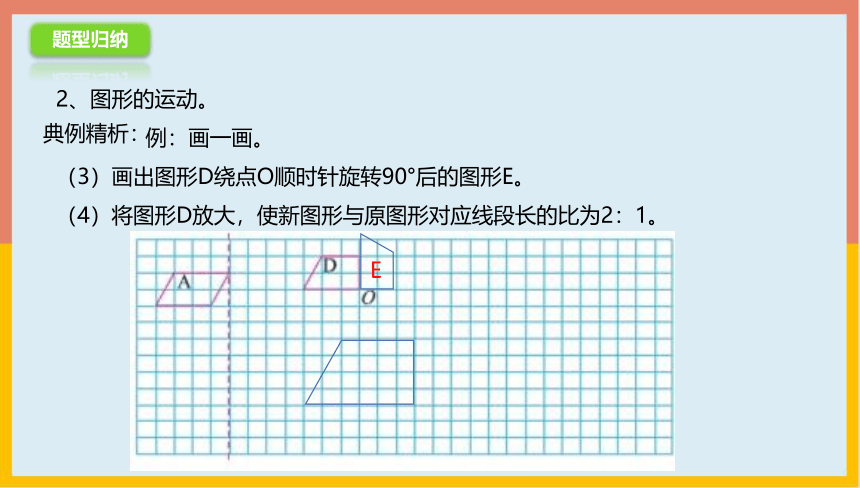
2、图形的运动。
例:画一画。
(1)图形A向下平移4格得到图形B。(2)以图中的虚线为对称轴,画出与图形B轴对称的图形C。
题型归纳
B
c
典例精析:
2、图形的运动。
例:画一画。
(3)画出图形D绕点O顺时针旋转90°后的图形E。
(4)将图形D放大,使新图形与原图形对应线段长的比为2:1。
题型归纳
E
典例精析:
3、正、反比例
例:下面各题中,那两个量成正比例,哪两个量成正比例?
(1)路程一定,时间与速度。
(2)圆锥的高一定,它的体积和底面积。
(3)做20道计算题,做对的题数和做错的题数。
题型归纳
成反比例
成正比例
不成比例
本课小结
A
判断了两个比是否成比例,看看这两个比的比值是否相等。一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
B
图形旋转时要先确定中心点,和旋转方向与角度。
C
两种量,一种量可以随着另一个种量的变化而变化。如果它们的比值一定,我们就说这两种量成正比例。如果它们的积一定,我们就说这两种量成反比例。
整理与复习(二)
1、把中间的长方形分别按比缩小和放大后得到了左、右两个长方形,请分别写出两个比例,并求出未知数x和y。
随堂检测
12:x=18:12
x=8
Y:18=18:12
y=27
2、解方程:
5:0.4=6:x
随堂检测
x=0.48
x=0.6
x=9.6
随堂检测
3、把24块巧克力糖平均分给小朋友,将每人分到糖的数量填在下面的表格中。
参与分糖的人数与每人分到糖的数量之间有什么关系?
3
4
2
12
8
24
参与分糖的人数与每人分到糖的数量成反比例关系。
随堂检测
4、某商场全部商品八折出售。
(1)完成下表。
(2)完成下图。
(3)如果用x表示原价,y表示现价,
那么y=( )。现价与原价是否成正比例?
为什么?
8
16
24
32
40
0.8x
成正比例 因为现价与原价的比值一定。
随堂检测
4、观察下图,回答问题。
(1)图形A经过怎样的运动能使图1变成图2?
(2)图形A经过怎样的运动能使图1变成图3?
图1中的图A先向右平移3格,再向下平移2格得到图2。
图1中的图A先绕右下方的顶点顺时针旋转90°,再向下平移1格得到图3。
作业布置
1、 下面每题中两种量是不是成比例?为什么?
(1)苹果的单价一定,购买苹果的数量与总价。
(2)长方体的体积一定,它的底面积与高。
(3)小刚放学,已经走的路程与剩下的路程。
2、预习第63、64页的有关内容。
空白演示
单击输入您的封面副标题
谢 谢 聆 听
六年级下册
6.2整理和复习(二)
学习目标
1、在练习中,经历对比例、正、反比例、图形的移动的有关知识系统复习与整理的过程。
2、进一步理解并掌握比例、正、反比例、图形的移动的有关知识,能用比例、正、反比例、图形的移动的有关知识解决实际问题。
3、培养回顾与复习的好习惯,查漏补缺,获得积极的学习体验。
知识梳理
1、表示两个比相等的式子叫作( )。
2、判断了两个比是否成比例,看看这两个比的比值是否( )。
3、在比例里,两个外项的积等于两个( )的积。
4、解比例的依据是( )。
5、一幅图的图上距离和实际距离的比,叫作这幅图的( )。
比例
相等
内项
比例的基本性质
比例尺
知识梳理
6、( )∶( )=比例尺
7、比例尺还可以用( )表示。
8、稍复杂的图形的旋转时,可以先旋转关键( ),再确定图形的( )。可以剪一个同样大的图形( )一下,摆一摆。
9、平移时,关键要数清( ),找好对应的( ),再画出相应的图形。
图上距离
实际距离
线段
线段
位置
旋转
移动的格子数
关键点
典例精析:
1、比例和比例尺。
例:学校要修建一个长方体水池,在比例尺是1:200的设计图上,水池的长为12厘米,宽为10厘米,深为2厘米。
(1)按图施工,这个水池的长、宽、深各应挖多少米?
题型归纳
答:这个水池的长应挖24米。
答:这个水池的宽应挖20米。
答:这个水池的高应挖4米。
典例精析:
2、图形的运动。
例:画一画。
(1)图形A向下平移4格得到图形B。(2)以图中的虚线为对称轴,画出与图形B轴对称的图形C。
题型归纳
B
c
典例精析:
2、图形的运动。
例:画一画。
(3)画出图形D绕点O顺时针旋转90°后的图形E。
(4)将图形D放大,使新图形与原图形对应线段长的比为2:1。
题型归纳
E
典例精析:
3、正、反比例
例:下面各题中,那两个量成正比例,哪两个量成正比例?
(1)路程一定,时间与速度。
(2)圆锥的高一定,它的体积和底面积。
(3)做20道计算题,做对的题数和做错的题数。
题型归纳
成反比例
成正比例
不成比例
本课小结
A
判断了两个比是否成比例,看看这两个比的比值是否相等。一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
B
图形旋转时要先确定中心点,和旋转方向与角度。
C
两种量,一种量可以随着另一个种量的变化而变化。如果它们的比值一定,我们就说这两种量成正比例。如果它们的积一定,我们就说这两种量成反比例。
整理与复习(二)
1、把中间的长方形分别按比缩小和放大后得到了左、右两个长方形,请分别写出两个比例,并求出未知数x和y。
随堂检测
12:x=18:12
x=8
Y:18=18:12
y=27
2、解方程:
5:0.4=6:x
随堂检测
x=0.48
x=0.6
x=9.6
随堂检测
3、把24块巧克力糖平均分给小朋友,将每人分到糖的数量填在下面的表格中。
参与分糖的人数与每人分到糖的数量之间有什么关系?
3
4
2
12
8
24
参与分糖的人数与每人分到糖的数量成反比例关系。
随堂检测
4、某商场全部商品八折出售。
(1)完成下表。
(2)完成下图。
(3)如果用x表示原价,y表示现价,
那么y=( )。现价与原价是否成正比例?
为什么?
8
16
24
32
40
0.8x
成正比例 因为现价与原价的比值一定。
随堂检测
4、观察下图,回答问题。
(1)图形A经过怎样的运动能使图1变成图2?
(2)图形A经过怎样的运动能使图1变成图3?
图1中的图A先向右平移3格,再向下平移2格得到图2。
图1中的图A先绕右下方的顶点顺时针旋转90°,再向下平移1格得到图3。
作业布置
1、 下面每题中两种量是不是成比例?为什么?
(1)苹果的单价一定,购买苹果的数量与总价。
(2)长方体的体积一定,它的底面积与高。
(3)小刚放学,已经走的路程与剩下的路程。
2、预习第63、64页的有关内容。
空白演示
单击输入您的封面副标题
谢 谢 聆 听
