2021-2022学年度沪科版数学七年级上册 3.3加减消元法解二元一次方程组 课件(19张)
文档属性
| 名称 | 2021-2022学年度沪科版数学七年级上册 3.3加减消元法解二元一次方程组 课件(19张) |  | |
| 格式 | ppt | ||
| 文件大小 | 978.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 19:55:14 | ||
图片预览






文档简介
(共19张PPT)
y = 2 x – 1
3 x – 4 y = 2
(1)
(2)
x – y = 5
2 x + 4 y = 1
(3)
3 x = 5 y
2 x – 7 y = 3
(4)
3x + 5 y = 21
2x - 5 y = -11
用学过的方法解下列,想一想
还有其它的方法吗?方程组
和
互为相反数……
按照这种思路,你能消去
一个未知数吗?
?
(3x + 5y)+(2x - 5y)=21 + (-11)
分析:
3X+5y +2x - 5y=10
①左边 + ② 左边 = ① 右边 + ②右边
5x+0y =10
5x=10
解方程组
3x + 5y = 5
3x - 4y =23
①
②
解:
把 ① - ② 得
9y = -18
y = - 2
把 y = - 2 代入 ① , 得
3x + 5 × ( - 2 ) = 5
解得
x = 5
所以原方程组的解是
x = 5
y = - 2
当二元一次方程组中两个方程的某个未知数的系数互为相反数或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,进而求出二元一次方程组的解。
加减消元法
像这样,通过对方程组中的两个方程进行加或减的运算就可以消去一个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.
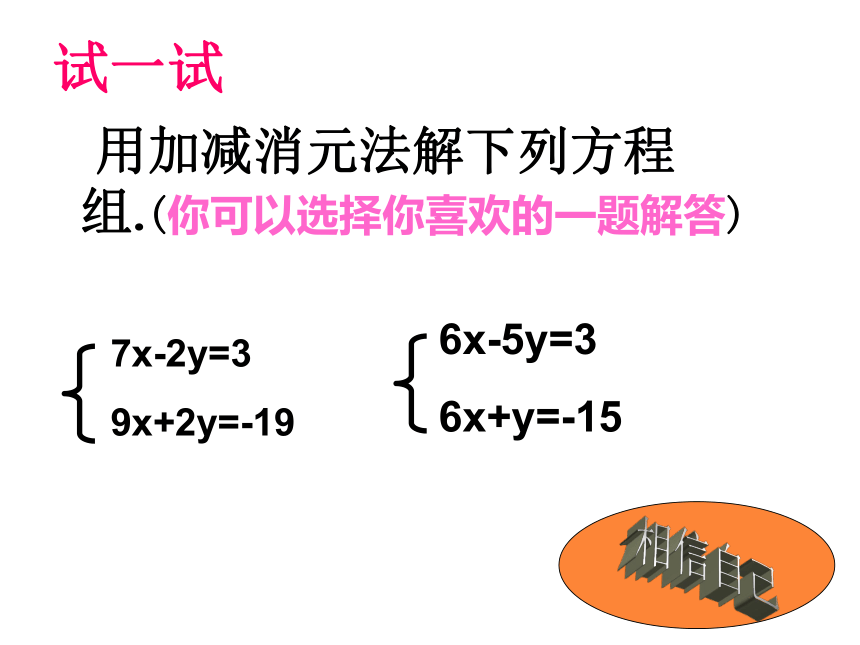
试一试
7x-2y=3
9x+2y=-19
6x-5y=3
6x+y=-15
用加减消元法解下列方程 组.(你可以选择你喜欢的一题解答)
1、选择题
1. 用加减法解方程组
6x+7y=-19①
6x-5y=17②
应用( )
A.①-②消去y
B. ①-②消去x
C. ②- ①消去常数项
D. 以上都不对
B
2.方程组
3x+2y=13
3x-2y=5
消去y后所得的方程是( )
B
A.6x=8
B.6x=18
C.6x=5
D.x=18
二、指出下列方程组求解过程中有错误步骤,并给予订正:
7x-4y=4
5x-4y=-4
解: ①-②,得
2x=4-4,
x=0
①
①
②
②
3x-4y=14
5x+4y=2
解:①-②,得
-2x=12
x =-6
解: ①-②,得
2x=4+4,
x=4
解: ①+②,得
8x=16
x =2
练一练
分别相加
y
1、已知方程组
x+3y=17
2x-3y=6
两个方程只要两边
就可以消去未知数
分别相减
2、已知方程组
25x-7y=16
25x+6y=10
两个方程只要两边
就可以消去未知数
x
已知a、b满足方程组
a+2b=8
2a+b=7
则a+b=
5
3、
(2)已知3a3xb2x-y和-7a8-yb7是同类项
求x·y
解:根据题意:得
3x=8-y
2x-y=7
转化为
3x+y=8
2x-y=7
x=3
y=-1
∴
即xy=-3
总结
总结评价
1、 易错点:在用加减法消元时,符号 易出现错误。
2、用加减法解二元一次方程组的条件:某一未知数系数的绝对值相等
基本思路:
主要步骤:
加减消元:
二元
一元
加减
消去一个元
求解
分别求出两个未知数的值
3、加减消元法解方程组基本思路是什么?
主要步骤有哪些?
变形
同一个未知数的系
数相同或互为相反数
4、. 二元一次方程组解法有 .
代入法、加减法
写解
写出方程组的解
当方程组中的一个未知数系数 的绝对值是1或一个方程的常数项为0时用代入消元法较方便。
当两个方程中同一个未知数的系数绝对值相等时,用加减消元法较方便。
知识拓展:
1、
3x2a+b+2
+5y3a-b+1=8
是关于x、y的二元一次方程
求a、b
解:根据题意:得
2a+b+2=1
3a-b+1=1
得:
a=
b=
1
5
-
3
5
-
已知(3m+2n-16)2与|3m-n-1|互为相反数
求:m+n的值
解:根据题意:得
3m+2n-16=0
3m-n-1=0
解得:
m=2
n=5
即:m+n=7
问题3:解方程组{
2(2x+1)=6-5y
3(y+1)=3-4x
解原方程组变形为{
4x+5y=4 ①
4x+3y=0 ②
①- ②得:2y=4
把y=2代入①得x=-1.5
{
X=-1.5
Y=2
y=2
问题4:已知方程组{
ax-by=4
ax+by=2
与方程组{
4x+3y=4
4x-5y=6
的解相同,求a,b
解:解方程组{
4x+3y=4
4x-5y=6
得
{
X=?
Y=?
将X=?Y=?代入{
ax-by=4
ax+by=2
由此可求出a=? b=?
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
反思小结 体验收获
知 识 的 升 华
独立
作业
1.当m为何值时,关于x、y的
方程组{ 得的解的和为12
2x+3y=m
3x+5y=m+2
y = 2 x – 1
3 x – 4 y = 2
(1)
(2)
x – y = 5
2 x + 4 y = 1
(3)
3 x = 5 y
2 x – 7 y = 3
(4)
3x + 5 y = 21
2x - 5 y = -11
用学过的方法解下列,想一想
还有其它的方法吗?方程组
和
互为相反数……
按照这种思路,你能消去
一个未知数吗?
?
(3x + 5y)+(2x - 5y)=21 + (-11)
分析:
3X+5y +2x - 5y=10
①左边 + ② 左边 = ① 右边 + ②右边
5x+0y =10
5x=10
解方程组
3x + 5y = 5
3x - 4y =23
①
②
解:
把 ① - ② 得
9y = -18
y = - 2
把 y = - 2 代入 ① , 得
3x + 5 × ( - 2 ) = 5
解得
x = 5
所以原方程组的解是
x = 5
y = - 2
当二元一次方程组中两个方程的某个未知数的系数互为相反数或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,进而求出二元一次方程组的解。
加减消元法
像这样,通过对方程组中的两个方程进行加或减的运算就可以消去一个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.
试一试
7x-2y=3
9x+2y=-19
6x-5y=3
6x+y=-15
用加减消元法解下列方程 组.(你可以选择你喜欢的一题解答)
1、选择题
1. 用加减法解方程组
6x+7y=-19①
6x-5y=17②
应用( )
A.①-②消去y
B. ①-②消去x
C. ②- ①消去常数项
D. 以上都不对
B
2.方程组
3x+2y=13
3x-2y=5
消去y后所得的方程是( )
B
A.6x=8
B.6x=18
C.6x=5
D.x=18
二、指出下列方程组求解过程中有错误步骤,并给予订正:
7x-4y=4
5x-4y=-4
解: ①-②,得
2x=4-4,
x=0
①
①
②
②
3x-4y=14
5x+4y=2
解:①-②,得
-2x=12
x =-6
解: ①-②,得
2x=4+4,
x=4
解: ①+②,得
8x=16
x =2
练一练
分别相加
y
1、已知方程组
x+3y=17
2x-3y=6
两个方程只要两边
就可以消去未知数
分别相减
2、已知方程组
25x-7y=16
25x+6y=10
两个方程只要两边
就可以消去未知数
x
已知a、b满足方程组
a+2b=8
2a+b=7
则a+b=
5
3、
(2)已知3a3xb2x-y和-7a8-yb7是同类项
求x·y
解:根据题意:得
3x=8-y
2x-y=7
转化为
3x+y=8
2x-y=7
x=3
y=-1
∴
即xy=-3
总结
总结评价
1、 易错点:在用加减法消元时,符号 易出现错误。
2、用加减法解二元一次方程组的条件:某一未知数系数的绝对值相等
基本思路:
主要步骤:
加减消元:
二元
一元
加减
消去一个元
求解
分别求出两个未知数的值
3、加减消元法解方程组基本思路是什么?
主要步骤有哪些?
变形
同一个未知数的系
数相同或互为相反数
4、. 二元一次方程组解法有 .
代入法、加减法
写解
写出方程组的解
当方程组中的一个未知数系数 的绝对值是1或一个方程的常数项为0时用代入消元法较方便。
当两个方程中同一个未知数的系数绝对值相等时,用加减消元法较方便。
知识拓展:
1、
3x2a+b+2
+5y3a-b+1=8
是关于x、y的二元一次方程
求a、b
解:根据题意:得
2a+b+2=1
3a-b+1=1
得:
a=
b=
1
5
-
3
5
-
已知(3m+2n-16)2与|3m-n-1|互为相反数
求:m+n的值
解:根据题意:得
3m+2n-16=0
3m-n-1=0
解得:
m=2
n=5
即:m+n=7
问题3:解方程组{
2(2x+1)=6-5y
3(y+1)=3-4x
解原方程组变形为{
4x+5y=4 ①
4x+3y=0 ②
①- ②得:2y=4
把y=2代入①得x=-1.5
{
X=-1.5
Y=2
y=2
问题4:已知方程组{
ax-by=4
ax+by=2
与方程组{
4x+3y=4
4x-5y=6
的解相同,求a,b
解:解方程组{
4x+3y=4
4x-5y=6
得
{
X=?
Y=?
将X=?Y=?代入{
ax-by=4
ax+by=2
由此可求出a=? b=?
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
反思小结 体验收获
知 识 的 升 华
独立
作业
1.当m为何值时,关于x、y的
方程组{ 得的解的和为12
2x+3y=m
3x+5y=m+2
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
