人教版数学九年级上册24.2.2.3直线与圆的位置关系切线长定理课件 (共21张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.2.2.3直线与圆的位置关系切线长定理课件 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 140.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 20:00:19 | ||
图片预览





文档简介
(共21张PPT)
24.2.2 直线和圆的位置关系
第3课时 切线长定理
1.掌握切线长定理,初步学会运用切线长定理进行计算
与证明.(重点)
2.学会利用方程思想解决几何问题,体验数形结合思想.
(难点)
学习目标
O.
P
A
B
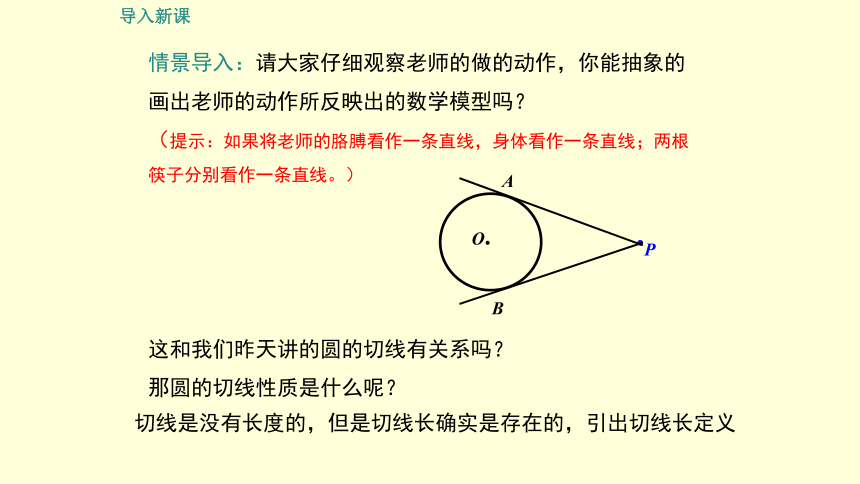
情景导入:请大家仔细观察老师的做的动作,你能抽象的画出老师的动作所反映出的数学模型吗?
(提示:如果将老师的胳膊看作一条直线,身体看作一条直线;两根筷子分别看作一条直线。)
导入新课
这和我们昨天讲的圆的切线有关系吗?
那圆的切线性质是什么呢?
切线是没有长度的,但是切线长确实是存在的,引出切线长定义
P
A
B
O
思考:切线长和切线的区别和联系?
切线长概念
切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长。
小结:切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。
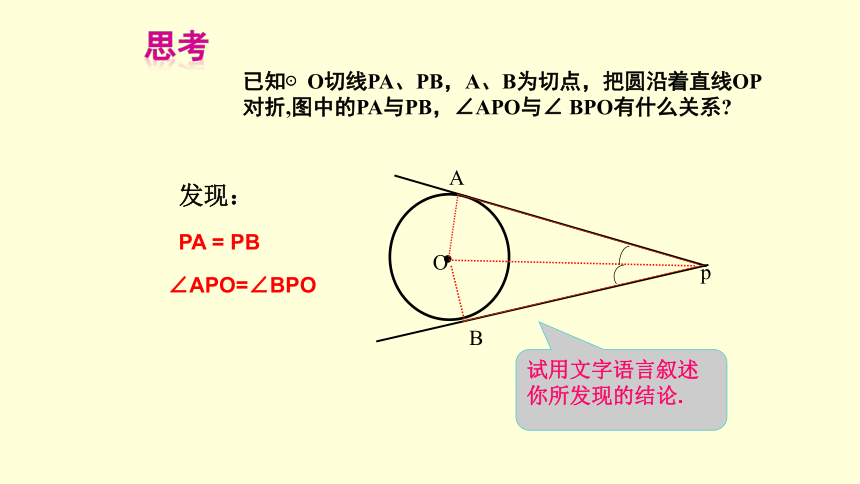
思考
PA = PB
∠APO=∠BPO
发现:
p
A
B
O
试用文字语言叙述你所发现的结论.
已知⊙O切线PA、PB,A、B为切点,把圆沿着直线OP对折,图中的PA与PB,∠APO与∠ BPO有什么关系
思考:PA、PB分别是⊙O的两条切线,A、B为切点,且AP⊥OA,BP⊥OB,那你能找出图中相等的线段和相等的角吗?
O.
P
A
B
探究切线长定理
PA、PB分别切⊙O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
切线长定理为证明线段相等、角相等提供新的方法
切线长定理
p
A
B
O
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
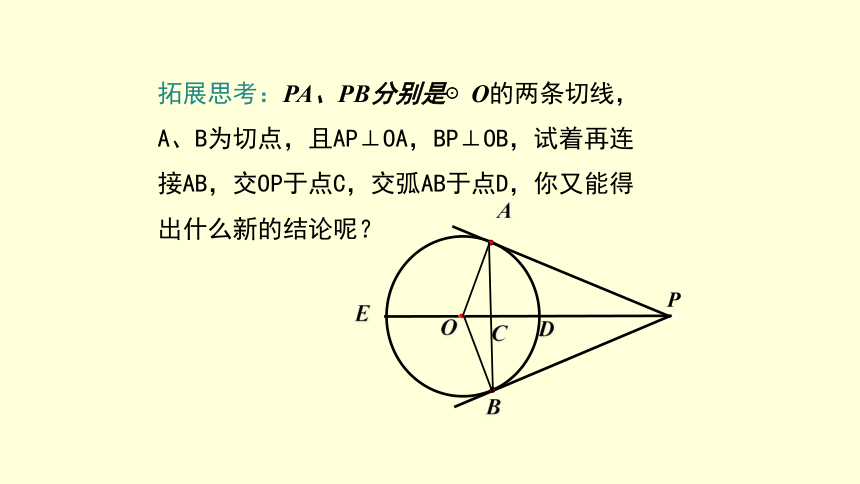
拓展思考:PA、PB分别是⊙O的两条切线,A、B为切点,且AP⊥OA,BP⊥OB,试着再连接AB,交OP于点C,交弧AB于点D,你又能得出什么新的结论呢?
B
P
O
A
C
E
D
B
P
O
A
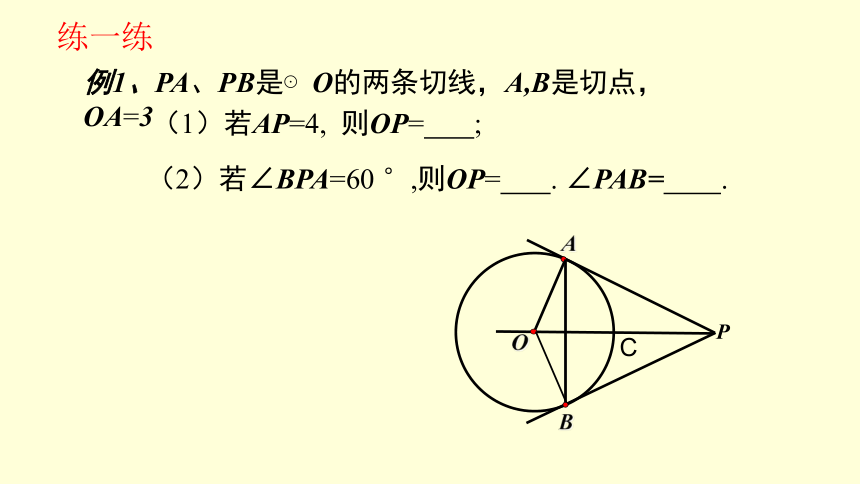
例1、PA、PB是⊙O的两条切线,A,B是切点,OA=3
(1)若AP=4, 则OP= ;
(2)若∠BPA=60 °,则OP= . ∠PAB= .
C
练一练
练2、如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若AP= 12,∠P=60o,求弦AB的长.
变式:如图,AC为⊙O的直径,PA、PB是⊙O的两条切线,切点分别为点A、B,若AC= 12,∠P=60o,求弦AB的长.
要点归纳
切线长问题辅助线添加方法
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和
角相等的新方法
辅助线
课堂小结
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
一判断
(1)过任意一点总可以作圆的两条切线( )
(2)从圆外一点引圆的两条切线,它们的长相等。( )
(1)如图PA、PB切圆于A、B两点, 连结PO,则 度。
25
P
B
O
A
二填空选择
随堂演练
(2)如图,Δ ABC的边BC,AC,AB分别切圆于D,E,F;如果AF=2cm,BD=7cm,CE=4cm,则BC= cm, AC=
AB=
B
D
A
C
F
E
2
7
4
( 2 )等腰三角形有 个,分别是
三、综合练习
已知:如图PA、PB是⊙ O的两条切线,A、B为切点。直线OP交⊙ O于D、E,交AB于C。
O
P
A
B
C
D
E
(1)图中互相垂直的关系有 对,分别是
(3)图中全等三角形 对,分别是
思考
三角形的内切圆
拓展知识
1.与三角形三边都相切 圆是否存在?
2.假如存在,圆心在哪儿?如何找到?
三角形内切圆
o
A
B
C
1. 与三角形各边都相切的圆叫做三角形的内切圆。
2. 三角形三个内角平分线的交点,叫做三角形的内心。
3. 交点到三角形任意一边的垂直距离,是内切圆的半径。
如图, △ABC的内切圆⊙O与BC 、CA、 AB 分别相交于点D 、 E 、 F ,且AB=9,BC =14, CA =13,求AF、BD、CE的长。
A
E
C
D
B
F
例1:
O
拓展延伸
例2:已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为弧AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12
(1)求△PEF的周长
(2)若∠P=50°,∠EOF的度数.
E
A
Q
P
F
B
O
例3:在△ABC中,AB=5cm, BC=7cm,AC=8cm, ⊙O与BC、AC、 AB分别相切于 D、 E 、F,求 AE、 BD 、CF的长?
24.2.2 直线和圆的位置关系
第3课时 切线长定理
1.掌握切线长定理,初步学会运用切线长定理进行计算
与证明.(重点)
2.学会利用方程思想解决几何问题,体验数形结合思想.
(难点)
学习目标
O.
P
A
B
情景导入:请大家仔细观察老师的做的动作,你能抽象的画出老师的动作所反映出的数学模型吗?
(提示:如果将老师的胳膊看作一条直线,身体看作一条直线;两根筷子分别看作一条直线。)
导入新课
这和我们昨天讲的圆的切线有关系吗?
那圆的切线性质是什么呢?
切线是没有长度的,但是切线长确实是存在的,引出切线长定义
P
A
B
O
思考:切线长和切线的区别和联系?
切线长概念
切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长。
小结:切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。
思考
PA = PB
∠APO=∠BPO
发现:
p
A
B
O
试用文字语言叙述你所发现的结论.
已知⊙O切线PA、PB,A、B为切点,把圆沿着直线OP对折,图中的PA与PB,∠APO与∠ BPO有什么关系
思考:PA、PB分别是⊙O的两条切线,A、B为切点,且AP⊥OA,BP⊥OB,那你能找出图中相等的线段和相等的角吗?
O.
P
A
B
探究切线长定理
PA、PB分别切⊙O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
切线长定理为证明线段相等、角相等提供新的方法
切线长定理
p
A
B
O
从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
拓展思考:PA、PB分别是⊙O的两条切线,A、B为切点,且AP⊥OA,BP⊥OB,试着再连接AB,交OP于点C,交弧AB于点D,你又能得出什么新的结论呢?
B
P
O
A
C
E
D
B
P
O
A
例1、PA、PB是⊙O的两条切线,A,B是切点,OA=3
(1)若AP=4, 则OP= ;
(2)若∠BPA=60 °,则OP= . ∠PAB= .
C
练一练
练2、如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若AP= 12,∠P=60o,求弦AB的长.
变式:如图,AC为⊙O的直径,PA、PB是⊙O的两条切线,切点分别为点A、B,若AC= 12,∠P=60o,求弦AB的长.
要点归纳
切线长问题辅助线添加方法
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和
角相等的新方法
辅助线
课堂小结
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
一判断
(1)过任意一点总可以作圆的两条切线( )
(2)从圆外一点引圆的两条切线,它们的长相等。( )
(1)如图PA、PB切圆于A、B两点, 连结PO,则 度。
25
P
B
O
A
二填空选择
随堂演练
(2)如图,Δ ABC的边BC,AC,AB分别切圆于D,E,F;如果AF=2cm,BD=7cm,CE=4cm,则BC= cm, AC=
AB=
B
D
A
C
F
E
2
7
4
( 2 )等腰三角形有 个,分别是
三、综合练习
已知:如图PA、PB是⊙ O的两条切线,A、B为切点。直线OP交⊙ O于D、E,交AB于C。
O
P
A
B
C
D
E
(1)图中互相垂直的关系有 对,分别是
(3)图中全等三角形 对,分别是
思考
三角形的内切圆
拓展知识
1.与三角形三边都相切 圆是否存在?
2.假如存在,圆心在哪儿?如何找到?
三角形内切圆
o
A
B
C
1. 与三角形各边都相切的圆叫做三角形的内切圆。
2. 三角形三个内角平分线的交点,叫做三角形的内心。
3. 交点到三角形任意一边的垂直距离,是内切圆的半径。
如图, △ABC的内切圆⊙O与BC 、CA、 AB 分别相交于点D 、 E 、 F ,且AB=9,BC =14, CA =13,求AF、BD、CE的长。
A
E
C
D
B
F
例1:
O
拓展延伸
例2:已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为弧AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12
(1)求△PEF的周长
(2)若∠P=50°,∠EOF的度数.
E
A
Q
P
F
B
O
例3:在△ABC中,AB=5cm, BC=7cm,AC=8cm, ⊙O与BC、AC、 AB分别相切于 D、 E 、F,求 AE、 BD 、CF的长?
同课章节目录
