2021-2022学年冀教版八年级数学上册第17章+特殊三角形+单元练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学上册第17章+特殊三角形+单元练习题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 299.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 20:50:53 | ||
图片预览


文档简介
2021-2022学年冀教版八年级数学上册《第17章特殊三角形》单元综合练习题(附答案)
1.如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是( )
A.SSS B.SAS C.ASA D.HL
2.下列不能使两个直角三角形全等的条件是( )
A.三边对应相等 B.两个锐角相等
C.一条直角边和斜边对应相等 D.两条直角边对应相等
3.如图,已知在△ABC中,AB=AC=5,BC=3,MN垂直平分AB,且与AC相交于点D,则△BDC的周长为( )
A.8 B.10 C.11 D.13
4.已知等腰三角形的周长为21,其中一边长为5,则该等腰三角形的底边长是( )
A.5 B.8 C.11 D.5或11
5.如图,在3×3的正方形网格中,A,B是两个格点,连接AB,在网格中找到一个格点C,使得△ABC是以AB为腰的等腰三角形,满足条件的格点C的个数是( )
A.5 B.6 C.7 D.8
6.如右图所示:在△ABC中,AB=AC,∠A=36°,BD是∠ABC的平分线,那么图中等腰三角形有( )
A.1个 B.2个 C.3个 D.4个
7.已知a,b,c分别是等腰△ABC三边的长,且满足ac=12﹣bc,若a,b,c均为正整数,则这样的等腰△ABC存在( )
A.3个 B.4个 C.5个 D.6个
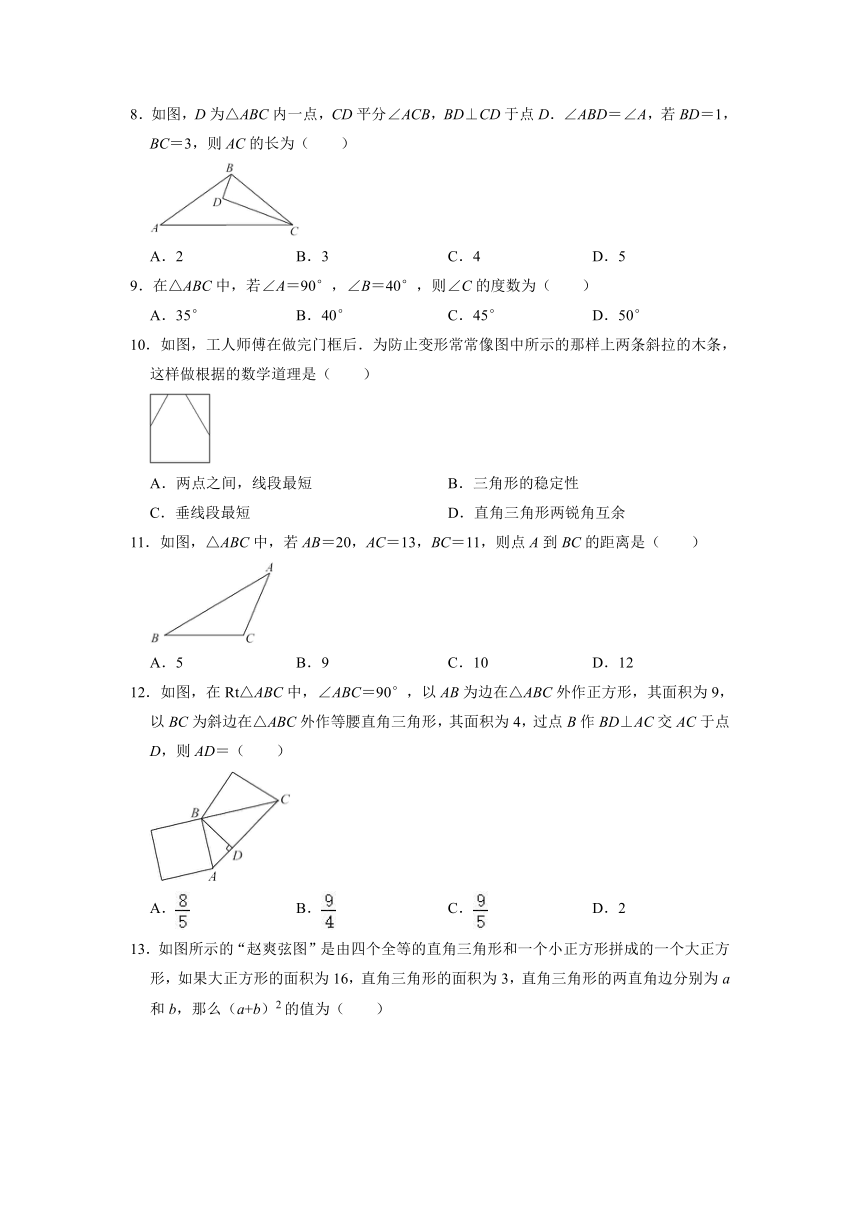
8.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD于点D.∠ABD=∠A,若BD=1,BC=3,则AC的长为( )
A.2 B.3 C.4 D.5
9.在△ABC中,若∠A=90°,∠B=40°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
10.如图,工人师傅在做完门框后.为防止变形常常像图中所示的那样上两条斜拉的木条,这样做根据的数学道理是( )
A.两点之间,线段最短 B.三角形的稳定性
C.垂线段最短 D.直角三角形两锐角互余
11.如图,△ABC中,若AB=20,AC=13,BC=11,则点A到BC的距离是( )
A.5 B.9 C.10 D.12
12.如图,在Rt△ABC中,∠ABC=90°,以AB为边在△ABC外作正方形,其面积为9,以BC为斜边在△ABC外作等腰直角三角形,其面积为4,过点B作BD⊥AC交AC于点D,则AD=( )
A. B. C. D.2
13.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,如果大正方形的面积为16,直角三角形的面积为3,直角三角形的两直角边分别为a和b,那么(a+b)2的值为( )
A.18 B.22 C.28 D.36
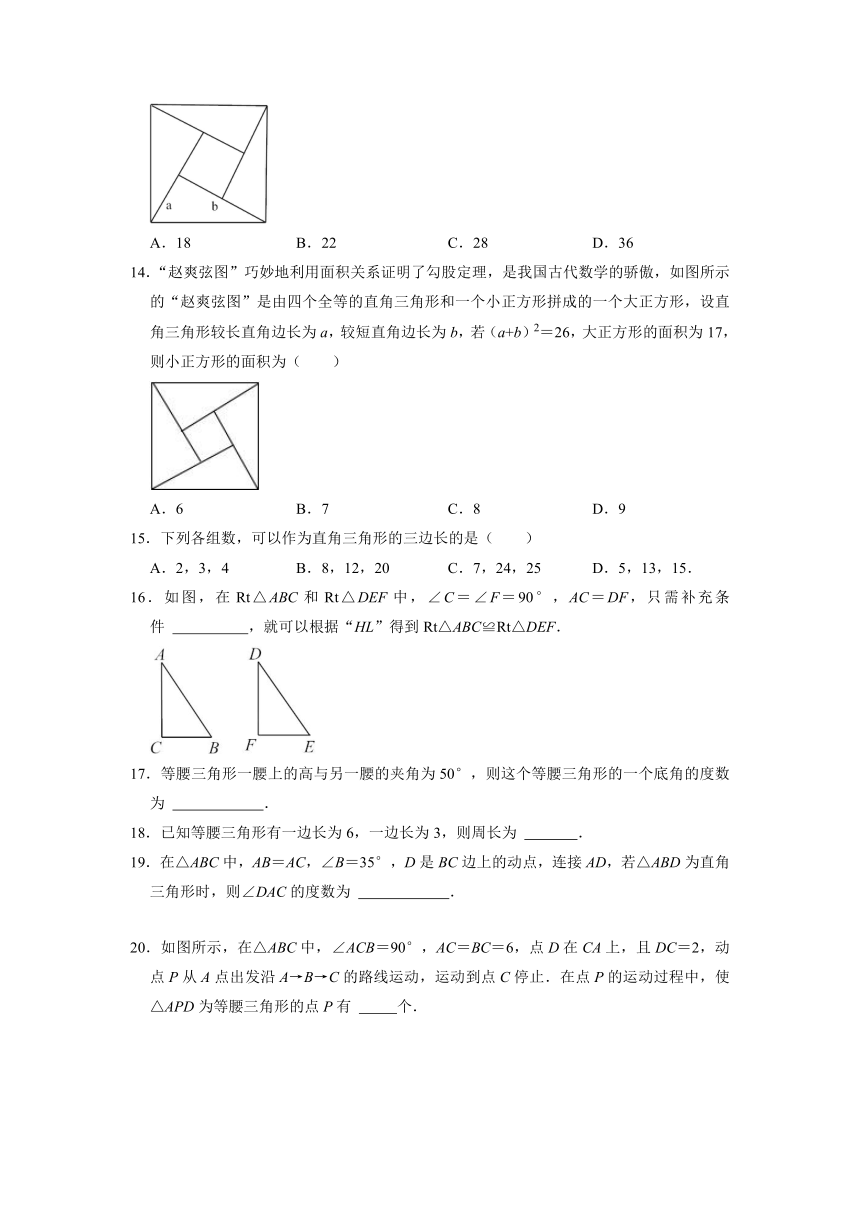
14.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=26,大正方形的面积为17,则小正方形的面积为( )
A.6 B.7 C.8 D.9
15.下列各组数,可以作为直角三角形的三边长的是( )
A.2,3,4 B.8,12,20 C.7,24,25 D.5,13,15.
16.如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=DF,只需补充条件 ,就可以根据“HL”得到Rt△ABC≌Rt△DEF.
17.等腰三角形一腰上的高与另一腰的夹角为50°,则这个等腰三角形的一个底角的度数为 .
18.已知等腰三角形有一边长为6,一边长为3,则周长为 .
19.在△ABC中,AB=AC,∠B=35°,D是BC边上的动点,连接AD,若△ABD为直角三角形时,则∠DAC的度数为 .
20.如图所示,在△ABC中,∠ACB=90°,AC=BC=6,点D在CA上,且DC=2,动点P从A点出发沿A→B→C的路线运动,运动到点C停止.在点P的运动过程中,使△APD为等腰三角形的点P有 个.
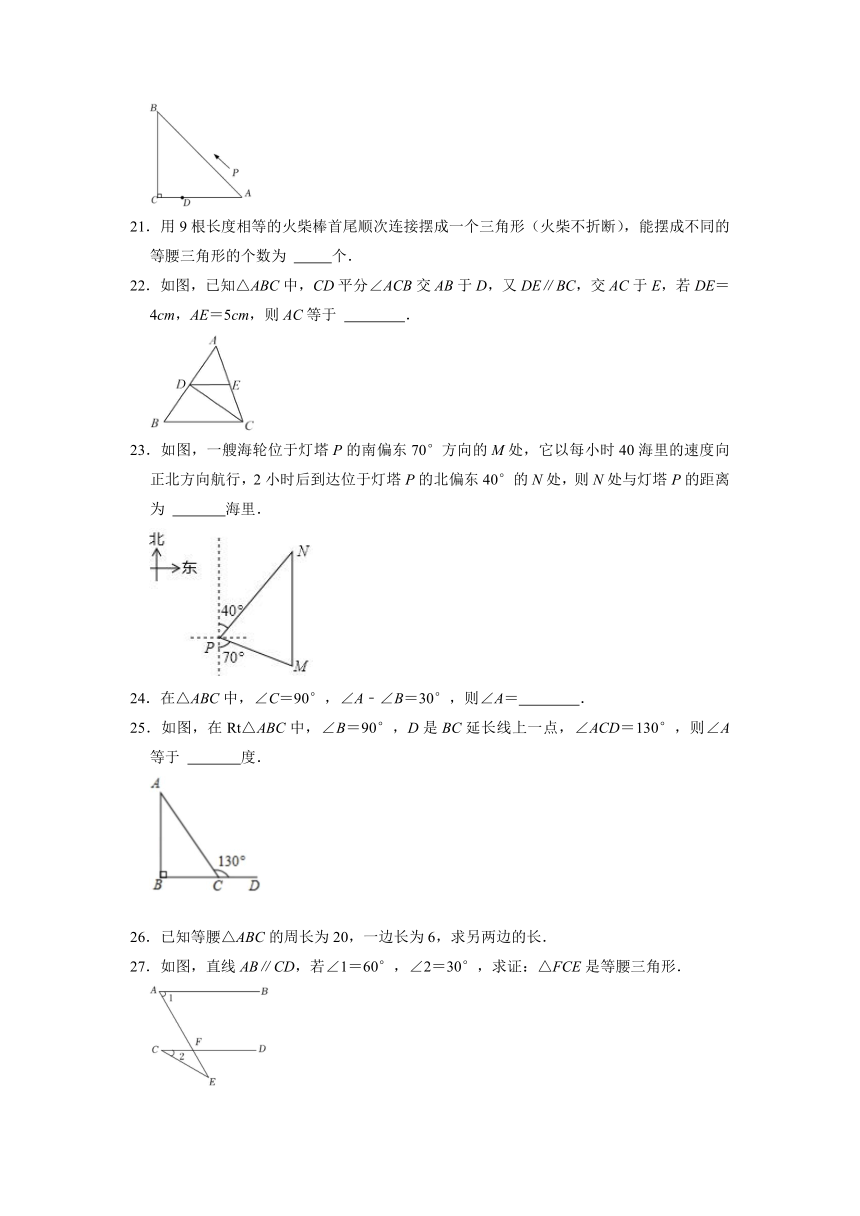
21.用9根长度相等的火柴棒首尾顺次连接摆成一个三角形(火柴不折断),能摆成不同的等腰三角形的个数为 个.
22.如图,已知△ABC中,CD平分∠ACB交AB于D,又DE∥BC,交AC于E,若DE=4cm,AE=5cm,则AC等于 .
23.如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为 海里.
24.在△ABC中,∠C=90°,∠A﹣∠B=30°,则∠A= .
25.如图,在Rt△ABC中,∠B=90°,D是BC延长线上一点,∠ACD=130°,则∠A等于 度.
26.已知等腰△ABC的周长为20,一边长为6,求另两边的长.
27.如图,直线AB∥CD,若∠1=60°,∠2=30°,求证:△FCE是等腰三角形.
28.如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,PQ经过点O,与AB、AC分别相交于点P、Q.
(1)若∠A=70°,求∠BOC的度数;
(2)若△ABC的周长为32,BC=13,且PQ∥BC,求△APQ的周长.
29.在Rt△ABC中,两个锐角的平分线AO,BO相交于点O,求∠AOB的度数.
30.如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若动点P从点A出发,以每秒1cm的速度沿折线A﹣C﹣B运动,设运动时间为t秒(t>0).
(1)当点P在AB边的垂直平分线上时,求t的值;
(2)当点P在∠BAC的平分线上时,求t的值.
参考答案
1.解:由图得:遮挡住的三角形中露出两个角及其夹边.
∴根据三角形的判定方法ASA可解决此题.
故选:C.
2.解:A、三边对应相等,利用SSS能证明两三角形全等,故本选项不符合题意;
B、两个锐角对应相等时,加上已知的直角相等,由AAA不能判定它们全等,故本选项符合题意;
C、一条直角边和斜边对应相等,利用HL能证明两三角形全等,故本选项不符合题意;
D、两条直角边对应相等,加上已知的直角相等,利用SAS能证明两三角形全等,故本选项不符合题意;
故选:B.
3.解:∵MN垂直平分AB,
∴AD=BD,
∴△BDC的周长=BD+BC+CD=AD+DC+BC=AC+BC=5+3=8,
故选:A.
4.解:当腰长为5时,底边长为21﹣2×5=11,三角形的三边长为5,5,11,不能构成三角形;
当底边长为5时,腰长为(21﹣5)÷2=8,三角形的三边长为8,8,5,构成等腰三角形;
所以等腰三角形的底边为5.
故选:A.
5.解:如图,以AB为等腰△ABC其中的一条腰时,符合条件的C点有5个.
故选:A.
6.解:∵BD是△ABC的角平分线,
∴∠ABC=2∠ABD=72°,
∴∠ABC=∠C=72°,
∴△ABC是等腰三角形…①.
∠A=180°﹣2∠ABC=180°﹣2×72°=36°,
∴∠A=∠ABD,
∴△ABD是等腰三角形…②.
∵∠DBC=∠ABD=36°,∠C=72°,
∴∠BDC=72°,
∴∠BDC=∠C,
∴△BDC是等腰三角形…③.
故图中的等腰三角形有3个.
故选:C.
7.解:∵ac=12﹣bc,
∴ac+bc=12,
∴(a+b)c=12,
∴12=1×12=2×6=3×4,a+b>c,
∴ 或或,
当 时,三边长分别为 1,6,6或 1,1,11 (不合题意舍去);
当 时,三边长分别为 2,3,3或 2,2,4 (不合题意舍去);
当 时,三边长分别为 3,2,2或 3,3,1,
所以一共有4个,
故选:B.
8.解:延长BD交AC于E,如图,
∵CD平分∠ACB,BD⊥CD,
∴△BCE为等腰三角形,
∴DE=BD=1,CE=CB=3,
∵∠A=∠ABD,
∴EA=EB=2,
∴AC=AE+CE=2+3=5.
故选:D.
9.解:∵∠A=90°,
∴∠B+∠C=90°,
∵∠B=40°,
∴∠C=90°﹣40°=50°,
故选:D.
10.解:这样做根据的数学道理是三角形的稳定性,
故选:B.
11.解:过A作AD⊥BC交BC的延长线于D,
∴∠D=90°,
∴AB2﹣BD2=AD2=AC2﹣CD2,
∵AB=20,AC=13,BC=11,
∴202﹣(11+CD)2=132﹣CD2,
∴CD=5,
∴AD===12,
∴点A到BC的距离是12,
故选:D.
12.解:∵以AB为边的正方形的面积为9,
∴AB2=9,
∵以BC为斜边的等腰直角三角形的面积为4,
∴等腰直角三角形的腰长为2,
∴BC2=16,
在Rt△ABC中,∠ABC=90°,
则AC===5,
∵S△ABC=×AB×AC=×AC×BD,
∴×3×4=×5×BD,
解得:BD=,
由勾股定理得:AD===,
故选:C.
13.解:大正方形的面积为16,得到它的边长为4,
即得a2+b2=42=16,ab=3,
由题意4×3+(a﹣b)2=16,ab=6,
所以(a﹣b)2=4,
所以(a+b)2=(a﹣b)2+4ab=4+4×6=28,
故选:C.
14.解:如图所示:
∵(a+b)2=26,
∴a2+2ab+b2=26,
∵大正方形的面积为17,
∴2ab=26﹣17=9,
∴小正方形的面积为17﹣9=8,
故选:C.
15.解:A、22+32≠42,∴三角形不是直角三角形,故选项不符合题意;
B、82+122≠202,∴此三角形不是直角三角形,故选项不符合题意;
C、72+242=252,∴三角形是直角三角形,故选项符合题意;
D、52+132≠152,∴三角形不是直角三角形,故选项不符合题意.
故选:C.
16.解:补充条件:AB=DE.
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL).
故答案为:AB=DE.
17.解:当这个三角形是锐角三角形时:高与另一腰的夹角为50,则顶角是40°,因而底角是70°;
如图所示:当这个三角形是钝角三角形时:∠ABD=40°,BD⊥CD,
故∠BAD=40°,
所以∠B=∠C=20°,
因此这个等腰三角形的一个底角的度数为20°或70°.
故答案为:20°或70°.
18.解:∵如果腰长为3,则3+3=6,不符合三角形三边关系,
所以腰长只能为6.
∴其周长6+6+3=15.
故答案为:15.
19.解:如图,∵AB=AC,∠B=35°,
∴∠B=∠C=35°,
∴∠BAC=110°,
当∠BAD=90°时,
∠DAC=110°﹣90°=20°;
当∠ADB=90°时,
∵AB=AC,AD⊥BC,
∴∠DAC=∠BAD=55°.
故答案为:20°或55°.
20.解:如图,
根据已知,∠ACB=90°,AC=BC=6,点D在CA上,且DC=2,
∴AD=AC﹣CD=4,∠BAC=45°,
①作DP1⊥AB于P1,则三角形AP1D是等腰三角形;
②当AP2=AD=4时,三角形AP2D是等腰三角形;
③作DP3⊥AC,垂足为D,交AB于P3,则三角形AP3D是等腰三角形;
④当点P在BC上,AD=PD=4时,三角形AP4D是等腰三角形.
故使△APD为等腰三角形的点P有4个.
故答案为:4.
21.解:根据三角形三边关系,能摆成两种不同的等腰三角形,分别为:
①腰和底边都由3根火柴棒组成;②腰由4根火柴棒组成,底边有1根火柴棒,
故答案为:2.
22.解:∵CD平分∠ACB交AB于D,
∴∠ACD=∠DCB,
∵DE∥BC,
∴∠EDC=∠DCB,
∴∠EDC=∠ECD,
∴DE=EC=4cm,
∵AE=5cm,
∴AC=AE+EC=5+4=9(cm).
故答案为:9cm.
23.解:∵∠NPM=180°﹣70°﹣40°=70°,
∵向北的方向线是平行的,
∴∠M=70°,
∴∠NPM=∠M,
∴NP=MN=40×2=80(海里),
故答案为:80.
24.解:在△ABC中,∠C=90°,
则∠A+∠B=90°,
由题意得,
解得:∠A=60°,∠B=30°,
故答案为:60°.
25.解:∵∠B=90°,∠ACD=130°,∠A+∠B=∠ACD,
∴∠A=∠ACD﹣∠B=130°﹣90°=40°,
故答案为:40.
26.解:当腰为6时,则另两边长为6、20﹣6×2=8,此时三边满足三角形三边关系,即此时三角形的另两边为6,8;
当底边为6时,则另两边长为(20﹣6)=7,此时三边满足三角形三边关系,即此时三角形的另两边为7,7;
综上可知三角形的另两边长为6,8或7,7.
27.证明:∵AB∥CD,
∴∠DFE=∠1=60°,
∴∠CFE=180°﹣∠DFE,
=180°﹣60°,
=120°,
∴∠CEF=180°﹣∠2﹣∠CFE
=180°﹣30°﹣120°
=30°,
∴∠2=∠CEF,
∴CF=EF,
∴△FCE是等腰三角形.
28.解:(1)∵BO平分∠ABC,CO平分∠ACB,
∴∠PBO=∠CBO,∠QCO=∠BCO,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣∠A)==55°,
∴∠BOC=180°﹣55°=125°;
(2)∵PQ∥BC,
∴∠POB=∠PBO,
∴PB=PO,
同理可得QO=QC,
∴△APQ的周长为AP+PO+AQ+QO=AB+AC,
又∵△ABC的周长为32,BC=13,
∴AB+AC=32﹣13=19,
∴△APQ的周长为19.
29.解:∵∠C=90°,
∴∠CAB+∠CBA=90°,
∵BO、AO分别平分∠CBA、∠CAB,
∴∠2=∠CBA,∠1=∠CAB,
∴∠1+∠2=∠CBA+∠CAB=(∠CBA+∠CAB)=×90°=45°,
∴∠AOB=180°﹣(∠1+∠2)=180°﹣45°=135°.
30.解:(1)如图1,当点P在边AB的垂直平分线上时,
过点P作PD⊥AB于点D,连接BP,则PA=PB=t(cm),
∵∠ACB=90°,AB=10cm,BC=6cm,
∴AC=8cm,
∴PC=(8﹣t)cm,
在Rt△PCB中,由勾股定理得:PC2+BC2=PB2,即(8﹣t)2+62=t2,
解得:,
∴点P在AB边的垂直平分线上时,求t的值为.
(2)当点P在BC上时,
如图2,过点P作PE⊥AB,
∵AP平分∠BAC且PC⊥AC,
∴PC=PE=(t﹣8)cm,
∴PB=(14﹣t)cm,
在△ACP与△AEP中,
,
∴△ACP≌△AEP(AAS),
∴AE=AC=8cm,
∴BE=AB﹣AE=10﹣8=2cm,
在Rt△PEB中,由勾股定理得:PE2+EB2=PB2,
∴(t﹣8)2+22=(14﹣t)2,
解得:,
∴当点P在∠BAC的平分线上时,t的值为.
1.如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是( )
A.SSS B.SAS C.ASA D.HL
2.下列不能使两个直角三角形全等的条件是( )
A.三边对应相等 B.两个锐角相等
C.一条直角边和斜边对应相等 D.两条直角边对应相等
3.如图,已知在△ABC中,AB=AC=5,BC=3,MN垂直平分AB,且与AC相交于点D,则△BDC的周长为( )
A.8 B.10 C.11 D.13
4.已知等腰三角形的周长为21,其中一边长为5,则该等腰三角形的底边长是( )
A.5 B.8 C.11 D.5或11
5.如图,在3×3的正方形网格中,A,B是两个格点,连接AB,在网格中找到一个格点C,使得△ABC是以AB为腰的等腰三角形,满足条件的格点C的个数是( )
A.5 B.6 C.7 D.8
6.如右图所示:在△ABC中,AB=AC,∠A=36°,BD是∠ABC的平分线,那么图中等腰三角形有( )
A.1个 B.2个 C.3个 D.4个
7.已知a,b,c分别是等腰△ABC三边的长,且满足ac=12﹣bc,若a,b,c均为正整数,则这样的等腰△ABC存在( )
A.3个 B.4个 C.5个 D.6个
8.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD于点D.∠ABD=∠A,若BD=1,BC=3,则AC的长为( )
A.2 B.3 C.4 D.5
9.在△ABC中,若∠A=90°,∠B=40°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
10.如图,工人师傅在做完门框后.为防止变形常常像图中所示的那样上两条斜拉的木条,这样做根据的数学道理是( )
A.两点之间,线段最短 B.三角形的稳定性
C.垂线段最短 D.直角三角形两锐角互余
11.如图,△ABC中,若AB=20,AC=13,BC=11,则点A到BC的距离是( )
A.5 B.9 C.10 D.12
12.如图,在Rt△ABC中,∠ABC=90°,以AB为边在△ABC外作正方形,其面积为9,以BC为斜边在△ABC外作等腰直角三角形,其面积为4,过点B作BD⊥AC交AC于点D,则AD=( )
A. B. C. D.2
13.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,如果大正方形的面积为16,直角三角形的面积为3,直角三角形的两直角边分别为a和b,那么(a+b)2的值为( )
A.18 B.22 C.28 D.36
14.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=26,大正方形的面积为17,则小正方形的面积为( )
A.6 B.7 C.8 D.9
15.下列各组数,可以作为直角三角形的三边长的是( )
A.2,3,4 B.8,12,20 C.7,24,25 D.5,13,15.
16.如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=DF,只需补充条件 ,就可以根据“HL”得到Rt△ABC≌Rt△DEF.
17.等腰三角形一腰上的高与另一腰的夹角为50°,则这个等腰三角形的一个底角的度数为 .
18.已知等腰三角形有一边长为6,一边长为3,则周长为 .
19.在△ABC中,AB=AC,∠B=35°,D是BC边上的动点,连接AD,若△ABD为直角三角形时,则∠DAC的度数为 .
20.如图所示,在△ABC中,∠ACB=90°,AC=BC=6,点D在CA上,且DC=2,动点P从A点出发沿A→B→C的路线运动,运动到点C停止.在点P的运动过程中,使△APD为等腰三角形的点P有 个.
21.用9根长度相等的火柴棒首尾顺次连接摆成一个三角形(火柴不折断),能摆成不同的等腰三角形的个数为 个.
22.如图,已知△ABC中,CD平分∠ACB交AB于D,又DE∥BC,交AC于E,若DE=4cm,AE=5cm,则AC等于 .
23.如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为 海里.
24.在△ABC中,∠C=90°,∠A﹣∠B=30°,则∠A= .
25.如图,在Rt△ABC中,∠B=90°,D是BC延长线上一点,∠ACD=130°,则∠A等于 度.
26.已知等腰△ABC的周长为20,一边长为6,求另两边的长.
27.如图,直线AB∥CD,若∠1=60°,∠2=30°,求证:△FCE是等腰三角形.
28.如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,PQ经过点O,与AB、AC分别相交于点P、Q.
(1)若∠A=70°,求∠BOC的度数;
(2)若△ABC的周长为32,BC=13,且PQ∥BC,求△APQ的周长.
29.在Rt△ABC中,两个锐角的平分线AO,BO相交于点O,求∠AOB的度数.
30.如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若动点P从点A出发,以每秒1cm的速度沿折线A﹣C﹣B运动,设运动时间为t秒(t>0).
(1)当点P在AB边的垂直平分线上时,求t的值;
(2)当点P在∠BAC的平分线上时,求t的值.
参考答案
1.解:由图得:遮挡住的三角形中露出两个角及其夹边.
∴根据三角形的判定方法ASA可解决此题.
故选:C.
2.解:A、三边对应相等,利用SSS能证明两三角形全等,故本选项不符合题意;
B、两个锐角对应相等时,加上已知的直角相等,由AAA不能判定它们全等,故本选项符合题意;
C、一条直角边和斜边对应相等,利用HL能证明两三角形全等,故本选项不符合题意;
D、两条直角边对应相等,加上已知的直角相等,利用SAS能证明两三角形全等,故本选项不符合题意;
故选:B.
3.解:∵MN垂直平分AB,
∴AD=BD,
∴△BDC的周长=BD+BC+CD=AD+DC+BC=AC+BC=5+3=8,
故选:A.
4.解:当腰长为5时,底边长为21﹣2×5=11,三角形的三边长为5,5,11,不能构成三角形;
当底边长为5时,腰长为(21﹣5)÷2=8,三角形的三边长为8,8,5,构成等腰三角形;
所以等腰三角形的底边为5.
故选:A.
5.解:如图,以AB为等腰△ABC其中的一条腰时,符合条件的C点有5个.
故选:A.
6.解:∵BD是△ABC的角平分线,
∴∠ABC=2∠ABD=72°,
∴∠ABC=∠C=72°,
∴△ABC是等腰三角形…①.
∠A=180°﹣2∠ABC=180°﹣2×72°=36°,
∴∠A=∠ABD,
∴△ABD是等腰三角形…②.
∵∠DBC=∠ABD=36°,∠C=72°,
∴∠BDC=72°,
∴∠BDC=∠C,
∴△BDC是等腰三角形…③.
故图中的等腰三角形有3个.
故选:C.
7.解:∵ac=12﹣bc,
∴ac+bc=12,
∴(a+b)c=12,
∴12=1×12=2×6=3×4,a+b>c,
∴ 或或,
当 时,三边长分别为 1,6,6或 1,1,11 (不合题意舍去);
当 时,三边长分别为 2,3,3或 2,2,4 (不合题意舍去);
当 时,三边长分别为 3,2,2或 3,3,1,
所以一共有4个,
故选:B.
8.解:延长BD交AC于E,如图,
∵CD平分∠ACB,BD⊥CD,
∴△BCE为等腰三角形,
∴DE=BD=1,CE=CB=3,
∵∠A=∠ABD,
∴EA=EB=2,
∴AC=AE+CE=2+3=5.
故选:D.
9.解:∵∠A=90°,
∴∠B+∠C=90°,
∵∠B=40°,
∴∠C=90°﹣40°=50°,
故选:D.
10.解:这样做根据的数学道理是三角形的稳定性,
故选:B.
11.解:过A作AD⊥BC交BC的延长线于D,
∴∠D=90°,
∴AB2﹣BD2=AD2=AC2﹣CD2,
∵AB=20,AC=13,BC=11,
∴202﹣(11+CD)2=132﹣CD2,
∴CD=5,
∴AD===12,
∴点A到BC的距离是12,
故选:D.
12.解:∵以AB为边的正方形的面积为9,
∴AB2=9,
∵以BC为斜边的等腰直角三角形的面积为4,
∴等腰直角三角形的腰长为2,
∴BC2=16,
在Rt△ABC中,∠ABC=90°,
则AC===5,
∵S△ABC=×AB×AC=×AC×BD,
∴×3×4=×5×BD,
解得:BD=,
由勾股定理得:AD===,
故选:C.
13.解:大正方形的面积为16,得到它的边长为4,
即得a2+b2=42=16,ab=3,
由题意4×3+(a﹣b)2=16,ab=6,
所以(a﹣b)2=4,
所以(a+b)2=(a﹣b)2+4ab=4+4×6=28,
故选:C.
14.解:如图所示:
∵(a+b)2=26,
∴a2+2ab+b2=26,
∵大正方形的面积为17,
∴2ab=26﹣17=9,
∴小正方形的面积为17﹣9=8,
故选:C.
15.解:A、22+32≠42,∴三角形不是直角三角形,故选项不符合题意;
B、82+122≠202,∴此三角形不是直角三角形,故选项不符合题意;
C、72+242=252,∴三角形是直角三角形,故选项符合题意;
D、52+132≠152,∴三角形不是直角三角形,故选项不符合题意.
故选:C.
16.解:补充条件:AB=DE.
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL).
故答案为:AB=DE.
17.解:当这个三角形是锐角三角形时:高与另一腰的夹角为50,则顶角是40°,因而底角是70°;
如图所示:当这个三角形是钝角三角形时:∠ABD=40°,BD⊥CD,
故∠BAD=40°,
所以∠B=∠C=20°,
因此这个等腰三角形的一个底角的度数为20°或70°.
故答案为:20°或70°.
18.解:∵如果腰长为3,则3+3=6,不符合三角形三边关系,
所以腰长只能为6.
∴其周长6+6+3=15.
故答案为:15.
19.解:如图,∵AB=AC,∠B=35°,
∴∠B=∠C=35°,
∴∠BAC=110°,
当∠BAD=90°时,
∠DAC=110°﹣90°=20°;
当∠ADB=90°时,
∵AB=AC,AD⊥BC,
∴∠DAC=∠BAD=55°.
故答案为:20°或55°.
20.解:如图,
根据已知,∠ACB=90°,AC=BC=6,点D在CA上,且DC=2,
∴AD=AC﹣CD=4,∠BAC=45°,
①作DP1⊥AB于P1,则三角形AP1D是等腰三角形;
②当AP2=AD=4时,三角形AP2D是等腰三角形;
③作DP3⊥AC,垂足为D,交AB于P3,则三角形AP3D是等腰三角形;
④当点P在BC上,AD=PD=4时,三角形AP4D是等腰三角形.
故使△APD为等腰三角形的点P有4个.
故答案为:4.
21.解:根据三角形三边关系,能摆成两种不同的等腰三角形,分别为:
①腰和底边都由3根火柴棒组成;②腰由4根火柴棒组成,底边有1根火柴棒,
故答案为:2.
22.解:∵CD平分∠ACB交AB于D,
∴∠ACD=∠DCB,
∵DE∥BC,
∴∠EDC=∠DCB,
∴∠EDC=∠ECD,
∴DE=EC=4cm,
∵AE=5cm,
∴AC=AE+EC=5+4=9(cm).
故答案为:9cm.
23.解:∵∠NPM=180°﹣70°﹣40°=70°,
∵向北的方向线是平行的,
∴∠M=70°,
∴∠NPM=∠M,
∴NP=MN=40×2=80(海里),
故答案为:80.
24.解:在△ABC中,∠C=90°,
则∠A+∠B=90°,
由题意得,
解得:∠A=60°,∠B=30°,
故答案为:60°.
25.解:∵∠B=90°,∠ACD=130°,∠A+∠B=∠ACD,
∴∠A=∠ACD﹣∠B=130°﹣90°=40°,
故答案为:40.
26.解:当腰为6时,则另两边长为6、20﹣6×2=8,此时三边满足三角形三边关系,即此时三角形的另两边为6,8;
当底边为6时,则另两边长为(20﹣6)=7,此时三边满足三角形三边关系,即此时三角形的另两边为7,7;
综上可知三角形的另两边长为6,8或7,7.
27.证明:∵AB∥CD,
∴∠DFE=∠1=60°,
∴∠CFE=180°﹣∠DFE,
=180°﹣60°,
=120°,
∴∠CEF=180°﹣∠2﹣∠CFE
=180°﹣30°﹣120°
=30°,
∴∠2=∠CEF,
∴CF=EF,
∴△FCE是等腰三角形.
28.解:(1)∵BO平分∠ABC,CO平分∠ACB,
∴∠PBO=∠CBO,∠QCO=∠BCO,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣∠A)==55°,
∴∠BOC=180°﹣55°=125°;
(2)∵PQ∥BC,
∴∠POB=∠PBO,
∴PB=PO,
同理可得QO=QC,
∴△APQ的周长为AP+PO+AQ+QO=AB+AC,
又∵△ABC的周长为32,BC=13,
∴AB+AC=32﹣13=19,
∴△APQ的周长为19.
29.解:∵∠C=90°,
∴∠CAB+∠CBA=90°,
∵BO、AO分别平分∠CBA、∠CAB,
∴∠2=∠CBA,∠1=∠CAB,
∴∠1+∠2=∠CBA+∠CAB=(∠CBA+∠CAB)=×90°=45°,
∴∠AOB=180°﹣(∠1+∠2)=180°﹣45°=135°.
30.解:(1)如图1,当点P在边AB的垂直平分线上时,
过点P作PD⊥AB于点D,连接BP,则PA=PB=t(cm),
∵∠ACB=90°,AB=10cm,BC=6cm,
∴AC=8cm,
∴PC=(8﹣t)cm,
在Rt△PCB中,由勾股定理得:PC2+BC2=PB2,即(8﹣t)2+62=t2,
解得:,
∴点P在AB边的垂直平分线上时,求t的值为.
(2)当点P在BC上时,
如图2,过点P作PE⊥AB,
∵AP平分∠BAC且PC⊥AC,
∴PC=PE=(t﹣8)cm,
∴PB=(14﹣t)cm,
在△ACP与△AEP中,
,
∴△ACP≌△AEP(AAS),
∴AE=AC=8cm,
∴BE=AB﹣AE=10﹣8=2cm,
在Rt△PEB中,由勾股定理得:PE2+EB2=PB2,
∴(t﹣8)2+22=(14﹣t)2,
解得:,
∴当点P在∠BAC的平分线上时,t的值为.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
