2021-2022学年北师大版九年级数学下册第三章圆解答题提升训练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第三章圆解答题提升训练(Word版,附答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 540.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 14:22:58 | ||
图片预览

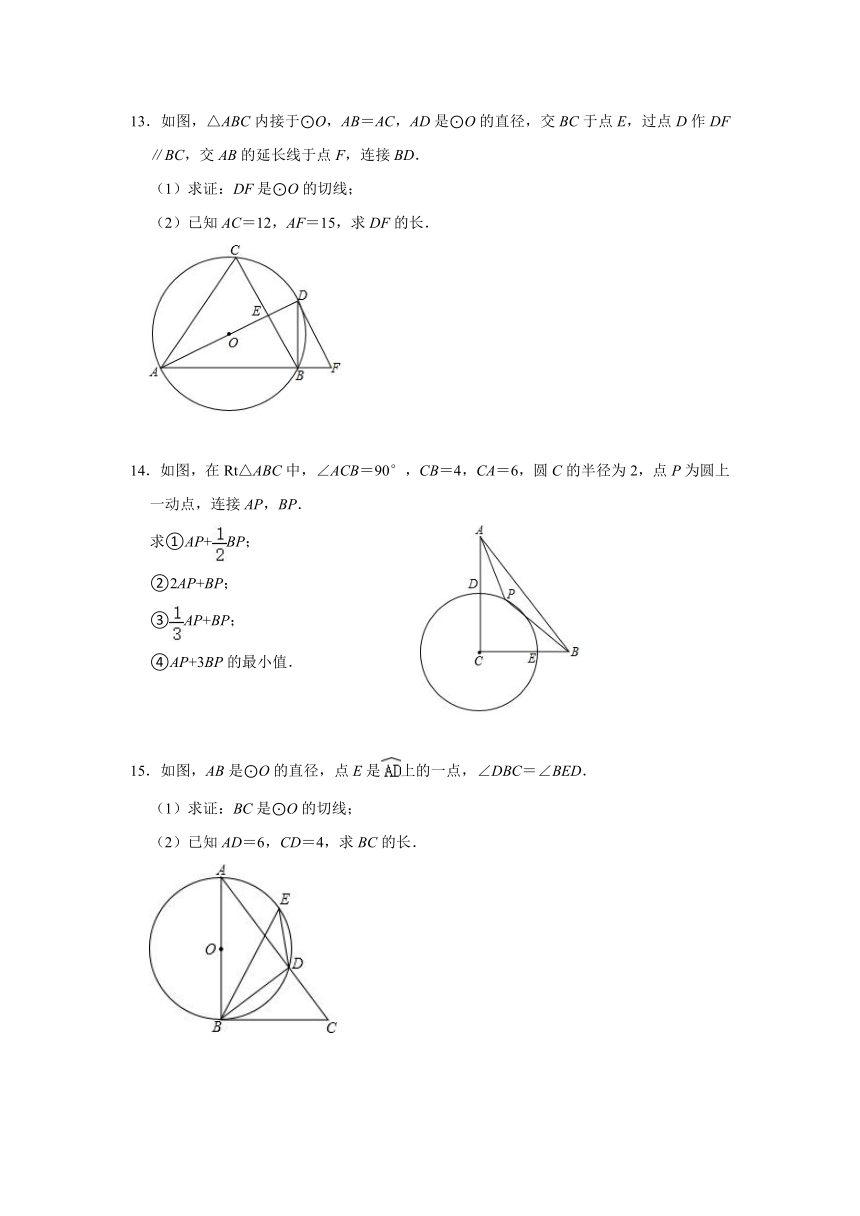
文档简介
2021-2022学年北师大版九年级数学下册《第3章圆》综合性解答题专题提升训练(附答案)
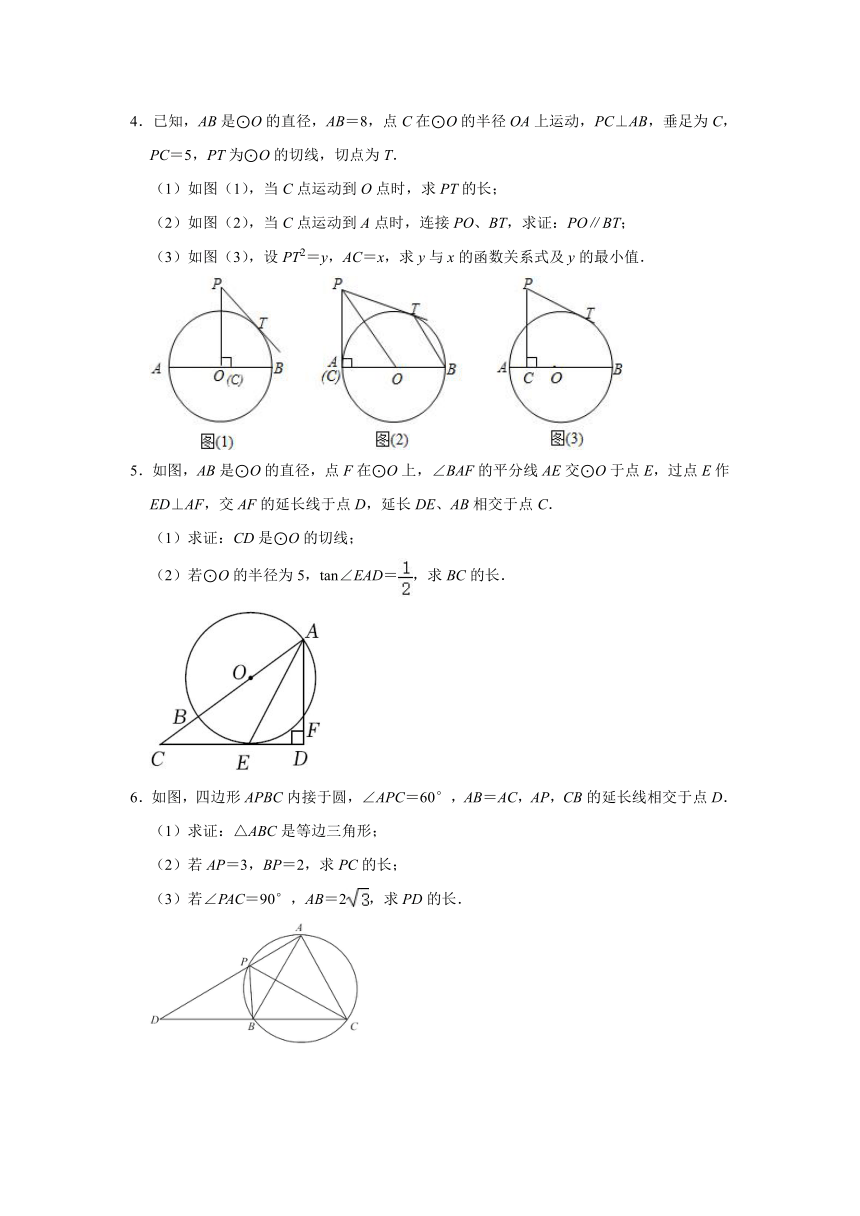
1.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)如果∠A=60°,则DE与DF有何数量关系?请说明理由;
(3)如果AB=5,BC=6,求tan∠BAC的值.
2.如图,AB是⊙O的直径,CD是⊙O的切线,切点为C.延长AB交CD于点E.连接AC,作∠DAC=∠ACD,作AF⊥ED于点F,交⊙O于点G.
(1)求证:AD是⊙O的切线;
(2)如果⊙O的半径是6cm,EC=8cm,求GF的长.
3.如图1,∠ABC=90°,AB=2,点D为BC边上的一个动点,连接AD,将△ABD沿AD翻折得到△AED,过点E作EF⊥BC于F.
(1)当BD=时,判断直线EF与以AD为直径的⊙O的位置关系,并加以证明;
(2)如图2,点D在BC上向点B运动,直线EF与以AD为直径的⊙O交于E、G两点,连接AG,当∠EAG=∠DAE时,求BD的长.
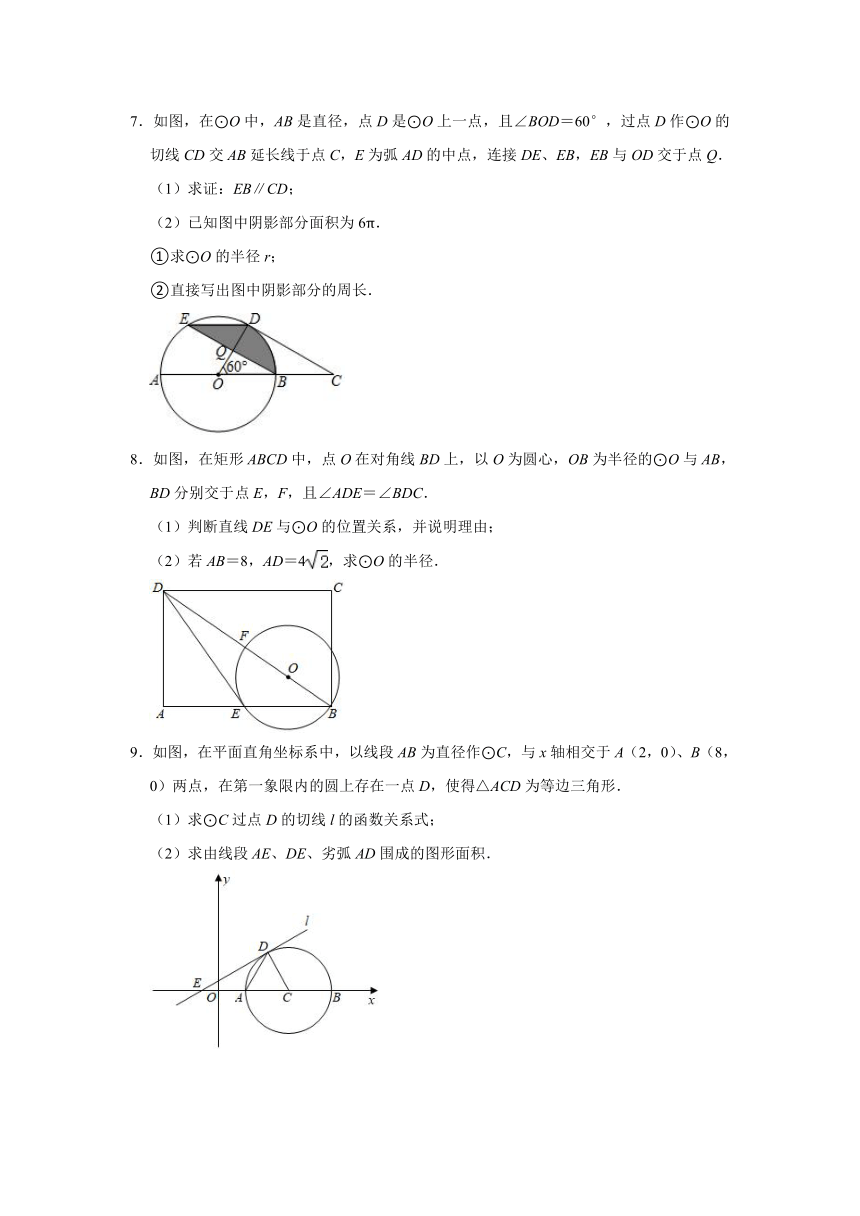
4.已知,AB是⊙O的直径,AB=8,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=5,PT为⊙O的切线,切点为T.
(1)如图(1),当C点运动到O点时,求PT的长;
(2)如图(2),当C点运动到A点时,连接PO、BT,求证:PO∥BT;
(3)如图(3),设PT2=y,AC=x,求y与x的函数关系式及y的最小值.
5.如图,AB是⊙O的直径,点F在⊙O上,∠BAF的平分线AE交⊙O于点E,过点E作ED⊥AF,交AF的延长线于点D,延长DE、AB相交于点C.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为5,tan∠EAD=,求BC的长.
6.如图,四边形APBC内接于圆,∠APC=60°,AB=AC,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若AP=3,BP=2,求PC的长;
(3)若∠PAC=90°,AB=2,求PD的长.
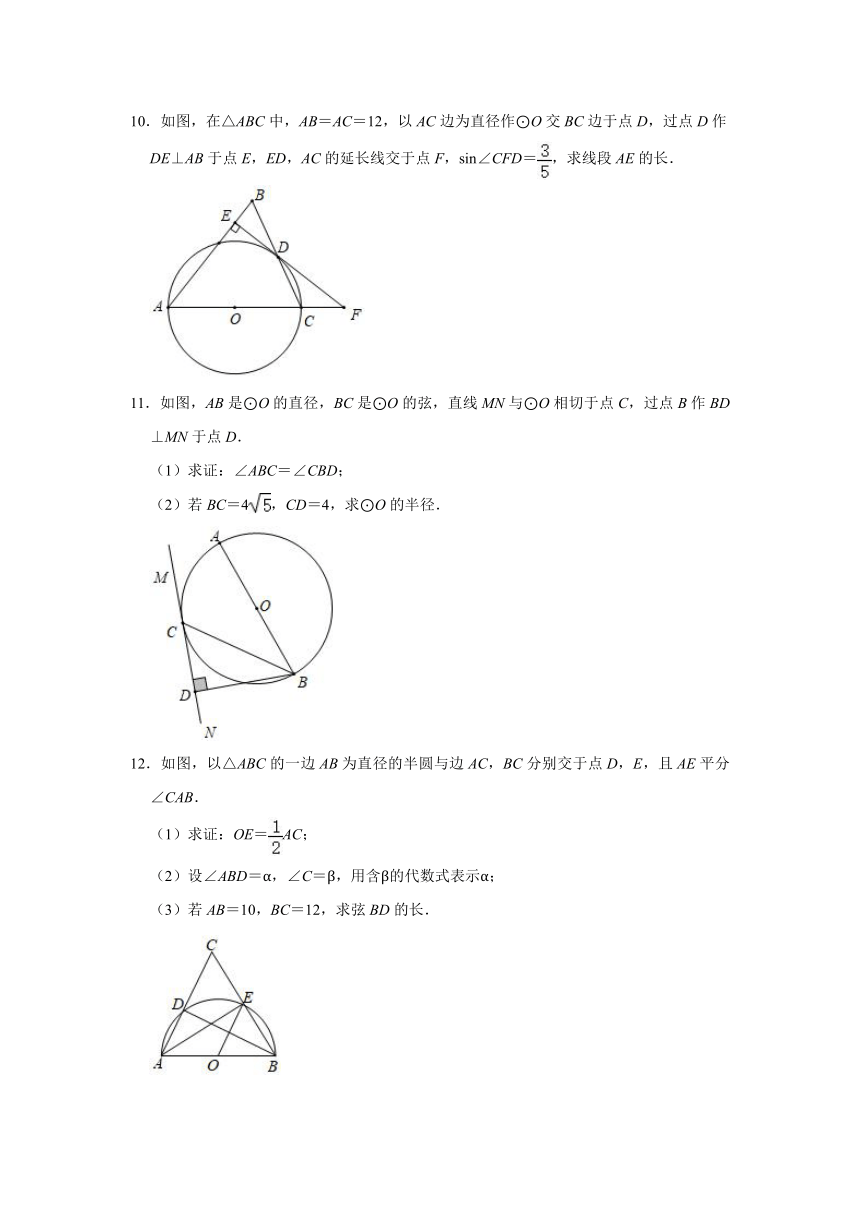
7.如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB延长线于点C,E为弧AD的中点,连接DE、EB,EB与OD交于点Q.
(1)求证:EB∥CD;
(2)已知图中阴影部分面积为6π.
①求⊙O的半径r;
②直接写出图中阴影部分的周长.
8.如图,在矩形ABCD中,点O在对角线BD上,以O为圆心,OB为半径的⊙O与AB,BD分别交于点E,F,且∠ADE=∠BDC.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AB=8,AD=4,求⊙O的半径.
9.如图,在平面直角坐标系中,以线段AB为直径作⊙C,与x轴相交于A(2,0)、B(8,0)两点,在第一象限内的圆上存在一点D,使得△ACD为等边三角形.
(1)求⊙C过点D的切线l的函数关系式;
(2)求由线段AE、DE、劣弧AD围成的图形面积.
10.如图,在△ABC中,AB=AC=12,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED,AC的延长线交于点F,sin∠CFD=,求线段AE的长.
11.如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.
(1)求证:∠ABC=∠CBD;
(2)若BC=4,CD=4,求⊙O的半径.
12.如图,以△ABC的一边AB为直径的半圆与边AC,BC分别交于点D,E,且AE平分∠CAB.
(1)求证:OE=AC;
(2)设∠ABD=α,∠C=β,用含β的代数式表示α;
(3)若AB=10,BC=12,求弦BD的长.
13.如图,△ABC内接于⊙O,AB=AC,AD是⊙O的直径,交BC于点E,过点D作DF∥BC,交AB的延长线于点F,连接BD.
(1)求证:DF是⊙O的切线;
(2)已知AC=12,AF=15,求DF的长.
14.如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,圆C的半径为2,点P为圆上一动点,连接AP,BP.
求①AP+BP;
②2AP+BP;
③AP+BP;
④AP+3BP的最小值.
15.如图,AB是⊙O的直径,点E是上的一点,∠DBC=∠BED.
(1)求证:BC是⊙O的切线;
(2)已知AD=6,CD=4,求BC的长.
16.如图,四边形ABCD内接于⊙O,对角线BD为⊙O直径,点E在BC延长线上,且∠E=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=16,DE=4,求⊙O半径的长.
17.如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)若AB=6,BD=5,求CP的长.
18.如图,Rt△ABC中,∠ACB=90°,点D在边AC上,以AD为直径作⊙O交BD的延长线于点E,交AB于点F,CE=BC.连接EF交AD于点G.
(1)求证:CE是⊙O的切线.
(2)若CD=2,BD=,求⊙O的半径,EG的长.
19.如图,已知△ABC内接于⊙O,AB为直径,∠ACB的平分线CD交⊙O于点D.点E为CA延长线上的一点,且∠ADE=∠BCD.
(1)判断DE与⊙O的位置关系,并说明理由.
(2)若⊙O的半径为2cm,且AB=2BC,求阴影部分的面积.
20.如图,△ABC内接于⊙O,AB是⊙O的直径,E为AB上一点,BE=BC,延长CE交AD于点D,AD=AC.
(1)求证:AD是⊙O的切线;
(2)若tan∠ACE=,OE=3,求BC的长.
参考答案
1.(1)证明:连接OD,
∵AB=AC,∴∠2=∠C,
∵OD=OB,∴∠2=∠1,
∴∠1=∠C,
∴OD∥AC,
∵EF⊥AC,
∴OD⊥EF,
∵点D在⊙O上,
∴EF是⊙O的切线;
(2)解:DE与DF的数量关系是DF=2DE.连接AD,
∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,∴∠3=∠4=∠BAC=×60°=30°,
∵∠F=90°﹣∠BAC=90°﹣60°=30°,
∴∠3=∠F,∴AD=DF,
∵∠4=30°,EF⊥AC,
∴DE=AD,∴DF=2DE;
(3)解:设⊙O与AC的交点为P,连接BP,
∵AB为直径,∴BP⊥AC,由上知BD=BC=×6=3,
∴AD===4,
S△ABC=BC AD=AC BP,
∴×6×4=×5×BP,
∴BP=,
∴直角△ABP中,AP===,
∴tan∠BAC===.
2.(1)证明:连接OC.
∵CD是⊙O的切线,
∴∠OCD=90°.
∴∠OCA+∠ACD=90°.
∵OA=OC,
∴∠OCA=∠OAC.
∵∠DAC=∠ACD,∠OCA+∠DAC=90°
∴∠0AC+∠CAD=90°.
∴∠OAD=90°.
∴AD是⊙O的切线.
(2)解:连接BG;
∵OC=6cm,EC=8cm,
∴在Rt△CEO中,OE==10.
∴AE=OE+OA=16.
∵AF⊥ED,
∴∠AFE=∠OCE=90°,∠E=∠E.
∴Rt△AEF∽Rt△OEC.
∴=.
即:=.
∴AF=9.6.
∵AB是⊙O的直径,
∴∠AGB=90°.
∴∠AGB=∠AFE.
∵∠BAG=∠EAF,
∴Rt△ABG∽Rt△AEF.
∴=.
即:=.
∴AG=7.2.
∴GF=AF﹣AG=9.6﹣7.2=2.4(cm).
3.解:(1)判断:直线EF与以AD为直径的⊙O相切;
证明:如图1,
作以AD为直径的⊙O,
∵将△ABD沿AD翻折得到△AED,
∴△ADB≌△ADE,
∴∠ABD=∠AED=90°,
∴点B和E都在⊙O上,
∵O为AD的中点,连接EO,
∴OE=OD=AD,
在Rt△ADB中,BD=,AB=2,
∴tan∠DAB==,
∴∠DAB=∠DAE=30°,
∴∠ADE=∠DOE=60°,
∴△DOE是等边三角形,
∴∠OED=60°,
∵∠EDF=180°﹣60°﹣60°=60°,
∴∠FDE=∠OED,
∴BF∥OE,
∵EF⊥BF,
∴OE⊥EF,且OE是⊙O的半径,
∴EF为⊙O的切线;
(2)如图2,延长AE交BC于点H,
∵∠AED=∠ABD=90°,
∴四边形AEDB是圆内接四边形,
∴∠FDE=∠BAE=∠EAD+∠DAB,
同理∠FED=∠EAD+∠GAE,
∵∠GAE=∠EAD=∠DAB,
∴∠FDE=∠FED,
又∠DFE=90°,
∴∠FDE=∠BAE=45°,
∴AB=BH=2,
设BD=x,则BD=DE=x,
∵∠DEH=90°,
∴DH=x,
∵DH+BD=BH,
∴x+x=2,
解得x=2﹣2,
∴BD=2﹣2.
4.(1)解:连接OT
∵PC=5,OT=4,
∴由勾股定理得,PT===3;
(2)证明:连接OT,∵PT,PC为⊙O的切线,
∴OP平分劣弧AT,
∴∠POA=∠POT,
∵∠AOT=2∠B,
∴∠AOP=∠B,
∴PO∥BT;
(3)解:设PC交⊙O于点D,延长线交⊙O于点E,
由相交弦定理,得CD2=AC BC,
∵AC=x,∴BC=8﹣x,
∴CD=,
∴由切割线定理,得PT2=PD PE,
∵PT2=y,PC=5,
∴y=[5﹣][5+],
∴y=25﹣x(8﹣x)=x2﹣8x+25,
∴y最小==9.
5.解:(1)连接OE,
∵OA=OE,
∴∠OAE=∠OEA,
∵AE平分∠BAF,
∴∠OAE=∠DAE,
∴∠OEA=∠EAD,
∴OE∥AD,
∵ED⊥AF,
∴OE⊥DE,
∴CD是⊙O的切线;
(2)连接BE,∵AB是⊙O的直径,
∴∠AEB=90°=∠D,
又∠DAE=∠BAE,
∴△ADE∽△AEB,
∴,
又tan∠EAD=,
∴,
则AE=2BE,又AB=10,
在△ABE中,AE2+BE2=AB2,
即(2BE)2+BE2=102,
解得:BE=,则AE=,
∴,
解得:AD=8,DE=4,
∵OE∥AD,
∴△COE∽△CAD,
∴,
设BC=x,
∴,
解得:x=,
经检验:x=是原方程的解,
故BC的长为.
6.(1)证明:∵∠APC=60°,
∴∠ABC=∠APC=60°,
∵AB=AC,
∴△ABC是等边三角形;
(2)解:如图1中,在PC上截取PT,使得PT=PA.
∵∠APT=60°,
∴△APT是等边三角形,
∵△ABC是等边三角形,
∴AP=AT,AB=AC,∠PAT=∠BAC=60°,
∴∠PAB=∠TAC,
∴△PAB≌△TAC(SAS),
∴PB=TC=2,
∵PT=PA=3,
∴PC=PT+CT=3+2=5;
(3)解:在Rt△PAC中,∠APC=60°,∠PAC=90°,AC=AB=2,
∴∠PCA=30°,
∴PC=2PA.
∵PC2=PA2+AC2,
∴PA=2,PC=4.
同理,可求出CD=4,AD=6,
∴PD=AD﹣PA=4.
7.(1)证明:连接OE,
∵CD是⊙O的切线,
∴OD⊥CD,即∠ODC=90°,
∵AB是⊙O的直径,∠BOD=60°,E为的中点,
∴∠EOD=60°=∠BOD,
∵OE=OB,
∴OD⊥BE,
∵OD⊥DC,
∴EB∥CD;
(2)解:①∵∠EOD=60°,OE=OD,
∴△EOD是等边三角形,
∴DE=OD=OB,∠EDQ=60°=∠BOD,
在△EQD和△BQO中,
,
∴△EQD≌△BQO(AAS),
∴S△EQD=S△BQO,
∴阴影部分的面积=扇形BOD的面积,
∵图中阴影部分面积为6π,
∴=6π,
解得:OB=6,
即⊙O的半径是6;
②∵OB=6,∠BOD=60°,∠OQB=90°,
∴OQ=OB==3,
∴BQ===3,
∵OD⊥BE,OD过O,
∴EQ=BQ=3,
∴BE=6,
的长是=2π,
∵DE=OB=6,
∴阴影部分的周长是BE+DE+的长=6+6+2π.
8.解:(1)直线DE与⊙O相切.
理由如下:连接OE,
∵四边形ABCD是矩形,
∴∠A=∠C=90°,DE∥AB,
∴∠BDC=∠OBE,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠BDC=∠OEB,
∵∠ADE=∠BDC,
∴∠ADE=∠OEB,
∵∠ADE+∠AED=90°,
∴∠OEB+∠AED=90°,
∴∠OEB+∠AED=90°,
∴∠DEO=180°﹣90°=90°,
即OE⊥DE,
∴直线DE与⊙O相切;
(2)∵四边形ABCD是矩形,
∴∠A=∠C=90°,AD=BC=4,AB=CD=8,
∵∠ADE=∠BDC,
∴△DAE∽△DCB,
∴=,
∴=,
∴AE=4,
∴BE=AB﹣AE=4,
过点O作OH⊥EB于点H,则EH=BH=2,
∵tan∠ABD==,
∴OH==,
在Rt△OBH中,OB===,
∴⊙O的半径为.
9.解:(1)∵A(2,0)、B(8,0),
∴AB=6,
∵以线段AB为直径作⊙C,
∴AC=3,
∵△ACD为等边三角形.,
∴CD=3,∠DCA=∠DAC=60°,
∵l是圆C过点D的切线,
∴∠CDE=90°,
∴∠DEC=30°,
∴∠DEA=30°,
∴AE=AD=3,
∴E(﹣1,0),
∵AC=3,A(2,0),
∴C(5,0),
过点D作DG⊥x轴,交于点G,
在Rt△AGD中,DG=AD sin60°=3×=,
AG=AD cos60°=3×=,
∴D(,),
设直线l的解析式为y=kx+b,
则,
∴,
∴y=x+;
(2)∵A(2,0),E(﹣1,0),D(,),C(5,0),
∴CD=3,ED=3,
∴S△CDE=×DE×DE=×3×3=,
∵∠ACD=60°,
∴S扇形ACD==,
∴线段AE、DE、劣弧AD围成的图形面积为﹣.
10.解:连接OD,如图,
∵AB=AC,
∴∠B=∠ACD,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠B=∠ODC,
∴OD∥AB,
∵DE⊥AB
∴OD⊥EF,
∴∠ODF=90°
∵AB=AC=12,
∴OA=OC=OD=6,
在Rt△ODF,sin∠OFD==,
∴OF=10,
∴AF=16,
在Rt△AEF中,∵sin∠AFE==,
∴AE=×16=.
11.(1)证明:连接OC,
∵MN为⊙O的切线,
∴OC⊥MN,
∵BD⊥MN,
∴OC∥BD,
∴∠CBD=∠BCO.
又∵OC=OB,
∴∠BCO=∠ABC,
∴∠CBD=∠ABC;
(2)解:连接AC,
在Rt△BCD中,BC=4,CD=4,
∴BD==8,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠CDB=90°,
∵∠ABC=∠CBD,
∴△ABC∽△CBD,
∴,即,
∴AB=10,
∴⊙O的半径是5.
12.(1)证明:∵AB是直径,
∴∠AEB=90°,
∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵∠C+∠CAE=90°,∠ABE+∠BAE=90°,
∴∠C=∠ABC,
∴AC=AB,
∵AE⊥BC,
∴EC=EB,
∴OA=OB,
∴OE=AC.
(2)解:∵AB是直径,
∴∠ADB=90°,
∴∠CAB=90°﹣∠ABD=90°﹣α,
∵∠C+∠ABC+∠CAB=180°,
∴2β+90°﹣α=180°,
∴2β﹣α=90°,
即α=2β﹣90°.
(3)解:∵EC=EB=BC=6,AB=10,∠AEB=90°,
∴AE===8,
∵BD⊥AC,AE⊥BC,
∴S△ABC= AC BD= BC AE,
∴BD==.
13.(1)证明:∵AD是⊙O的直径,
∴∠ABD=90°,
即∠ABC+∠CBD=90°,
∵AB=AC,
∴∠ABC=∠C,
∵∠ADB=∠C,
∴∠ABC=∠ADB,
∵BC∥DF,
∴∠CBD=∠FDB,
∴∠ADB+∠FDB=90°,
即∠ADF=90°,
∴AD⊥DF,
又∵OD是⊙O的半径,
∴DF是⊙O的切线;
(2)解:∵AB=AC=12,AF=15,
∴BF=AF﹣AB=3,
∵∠F=∠F,∠FBD=∠FDA=90°,
∴△FBD∽△FDA,
∴BF:DF=DF:AF,
∴DF2=BF×AF=3×15=45,
∴DF==3.
14.解:①取CE的中点F,连结PF,AF,
∵CF=1,CB=4,CP=2,
∴,
∵∠PCF=∠BCP,
∴△PCF∽△BCP,
∴,
∴,
∴,
=AP+PF,
当P在AF上时,AP+PF最小,
最小值为AF的长,
,
=,
的最小值为,
②∵2AP+BP=2,
∴2AP+BP的最小值为,
③在DC取一点G,使CG=
∵,
∴,
∵∠ACP=∠PCG,
∴△CGP∽△CPA,
∴,
∴,
∴,
=GP+BP BG,
当P在BG上B,
GP+BP=BG,
=
=,
∴的最小值为,
④∵,
∴AP+3BP的最小值为.
15.解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ABD+∠BAD=90°,
∵∠DBC=∠BED=∠BAD,
∴∠ABD+∠DBC=90°,
∵OB是⊙O的半径,
∴BC是⊙O的切线;
(2)∵BC是⊙O的切线,
∴∠OBC=90°,
∵∠DBC=∠BAC,∠C=∠C,
∴△ABC∽△BDC,
∴=,
∴BC2=AC CD,
即BC2=(6+4)×4=40,
∴BC==2.
16.(1)证明:∵BD为⊙O的直径,
∴∠BCD=∠DCE=90°,
∴∠E+∠CDE=90°,
∵∠E=∠BAC,
∴∠BAC+∠CDE=90°,
∵∠BAC=∠BDC,
∴∠BDC+∠CDE=90°,即∠BDE=90°,
∴BD⊥DE,
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)解:∵AC∥DE,
∴∠E=∠ACB,
∵∠E=∠BAC,
∴∠ACB=∠BAC,
∴BC=AB=16,
由(1)可得:∠BDC+∠CDE=90°,
∵∠BDC+∠CBD=90°,
∴∠CDE=∠CBD,
∵∠DCE=∠BCD=90°,
∴△CDE∽△DBE,
∴,
∵BE=BC+CE,AB=16,DE=4,
∴,解得CE=4,
在Rt△CDE中,CD==8,
在Rt△BCD中,BD==8,
∴OB=BD=4.
17.解:(1)连接OD,
∵圆心O在BC上,
∴BC为直径,
∴∠BAC=∠BDC=90°,
∵AD平分∠BAC,
∴∠BAD=∠BAC=45°,
∴∠BOD=2∠BAD=90°,
∵BC∥DP,
∴∠ODP=∠BOD=90°,
∵OD为半径,
∴DP是⊙O的切线;
(2)∵∠BDC=90°,∠BCD=45°,
∴∠BCD=∠DBC=45°,
∴BD=CD=5,
∵四边形ABDC内接于⊙O,
∴∠ABD=∠PCD,
∴∠BAD=∠CAD=∠CDP=45°,
∴△ABD∽△DCP,
∴=,
即=,
∴CP=,
18.解:(1)如图,连接OE,
∵∠ACB=90°,
∴∠CBD+∠BDC=90°,
∵CE=BC,
∴∠CBD=∠BEC,
∵OE=OD,
∴∠OED=∠ODE,
又∵∠BDC=∠ODE,
∴∠OED=∠BDC,
∴∠OED+∠BEC=90°,即∠OEC=90°,
∴OE⊥CE.
∵OE是⊙O的半径,
∴CE是⊙O的切线;
(2)在Rt△BCD中,∠DCB=90°,CD=2,BD=2,
BC==4=CE,
设⊙O的半径为r,则OD=OE=r,OC=r+2,
在Rt△OEC中,∠OEC=90°,
∴OE2+CE2=OC2,
∴即r2+42=(r+2)2,
解得r=3,
∴⊙O的半径为3;
连接DF、AE,
∵AD是⊙O的直径,
∴∠AFD=∠AED=90°,
∵tan∠BAC====,
在Rt△ADF中,AD=6,
∴DF==,AF=,
又∵EC是⊙O的切线,DE是弦,
∴∠DEC=∠EAC,
又∵∠DCE=∠ECA,
∴△DEC∽△EAC,
∴===,
在Rt△AED中,AD=6,
∴DE===DF,AE==AF,
∴EF⊥AD,
在Rt△ADE中,由面积公式得,
DE AE=AD EG
即×=6EG,
∴EG=,
∴⊙O的半径为3,EG的长为.
19.解:(1)DE与⊙O相切;
理由:连接OD,BD,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴=,
∴BD=AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB=∠ABD=45°,
∵AO=BO,
∴∠ADO=45°,
∵∠ADE=∠BCD=∠DAB=45°,
∴∠ODE=90°,
∴DE与⊙O相切;
(2)连接OC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵AB=2BC,
∴∠BAC=30°,
∴∠ABC=60°,
∴∠AOC=2∠ABC=120°,
∵⊙O的半径为2cm,
∴AB=4cm,AC=2cm,
∴阴影部分的面积=S扇形AOC﹣S△AOC=﹣1×2=﹣.
20.解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
即∠ACE+∠BCE=90°,
∵AD=AC,BE=BC,
∴∠ACE=∠D,∠BCE=∠BEC,
又∵∠BEC=∠AED,
∴∠AED+∠D=90°,
∴∠DAE=90°,
即AD⊥AE,
∵OA是半径,
∴AD是⊙O的切线;
(2)由tan∠ACE==tan∠D可设AE=a,则AD=3a=AC,
∵OE=3,
∴OA=a+3,AB=2a+6,
∴BE=a+3+3=a+6=BC,
在Rt△ABC中,由勾股定理得,
AB2=BC2+AC2,
即(2a+6)2=(a+6)2+(3a)2,
解得a1=0(舍去),a2=2,
∴BC=a+6=8.
1.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)如果∠A=60°,则DE与DF有何数量关系?请说明理由;
(3)如果AB=5,BC=6,求tan∠BAC的值.
2.如图,AB是⊙O的直径,CD是⊙O的切线,切点为C.延长AB交CD于点E.连接AC,作∠DAC=∠ACD,作AF⊥ED于点F,交⊙O于点G.
(1)求证:AD是⊙O的切线;
(2)如果⊙O的半径是6cm,EC=8cm,求GF的长.
3.如图1,∠ABC=90°,AB=2,点D为BC边上的一个动点,连接AD,将△ABD沿AD翻折得到△AED,过点E作EF⊥BC于F.
(1)当BD=时,判断直线EF与以AD为直径的⊙O的位置关系,并加以证明;
(2)如图2,点D在BC上向点B运动,直线EF与以AD为直径的⊙O交于E、G两点,连接AG,当∠EAG=∠DAE时,求BD的长.
4.已知,AB是⊙O的直径,AB=8,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=5,PT为⊙O的切线,切点为T.
(1)如图(1),当C点运动到O点时,求PT的长;
(2)如图(2),当C点运动到A点时,连接PO、BT,求证:PO∥BT;
(3)如图(3),设PT2=y,AC=x,求y与x的函数关系式及y的最小值.
5.如图,AB是⊙O的直径,点F在⊙O上,∠BAF的平分线AE交⊙O于点E,过点E作ED⊥AF,交AF的延长线于点D,延长DE、AB相交于点C.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为5,tan∠EAD=,求BC的长.
6.如图,四边形APBC内接于圆,∠APC=60°,AB=AC,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若AP=3,BP=2,求PC的长;
(3)若∠PAC=90°,AB=2,求PD的长.
7.如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB延长线于点C,E为弧AD的中点,连接DE、EB,EB与OD交于点Q.
(1)求证:EB∥CD;
(2)已知图中阴影部分面积为6π.
①求⊙O的半径r;
②直接写出图中阴影部分的周长.
8.如图,在矩形ABCD中,点O在对角线BD上,以O为圆心,OB为半径的⊙O与AB,BD分别交于点E,F,且∠ADE=∠BDC.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AB=8,AD=4,求⊙O的半径.
9.如图,在平面直角坐标系中,以线段AB为直径作⊙C,与x轴相交于A(2,0)、B(8,0)两点,在第一象限内的圆上存在一点D,使得△ACD为等边三角形.
(1)求⊙C过点D的切线l的函数关系式;
(2)求由线段AE、DE、劣弧AD围成的图形面积.
10.如图,在△ABC中,AB=AC=12,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED,AC的延长线交于点F,sin∠CFD=,求线段AE的长.
11.如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.
(1)求证:∠ABC=∠CBD;
(2)若BC=4,CD=4,求⊙O的半径.
12.如图,以△ABC的一边AB为直径的半圆与边AC,BC分别交于点D,E,且AE平分∠CAB.
(1)求证:OE=AC;
(2)设∠ABD=α,∠C=β,用含β的代数式表示α;
(3)若AB=10,BC=12,求弦BD的长.
13.如图,△ABC内接于⊙O,AB=AC,AD是⊙O的直径,交BC于点E,过点D作DF∥BC,交AB的延长线于点F,连接BD.
(1)求证:DF是⊙O的切线;
(2)已知AC=12,AF=15,求DF的长.
14.如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,圆C的半径为2,点P为圆上一动点,连接AP,BP.
求①AP+BP;
②2AP+BP;
③AP+BP;
④AP+3BP的最小值.
15.如图,AB是⊙O的直径,点E是上的一点,∠DBC=∠BED.
(1)求证:BC是⊙O的切线;
(2)已知AD=6,CD=4,求BC的长.
16.如图,四边形ABCD内接于⊙O,对角线BD为⊙O直径,点E在BC延长线上,且∠E=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=16,DE=4,求⊙O半径的长.
17.如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)若AB=6,BD=5,求CP的长.
18.如图,Rt△ABC中,∠ACB=90°,点D在边AC上,以AD为直径作⊙O交BD的延长线于点E,交AB于点F,CE=BC.连接EF交AD于点G.
(1)求证:CE是⊙O的切线.
(2)若CD=2,BD=,求⊙O的半径,EG的长.
19.如图,已知△ABC内接于⊙O,AB为直径,∠ACB的平分线CD交⊙O于点D.点E为CA延长线上的一点,且∠ADE=∠BCD.
(1)判断DE与⊙O的位置关系,并说明理由.
(2)若⊙O的半径为2cm,且AB=2BC,求阴影部分的面积.
20.如图,△ABC内接于⊙O,AB是⊙O的直径,E为AB上一点,BE=BC,延长CE交AD于点D,AD=AC.
(1)求证:AD是⊙O的切线;
(2)若tan∠ACE=,OE=3,求BC的长.
参考答案
1.(1)证明:连接OD,
∵AB=AC,∴∠2=∠C,
∵OD=OB,∴∠2=∠1,
∴∠1=∠C,
∴OD∥AC,
∵EF⊥AC,
∴OD⊥EF,
∵点D在⊙O上,
∴EF是⊙O的切线;
(2)解:DE与DF的数量关系是DF=2DE.连接AD,
∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,∴∠3=∠4=∠BAC=×60°=30°,
∵∠F=90°﹣∠BAC=90°﹣60°=30°,
∴∠3=∠F,∴AD=DF,
∵∠4=30°,EF⊥AC,
∴DE=AD,∴DF=2DE;
(3)解:设⊙O与AC的交点为P,连接BP,
∵AB为直径,∴BP⊥AC,由上知BD=BC=×6=3,
∴AD===4,
S△ABC=BC AD=AC BP,
∴×6×4=×5×BP,
∴BP=,
∴直角△ABP中,AP===,
∴tan∠BAC===.
2.(1)证明:连接OC.
∵CD是⊙O的切线,
∴∠OCD=90°.
∴∠OCA+∠ACD=90°.
∵OA=OC,
∴∠OCA=∠OAC.
∵∠DAC=∠ACD,∠OCA+∠DAC=90°
∴∠0AC+∠CAD=90°.
∴∠OAD=90°.
∴AD是⊙O的切线.
(2)解:连接BG;
∵OC=6cm,EC=8cm,
∴在Rt△CEO中,OE==10.
∴AE=OE+OA=16.
∵AF⊥ED,
∴∠AFE=∠OCE=90°,∠E=∠E.
∴Rt△AEF∽Rt△OEC.
∴=.
即:=.
∴AF=9.6.
∵AB是⊙O的直径,
∴∠AGB=90°.
∴∠AGB=∠AFE.
∵∠BAG=∠EAF,
∴Rt△ABG∽Rt△AEF.
∴=.
即:=.
∴AG=7.2.
∴GF=AF﹣AG=9.6﹣7.2=2.4(cm).
3.解:(1)判断:直线EF与以AD为直径的⊙O相切;
证明:如图1,
作以AD为直径的⊙O,
∵将△ABD沿AD翻折得到△AED,
∴△ADB≌△ADE,
∴∠ABD=∠AED=90°,
∴点B和E都在⊙O上,
∵O为AD的中点,连接EO,
∴OE=OD=AD,
在Rt△ADB中,BD=,AB=2,
∴tan∠DAB==,
∴∠DAB=∠DAE=30°,
∴∠ADE=∠DOE=60°,
∴△DOE是等边三角形,
∴∠OED=60°,
∵∠EDF=180°﹣60°﹣60°=60°,
∴∠FDE=∠OED,
∴BF∥OE,
∵EF⊥BF,
∴OE⊥EF,且OE是⊙O的半径,
∴EF为⊙O的切线;
(2)如图2,延长AE交BC于点H,
∵∠AED=∠ABD=90°,
∴四边形AEDB是圆内接四边形,
∴∠FDE=∠BAE=∠EAD+∠DAB,
同理∠FED=∠EAD+∠GAE,
∵∠GAE=∠EAD=∠DAB,
∴∠FDE=∠FED,
又∠DFE=90°,
∴∠FDE=∠BAE=45°,
∴AB=BH=2,
设BD=x,则BD=DE=x,
∵∠DEH=90°,
∴DH=x,
∵DH+BD=BH,
∴x+x=2,
解得x=2﹣2,
∴BD=2﹣2.
4.(1)解:连接OT
∵PC=5,OT=4,
∴由勾股定理得,PT===3;
(2)证明:连接OT,∵PT,PC为⊙O的切线,
∴OP平分劣弧AT,
∴∠POA=∠POT,
∵∠AOT=2∠B,
∴∠AOP=∠B,
∴PO∥BT;
(3)解:设PC交⊙O于点D,延长线交⊙O于点E,
由相交弦定理,得CD2=AC BC,
∵AC=x,∴BC=8﹣x,
∴CD=,
∴由切割线定理,得PT2=PD PE,
∵PT2=y,PC=5,
∴y=[5﹣][5+],
∴y=25﹣x(8﹣x)=x2﹣8x+25,
∴y最小==9.
5.解:(1)连接OE,
∵OA=OE,
∴∠OAE=∠OEA,
∵AE平分∠BAF,
∴∠OAE=∠DAE,
∴∠OEA=∠EAD,
∴OE∥AD,
∵ED⊥AF,
∴OE⊥DE,
∴CD是⊙O的切线;
(2)连接BE,∵AB是⊙O的直径,
∴∠AEB=90°=∠D,
又∠DAE=∠BAE,
∴△ADE∽△AEB,
∴,
又tan∠EAD=,
∴,
则AE=2BE,又AB=10,
在△ABE中,AE2+BE2=AB2,
即(2BE)2+BE2=102,
解得:BE=,则AE=,
∴,
解得:AD=8,DE=4,
∵OE∥AD,
∴△COE∽△CAD,
∴,
设BC=x,
∴,
解得:x=,
经检验:x=是原方程的解,
故BC的长为.
6.(1)证明:∵∠APC=60°,
∴∠ABC=∠APC=60°,
∵AB=AC,
∴△ABC是等边三角形;
(2)解:如图1中,在PC上截取PT,使得PT=PA.
∵∠APT=60°,
∴△APT是等边三角形,
∵△ABC是等边三角形,
∴AP=AT,AB=AC,∠PAT=∠BAC=60°,
∴∠PAB=∠TAC,
∴△PAB≌△TAC(SAS),
∴PB=TC=2,
∵PT=PA=3,
∴PC=PT+CT=3+2=5;
(3)解:在Rt△PAC中,∠APC=60°,∠PAC=90°,AC=AB=2,
∴∠PCA=30°,
∴PC=2PA.
∵PC2=PA2+AC2,
∴PA=2,PC=4.
同理,可求出CD=4,AD=6,
∴PD=AD﹣PA=4.
7.(1)证明:连接OE,
∵CD是⊙O的切线,
∴OD⊥CD,即∠ODC=90°,
∵AB是⊙O的直径,∠BOD=60°,E为的中点,
∴∠EOD=60°=∠BOD,
∵OE=OB,
∴OD⊥BE,
∵OD⊥DC,
∴EB∥CD;
(2)解:①∵∠EOD=60°,OE=OD,
∴△EOD是等边三角形,
∴DE=OD=OB,∠EDQ=60°=∠BOD,
在△EQD和△BQO中,
,
∴△EQD≌△BQO(AAS),
∴S△EQD=S△BQO,
∴阴影部分的面积=扇形BOD的面积,
∵图中阴影部分面积为6π,
∴=6π,
解得:OB=6,
即⊙O的半径是6;
②∵OB=6,∠BOD=60°,∠OQB=90°,
∴OQ=OB==3,
∴BQ===3,
∵OD⊥BE,OD过O,
∴EQ=BQ=3,
∴BE=6,
的长是=2π,
∵DE=OB=6,
∴阴影部分的周长是BE+DE+的长=6+6+2π.
8.解:(1)直线DE与⊙O相切.
理由如下:连接OE,
∵四边形ABCD是矩形,
∴∠A=∠C=90°,DE∥AB,
∴∠BDC=∠OBE,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠BDC=∠OEB,
∵∠ADE=∠BDC,
∴∠ADE=∠OEB,
∵∠ADE+∠AED=90°,
∴∠OEB+∠AED=90°,
∴∠OEB+∠AED=90°,
∴∠DEO=180°﹣90°=90°,
即OE⊥DE,
∴直线DE与⊙O相切;
(2)∵四边形ABCD是矩形,
∴∠A=∠C=90°,AD=BC=4,AB=CD=8,
∵∠ADE=∠BDC,
∴△DAE∽△DCB,
∴=,
∴=,
∴AE=4,
∴BE=AB﹣AE=4,
过点O作OH⊥EB于点H,则EH=BH=2,
∵tan∠ABD==,
∴OH==,
在Rt△OBH中,OB===,
∴⊙O的半径为.
9.解:(1)∵A(2,0)、B(8,0),
∴AB=6,
∵以线段AB为直径作⊙C,
∴AC=3,
∵△ACD为等边三角形.,
∴CD=3,∠DCA=∠DAC=60°,
∵l是圆C过点D的切线,
∴∠CDE=90°,
∴∠DEC=30°,
∴∠DEA=30°,
∴AE=AD=3,
∴E(﹣1,0),
∵AC=3,A(2,0),
∴C(5,0),
过点D作DG⊥x轴,交于点G,
在Rt△AGD中,DG=AD sin60°=3×=,
AG=AD cos60°=3×=,
∴D(,),
设直线l的解析式为y=kx+b,
则,
∴,
∴y=x+;
(2)∵A(2,0),E(﹣1,0),D(,),C(5,0),
∴CD=3,ED=3,
∴S△CDE=×DE×DE=×3×3=,
∵∠ACD=60°,
∴S扇形ACD==,
∴线段AE、DE、劣弧AD围成的图形面积为﹣.
10.解:连接OD,如图,
∵AB=AC,
∴∠B=∠ACD,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠B=∠ODC,
∴OD∥AB,
∵DE⊥AB
∴OD⊥EF,
∴∠ODF=90°
∵AB=AC=12,
∴OA=OC=OD=6,
在Rt△ODF,sin∠OFD==,
∴OF=10,
∴AF=16,
在Rt△AEF中,∵sin∠AFE==,
∴AE=×16=.
11.(1)证明:连接OC,
∵MN为⊙O的切线,
∴OC⊥MN,
∵BD⊥MN,
∴OC∥BD,
∴∠CBD=∠BCO.
又∵OC=OB,
∴∠BCO=∠ABC,
∴∠CBD=∠ABC;
(2)解:连接AC,
在Rt△BCD中,BC=4,CD=4,
∴BD==8,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠CDB=90°,
∵∠ABC=∠CBD,
∴△ABC∽△CBD,
∴,即,
∴AB=10,
∴⊙O的半径是5.
12.(1)证明:∵AB是直径,
∴∠AEB=90°,
∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵∠C+∠CAE=90°,∠ABE+∠BAE=90°,
∴∠C=∠ABC,
∴AC=AB,
∵AE⊥BC,
∴EC=EB,
∴OA=OB,
∴OE=AC.
(2)解:∵AB是直径,
∴∠ADB=90°,
∴∠CAB=90°﹣∠ABD=90°﹣α,
∵∠C+∠ABC+∠CAB=180°,
∴2β+90°﹣α=180°,
∴2β﹣α=90°,
即α=2β﹣90°.
(3)解:∵EC=EB=BC=6,AB=10,∠AEB=90°,
∴AE===8,
∵BD⊥AC,AE⊥BC,
∴S△ABC= AC BD= BC AE,
∴BD==.
13.(1)证明:∵AD是⊙O的直径,
∴∠ABD=90°,
即∠ABC+∠CBD=90°,
∵AB=AC,
∴∠ABC=∠C,
∵∠ADB=∠C,
∴∠ABC=∠ADB,
∵BC∥DF,
∴∠CBD=∠FDB,
∴∠ADB+∠FDB=90°,
即∠ADF=90°,
∴AD⊥DF,
又∵OD是⊙O的半径,
∴DF是⊙O的切线;
(2)解:∵AB=AC=12,AF=15,
∴BF=AF﹣AB=3,
∵∠F=∠F,∠FBD=∠FDA=90°,
∴△FBD∽△FDA,
∴BF:DF=DF:AF,
∴DF2=BF×AF=3×15=45,
∴DF==3.
14.解:①取CE的中点F,连结PF,AF,
∵CF=1,CB=4,CP=2,
∴,
∵∠PCF=∠BCP,
∴△PCF∽△BCP,
∴,
∴,
∴,
=AP+PF,
当P在AF上时,AP+PF最小,
最小值为AF的长,
,
=,
的最小值为,
②∵2AP+BP=2,
∴2AP+BP的最小值为,
③在DC取一点G,使CG=
∵,
∴,
∵∠ACP=∠PCG,
∴△CGP∽△CPA,
∴,
∴,
∴,
=GP+BP BG,
当P在BG上B,
GP+BP=BG,
=
=,
∴的最小值为,
④∵,
∴AP+3BP的最小值为.
15.解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ABD+∠BAD=90°,
∵∠DBC=∠BED=∠BAD,
∴∠ABD+∠DBC=90°,
∵OB是⊙O的半径,
∴BC是⊙O的切线;
(2)∵BC是⊙O的切线,
∴∠OBC=90°,
∵∠DBC=∠BAC,∠C=∠C,
∴△ABC∽△BDC,
∴=,
∴BC2=AC CD,
即BC2=(6+4)×4=40,
∴BC==2.
16.(1)证明:∵BD为⊙O的直径,
∴∠BCD=∠DCE=90°,
∴∠E+∠CDE=90°,
∵∠E=∠BAC,
∴∠BAC+∠CDE=90°,
∵∠BAC=∠BDC,
∴∠BDC+∠CDE=90°,即∠BDE=90°,
∴BD⊥DE,
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)解:∵AC∥DE,
∴∠E=∠ACB,
∵∠E=∠BAC,
∴∠ACB=∠BAC,
∴BC=AB=16,
由(1)可得:∠BDC+∠CDE=90°,
∵∠BDC+∠CBD=90°,
∴∠CDE=∠CBD,
∵∠DCE=∠BCD=90°,
∴△CDE∽△DBE,
∴,
∵BE=BC+CE,AB=16,DE=4,
∴,解得CE=4,
在Rt△CDE中,CD==8,
在Rt△BCD中,BD==8,
∴OB=BD=4.
17.解:(1)连接OD,
∵圆心O在BC上,
∴BC为直径,
∴∠BAC=∠BDC=90°,
∵AD平分∠BAC,
∴∠BAD=∠BAC=45°,
∴∠BOD=2∠BAD=90°,
∵BC∥DP,
∴∠ODP=∠BOD=90°,
∵OD为半径,
∴DP是⊙O的切线;
(2)∵∠BDC=90°,∠BCD=45°,
∴∠BCD=∠DBC=45°,
∴BD=CD=5,
∵四边形ABDC内接于⊙O,
∴∠ABD=∠PCD,
∴∠BAD=∠CAD=∠CDP=45°,
∴△ABD∽△DCP,
∴=,
即=,
∴CP=,
18.解:(1)如图,连接OE,
∵∠ACB=90°,
∴∠CBD+∠BDC=90°,
∵CE=BC,
∴∠CBD=∠BEC,
∵OE=OD,
∴∠OED=∠ODE,
又∵∠BDC=∠ODE,
∴∠OED=∠BDC,
∴∠OED+∠BEC=90°,即∠OEC=90°,
∴OE⊥CE.
∵OE是⊙O的半径,
∴CE是⊙O的切线;
(2)在Rt△BCD中,∠DCB=90°,CD=2,BD=2,
BC==4=CE,
设⊙O的半径为r,则OD=OE=r,OC=r+2,
在Rt△OEC中,∠OEC=90°,
∴OE2+CE2=OC2,
∴即r2+42=(r+2)2,
解得r=3,
∴⊙O的半径为3;
连接DF、AE,
∵AD是⊙O的直径,
∴∠AFD=∠AED=90°,
∵tan∠BAC====,
在Rt△ADF中,AD=6,
∴DF==,AF=,
又∵EC是⊙O的切线,DE是弦,
∴∠DEC=∠EAC,
又∵∠DCE=∠ECA,
∴△DEC∽△EAC,
∴===,
在Rt△AED中,AD=6,
∴DE===DF,AE==AF,
∴EF⊥AD,
在Rt△ADE中,由面积公式得,
DE AE=AD EG
即×=6EG,
∴EG=,
∴⊙O的半径为3,EG的长为.
19.解:(1)DE与⊙O相切;
理由:连接OD,BD,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴=,
∴BD=AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB=∠ABD=45°,
∵AO=BO,
∴∠ADO=45°,
∵∠ADE=∠BCD=∠DAB=45°,
∴∠ODE=90°,
∴DE与⊙O相切;
(2)连接OC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵AB=2BC,
∴∠BAC=30°,
∴∠ABC=60°,
∴∠AOC=2∠ABC=120°,
∵⊙O的半径为2cm,
∴AB=4cm,AC=2cm,
∴阴影部分的面积=S扇形AOC﹣S△AOC=﹣1×2=﹣.
20.解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
即∠ACE+∠BCE=90°,
∵AD=AC,BE=BC,
∴∠ACE=∠D,∠BCE=∠BEC,
又∵∠BEC=∠AED,
∴∠AED+∠D=90°,
∴∠DAE=90°,
即AD⊥AE,
∵OA是半径,
∴AD是⊙O的切线;
(2)由tan∠ACE==tan∠D可设AE=a,则AD=3a=AC,
∵OE=3,
∴OA=a+3,AB=2a+6,
∴BE=a+3+3=a+6=BC,
在Rt△ABC中,由勾股定理得,
AB2=BC2+AC2,
即(2a+6)2=(a+6)2+(3a)2,
解得a1=0(舍去),a2=2,
∴BC=a+6=8.
