2021_2022学年数学京改版七年级下册第七章:观察、猜想与证明课后练习(word版含答案)
文档属性
| 名称 | 2021_2022学年数学京改版七年级下册第七章:观察、猜想与证明课后练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 335.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 21:08:07 | ||
图片预览



文档简介
第七章:观察、猜想与证明
一、选择题(共15题)
1.已知:如图,,垂足为,为过点的一条直线,则与一定成立的关系是( ).
A.互余 B.互补 C.相等 D.不确定
2.如图,已知直线被直线c所截,,,则的度数为( )
A. B. C. D.
3.如图,a∥b,则下列结论中正确的是( )
A.∠1=∠2 B.∠2+∠3=180° C.∠1=∠4 D.∠2=4
4.在下列各图中,与是对顶角的是( )
A. B. C. D.
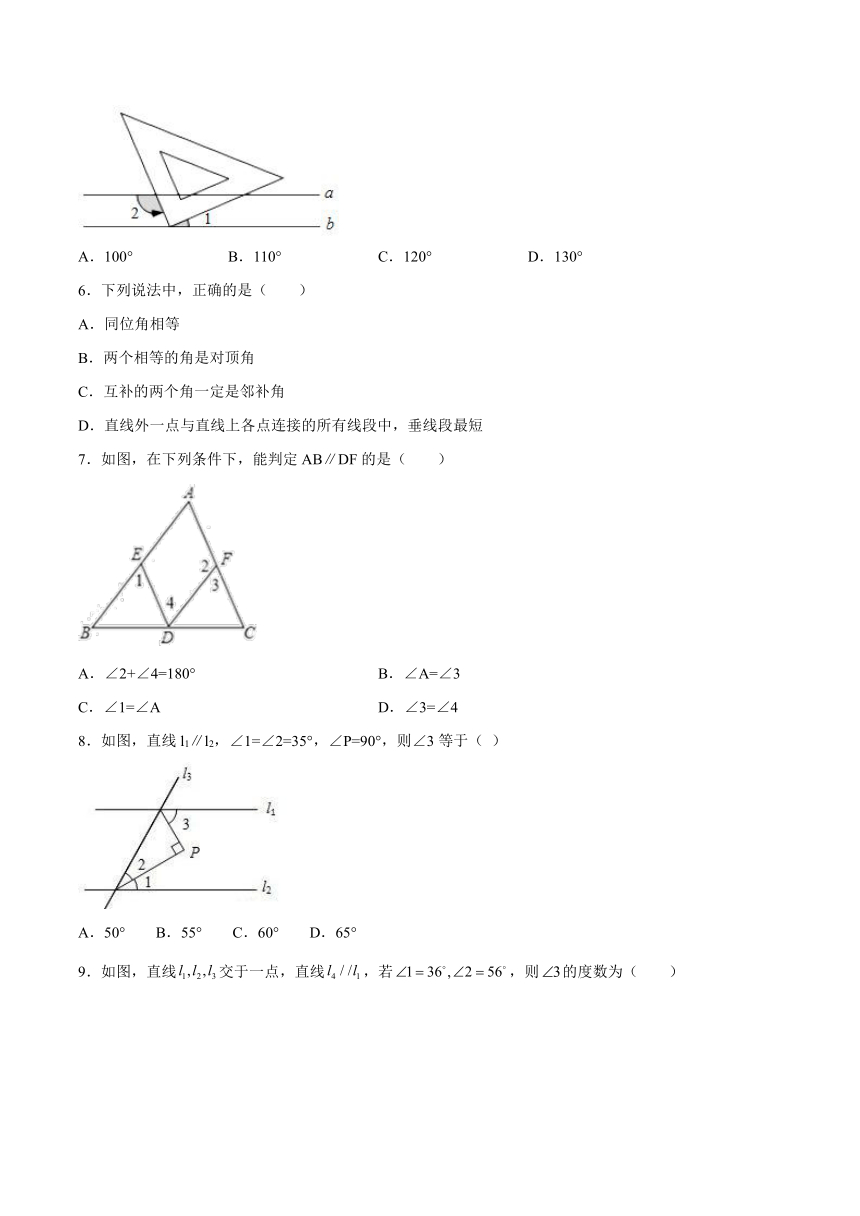
5.如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为( )
A.100° B.110° C.120° D.130°
6.下列说法中,正确的是( )
A.同位角相等
B.两个相等的角是对顶角
C.互补的两个角一定是邻补角
D.直线外一点与直线上各点连接的所有线段中,垂线段最短
7.如图,在下列条件下,能判定AB∥DF的是( )
A.∠2+∠4=180° B.∠A=∠3
C.∠1=∠A D.∠3=∠4
8.如图,直线l1∥l2,∠1=∠2=35°,∠P=90°,则∠3等于( )
A.50° B.55° C.60° D.65°
9.如图,直线交于一点,直线,若,则的度数为( )
A. B. C. D.
10.如图,能推断AD//BC的是( )
A.; B.; C. ; D..
11.下列说法正确的是( )
A.同位角相等 B.相等的角是对顶角
C.垂线段最短 D.两直线平行,同旁内角相等
12.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于( )
A.23° B.16° C.20° D.26°
13.如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A.∠1+∠2 ∠3=90° B.∠1 ∠2+∠3=90° C.∠1+∠2+∠3=90° D.∠2+∠3 ∠1=180°
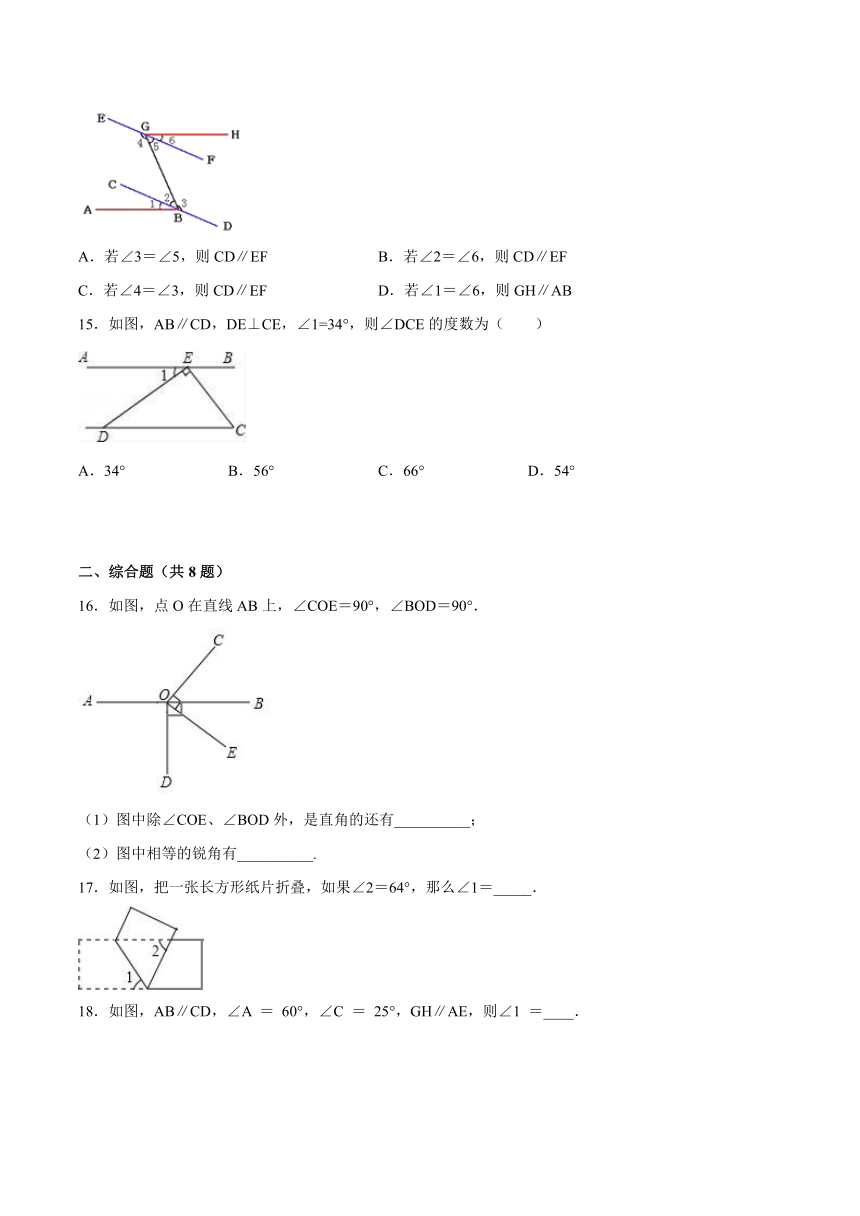
14.如图所示,下列说法正确的是( )
A.若∠3=∠5,则CD∥EF B.若∠2=∠6,则CD∥EF
C.若∠4=∠3,则CD∥EF D.若∠1=∠6,则GH∥AB
15.如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
A.34° B.56° C.66° D.54°
二、综合题(共8题)
16.如图,点O在直线AB上,∠COE=90°,∠BOD=90°.
(1)图中除∠COE、∠BOD外,是直角的还有__________;
(2)图中相等的锐角有__________.
17.如图,把一张长方形纸片折叠,如果∠2=64°,那么∠1=_____.
18.如图,AB∥CD,∠A = 60°,∠C = 25°,GH∥AE,则∠1 =____.
19.如图,已知AB∥CD,∠C=65°,∠E=25°,则∠A的度数为_____.
20.如图,已知∠1=∠2,AB∥EF,∠3=130°,求∠4的度数.
21.如图,平分,点,分别在边,上,且,延长,交于点,求证:.
22.如图,已知AD⊥BC于D,FG⊥BC垂足分别为D,G,且∠1=∠2,∠C=50°,求∠EDC的度数.
证明:∵AD⊥BC,FG⊥BC,
∴∠ADC=∠FGC=90°( ).
∴______//FG( ).
∴∠1=∠3,
又∵∠1=∠2,
∴∠2=∠3( ).
∴DE//______.( ).
∴∠EDC+∠C=180°( ).
∵∠C=50°.
∴∠EDC= °.
23.如图所示:直线AB∥CD,DE∥BC,∠B=(2x+10)°,∠D=(60-3x)°,求x的值及∠BCD的度数.
参考答案
1.A
【详解】
根据图形可看出,∠2的对顶角∠COE与∠1互余,那么∠1与∠2就互余.
解:图中,∠2=∠COE(对顶角相等),
又∵AB⊥CD,
∴∠1+∠COE=90°,
∴∠1+∠2=90°,
∴两角互余.
故选A.
本题考查了余角和垂线的定义以及对顶角相等的性质.
2.B
【详解】
如图,
已知a∥b,∠1=60°,根据平行线的性质可得∠3=∠1=60°,所以∠2=180°﹣∠1=180°-60°=120°,故选B.
3.D
【详解】
∵a∥b,
∴∠4=∠5.
又∵∠2=∠5,
∴∠2=∠4.
故选:D.
4.D
【详解】
解:A、∠1和∠2没有公共的顶点,不是对顶角,选项错误;
B、∠1和∠2没有公共的顶点,不是对顶角,选项错误;
C、不是两条直线相交所成的角,不是对顶角,选项错误;
D、符合对顶角的定义,选项正确;
故选:D.
5.D
【详解】
解:如图,
∵∠1+∠3=90°,
∴∠3=90°﹣40°=50°,
∵a∥b,
∴∠2+∠3=180°.
∴∠2=180°﹣50°=130°.
故选D.
6.D
【详解】
解:A、两直线平行,同位角相等,故本选项错误,不符合题意;
B、对顶角相等,但相等的两个角不一定是对顶角,故本选项错误,不符合题意;
C、邻补角互补,但互补的两个角不一定是邻补角,故本选项错误,不符合题意;
D、直线外一点与直线上各点连接的所有线段中,垂线段最短,故本选项正确,故符合题意.
故选:D.
7.B
【详解】
解:A、∵∠2+∠4=180,∴AF∥ED,不能判定AB∥DF,故选项不符合;
B、∵∠A=∠3,∴AB∥DF,故选项符合;
C、∵∠1=∠A,∴AC∥ED,不能判定AB∥DF,故选项不符合;
D、∵∠3=∠4,∴AC∥ED,不能判定AB∥DF,故选项不符合;
故选:B.
8.B
【解析】
试题分析:先根据两直线平行,同旁内角互补,求出∠3与∠4的和,再根据直角三角形两锐角互余求出∠4,∠3即可求得:
如图,∵l1∥l2,∴∠1+∠2+∠3+∠4=180°.
∵∠1=∠2=35°,∴∠3+∠4=110°.
∵∠P=90°,∠2=35°,∴∠4=90°-35°=55°.
∴∠3=110°-55°=55°.
故选B.
9.A
【详解】
解:如图,
,
,
.
故选:.
10.C
【详解】
A中,由可得出,故该选项错误;
B中,由可得出,故该选项错误;
C中,根据同位角相等,两直线平行可以得出,故该选项正确;
D中,由可得出,故该选项错误;
故选:C.
11.C
【详解】
解:A.同位角不一定相等,只有两直线平行,同位角相等,故A错误;
B.相等的角不一定是对顶角,而对顶角才相等,故B错误;
C.直线外一点与直线上各点的连线中,垂线段最短,故C正确.
D.两直线平行,同旁内角不一定相等,但一定互补,故D错误;
故选C.
12.C
【详解】
分析:根据平行线的性质得到∠BCD=∠ABC=46°,∠FEC+∠ECD=180,求出∠ECD,根据∠BCE=∠BCD-∠ECD求出即可.
解答:解:∵AB∥EF∥CD,∠ABC=46°,∠CEF=154°,
∴∠BCD=∠ABC=46°,∠FEC+∠ECD=180°,
∴∠ECD=180°-∠FEC=26°,
∴∠BCE=∠BCD-∠ECD=46°-26°=20°.
故选C.
13.D
【详解】
∵EF∥CD
∴∠3=∠COE
∴∠3 ∠1=∠COE ∠1=∠BOE
∵AB∥EF
∴∠2+∠BOE=180°,即∠2+∠3 ∠1=180°
故选:D.
14.C
【解析】
解:∠4和∠3是直线EF和CD被直线GB所截形成的内错角,所以∠4=∠3时,CD∥EF.故选C.
15.B
【详解】
试题分析:∵AB∥CD,
∴∠D=∠1=34°,
∵DE⊥CE,
∴∠DEC=90°,
∴∠DCE=180°﹣90°﹣34°=56°.
故选B.
16.∠AOD ∠COB=∠DOE
【详解】
(1)∵ 点O在直线AB上,且∠BOD=90°,
∴ ∠AOD=180°-90°=90°.
(2)∵ ∠COE=90°,∴ ∠COB+∠BOE=∠DOE+∠BOE,∴ ∠COB=∠DOE.
17.58°.
【详解】
解:如右图所示,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠2=∠4,
又∵∠1折叠后与∠3重合,
∴∠1=∠3,
又∵∠1+∠3+∠4=180°,
∴2∠1=180°﹣64°=116°,
∴∠1=58°,
故答案为58°.
18.145°
【解析】
∵
∴
∴
又∵分别是中点
∴
∴
∴
19.40°
【解析】
∵AB∥CD,∠C=65°
∴∠BFE=∠C=65°,
∴A=∠BFE-∠E=65°-25°=40°.
20.∠4=50°
【详解】
解:∵∠1=∠2
∴AB∥CD
∵AB∥EF
∴CD∥EF
∴∠4+∠3=180°
∵∠3=130°
∴∠4+=180°-130°=50°
21.证明见解析.
【详解】
平分,
,
,
,
,
,
又,
,
由对顶角相等得:,
.
22.垂直的定义;AD;同位角相等,两直线平行;等量代换;AC;内错角相等,两直线平行;两直线平行,同旁内角互补;130.
【详解】
证明:,,
,垂直的定义,
同位角相等,两直线平行,
.
又,
等量代换,
内错角相等,两直线平行
两直线平行,同旁内角互补.
.
.
故答案为:垂直的定义;AD;同位角相等,两直线平行;等量代换;AC;内错角相等,两直线平行;两直线平行,同旁内角互补;130.
23.10;30°.
【解析】
试题分析:根据AB∥CD,得∠B=∠1,由DE∥BC,得∠D=∠1,所以∠B=∠D,代入列方程求解即可.
一、选择题(共15题)
1.已知:如图,,垂足为,为过点的一条直线,则与一定成立的关系是( ).
A.互余 B.互补 C.相等 D.不确定
2.如图,已知直线被直线c所截,,,则的度数为( )
A. B. C. D.
3.如图,a∥b,则下列结论中正确的是( )
A.∠1=∠2 B.∠2+∠3=180° C.∠1=∠4 D.∠2=4
4.在下列各图中,与是对顶角的是( )
A. B. C. D.
5.如图,已知a∥b,小华把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为( )
A.100° B.110° C.120° D.130°
6.下列说法中,正确的是( )
A.同位角相等
B.两个相等的角是对顶角
C.互补的两个角一定是邻补角
D.直线外一点与直线上各点连接的所有线段中,垂线段最短
7.如图,在下列条件下,能判定AB∥DF的是( )
A.∠2+∠4=180° B.∠A=∠3
C.∠1=∠A D.∠3=∠4
8.如图,直线l1∥l2,∠1=∠2=35°,∠P=90°,则∠3等于( )
A.50° B.55° C.60° D.65°
9.如图,直线交于一点,直线,若,则的度数为( )
A. B. C. D.
10.如图,能推断AD//BC的是( )
A.; B.; C. ; D..
11.下列说法正确的是( )
A.同位角相等 B.相等的角是对顶角
C.垂线段最短 D.两直线平行,同旁内角相等
12.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于( )
A.23° B.16° C.20° D.26°
13.如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A.∠1+∠2 ∠3=90° B.∠1 ∠2+∠3=90° C.∠1+∠2+∠3=90° D.∠2+∠3 ∠1=180°
14.如图所示,下列说法正确的是( )
A.若∠3=∠5,则CD∥EF B.若∠2=∠6,则CD∥EF
C.若∠4=∠3,则CD∥EF D.若∠1=∠6,则GH∥AB
15.如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
A.34° B.56° C.66° D.54°
二、综合题(共8题)
16.如图,点O在直线AB上,∠COE=90°,∠BOD=90°.
(1)图中除∠COE、∠BOD外,是直角的还有__________;
(2)图中相等的锐角有__________.
17.如图,把一张长方形纸片折叠,如果∠2=64°,那么∠1=_____.
18.如图,AB∥CD,∠A = 60°,∠C = 25°,GH∥AE,则∠1 =____.
19.如图,已知AB∥CD,∠C=65°,∠E=25°,则∠A的度数为_____.
20.如图,已知∠1=∠2,AB∥EF,∠3=130°,求∠4的度数.
21.如图,平分,点,分别在边,上,且,延长,交于点,求证:.
22.如图,已知AD⊥BC于D,FG⊥BC垂足分别为D,G,且∠1=∠2,∠C=50°,求∠EDC的度数.
证明:∵AD⊥BC,FG⊥BC,
∴∠ADC=∠FGC=90°( ).
∴______//FG( ).
∴∠1=∠3,
又∵∠1=∠2,
∴∠2=∠3( ).
∴DE//______.( ).
∴∠EDC+∠C=180°( ).
∵∠C=50°.
∴∠EDC= °.
23.如图所示:直线AB∥CD,DE∥BC,∠B=(2x+10)°,∠D=(60-3x)°,求x的值及∠BCD的度数.
参考答案
1.A
【详解】
根据图形可看出,∠2的对顶角∠COE与∠1互余,那么∠1与∠2就互余.
解:图中,∠2=∠COE(对顶角相等),
又∵AB⊥CD,
∴∠1+∠COE=90°,
∴∠1+∠2=90°,
∴两角互余.
故选A.
本题考查了余角和垂线的定义以及对顶角相等的性质.
2.B
【详解】
如图,
已知a∥b,∠1=60°,根据平行线的性质可得∠3=∠1=60°,所以∠2=180°﹣∠1=180°-60°=120°,故选B.
3.D
【详解】
∵a∥b,
∴∠4=∠5.
又∵∠2=∠5,
∴∠2=∠4.
故选:D.
4.D
【详解】
解:A、∠1和∠2没有公共的顶点,不是对顶角,选项错误;
B、∠1和∠2没有公共的顶点,不是对顶角,选项错误;
C、不是两条直线相交所成的角,不是对顶角,选项错误;
D、符合对顶角的定义,选项正确;
故选:D.
5.D
【详解】
解:如图,
∵∠1+∠3=90°,
∴∠3=90°﹣40°=50°,
∵a∥b,
∴∠2+∠3=180°.
∴∠2=180°﹣50°=130°.
故选D.
6.D
【详解】
解:A、两直线平行,同位角相等,故本选项错误,不符合题意;
B、对顶角相等,但相等的两个角不一定是对顶角,故本选项错误,不符合题意;
C、邻补角互补,但互补的两个角不一定是邻补角,故本选项错误,不符合题意;
D、直线外一点与直线上各点连接的所有线段中,垂线段最短,故本选项正确,故符合题意.
故选:D.
7.B
【详解】
解:A、∵∠2+∠4=180,∴AF∥ED,不能判定AB∥DF,故选项不符合;
B、∵∠A=∠3,∴AB∥DF,故选项符合;
C、∵∠1=∠A,∴AC∥ED,不能判定AB∥DF,故选项不符合;
D、∵∠3=∠4,∴AC∥ED,不能判定AB∥DF,故选项不符合;
故选:B.
8.B
【解析】
试题分析:先根据两直线平行,同旁内角互补,求出∠3与∠4的和,再根据直角三角形两锐角互余求出∠4,∠3即可求得:
如图,∵l1∥l2,∴∠1+∠2+∠3+∠4=180°.
∵∠1=∠2=35°,∴∠3+∠4=110°.
∵∠P=90°,∠2=35°,∴∠4=90°-35°=55°.
∴∠3=110°-55°=55°.
故选B.
9.A
【详解】
解:如图,
,
,
.
故选:.
10.C
【详解】
A中,由可得出,故该选项错误;
B中,由可得出,故该选项错误;
C中,根据同位角相等,两直线平行可以得出,故该选项正确;
D中,由可得出,故该选项错误;
故选:C.
11.C
【详解】
解:A.同位角不一定相等,只有两直线平行,同位角相等,故A错误;
B.相等的角不一定是对顶角,而对顶角才相等,故B错误;
C.直线外一点与直线上各点的连线中,垂线段最短,故C正确.
D.两直线平行,同旁内角不一定相等,但一定互补,故D错误;
故选C.
12.C
【详解】
分析:根据平行线的性质得到∠BCD=∠ABC=46°,∠FEC+∠ECD=180,求出∠ECD,根据∠BCE=∠BCD-∠ECD求出即可.
解答:解:∵AB∥EF∥CD,∠ABC=46°,∠CEF=154°,
∴∠BCD=∠ABC=46°,∠FEC+∠ECD=180°,
∴∠ECD=180°-∠FEC=26°,
∴∠BCE=∠BCD-∠ECD=46°-26°=20°.
故选C.
13.D
【详解】
∵EF∥CD
∴∠3=∠COE
∴∠3 ∠1=∠COE ∠1=∠BOE
∵AB∥EF
∴∠2+∠BOE=180°,即∠2+∠3 ∠1=180°
故选:D.
14.C
【解析】
解:∠4和∠3是直线EF和CD被直线GB所截形成的内错角,所以∠4=∠3时,CD∥EF.故选C.
15.B
【详解】
试题分析:∵AB∥CD,
∴∠D=∠1=34°,
∵DE⊥CE,
∴∠DEC=90°,
∴∠DCE=180°﹣90°﹣34°=56°.
故选B.
16.∠AOD ∠COB=∠DOE
【详解】
(1)∵ 点O在直线AB上,且∠BOD=90°,
∴ ∠AOD=180°-90°=90°.
(2)∵ ∠COE=90°,∴ ∠COB+∠BOE=∠DOE+∠BOE,∴ ∠COB=∠DOE.
17.58°.
【详解】
解:如右图所示,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠2=∠4,
又∵∠1折叠后与∠3重合,
∴∠1=∠3,
又∵∠1+∠3+∠4=180°,
∴2∠1=180°﹣64°=116°,
∴∠1=58°,
故答案为58°.
18.145°
【解析】
∵
∴
∴
又∵分别是中点
∴
∴
∴
19.40°
【解析】
∵AB∥CD,∠C=65°
∴∠BFE=∠C=65°,
∴A=∠BFE-∠E=65°-25°=40°.
20.∠4=50°
【详解】
解:∵∠1=∠2
∴AB∥CD
∵AB∥EF
∴CD∥EF
∴∠4+∠3=180°
∵∠3=130°
∴∠4+=180°-130°=50°
21.证明见解析.
【详解】
平分,
,
,
,
,
,
又,
,
由对顶角相等得:,
.
22.垂直的定义;AD;同位角相等,两直线平行;等量代换;AC;内错角相等,两直线平行;两直线平行,同旁内角互补;130.
【详解】
证明:,,
,垂直的定义,
同位角相等,两直线平行,
.
又,
等量代换,
内错角相等,两直线平行
两直线平行,同旁内角互补.
.
.
故答案为:垂直的定义;AD;同位角相等,两直线平行;等量代换;AC;内错角相等,两直线平行;两直线平行,同旁内角互补;130.
23.10;30°.
【解析】
试题分析:根据AB∥CD,得∠B=∠1,由DE∥BC,得∠D=∠1,所以∠B=∠D,代入列方程求解即可.
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
