八年级数学10.1平方根(3)
文档属性
| 名称 | 八年级数学10.1平方根(3) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-24 00:00:00 | ||
图片预览






文档简介
课件19张PPT。 在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
-------毕达哥拉斯 思考±0.8±3±4±1±6 0平方等于一个正数的数有 个,它们 。
平方等于0的数有 个,是 ;
平方等于一个负数的数 。
归纳:互为相反数两一0不存在 不存在(3)填一填(2)平方等于0.64的数有几个?(1)平方等于9的数是 .13.1平方根(3)
探究新知±4±1±60一般地,如果一个数X的平方等于a,即 X2 = a,
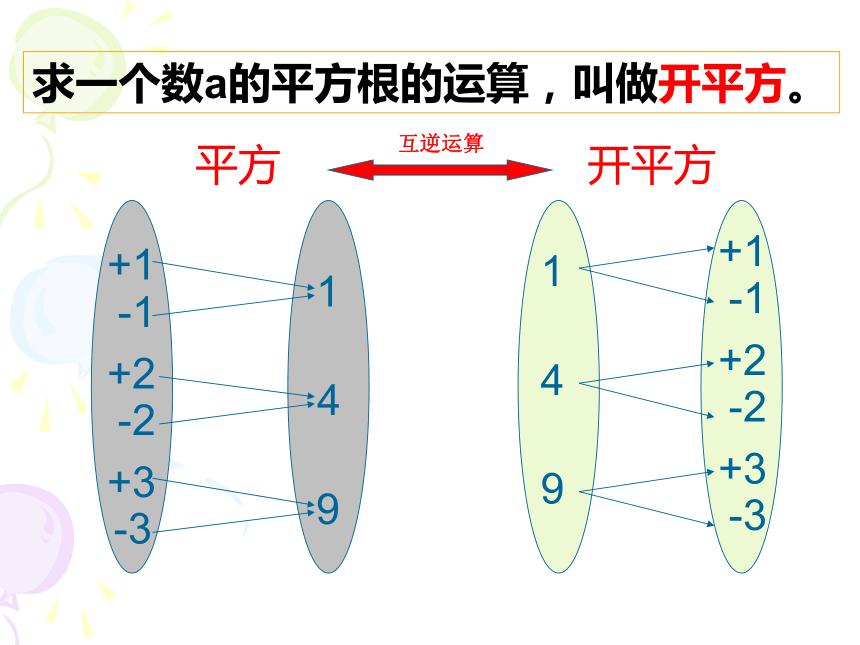
那么这个数X叫做a的平方根(或二次方根).不存在求一个数a的平方根的运算,叫做开平方。刚才填表的过程实际是已知 ,求 的运算过程。思考:一个数aa的平方根求一个数a的平方根的运算,叫做开平方。149+1-1+2-2+3-3149+1-1+2-2+3-3开平方平方互逆运算 例 1、用平方根的定义求下列各数的平方根.1) 100 2) 3) 0.25解:1) ∵ ( 10 )2 =100, ∴ 100的平方根是 10. 2) ∵ ( )2= , ∴ 的平方根是 .3) ∵ ( 0.5)2 = 0.25,∴ 0.25 的平方根是 0.5.4)05)-4你能发现一个数的平方根有哪些性质吗?思考:4)∵ 02=0
∴0的平方根是05) ∵任何一个数的平方 都不为负数
∴-4没有平方根两个互为相反数0没有平方根0的平方根是 ;负数 。关于平方根的性质:正数有 个平方根,它们 ;5有平方根吗?你能表示吗?如果一个数X的平方等于a,即 X2 = a,
那么这个数X叫做a的平方根(二次方根)a的平方根表示为符号表示5的平方根表示为你能比较非负数a的算术平方根和平方根吗?你一言我一语归纳整理对于非负数a:概念符号
表示如果一个正数x的平方等于a,那么这个正数x叫做a的算术平方根.如果一个数X的平方等于a,那么这个数X叫做a的平方根(或二次方根)性质非负数a的正的平方根就是它的算术平方根。正数有一个算术平方根;0的算术平方根是0;负数没有算术平方根。正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根。例2 下列式子表示什么意义?你能求出它 们的值吗?
(l)± (2) -
(3) (4)
4) 的平方根是 ± 4 。 ( )1) 1.21 的平方根是 ± 1.1 。 ( )2) -5是25的平方根 。 ( ) 3) 25 的平方根是- 5 。 ( )√××√测试你的判断力:6) 0的算术平方根是它的平方根. ( )7) -6是(-6)2的一个平方根. ( ) 8) 如果两个数平方后相等,那么它们也 相等. ( )√×√5) 平方根是本身的数有0 ,1 . ( ) ×(2)(x-1)2=4例3你能求出下列各式中未知数x的值吗?(1) x2=169(3)3(x-1)2 - 39=0平方根概念的起源与几何中的正方形有关,如果一个正方形的面积为A,那么这个正方形的边长是多少?例4、2) 3a-22和2a-3是m的平方根,
试求m的值。拓广探索1) m的两个平方根是3a-22和2a-3,
试求m的值。3) :平方根的概念、表示方法、求法及平方根的性质。
:平方运算和开平方运算互为逆运算,可以互相检验。
:类比学习。
:由特殊到一般,再由一般到特殊,是发现问题和解决问题的基本方法和途径本节课你有什么收获?1、数学知识2、数学思维3、数学方法4、探究策略go作业作业本(1)P16谢谢大家!再见
-------毕达哥拉斯 思考±0.8±3±4±1±6 0平方等于一个正数的数有 个,它们 。
平方等于0的数有 个,是 ;
平方等于一个负数的数 。
归纳:互为相反数两一0不存在 不存在(3)填一填(2)平方等于0.64的数有几个?(1)平方等于9的数是 .13.1平方根(3)
探究新知±4±1±60一般地,如果一个数X的平方等于a,即 X2 = a,
那么这个数X叫做a的平方根(或二次方根).不存在求一个数a的平方根的运算,叫做开平方。刚才填表的过程实际是已知 ,求 的运算过程。思考:一个数aa的平方根求一个数a的平方根的运算,叫做开平方。149+1-1+2-2+3-3149+1-1+2-2+3-3开平方平方互逆运算 例 1、用平方根的定义求下列各数的平方根.1) 100 2) 3) 0.25解:1) ∵ ( 10 )2 =100, ∴ 100的平方根是 10. 2) ∵ ( )2= , ∴ 的平方根是 .3) ∵ ( 0.5)2 = 0.25,∴ 0.25 的平方根是 0.5.4)05)-4你能发现一个数的平方根有哪些性质吗?思考:4)∵ 02=0
∴0的平方根是05) ∵任何一个数的平方 都不为负数
∴-4没有平方根两个互为相反数0没有平方根0的平方根是 ;负数 。关于平方根的性质:正数有 个平方根,它们 ;5有平方根吗?你能表示吗?如果一个数X的平方等于a,即 X2 = a,
那么这个数X叫做a的平方根(二次方根)a的平方根表示为符号表示5的平方根表示为你能比较非负数a的算术平方根和平方根吗?你一言我一语归纳整理对于非负数a:概念符号
表示如果一个正数x的平方等于a,那么这个正数x叫做a的算术平方根.如果一个数X的平方等于a,那么这个数X叫做a的平方根(或二次方根)性质非负数a的正的平方根就是它的算术平方根。正数有一个算术平方根;0的算术平方根是0;负数没有算术平方根。正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根。例2 下列式子表示什么意义?你能求出它 们的值吗?
(l)± (2) -
(3) (4)
4) 的平方根是 ± 4 。 ( )1) 1.21 的平方根是 ± 1.1 。 ( )2) -5是25的平方根 。 ( ) 3) 25 的平方根是- 5 。 ( )√××√测试你的判断力:6) 0的算术平方根是它的平方根. ( )7) -6是(-6)2的一个平方根. ( ) 8) 如果两个数平方后相等,那么它们也 相等. ( )√×√5) 平方根是本身的数有0 ,1 . ( ) ×(2)(x-1)2=4例3你能求出下列各式中未知数x的值吗?(1) x2=169(3)3(x-1)2 - 39=0平方根概念的起源与几何中的正方形有关,如果一个正方形的面积为A,那么这个正方形的边长是多少?例4、2) 3a-22和2a-3是m的平方根,
试求m的值。拓广探索1) m的两个平方根是3a-22和2a-3,
试求m的值。3) :平方根的概念、表示方法、求法及平方根的性质。
:平方运算和开平方运算互为逆运算,可以互相检验。
:类比学习。
:由特殊到一般,再由一般到特殊,是发现问题和解决问题的基本方法和途径本节课你有什么收获?1、数学知识2、数学思维3、数学方法4、探究策略go作业作业本(1)P16谢谢大家!再见
