华东师大版数学七年级上册 2.11 有理数的乘方(3) 课件(共13张ppt)
文档属性
| 名称 | 华东师大版数学七年级上册 2.11 有理数的乘方(3) 课件(共13张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 161.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 21:24:43 | ||
图片预览




文档简介
(共13张PPT)
2.11 有理数的乘方
教学目标 :
1.理解有理数乘方的意义,正确理解乘方、幂、指数、底数等概念,会进行有理数乘方的运算。
2.通过对乘方意义的理解,培养学生观察、比较、分析、归纳、概括的能力,渗透转化的数学思想。
教学重点:
正确理解乘方的意义,弄清底数、指数、幂等概念,掌握乘方运算法则。
教学难点:
正确理解各种概念并合理运算。
问题情景1
活动要求:两人合作把一张纸进行对折、再对折……并作记录
问题:(1)对折一次有几层?
(2)对折二次有几层?
(3)对折三次有几层?
(4)对折四次有几层?
(5)对折五次有几层?
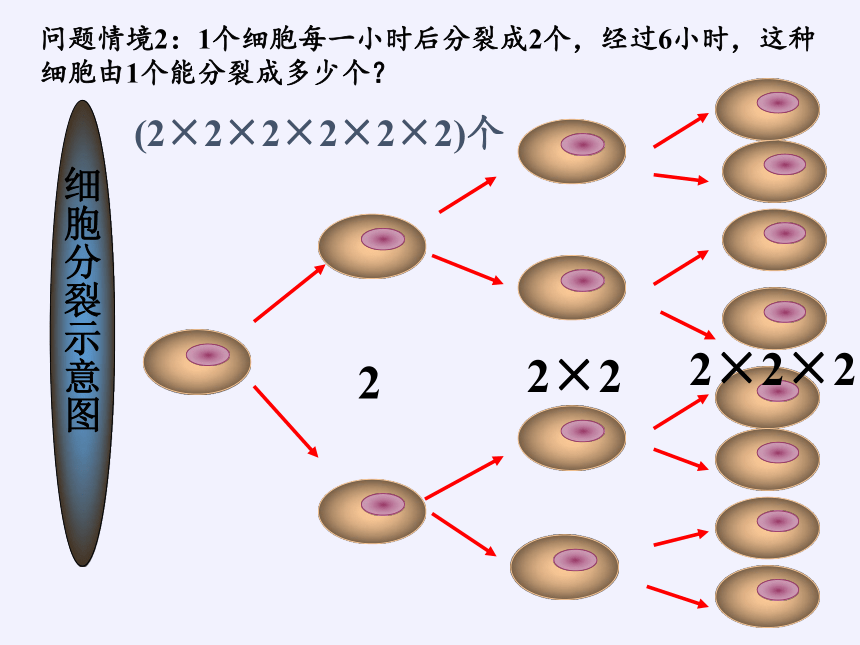
细胞分裂示意图
2
2×2
2×2×2
问题情境2:1个细胞每一小时后分裂成2个,经过6小时,这种细胞由1个能分裂成多少个?
(2×2×2×2×2×2)个
请比较折纸六次后纸的层数2×2×2×2×2
和细胞分裂六次后的个数式子: 2×2×2×2×2×2.
它们有什么相同点
答:它们都是乘法;并且它们各自的因数都相同.
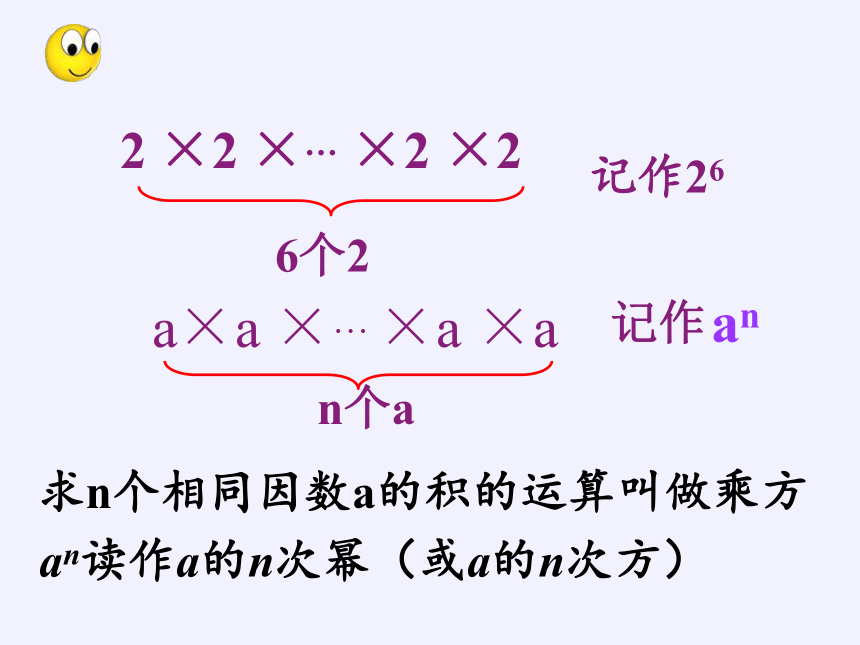
2 ×2 ×… ×2 ×2
6个2
求n个相同因数a的积的运算叫做乘方
an读作a的n次幂(或a的n次方)
记作26
记作
an
a×a ×… ×a ×a
n个a
an
底数
指数
幂
(1) 53
(2)(-3)4
(3)
练习:说出下列各式的底数、指数、及其读法
注意:当底数是负数或分数时,底数一定
要加上括弧,这也是辩认底数的方法.
1
2
( ) 3
如:
、(-3)2
(1) (-2)3 (2) (-2)4 (3) (-2)5
(1) (-2)3
解:
(2) (-2)4
(3) (-2)5
= -8
=16
-32
例1:计算:
=
=(-2)×(-2)×(-2)
=(-2)×(-2)×(-2)×(-2)
=(-2)×(-2)×(-2)×(-2)×(-2)
例2 计算(1)5 3 ,(2)(- 4)4 , (3) (- ) 3
解: (1)53=5×5×5=125 (2)(-4)4=(-4) ×(-4) ×(-4) ×(-4)=256
(3)(- )3=(- ) ×(- ) ×(- ) = -
观察例1、2的结果,你能
发现乘方运算的符号有
什么规律?
想一想:
乘方运算的符号规律
正数的任何次幂都是正数
负数的偶次幂是正数,奇
次幂是负数。
课堂小结
1、通过这节课的学习,你有哪些收获
2、乘方的结果叫做幂
a×a ×… ×a ×a
n个a
an=
作业 P58 1 2 4
谢 谢
2.11 有理数的乘方
教学目标 :
1.理解有理数乘方的意义,正确理解乘方、幂、指数、底数等概念,会进行有理数乘方的运算。
2.通过对乘方意义的理解,培养学生观察、比较、分析、归纳、概括的能力,渗透转化的数学思想。
教学重点:
正确理解乘方的意义,弄清底数、指数、幂等概念,掌握乘方运算法则。
教学难点:
正确理解各种概念并合理运算。
问题情景1
活动要求:两人合作把一张纸进行对折、再对折……并作记录
问题:(1)对折一次有几层?
(2)对折二次有几层?
(3)对折三次有几层?
(4)对折四次有几层?
(5)对折五次有几层?
细胞分裂示意图
2
2×2
2×2×2
问题情境2:1个细胞每一小时后分裂成2个,经过6小时,这种细胞由1个能分裂成多少个?
(2×2×2×2×2×2)个
请比较折纸六次后纸的层数2×2×2×2×2
和细胞分裂六次后的个数式子: 2×2×2×2×2×2.
它们有什么相同点
答:它们都是乘法;并且它们各自的因数都相同.
2 ×2 ×… ×2 ×2
6个2
求n个相同因数a的积的运算叫做乘方
an读作a的n次幂(或a的n次方)
记作26
记作
an
a×a ×… ×a ×a
n个a
an
底数
指数
幂
(1) 53
(2)(-3)4
(3)
练习:说出下列各式的底数、指数、及其读法
注意:当底数是负数或分数时,底数一定
要加上括弧,这也是辩认底数的方法.
1
2
( ) 3
如:
、(-3)2
(1) (-2)3 (2) (-2)4 (3) (-2)5
(1) (-2)3
解:
(2) (-2)4
(3) (-2)5
= -8
=16
-32
例1:计算:
=
=(-2)×(-2)×(-2)
=(-2)×(-2)×(-2)×(-2)
=(-2)×(-2)×(-2)×(-2)×(-2)
例2 计算(1)5 3 ,(2)(- 4)4 , (3) (- ) 3
解: (1)53=5×5×5=125 (2)(-4)4=(-4) ×(-4) ×(-4) ×(-4)=256
(3)(- )3=(- ) ×(- ) ×(- ) = -
观察例1、2的结果,你能
发现乘方运算的符号有
什么规律?
想一想:
乘方运算的符号规律
正数的任何次幂都是正数
负数的偶次幂是正数,奇
次幂是负数。
课堂小结
1、通过这节课的学习,你有哪些收获
2、乘方的结果叫做幂
a×a ×… ×a ×a
n个a
an=
作业 P58 1 2 4
谢 谢
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
