25.3._用频率估计概率
图片预览






文档简介
课件24张PPT。用频率估计概率(1) 第二十五章 概率初步复习1.试验的所有可能结果只有______个;2.每一个试验结果出现的可能性____.一、等可能性事件 如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率二、求等可能性事件概率的方法:有限相等归纳列举法求事件的概率(1)事件结果显而易见,可能性较少,可用________(2)涉及两个因素,可能出现的结果较多,可用_______或_______(3)涉及三个或以上的因素,事件结果较复杂,步骤较多,可用________(4)对于不可放回事件的概率,用____________较方便.直接列举法列表法画树形图法画树形图法画树形图法复习1、有三枚硬币,硬币1的一面涂有红
色,另一面涂有黄色;硬币2的一面涂
有黄色,另一面涂有蓝色;硬币3的一
面涂有蓝色,另一面涂有红色。现将
这三枚硬币随意抛出,求两枚的颜色
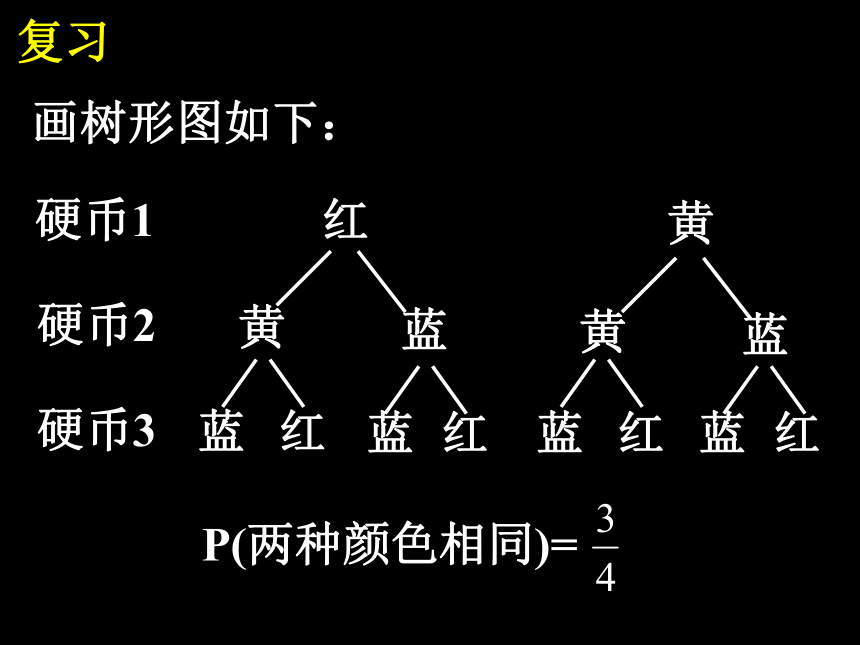
相同的概率。用什么方法求概率?复习画树形图如下:硬币1硬币2硬币3红黄黄蓝黄蓝蓝红蓝红蓝红蓝红P(两种颜色相同)=导入※、如图,有一枚图钉,将它抛出后,
要考察钉尖的朝向上的概率。(1)钉尖的朝向有几种可能的结果?钉尖朝上钉尖朝上(2)这两种结果可能性相等吗?这两种结果可能性不相等。导入※、某林业部门要考察某种幼树在一
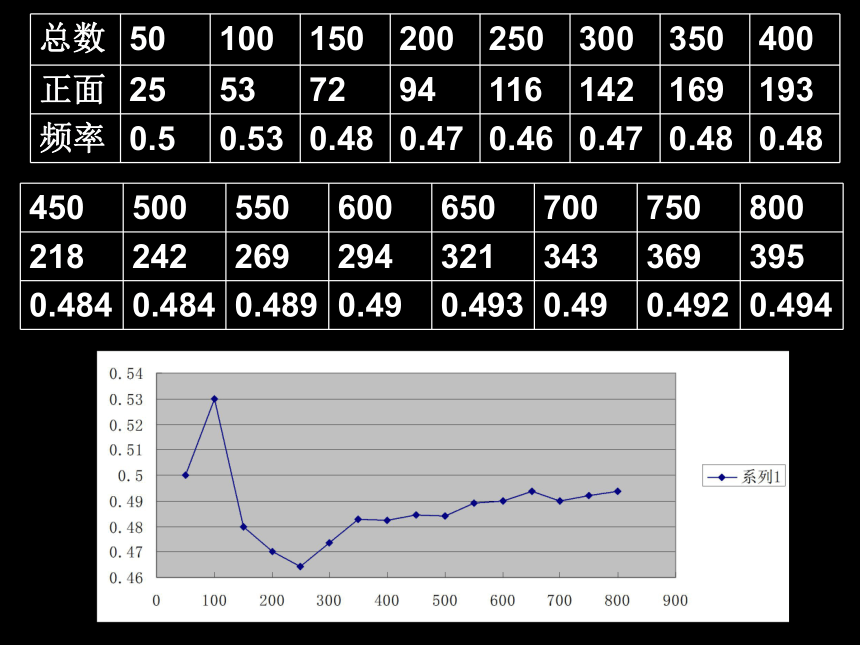
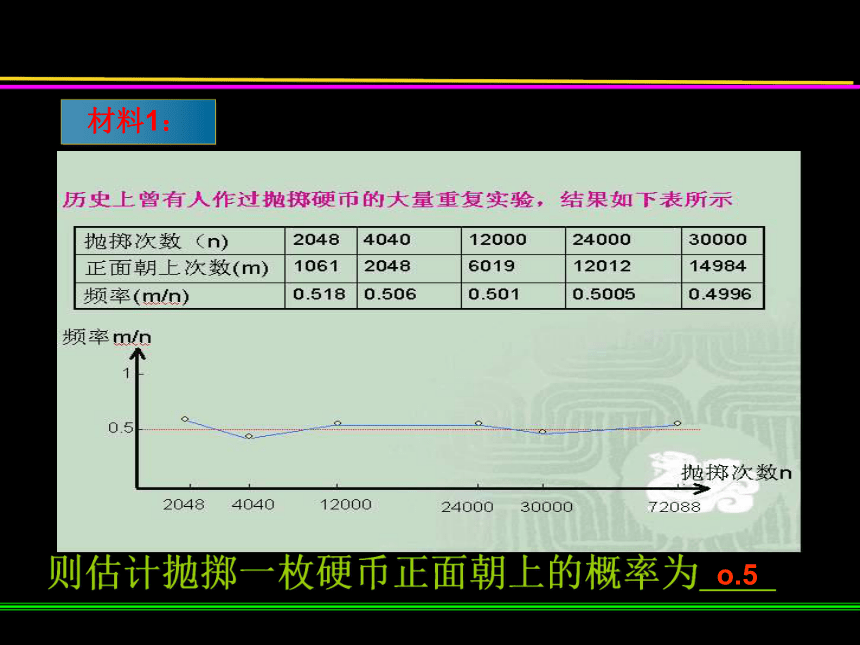
定条件的移植成活的概率。(1)可能的结果有多少种?可能的结果有两种。(2)这两种结果可能性相等吗?这两种结果可能性不相等。材料1:则估计抛掷一枚硬币正面朝上的概率为__o.5探究★、小明做了一个抛图钉试验,有关数据如下:(1)请将表格填写完整;0.5380.5690.5630.5440.5430.5440.5570.5550.5440.543巩固(2)估计图钉钉尖朝上的概率。0.5380.5690.5630.5440.5430.5440.5570.5550.5440.543图钉钉尖朝上的频率稳定在哪个值附近?归纳用频率估计概率的意义: 一般地,在大量重复试验中,如果事件A发生的频率 会稳定在某个常数p附近,那么事件A发生的概率P(A)=p用频率估计概率的条件:(1)试验的所有可能结果不是有限个;(2)试验的各种可能结果发生的可能性不相等.巩固2、在做种子发芽实验时,10000粒种子
有9801粒发芽,据此估计该种子发芽的
概率约为 。范例例1、某林业部门要考察某种幼树在一
定条件的移植成活的概率,应采用什
么具体做法?用频率估计概率范例例1、下表是一张模拟的统计表,请补
充表中的空缺,并完成表后的填空:0.940.92250.8830.9050.897范例0.940.92250.8830.9050.897 成活的频率在 左右摆动,并且随
着统计数据的增加,这种规律愈加明显,
所以估计成活的概率为 。巩固3、从一副没有大小王的52张扑克牌中
随意抽取一张,然后放回洗匀,在抽牌
的试验中得到部分数据:(1)从表上可以发现:随着试验次数的增
加,出现红桃的频率约是多少?
(2)你知道抽取一张红桃的概率是多少?巩固4、水果公司以2元/千克的成本新进了
10000千克柑橘,如果公司希望这些柑
橘能够获得利润5000元,那么在出售
柑橘(已去掉损坏的柑橘)时,每千克大
约定价为多少元比较合适?
销售人员首先从所以的柑橘中随机
抽取若干柑橘,进行了“柑橘损坏率”统
计,并把获得的数据记录在下表中,请
帮忙完成此表。巩固0.1010.0970.0970.0980.0990.1030.1010.103 损坏频率在 左右摆动,所以估计
损坏的概率为 。巩固4、水果公司以2元/千克的成本新进了
10000千克柑橘,如果公司希望这些柑
橘能够获得利润5000元,那么在出售
柑橘(已去掉损坏的柑橘)时,每千克大
约定价为多少元比较合适?范例例2、为了探究啤酒瓶盖抛起后落地时
“正面朝上”的概率,于是有了下面3位
同学的说法及做法。
甲说:我只做了15次试验,就求出了
瓶盖正面朝上的概率;
乙说:我做了50次试验后,不小心将
瓶盖弄丢了,于是我用了一只可乐瓶
盖代替继续试验,直到结束;
丙说:我觉得用一个瓶盖抛,实验速
度太慢,于是找了8个相同型号的啤
酒瓶盖同时抛,直到结束。范例甲说:我只做了15次试验,就求出了瓶
盖正面朝上的概率;
乙说:我做了50次试验后,不小心将瓶
盖弄丢了,于是我用了一只可乐瓶盖代
替继续试验,直到结束;
丙说:我觉得用一个瓶盖抛,实验速度
太慢,于是找了8个相同型号的啤酒瓶
盖同时抛,直到结束。 你认为这三位同学的说法及做法
如何?巩固5、当试验的所有可能结果不是有限个,
或各种可能结果发生的可能性不相等
时,应该( )
A. 通过统计频率估计概率
B. 用列举法求概率
C. 用列表法求概率
D. 用树形图法求概率小结1.用频率估计概率的意义重要思想2.用频率估计概率的条件无限性和非等可能性3.从频率变化观察概率值的方法稳定性和趋势性
色,另一面涂有黄色;硬币2的一面涂
有黄色,另一面涂有蓝色;硬币3的一
面涂有蓝色,另一面涂有红色。现将
这三枚硬币随意抛出,求两枚的颜色
相同的概率。用什么方法求概率?复习画树形图如下:硬币1硬币2硬币3红黄黄蓝黄蓝蓝红蓝红蓝红蓝红P(两种颜色相同)=导入※、如图,有一枚图钉,将它抛出后,
要考察钉尖的朝向上的概率。(1)钉尖的朝向有几种可能的结果?钉尖朝上钉尖朝上(2)这两种结果可能性相等吗?这两种结果可能性不相等。导入※、某林业部门要考察某种幼树在一
定条件的移植成活的概率。(1)可能的结果有多少种?可能的结果有两种。(2)这两种结果可能性相等吗?这两种结果可能性不相等。材料1:则估计抛掷一枚硬币正面朝上的概率为__o.5探究★、小明做了一个抛图钉试验,有关数据如下:(1)请将表格填写完整;0.5380.5690.5630.5440.5430.5440.5570.5550.5440.543巩固(2)估计图钉钉尖朝上的概率。0.5380.5690.5630.5440.5430.5440.5570.5550.5440.543图钉钉尖朝上的频率稳定在哪个值附近?归纳用频率估计概率的意义: 一般地,在大量重复试验中,如果事件A发生的频率 会稳定在某个常数p附近,那么事件A发生的概率P(A)=p用频率估计概率的条件:(1)试验的所有可能结果不是有限个;(2)试验的各种可能结果发生的可能性不相等.巩固2、在做种子发芽实验时,10000粒种子
有9801粒发芽,据此估计该种子发芽的
概率约为 。范例例1、某林业部门要考察某种幼树在一
定条件的移植成活的概率,应采用什
么具体做法?用频率估计概率范例例1、下表是一张模拟的统计表,请补
充表中的空缺,并完成表后的填空:0.940.92250.8830.9050.897范例0.940.92250.8830.9050.897 成活的频率在 左右摆动,并且随
着统计数据的增加,这种规律愈加明显,
所以估计成活的概率为 。巩固3、从一副没有大小王的52张扑克牌中
随意抽取一张,然后放回洗匀,在抽牌
的试验中得到部分数据:(1)从表上可以发现:随着试验次数的增
加,出现红桃的频率约是多少?
(2)你知道抽取一张红桃的概率是多少?巩固4、水果公司以2元/千克的成本新进了
10000千克柑橘,如果公司希望这些柑
橘能够获得利润5000元,那么在出售
柑橘(已去掉损坏的柑橘)时,每千克大
约定价为多少元比较合适?
销售人员首先从所以的柑橘中随机
抽取若干柑橘,进行了“柑橘损坏率”统
计,并把获得的数据记录在下表中,请
帮忙完成此表。巩固0.1010.0970.0970.0980.0990.1030.1010.103 损坏频率在 左右摆动,所以估计
损坏的概率为 。巩固4、水果公司以2元/千克的成本新进了
10000千克柑橘,如果公司希望这些柑
橘能够获得利润5000元,那么在出售
柑橘(已去掉损坏的柑橘)时,每千克大
约定价为多少元比较合适?范例例2、为了探究啤酒瓶盖抛起后落地时
“正面朝上”的概率,于是有了下面3位
同学的说法及做法。
甲说:我只做了15次试验,就求出了
瓶盖正面朝上的概率;
乙说:我做了50次试验后,不小心将
瓶盖弄丢了,于是我用了一只可乐瓶
盖代替继续试验,直到结束;
丙说:我觉得用一个瓶盖抛,实验速
度太慢,于是找了8个相同型号的啤
酒瓶盖同时抛,直到结束。范例甲说:我只做了15次试验,就求出了瓶
盖正面朝上的概率;
乙说:我做了50次试验后,不小心将瓶
盖弄丢了,于是我用了一只可乐瓶盖代
替继续试验,直到结束;
丙说:我觉得用一个瓶盖抛,实验速度
太慢,于是找了8个相同型号的啤酒瓶
盖同时抛,直到结束。 你认为这三位同学的说法及做法
如何?巩固5、当试验的所有可能结果不是有限个,
或各种可能结果发生的可能性不相等
时,应该( )
A. 通过统计频率估计概率
B. 用列举法求概率
C. 用列表法求概率
D. 用树形图法求概率小结1.用频率估计概率的意义重要思想2.用频率估计概率的条件无限性和非等可能性3.从频率变化观察概率值的方法稳定性和趋势性
同课章节目录
