北师大版高中数学必修1《函数的表示法》教学课件(共26张PPT)
文档属性
| 名称 | 北师大版高中数学必修1《函数的表示法》教学课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 21:56:18 | ||
图片预览







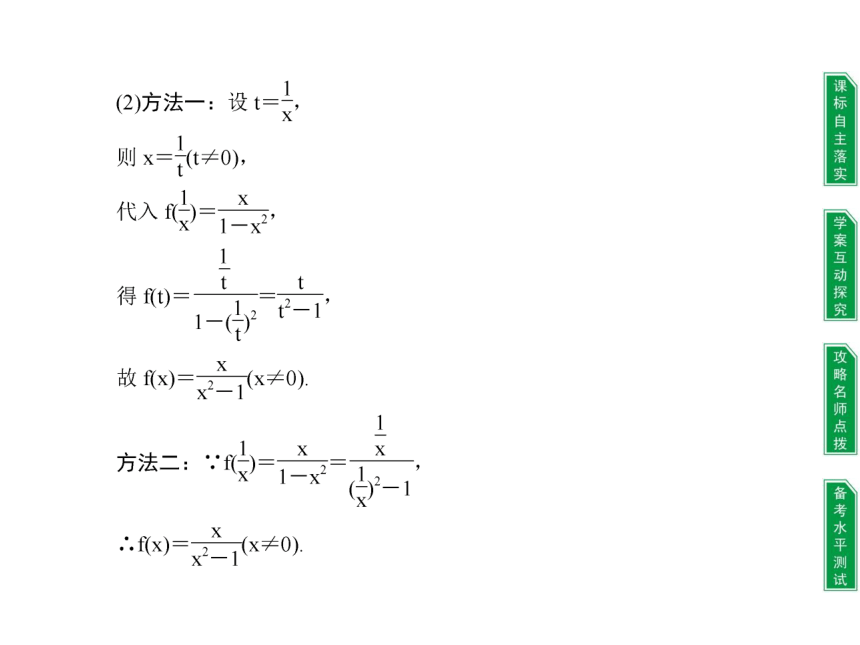
文档简介
(共26张PPT)
2.2 函数的表示法
1.两个函数相同是指它们的 相同,且 完全一致.
2.在函数定义域中,任意的x∈A,在f的作用下,在B中都有唯一确定的f(x)与之对应.这可概述为: 和 .
3. 的定义域为
定义域
对应关系
存在性
唯一性
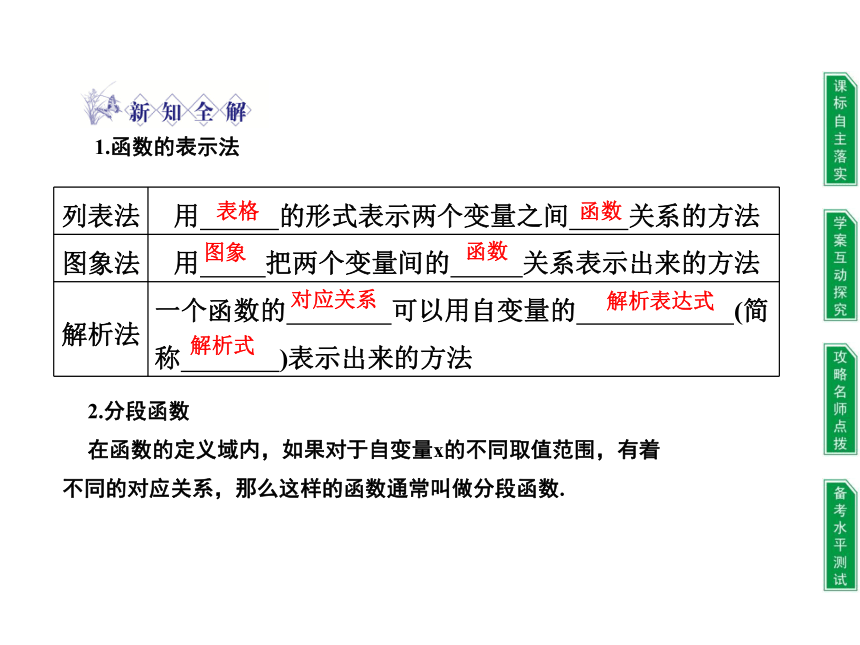
列表法 用 的形式表示两个变量之间 关系的方法
图象法 用 把两个变量间的 关系表示出来的方法
解析法 一个函数的 可以用自变量的 (简称 )表示出来的方法
1.函数的表示法
2.分段函数
在函数的定义域内,如果对于自变量x的不同取值范围,有着不同的对应关系,那么这样的函数通常叫做分段函数.
图象
函数
对应关系
解析表达式
解析式
表格
函数
每个函数都可以用列表法、图象法、解析式法三种形式表示吗?
【提示】 不一定,如函数y=x,x∈R,就无法用列表法表示.
求函数解析式
求下列函数的解析式:
(1)已知f(x+1)=x2-3x+2,求f(x);
(2)已知f( +1)=x+2 ,求f(x);
(3)已知f(x)=ax2+bx+c,若f(0)=0,且f(x+1)=f(x)+x+1,求f(x).
【思路点拨】 (1)(2)小题可以用换元法或配凑法,求a,b,c,利用条件
(1)中解法为直接变换法或称为配凑法,通过观察、分析,将右端“x2-3x+2”变为接受对象“x+1”的表达式,即变为含(x+1)的表达式,这种解法对变形能力、观察能力有一定的要求.
(2)中解法称为换元法,所谓换元法即将接受对象 “ +1“换作另一个字母“t”,然后从中解出x与t的关系,代入原式中便可求出关于“t”的函数关系,此即为所求函数解析式.但在利用这种方法时要注意自变量的取值范围的变化情况,否则就得不到正确的表达式.
(3)中解法称为待定系数法,我们只要清楚所求函数解析式的类型,便可设出其函数解析式,只要想法确定其系数即可求出结果.
1.求下列函数的解析式:
作函数的图象
作出下列函数的图象.
【思路点拨】 初中阶段我们已经知道,一次函数的图象是直线,二次函数图象是拋物线,反比例函数图象是双曲线.现在我们只要结合定义域,找到一些关键点,便可画出函数的大致图象.
【解析】 (1)当x=1时,y=1,所画函数图象如图1;
(2)y=x2-4x+3=(x-2)2-1,
且x=1,3时,y=0;
当x=2时,y=-1,
所画函数图象如图2.
图1 图2
图3
(1)图象法是表示函数的方法之一,画函数图象时,以定义域、对应关系为依据,采用列表、描点法作图.当已知式是一次或二次式时,可借助一次函数或二次函数的图象帮助作图.
(2)作图象时,应标出一些关键点.例如,图象的顶点、端点、与坐标轴的交点等.要分清这些关键点是实心点,还是空心点.
2.作出下列函数的图象.
【解析】 (1)此函数图象是直线y=x的一部分.
(2)此函数的定义域为{-2,-1,0,1,2},所以其图象由五个点组成,这些点都在直线y=1-x上.(这样的点叫做整点)
求分段函数的函数值
【思路点拨】
【解析】 ∵-1<0,∴f(-1)=0,
∴f(f(-1))=f(0)=?π?,∴f(f(f(-1)))=f(?π?)=?π?+1.
(1)分段函数求值,一定要注意所给自变量的值所在的范围,代入相应的解析式求得.
(2)象本题中含有多层“f”的问题,要按照“由里到外”的顺序,层层处理.
【解析】 (1)∵5>4,∴f(5)=-5+2=-3.∵-3<0,
∴f(f(5))=f(-3)=-3+4=1,
又∵0<1<4,∴f(f(f(5)))=f(1)=1-2=-1
(2)当a+4=-1时,a=-5<0,∴a=-5符合题意,
当a2-2a=-1时,a=1,
∵0<1<4,∴a=1符合题意;
当-a+2=-1时,a=3<4,
∴a=3不符合题意.∴a=-5或a=1.
优点 缺点
解
析
法 一是简明、全面地概括了变量间的关系;二是通过解析式可以求出任意一个自变量所对应的函数值 不够形象、直观、具体,而且并不是所有的函数都能用解析式表示出来
列
表
法 不需要计算就可以直接看出与自变量的值相对应的函数值 它只能表示自变量取较少的有限值的对应关系
图
象
法 能形象直观地表示出函数的变化情况 只能近似地求出自变量的值所对应的函数值,而且有时误差较大
1.函数的三种表示方法的优缺点比较
2.关于分段函数
(1)分段函数虽由几部分构成,但代表的是一个函数.只不过在定义域内的不同部分取值时,函数对应关系不同.其值域也是各段上的函数值集合的并集.
(2)求分段函数的有关函数值的关键是“分段归类”,即自变量的取值属于哪一段,就用哪一段的解析式.
(3)作分段函数的图象时,则应分段分别作出其图象,在作每一段图象时,先不管定义域的限制,用虚线作出其图象,再用实线保留定义域内的一段图象即可.
已知f(x2+2)=x4+4x2,求f(x)的解析式.
【错解】 ∵f(x2+2)=x4+4x2=(x2+2)2-4,
设t=x2+2,则f(t)=t2-4.∴f(x)=x2-4.
【错因】 本题错解的原因是忽略了函数f(x)的定义域.上面的解法,似乎是无懈可击,然而从其结论,即f(x)=x2-4来看,并未注明f(x)的定义域,那么按一般理解,就应认为其定义域是全体实数.但是f(x)=x2-4的定义域不是全体实数.
事实上,任何一个函数都由定义域、值域和对应关系f三要素组成.所以,当函数f(g(x))一旦给出,则其对应关系f就已确定并不可改变,那么f的“管辖范围”(即g(x)的值域)也就随之确定.因此,我们由f(g(x))求f(x)时,求得的f(x)的定义域就理应与f(g(x))中的f的“管辖范围”一致才妥.
【正解】 ∵f(x2+2)=x4+4x2=(x2+2)2-4,
令t=x2+2(t≥2),
则f(t)=t2-4(t≥2),
∴f(x)=x2-4(x≥2).
1.设f(x)=2x+3,g(x+2)=f(x),则g(x)等于 ( )
?A.?2x+1 ?B.?2x-1
?C.?2x-3 ? D.?2x+7
【解析】 由题意知g(x+2)=2x+3=2(x+2)-1,
∴g(x)=2x-1.故选B.
【答案】 ?B?
2.下列各图中,不能是函数f(x)图象的是 ( )
【答案】 ?C?
次数 1 2 3 4 5
分数 85 88 93 86 95
3.某班连续进行了5次数学测试,其中智方同学的成绩如表所示,在这个函数中,定义域是 ,值域是 .
【答案】 {1,2,3,4,5} {85,88,93,86,95}
笔记本数x 1 2 3 4 5
钱数(元) 5 10 15 20 25
4.某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})本笔记本需要y元,试用函数的三种表示法表示函数y=f(x).
【解析】 这个函数的定义域是数集{1,2,3,4,5}.用解析法表示函数y=f(x)为y=5x,x∈{1,2,3,4,5}.用列表法表示函数y=f(x)如表所示:
用图象法表示函数y=f(x)如图所示:
2.2 函数的表示法
1.两个函数相同是指它们的 相同,且 完全一致.
2.在函数定义域中,任意的x∈A,在f的作用下,在B中都有唯一确定的f(x)与之对应.这可概述为: 和 .
3. 的定义域为
定义域
对应关系
存在性
唯一性
列表法 用 的形式表示两个变量之间 关系的方法
图象法 用 把两个变量间的 关系表示出来的方法
解析法 一个函数的 可以用自变量的 (简称 )表示出来的方法
1.函数的表示法
2.分段函数
在函数的定义域内,如果对于自变量x的不同取值范围,有着不同的对应关系,那么这样的函数通常叫做分段函数.
图象
函数
对应关系
解析表达式
解析式
表格
函数
每个函数都可以用列表法、图象法、解析式法三种形式表示吗?
【提示】 不一定,如函数y=x,x∈R,就无法用列表法表示.
求函数解析式
求下列函数的解析式:
(1)已知f(x+1)=x2-3x+2,求f(x);
(2)已知f( +1)=x+2 ,求f(x);
(3)已知f(x)=ax2+bx+c,若f(0)=0,且f(x+1)=f(x)+x+1,求f(x).
【思路点拨】 (1)(2)小题可以用换元法或配凑法,求a,b,c,利用条件
(1)中解法为直接变换法或称为配凑法,通过观察、分析,将右端“x2-3x+2”变为接受对象“x+1”的表达式,即变为含(x+1)的表达式,这种解法对变形能力、观察能力有一定的要求.
(2)中解法称为换元法,所谓换元法即将接受对象 “ +1“换作另一个字母“t”,然后从中解出x与t的关系,代入原式中便可求出关于“t”的函数关系,此即为所求函数解析式.但在利用这种方法时要注意自变量的取值范围的变化情况,否则就得不到正确的表达式.
(3)中解法称为待定系数法,我们只要清楚所求函数解析式的类型,便可设出其函数解析式,只要想法确定其系数即可求出结果.
1.求下列函数的解析式:
作函数的图象
作出下列函数的图象.
【思路点拨】 初中阶段我们已经知道,一次函数的图象是直线,二次函数图象是拋物线,反比例函数图象是双曲线.现在我们只要结合定义域,找到一些关键点,便可画出函数的大致图象.
【解析】 (1)当x=1时,y=1,所画函数图象如图1;
(2)y=x2-4x+3=(x-2)2-1,
且x=1,3时,y=0;
当x=2时,y=-1,
所画函数图象如图2.
图1 图2
图3
(1)图象法是表示函数的方法之一,画函数图象时,以定义域、对应关系为依据,采用列表、描点法作图.当已知式是一次或二次式时,可借助一次函数或二次函数的图象帮助作图.
(2)作图象时,应标出一些关键点.例如,图象的顶点、端点、与坐标轴的交点等.要分清这些关键点是实心点,还是空心点.
2.作出下列函数的图象.
【解析】 (1)此函数图象是直线y=x的一部分.
(2)此函数的定义域为{-2,-1,0,1,2},所以其图象由五个点组成,这些点都在直线y=1-x上.(这样的点叫做整点)
求分段函数的函数值
【思路点拨】
【解析】 ∵-1<0,∴f(-1)=0,
∴f(f(-1))=f(0)=?π?,∴f(f(f(-1)))=f(?π?)=?π?+1.
(1)分段函数求值,一定要注意所给自变量的值所在的范围,代入相应的解析式求得.
(2)象本题中含有多层“f”的问题,要按照“由里到外”的顺序,层层处理.
【解析】 (1)∵5>4,∴f(5)=-5+2=-3.∵-3<0,
∴f(f(5))=f(-3)=-3+4=1,
又∵0<1<4,∴f(f(f(5)))=f(1)=1-2=-1
(2)当a+4=-1时,a=-5<0,∴a=-5符合题意,
当a2-2a=-1时,a=1,
∵0<1<4,∴a=1符合题意;
当-a+2=-1时,a=3<4,
∴a=3不符合题意.∴a=-5或a=1.
优点 缺点
解
析
法 一是简明、全面地概括了变量间的关系;二是通过解析式可以求出任意一个自变量所对应的函数值 不够形象、直观、具体,而且并不是所有的函数都能用解析式表示出来
列
表
法 不需要计算就可以直接看出与自变量的值相对应的函数值 它只能表示自变量取较少的有限值的对应关系
图
象
法 能形象直观地表示出函数的变化情况 只能近似地求出自变量的值所对应的函数值,而且有时误差较大
1.函数的三种表示方法的优缺点比较
2.关于分段函数
(1)分段函数虽由几部分构成,但代表的是一个函数.只不过在定义域内的不同部分取值时,函数对应关系不同.其值域也是各段上的函数值集合的并集.
(2)求分段函数的有关函数值的关键是“分段归类”,即自变量的取值属于哪一段,就用哪一段的解析式.
(3)作分段函数的图象时,则应分段分别作出其图象,在作每一段图象时,先不管定义域的限制,用虚线作出其图象,再用实线保留定义域内的一段图象即可.
已知f(x2+2)=x4+4x2,求f(x)的解析式.
【错解】 ∵f(x2+2)=x4+4x2=(x2+2)2-4,
设t=x2+2,则f(t)=t2-4.∴f(x)=x2-4.
【错因】 本题错解的原因是忽略了函数f(x)的定义域.上面的解法,似乎是无懈可击,然而从其结论,即f(x)=x2-4来看,并未注明f(x)的定义域,那么按一般理解,就应认为其定义域是全体实数.但是f(x)=x2-4的定义域不是全体实数.
事实上,任何一个函数都由定义域、值域和对应关系f三要素组成.所以,当函数f(g(x))一旦给出,则其对应关系f就已确定并不可改变,那么f的“管辖范围”(即g(x)的值域)也就随之确定.因此,我们由f(g(x))求f(x)时,求得的f(x)的定义域就理应与f(g(x))中的f的“管辖范围”一致才妥.
【正解】 ∵f(x2+2)=x4+4x2=(x2+2)2-4,
令t=x2+2(t≥2),
则f(t)=t2-4(t≥2),
∴f(x)=x2-4(x≥2).
1.设f(x)=2x+3,g(x+2)=f(x),则g(x)等于 ( )
?A.?2x+1 ?B.?2x-1
?C.?2x-3 ? D.?2x+7
【解析】 由题意知g(x+2)=2x+3=2(x+2)-1,
∴g(x)=2x-1.故选B.
【答案】 ?B?
2.下列各图中,不能是函数f(x)图象的是 ( )
【答案】 ?C?
次数 1 2 3 4 5
分数 85 88 93 86 95
3.某班连续进行了5次数学测试,其中智方同学的成绩如表所示,在这个函数中,定义域是 ,值域是 .
【答案】 {1,2,3,4,5} {85,88,93,86,95}
笔记本数x 1 2 3 4 5
钱数(元) 5 10 15 20 25
4.某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})本笔记本需要y元,试用函数的三种表示法表示函数y=f(x).
【解析】 这个函数的定义域是数集{1,2,3,4,5}.用解析法表示函数y=f(x)为y=5x,x∈{1,2,3,4,5}.用列表法表示函数y=f(x)如表所示:
用图象法表示函数y=f(x)如图所示:
