北师大版高中数学必修1《函数概念》教学课件(共24张PPT)
文档属性
| 名称 | 北师大版高中数学必修1《函数概念》教学课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 21:58:29 | ||
图片预览







文档简介
(共24张PPT)
§?2 对函数的进一步认识
2.1 函数概念
1.初中时你学过哪些函数?y=kx+b,(k≠0),y=ax2+bx+c,(a≠0),
(k≠0)分别叫 , , .
2.函数y=kx+b,已知kb<0,则函数的图象经过第
象限.
3.函数y=2x2+3x+1.当x=-1时的函数值为 .
一次函数
二次函数
反比例函数
一、二、四
或一、三、四
0
1.函数
(1)函数的定义
[JP2]给定两个 A和B,如果按照某个对应关系f,对于集合A中任何一个数x,在集合B中都存在 的数f(x)与之对应,那么就把对应关系f叫做定义在集合A上的函数,记作 或 .
(2)函数的定义域与值域
对于函数y=f(x),x∈A,其中x叫作自变量, 叫做函数的定义域,
叫做函数的值域 .
非空数集
唯一确定
f:A →B
y=f(x),x∈A
集合A
集合{f(x)|x∈A}
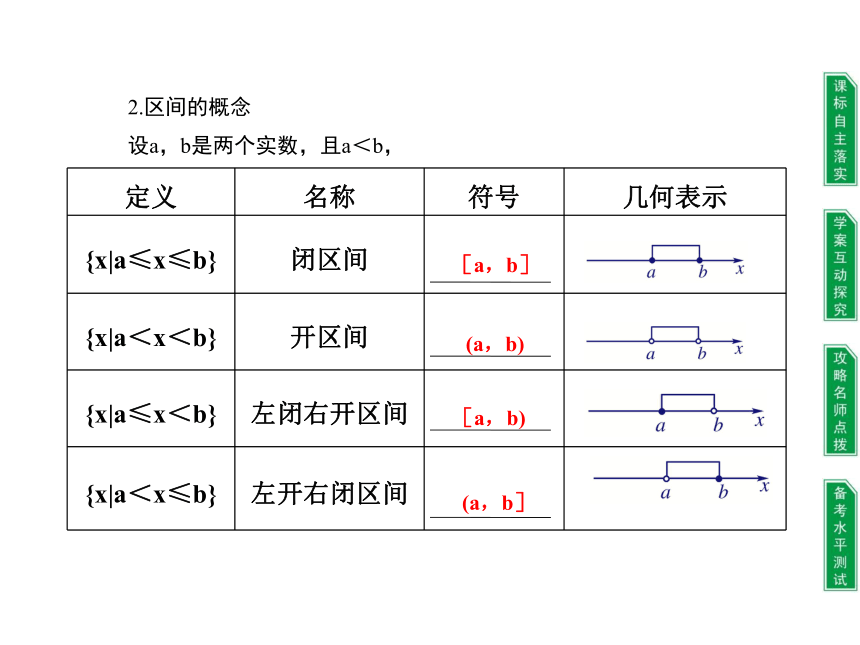
定义 名称 符号 几何表示
{x|a≤x≤b} 闭区间
{x|a<x<b} 开区间
{x|a≤x<b} 左闭右开区间
{x|a<x≤b} 左开右闭区间
2.区间的概念
设a,b是两个实数,且a<b,
[a,b]
(a,b)
[a,b)
(a,b]
定义 {x|x∈R} {x|x≥a} {x|x>a} {x|x≤a} {x|x<a}
符号
3.无穷大概念
(1)实数集R用区间表示为 ,“∞”读作 ,“-∞”读作 ,“+∞”读作 .
(2)无穷区间的表示
(-∞,+∞)
无穷大
负无穷大
正无穷大
(-∞,+∞)
[a,+∞)
(a,+∞)
(-∞,a]
(-∞,a)
1.什么样的对应可以构成函数?
【提示】 函数的定义中“任一x”与“有唯一确定的y”说明函数中两变量x、y是“一对一”或“多对一”时可以构成函数.
2.f(x)与f(a)的含义有何不同?
【提示】 f(x)与f(a)的区别与联系:f(a)表示当x=a时函数f(x)的值,是一个常量,而f(x)是自变量x的函数,表示的是变量.
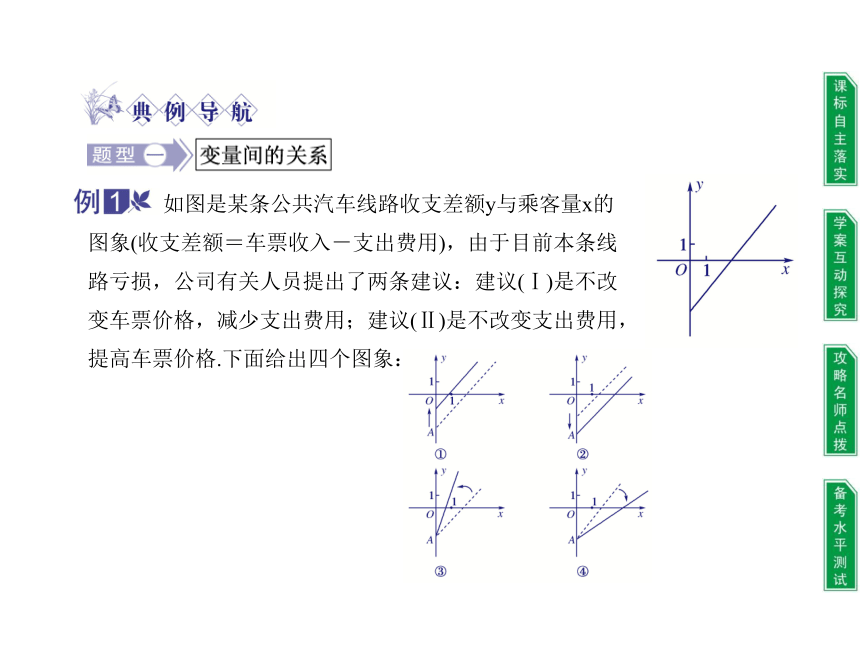
如图是某条公共汽车线路收支差额y与乘客量x的
图象(收支差额=车票收入-支出费用),由于目前本条线
路亏损,公司有关人员提出了两条建议:建议(Ⅰ)是不改
变车票价格,减少支出费用;建议(Ⅱ)是不改变支出费用,
提高车票价格.下面给出四个图象:
在这些图象中 ( )
?A.?①反映了建议(Ⅱ),③反映了建议(Ⅰ)
?B.?①反映了建议(Ⅰ),③反映了建议(Ⅱ)
?C.?②反映了建议(Ⅰ),④反映了建议(Ⅱ)
?D.?④反映了建议(Ⅰ),②反映了建议(Ⅱ)
【思路点拨】 解答本题应从y与x的关系出发,分析出票价与斜率的关系,然后就(Ⅰ),(Ⅱ)两种建议分别描出图象,与题中①、②、③、④对应便可求解.
【解析】 由题可知直线与y轴交点的纵坐标的相反数表示支出,斜率表示票价,建议(Ⅰ)中票价不变,即直线的斜率不变;减少支出即直线与y轴交点纵坐标变大,对应①.建议(Ⅱ)中,直线与y轴交点的纵坐标不变,斜率变大,对应③.
【答案】 ?B?
(1)解答此类题目的关键在于借助变量间的图象分析实际问题中所隐含的东西,然后结合已学知识加以综合分析,从而把问题解决.
(2)判断两变量之间是否为函数关系,关键是看变量之间的关系是否为确定的关系,如③中收入与消费支出的关系是一种趋势而非确定关系,而其余均为确定关系.
1.下列各组中两个变量之间是否存在依赖关系?其中哪些
是函数关系?
①球的体积和它的半径;
②速度不变的情况下,汽车行驶的路程与行驶时间;
③家庭收入愈多,其消费支出也有增长的趋势;
④正三角形的面积和它的边长.
【解析】 ①②③④中两个变量间都存在依赖关系,其中①②④是函数关系.
下列各组中的两个函数是否表示同一函数.
【思路点拨】 逐一考查两个函数的定义域,对应关系和值域.
【解析】 (1)两个函数定义域显然不同,故两个函数不表示同一函数.
(2)两个函数的对应关系显然不同,故两个函数不表示同一函数.
(3)两个函数的定义域显然不同,故两个函数不表示同一函数.
(4)定义域、对应关系、值域均相同,两个函数表示同一函数.
(5)定义域、对应关系、值域均相同,两个函数表示同一函数.
(6)定义域、对应关系、值域均相同,两个函数表示同一函数.
只有定义域、值域和对应关系都相同的两个函数才是同一函数,三者中只要有一个不同就不是同一函数.容易知道,定义域和对应关系相同的两个函数的值域也一定相同.
2.试判断以下各组函数是否是相等函数:
【解析】 (1)定义域相同,都是R,但是g(x)=|x|,即它们的解析式不同,也就是对应关系不同,故不相等.
(2)f(x)==x+3(x≠3),它与g(x)=x+3的定义域不同,故不是相等函数.
(3)定义域相同,都是R,但是它们的解析式不同,也就是对应关系不同,故不相等.
(4)f(x)的定义域是{x|x≠1},g(x)的定义域是R,它们的定义域不同,故不相等.
求下列函数的定义域
【思路点拨】
定义域的求法:
(1)如果f(x)是整式,那么函数的定义域是实数集R;
(2)如果f(x)是分式,那么函数的定义域是使分母不为0的实数的集合;
(3)如果f(x)为偶次根式,那么函数的定义域是使根号内的式子大于或等于0的实数的集合;
(4)如果f(x)是由几个部分的数学式子构成的,那么函数的定义域是使各部分式子都有意义的实数的集合.
(5)如果函数有实际背景,那么除符合上述要求外,还要符合实际情况.
函数定义域要用集合或区间形式表示,这一点初学者易忽视.
3.求下列函数的定义域:
【解析】 (1)由题意知4+x≥0,∴x≥-4,故f(x)的定义域是{x|x≥-4}.
(2)由1-x≥0且1+x≠0,得x≤1且x≠-1,故f(x)的定义域是{x|x≤1且x≠-1}.
【思路点拨】 直接将自变量x的取值代入函数解析式进行计算.
(1)当x的取值用字母表示时,对应的函数值也用字母表示,但要注意化简.
(2)当求多重函数值时,一般要由里到外逐步计算.
1.准确理解函数概念
(1)对应法则f是表示定义域和值域的一种对应关系,与所选择的字母无关.在研究函数时,除用符号f(x)外,还常用g(x),F(x),G(x)等符号来表示.变量也不是用唯一的字母来表示,f(x)=x+1与f(t)=t+1是同一个函数.
(2)符号y=f(x)是“y是x的函数”的数学表示,应理解为:x是自变量,它是对应法则所施加的对象;f是对应法则,它既可以是解析式,也可以是图象、表格或文字描述.y=f(x)仅仅是函数符号,不能认为“y等于f与x的乘积”.
(3)虽然f(x)=x2和f(x-1)=x2等号右边的表达式都是x2,但是,由于对应法则f所施加的对象不同(一个为x,而另一个为x-1),因此函数的解析式是不同的.
(4)f(a)与f(x)的关系:f(a)表示当x=a时函数f(x)的值,是一个常量.而f(x)是自变量x的函数,表示的是变量.
2.正确使用区间符号
区间是某些数集的一种重要表示形式,具有简单直观的优点,因此是表示函数的定义域、值域及不等式解集的重要工具.应用时一定要弄清各种区间的含义及它们的区别,如[-1,1]表示{x|-1≤x≤1},而[-1,1)表示{x|-1≤x<1}等.
【注意】 (1)无穷大是一个符号,不是一个具体的数;(2)若[a,b]是确定区间,则一定有a<b.
【错因】 求函数定义域时,不能先进行变形,否则,会使定义域发生改变,造成错误.因此,必须根据原始函数解析式来求定义域.
【解析】 对于?A?,∵-x2-1<0,∴根式无意义,不表示函数;
对于?B?,当x=0时对应的函数值有两个,不符合函数的定义;
对于?D?,任意x,与x对应的y值不唯一,因此也不表示函数.
【答案】 ?C?
2.下列变量间的关系是函数关系的是 ( )
?A.?匀速航行的轮船在2小时内航行的路程
?B.?某地蔬菜的价格与蔬菜的供应量的关系
?C.?正方形的面积S与其边长a之间的关系
?D.?光照时间和果树的亩产量
【解析】 ?A是常量,B是依赖关系,C是函数关系,D是依赖关系?.
【答案】 ?C?
3.函数g(x)=2x+1,x∈{1,2,3,4}的值域是 .
【答案】 {3,5,7,9}
4.已知函数f(x)=x2+x-1.
(1)求f(2), .
(2)若f(x)=5,求x
【解析】 (1)f(2)=22+2-1=5,
.
(2)∵f(x)=x2+x-1=5,
∴x2+x-6=0,∴x=2或x=-3.
§?2 对函数的进一步认识
2.1 函数概念
1.初中时你学过哪些函数?y=kx+b,(k≠0),y=ax2+bx+c,(a≠0),
(k≠0)分别叫 , , .
2.函数y=kx+b,已知kb<0,则函数的图象经过第
象限.
3.函数y=2x2+3x+1.当x=-1时的函数值为 .
一次函数
二次函数
反比例函数
一、二、四
或一、三、四
0
1.函数
(1)函数的定义
[JP2]给定两个 A和B,如果按照某个对应关系f,对于集合A中任何一个数x,在集合B中都存在 的数f(x)与之对应,那么就把对应关系f叫做定义在集合A上的函数,记作 或 .
(2)函数的定义域与值域
对于函数y=f(x),x∈A,其中x叫作自变量, 叫做函数的定义域,
叫做函数的值域 .
非空数集
唯一确定
f:A →B
y=f(x),x∈A
集合A
集合{f(x)|x∈A}
定义 名称 符号 几何表示
{x|a≤x≤b} 闭区间
{x|a<x<b} 开区间
{x|a≤x<b} 左闭右开区间
{x|a<x≤b} 左开右闭区间
2.区间的概念
设a,b是两个实数,且a<b,
[a,b]
(a,b)
[a,b)
(a,b]
定义 {x|x∈R} {x|x≥a} {x|x>a} {x|x≤a} {x|x<a}
符号
3.无穷大概念
(1)实数集R用区间表示为 ,“∞”读作 ,“-∞”读作 ,“+∞”读作 .
(2)无穷区间的表示
(-∞,+∞)
无穷大
负无穷大
正无穷大
(-∞,+∞)
[a,+∞)
(a,+∞)
(-∞,a]
(-∞,a)
1.什么样的对应可以构成函数?
【提示】 函数的定义中“任一x”与“有唯一确定的y”说明函数中两变量x、y是“一对一”或“多对一”时可以构成函数.
2.f(x)与f(a)的含义有何不同?
【提示】 f(x)与f(a)的区别与联系:f(a)表示当x=a时函数f(x)的值,是一个常量,而f(x)是自变量x的函数,表示的是变量.
如图是某条公共汽车线路收支差额y与乘客量x的
图象(收支差额=车票收入-支出费用),由于目前本条线
路亏损,公司有关人员提出了两条建议:建议(Ⅰ)是不改
变车票价格,减少支出费用;建议(Ⅱ)是不改变支出费用,
提高车票价格.下面给出四个图象:
在这些图象中 ( )
?A.?①反映了建议(Ⅱ),③反映了建议(Ⅰ)
?B.?①反映了建议(Ⅰ),③反映了建议(Ⅱ)
?C.?②反映了建议(Ⅰ),④反映了建议(Ⅱ)
?D.?④反映了建议(Ⅰ),②反映了建议(Ⅱ)
【思路点拨】 解答本题应从y与x的关系出发,分析出票价与斜率的关系,然后就(Ⅰ),(Ⅱ)两种建议分别描出图象,与题中①、②、③、④对应便可求解.
【解析】 由题可知直线与y轴交点的纵坐标的相反数表示支出,斜率表示票价,建议(Ⅰ)中票价不变,即直线的斜率不变;减少支出即直线与y轴交点纵坐标变大,对应①.建议(Ⅱ)中,直线与y轴交点的纵坐标不变,斜率变大,对应③.
【答案】 ?B?
(1)解答此类题目的关键在于借助变量间的图象分析实际问题中所隐含的东西,然后结合已学知识加以综合分析,从而把问题解决.
(2)判断两变量之间是否为函数关系,关键是看变量之间的关系是否为确定的关系,如③中收入与消费支出的关系是一种趋势而非确定关系,而其余均为确定关系.
1.下列各组中两个变量之间是否存在依赖关系?其中哪些
是函数关系?
①球的体积和它的半径;
②速度不变的情况下,汽车行驶的路程与行驶时间;
③家庭收入愈多,其消费支出也有增长的趋势;
④正三角形的面积和它的边长.
【解析】 ①②③④中两个变量间都存在依赖关系,其中①②④是函数关系.
下列各组中的两个函数是否表示同一函数.
【思路点拨】 逐一考查两个函数的定义域,对应关系和值域.
【解析】 (1)两个函数定义域显然不同,故两个函数不表示同一函数.
(2)两个函数的对应关系显然不同,故两个函数不表示同一函数.
(3)两个函数的定义域显然不同,故两个函数不表示同一函数.
(4)定义域、对应关系、值域均相同,两个函数表示同一函数.
(5)定义域、对应关系、值域均相同,两个函数表示同一函数.
(6)定义域、对应关系、值域均相同,两个函数表示同一函数.
只有定义域、值域和对应关系都相同的两个函数才是同一函数,三者中只要有一个不同就不是同一函数.容易知道,定义域和对应关系相同的两个函数的值域也一定相同.
2.试判断以下各组函数是否是相等函数:
【解析】 (1)定义域相同,都是R,但是g(x)=|x|,即它们的解析式不同,也就是对应关系不同,故不相等.
(2)f(x)==x+3(x≠3),它与g(x)=x+3的定义域不同,故不是相等函数.
(3)定义域相同,都是R,但是它们的解析式不同,也就是对应关系不同,故不相等.
(4)f(x)的定义域是{x|x≠1},g(x)的定义域是R,它们的定义域不同,故不相等.
求下列函数的定义域
【思路点拨】
定义域的求法:
(1)如果f(x)是整式,那么函数的定义域是实数集R;
(2)如果f(x)是分式,那么函数的定义域是使分母不为0的实数的集合;
(3)如果f(x)为偶次根式,那么函数的定义域是使根号内的式子大于或等于0的实数的集合;
(4)如果f(x)是由几个部分的数学式子构成的,那么函数的定义域是使各部分式子都有意义的实数的集合.
(5)如果函数有实际背景,那么除符合上述要求外,还要符合实际情况.
函数定义域要用集合或区间形式表示,这一点初学者易忽视.
3.求下列函数的定义域:
【解析】 (1)由题意知4+x≥0,∴x≥-4,故f(x)的定义域是{x|x≥-4}.
(2)由1-x≥0且1+x≠0,得x≤1且x≠-1,故f(x)的定义域是{x|x≤1且x≠-1}.
【思路点拨】 直接将自变量x的取值代入函数解析式进行计算.
(1)当x的取值用字母表示时,对应的函数值也用字母表示,但要注意化简.
(2)当求多重函数值时,一般要由里到外逐步计算.
1.准确理解函数概念
(1)对应法则f是表示定义域和值域的一种对应关系,与所选择的字母无关.在研究函数时,除用符号f(x)外,还常用g(x),F(x),G(x)等符号来表示.变量也不是用唯一的字母来表示,f(x)=x+1与f(t)=t+1是同一个函数.
(2)符号y=f(x)是“y是x的函数”的数学表示,应理解为:x是自变量,它是对应法则所施加的对象;f是对应法则,它既可以是解析式,也可以是图象、表格或文字描述.y=f(x)仅仅是函数符号,不能认为“y等于f与x的乘积”.
(3)虽然f(x)=x2和f(x-1)=x2等号右边的表达式都是x2,但是,由于对应法则f所施加的对象不同(一个为x,而另一个为x-1),因此函数的解析式是不同的.
(4)f(a)与f(x)的关系:f(a)表示当x=a时函数f(x)的值,是一个常量.而f(x)是自变量x的函数,表示的是变量.
2.正确使用区间符号
区间是某些数集的一种重要表示形式,具有简单直观的优点,因此是表示函数的定义域、值域及不等式解集的重要工具.应用时一定要弄清各种区间的含义及它们的区别,如[-1,1]表示{x|-1≤x≤1},而[-1,1)表示{x|-1≤x<1}等.
【注意】 (1)无穷大是一个符号,不是一个具体的数;(2)若[a,b]是确定区间,则一定有a<b.
【错因】 求函数定义域时,不能先进行变形,否则,会使定义域发生改变,造成错误.因此,必须根据原始函数解析式来求定义域.
【解析】 对于?A?,∵-x2-1<0,∴根式无意义,不表示函数;
对于?B?,当x=0时对应的函数值有两个,不符合函数的定义;
对于?D?,任意x,与x对应的y值不唯一,因此也不表示函数.
【答案】 ?C?
2.下列变量间的关系是函数关系的是 ( )
?A.?匀速航行的轮船在2小时内航行的路程
?B.?某地蔬菜的价格与蔬菜的供应量的关系
?C.?正方形的面积S与其边长a之间的关系
?D.?光照时间和果树的亩产量
【解析】 ?A是常量,B是依赖关系,C是函数关系,D是依赖关系?.
【答案】 ?C?
3.函数g(x)=2x+1,x∈{1,2,3,4}的值域是 .
【答案】 {3,5,7,9}
4.已知函数f(x)=x2+x-1.
(1)求f(2), .
(2)若f(x)=5,求x
【解析】 (1)f(2)=22+2-1=5,
.
(2)∵f(x)=x2+x-1=5,
∴x2+x-6=0,∴x=2或x=-3.
