2021--2022学年人教版九年级数学下册:29.1投影经典题型 课件(共48张PPT)
文档属性
| 名称 | 2021--2022学年人教版九年级数学下册:29.1投影经典题型 课件(共48张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 07:35:23 | ||
图片预览


文档简介
(共48张PPT)
投影经典题型总结
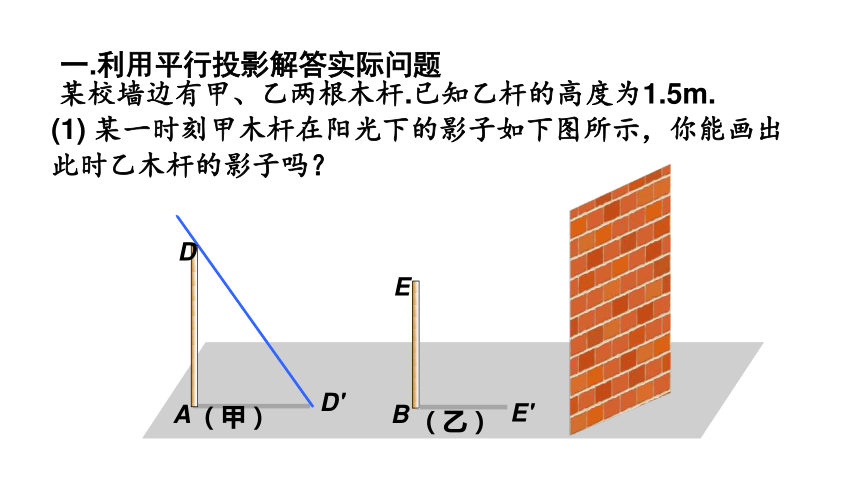
某校墙边有甲、乙两根木杆.已知乙杆的高度为1.5m.
(1) 某一时刻甲木杆在阳光下的影子如下图所示,你能画出此时乙木杆的影子吗?
A
(甲)
(乙)
D'
B
E'
D
E
一.利用平行投影解答实际问题
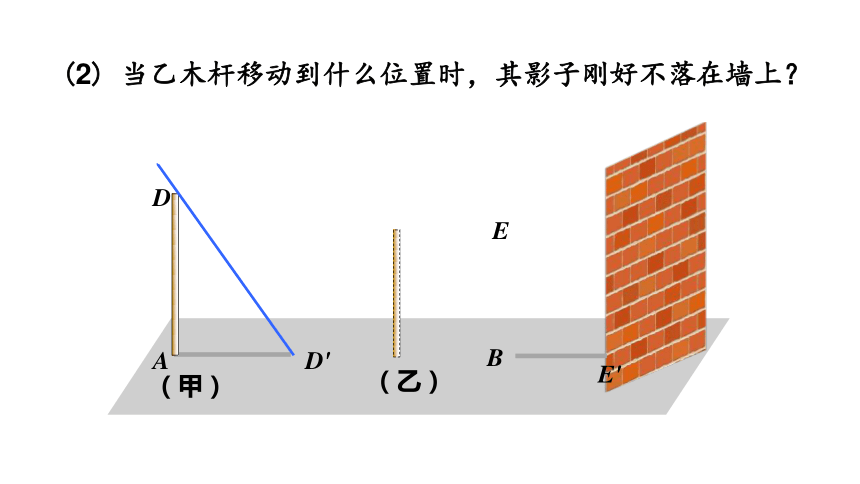
(2) 当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(甲)
(乙)
A
D
D'
B
E
E'
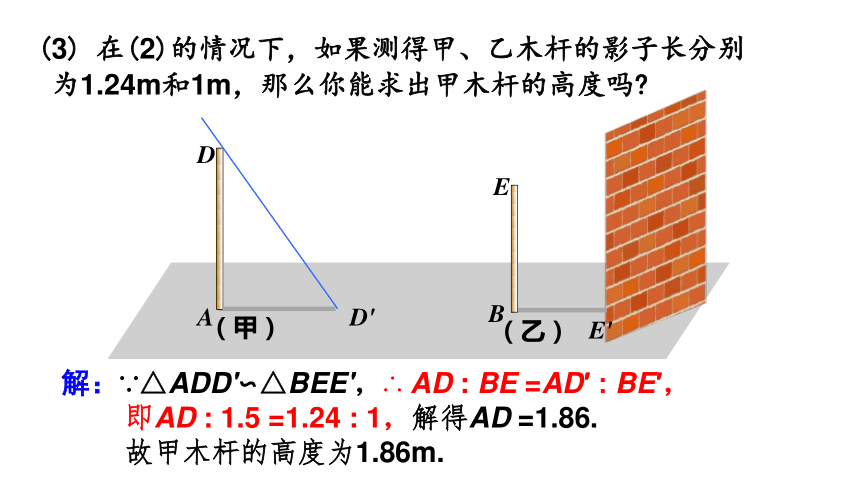
(3) 在(2)的情况下,如果测得甲、乙木杆的影子长分别
为1.24m和1m,那么你能求出甲木杆的高度吗
(甲)
(乙)
A
D
D'
B
E
E'
解:∵△ADD'∽△BEE',∴ AD : BE =AD′ : BE′,
即AD : 1.5 =1.24 : 1,解得AD =1.86.
故甲木杆的高度为1.86m.
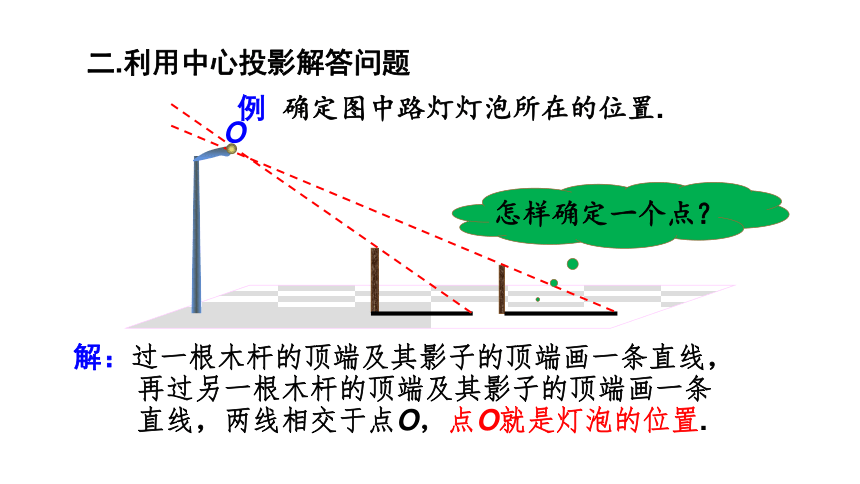
例 确定图中路灯灯泡所在的位置.
O
怎样确定一个点?
二.利用中心投影解答问题
解:过一根木杆的顶端及其影子的顶端画一条直线,
再过另一根木杆的顶端及其影子的顶端画一条
直线,两线相交于点O,点O就是灯泡的位置.
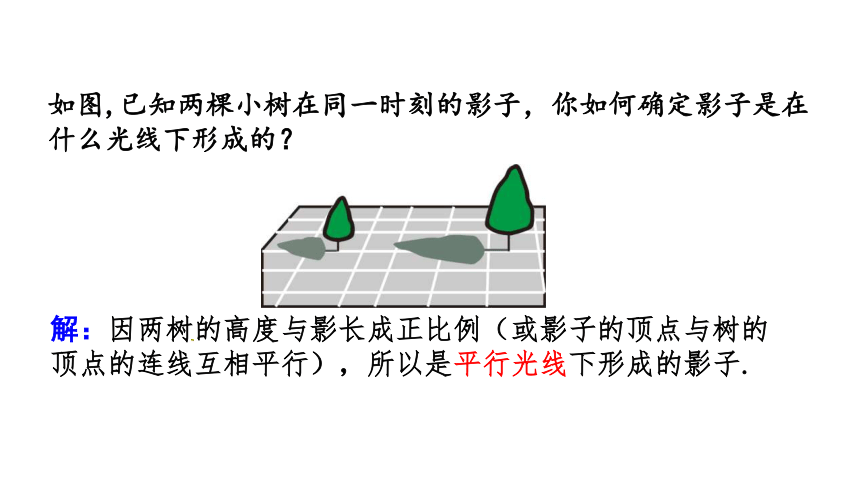
如图,已知两棵小树在同一时刻的影子,你如何确定影子是在什么光线下形成的?
解:因两树的高度与影长成正比例(或影子的顶点与树的顶点的连线互相平行),所以是平行光线下形成的影子.
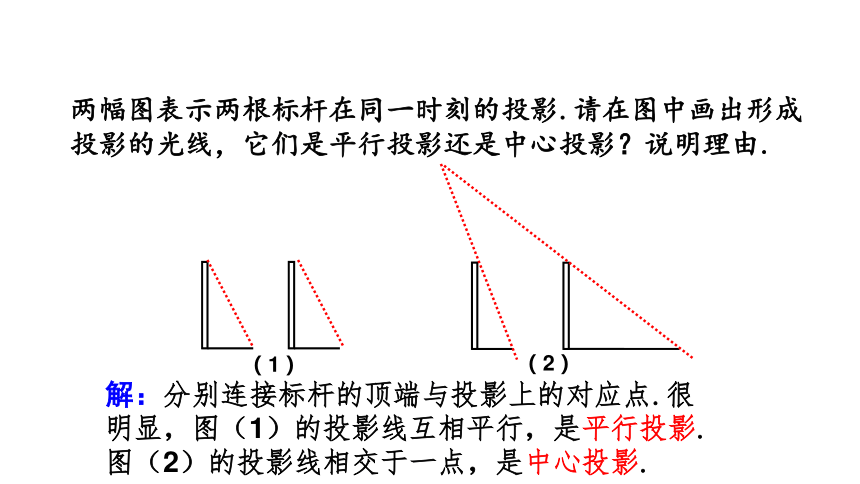
两幅图表示两根标杆在同一时刻的投影.请在图中画出形成投影的光线,它们是平行投影还是中心投影?说明理由.
解:分别连接标杆的顶端与投影上的对应点.很明显,图(1)的投影线互相平行,是平行投影.图(2)的投影线相交于一点,是中心投影.
(1)
(2)
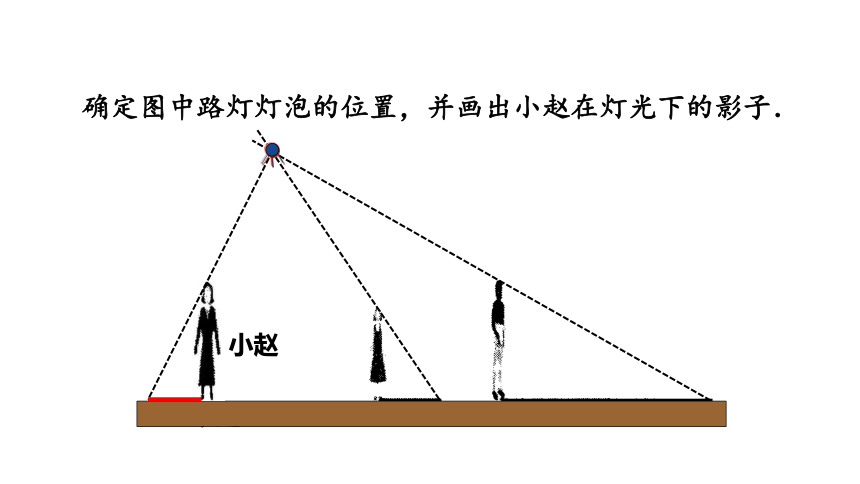
确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
小赵
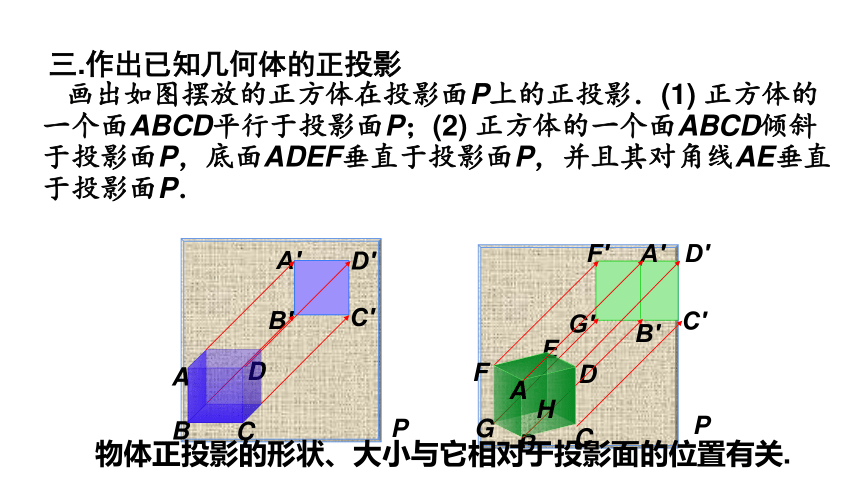
画出如图摆放的正方体在投影面P上的正投影.(1) 正方体的一个面ABCD平行于投影面P;(2) 正方体的一个面ABCD倾斜于投影面P,底面ADEF垂直于投影面P,并且其对角线AE垂直于投影面P.
A
B
C
D
A′
B′
C′
D′
P
B
C
D
E
F
G
F′
A′
D′
C′
B′
G′
P
A
H
物体正投影的形状、大小与它相对于投影面的位置有关.
三.作出已知几何体的正投影
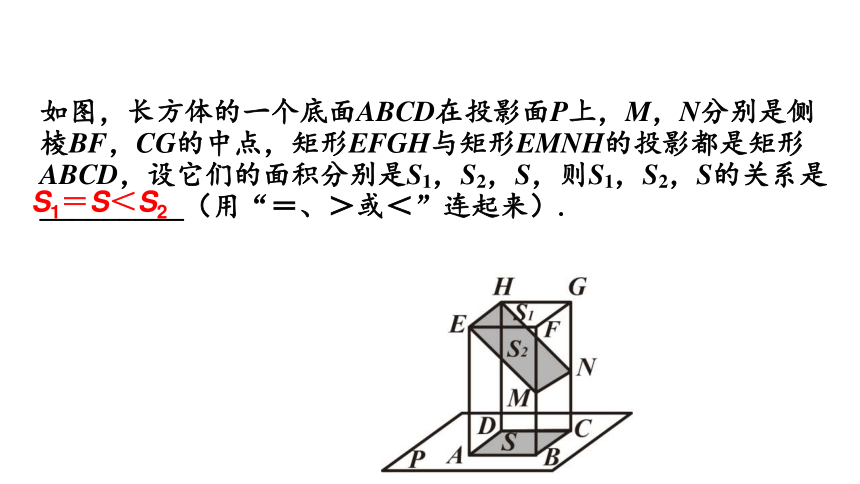
如图,长方体的一个底面ABCD在投影面P上,M,N分别是侧棱BF,CG的中点,矩形EFGH与矩形EMNH的投影都是矩形ABCD,设它们的面积分别是S1,S2,S,则S1,S2,S的关系是_________(用“=、>或<”连起来).
S1=S<S2
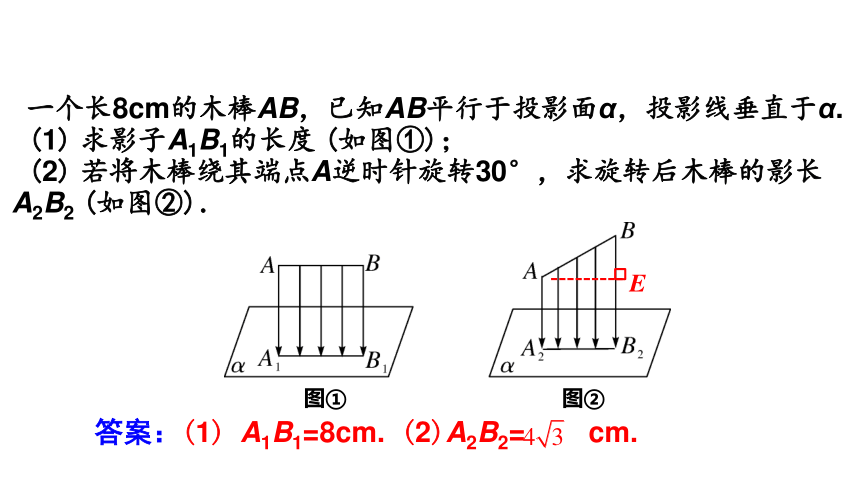
一个长8cm的木棒AB,已知AB平行于投影面α,投影线垂直于α.
(1) 求影子A1B1的长度 (如图①);
(2) 若将木棒绕其端点A逆时针旋转30°,求旋转后木棒的影长A2B2 (如图②).
答案:(1) A1B1=8cm.
E
(2)A2B2= cm.
图①
图②
画出图中基本几何体的三视图:
四.已知简单几何体画三视图
圆柱(1)
正三棱柱 (2)
球
(3)
主视图
宽
左视图
解:如图所示:
俯视图
主视图
左视图
俯视图
圆柱(1)
正三棱柱 (2)
球
(3)
3. 在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”;
1. 确定主视图的位置,画出主视图;
2. 在主视图正下方画出俯视图,注
意与主视图“长对正”;
三视图的具体画法为:
主视图
俯视图
左视图
高
长
宽
宽
注:可见的轮廓线画成实线;不可见的轮廓线,画成虚线.
归纳:
4. 为表示圆柱、圆锥等的对称轴,规定在视图中加画点划线( )表示对称轴.
画出半球和圆锥的三视图.
半球
主视图
俯视图
左视图
圆锥
主视图
俯视图
左视图
·.
画出如图所示的支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.
解:下图是支架的三视图.
主视图
俯视图
左视图
五.已知较复杂几何体画三视图
提示:长对正,高平齐,宽相等,不可见的轮廓线,用虚线画出.
画出该几何体的三视图.
六.作几何组合体的三视图
分析:这是一个圆柱体的组合体,从不同角度看它时,会呈现不同的视图,为全面地反映立体图形的现状,画图时规定:
看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
主视图
左视图
俯视图
解:下图是组合体的三视图.
画出图中简单组合体的三视图:
主视图
左视图
俯视图
解:三视图如下:
画出图中的几何体的三视图.
解:如图所示:
下图是一根钢管的直观图,画出它的三视图.
解:钢管的三视图为:
主视图
俯视图
左视图
如图,分别根据三视图(1) (2)说出立体图形的名称.
图(2)
图(1)
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
七.根据三视图描述较简单物体的形状
解:(1)从三个方向看立体图形,视图都是矩形,可以想
象出:整体是 ,如图1所示.
(2)从正面、侧面看立体图形,视图都是等腰三角形; 从上面看,视图是圆;可以想象出:整体是 ,如图2所示.
长方体
圆锥
图1
图2
由三视图想象实物现状:
实物
实物
根据物体的三视图描述物体的形状.
分析:由主视图可知,物体的正面是正五边形;由俯视图可知,由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱 (中间的实线表示),可见到,另有两条棱 (虚线表示) 被遮挡;由左视图可知,物体左侧有两个面的视图是矩形,它们的交线是一条棱 (中间的实线表示),可见到.综合各视图可知,物体的形状是正五棱柱.
八.根据三视图描述较复杂物体的形状
主视图
俯视图
左视图
解:物体是正五棱柱形状的,如图所示.
【方法总结】由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面的局部形状,然后再综合起来考虑整体图形.
根据下列物体的三视图,填出几何体的名称:
(1) 如图①所示的几何体是__________;
(2) 如图②所示的几何体是_________.
图①
图②
六棱柱
圆台
左视图
左视图
俯视图
俯视图
主视图
主视图
主视图
左视图
俯视图
请根据下面提供的三视图,画出几何图形.
九.根据三视图画出几何体的图形
解:如下图所示:
(1) 主视图
左视图
俯视图
请根据下面提供的三视图,画出几何图形.
解:如下图所示:
请根据下面提供的三视图,画出几何图形.
(2) 主视图
左视图
俯视图
解:如下图所示:
(1) 一个几何体的主视图和左视图如图所示,请补画这个几
何体的俯视图.
(2) 一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.
左视图
主视图
俯视图
主视图
俯视图
左视图
解:如图所示:
解:如图所示:
(1)
根据三视图画出实物图形.
解:如下图所示:
(2)
解:如下图所示:
(3)
解:如下图所示:
分析:
1. 应先由三视图想象出
;
2. 画出物体的 .
密封罐的立体形状
展开图
某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位:mm).
十.利用三视图求物体的表面积
解:由三视图可知,密封罐的形状是正六棱柱.
50mm
50mm
密封罐的高为50mm,底面正六边形的直径为100mm,边长
为50mm,
100mm
如图,是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为
如图是一个几何体的三视图,试描绘出这个零件的形状,并求出此三视图所描述的几何体的表面积.
解:该几何体是一个组合体,上部是一个圆锥,下部是一个圆柱,该几何体的表面积为
π×22+2π×2×2+ ×4×4π=20 π.
主视图
左视图
俯视图
4
2
一个机器零件的三视图如图所示(单位:cm),这个机器零件是一个什么样的立体图形?它的体积是多少?
15
10
主视图
12
15
左视图
10
俯视图
解:长方体,其体积为10×12×15=1800(cm3).
十一.利用三视图求物体的体积
分析:由三视图可知该几何体是长方体.长方体的长、宽、高分别是10cm、12cm、15cm,然后利用长方体的体积公式即可.
12
已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为 .
解析:根据三视图得到圆锥的底面圆的直径为8,即底面圆的半径r为4,圆锥的高为3,
所以圆锥的母线长 ,
所以这个圆锥的侧面积是π×4×5=20π.
20π
3
8
主
视
图
左
视
图
俯
视
图
8
8
13
如图是一个几何体的三视图.根据图示,可计算出该几何体的侧面积为 .
104π
如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为 cm2.
2π
主视图
左视图
俯视图
如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
分析:由三视图可知该几何体是
由圆柱、长方体组合而成.分别
计算它们的表面积和体积,然后
相加即可.
主视图
左视图
俯视图
解:该图形上、下部分分别是圆柱、长方体,根据图中数据得:
体积为
25×30×40+102×32π
=(30000+3200π)(cm3).
表面积为
20π×32+(30×40+25×40+25×30)×2
=(5900+640π)(cm2),
30cm
20cm
25cm
32cm
40cm
如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图.
(1) 请写出构成这个几何体的正方体的个数为 ;
(2) 计算这个几何体的表面积为 .
5
20cm2
主视图
左视图
俯视图
某一空间图形的三视图如图所示,其中主视图是半径为1的半圆以及高为 1 的矩形;左视图是半径为1的四分之一圆以及高为1的矩形;俯视图是半径为1的圆,求此图形的体积 (参考公式:V球= πR 3).
主视图
左视图
俯视图
由三视图可得,下部圆柱的底面半径为1,高为1,则V圆柱=π,上部 球的半径为1,则 V球= ,故此几何体的体积为 .
主视图
左视图
俯视图
解:由已知可得该几何体是一个下部为圆柱,上部为 球的组合体.
1. 三种图形的转化:
2. 由三视图求立体图形的体积 (或面积) 的方法:
(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等;
(2) 根据已知数据,求出立体图形的体积 (或将立体图形展开成一个平面图形,求出展开图的面积).
三视图
立体图
展开图
投影经典题型总结
某校墙边有甲、乙两根木杆.已知乙杆的高度为1.5m.
(1) 某一时刻甲木杆在阳光下的影子如下图所示,你能画出此时乙木杆的影子吗?
A
(甲)
(乙)
D'
B
E'
D
E
一.利用平行投影解答实际问题
(2) 当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(甲)
(乙)
A
D
D'
B
E
E'
(3) 在(2)的情况下,如果测得甲、乙木杆的影子长分别
为1.24m和1m,那么你能求出甲木杆的高度吗
(甲)
(乙)
A
D
D'
B
E
E'
解:∵△ADD'∽△BEE',∴ AD : BE =AD′ : BE′,
即AD : 1.5 =1.24 : 1,解得AD =1.86.
故甲木杆的高度为1.86m.
例 确定图中路灯灯泡所在的位置.
O
怎样确定一个点?
二.利用中心投影解答问题
解:过一根木杆的顶端及其影子的顶端画一条直线,
再过另一根木杆的顶端及其影子的顶端画一条
直线,两线相交于点O,点O就是灯泡的位置.
如图,已知两棵小树在同一时刻的影子,你如何确定影子是在什么光线下形成的?
解:因两树的高度与影长成正比例(或影子的顶点与树的顶点的连线互相平行),所以是平行光线下形成的影子.
两幅图表示两根标杆在同一时刻的投影.请在图中画出形成投影的光线,它们是平行投影还是中心投影?说明理由.
解:分别连接标杆的顶端与投影上的对应点.很明显,图(1)的投影线互相平行,是平行投影.图(2)的投影线相交于一点,是中心投影.
(1)
(2)
确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
小赵
画出如图摆放的正方体在投影面P上的正投影.(1) 正方体的一个面ABCD平行于投影面P;(2) 正方体的一个面ABCD倾斜于投影面P,底面ADEF垂直于投影面P,并且其对角线AE垂直于投影面P.
A
B
C
D
A′
B′
C′
D′
P
B
C
D
E
F
G
F′
A′
D′
C′
B′
G′
P
A
H
物体正投影的形状、大小与它相对于投影面的位置有关.
三.作出已知几何体的正投影
如图,长方体的一个底面ABCD在投影面P上,M,N分别是侧棱BF,CG的中点,矩形EFGH与矩形EMNH的投影都是矩形ABCD,设它们的面积分别是S1,S2,S,则S1,S2,S的关系是_________(用“=、>或<”连起来).
S1=S<S2
一个长8cm的木棒AB,已知AB平行于投影面α,投影线垂直于α.
(1) 求影子A1B1的长度 (如图①);
(2) 若将木棒绕其端点A逆时针旋转30°,求旋转后木棒的影长A2B2 (如图②).
答案:(1) A1B1=8cm.
E
(2)A2B2= cm.
图①
图②
画出图中基本几何体的三视图:
四.已知简单几何体画三视图
圆柱(1)
正三棱柱 (2)
球
(3)
主视图
宽
左视图
解:如图所示:
俯视图
主视图
左视图
俯视图
圆柱(1)
正三棱柱 (2)
球
(3)
3. 在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”;
1. 确定主视图的位置,画出主视图;
2. 在主视图正下方画出俯视图,注
意与主视图“长对正”;
三视图的具体画法为:
主视图
俯视图
左视图
高
长
宽
宽
注:可见的轮廓线画成实线;不可见的轮廓线,画成虚线.
归纳:
4. 为表示圆柱、圆锥等的对称轴,规定在视图中加画点划线( )表示对称轴.
画出半球和圆锥的三视图.
半球
主视图
俯视图
左视图
圆锥
主视图
俯视图
左视图
·.
画出如图所示的支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.
解:下图是支架的三视图.
主视图
俯视图
左视图
五.已知较复杂几何体画三视图
提示:长对正,高平齐,宽相等,不可见的轮廓线,用虚线画出.
画出该几何体的三视图.
六.作几何组合体的三视图
分析:这是一个圆柱体的组合体,从不同角度看它时,会呈现不同的视图,为全面地反映立体图形的现状,画图时规定:
看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
主视图
左视图
俯视图
解:下图是组合体的三视图.
画出图中简单组合体的三视图:
主视图
左视图
俯视图
解:三视图如下:
画出图中的几何体的三视图.
解:如图所示:
下图是一根钢管的直观图,画出它的三视图.
解:钢管的三视图为:
主视图
俯视图
左视图
如图,分别根据三视图(1) (2)说出立体图形的名称.
图(2)
图(1)
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
七.根据三视图描述较简单物体的形状
解:(1)从三个方向看立体图形,视图都是矩形,可以想
象出:整体是 ,如图1所示.
(2)从正面、侧面看立体图形,视图都是等腰三角形; 从上面看,视图是圆;可以想象出:整体是 ,如图2所示.
长方体
圆锥
图1
图2
由三视图想象实物现状:
实物
实物
根据物体的三视图描述物体的形状.
分析:由主视图可知,物体的正面是正五边形;由俯视图可知,由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱 (中间的实线表示),可见到,另有两条棱 (虚线表示) 被遮挡;由左视图可知,物体左侧有两个面的视图是矩形,它们的交线是一条棱 (中间的实线表示),可见到.综合各视图可知,物体的形状是正五棱柱.
八.根据三视图描述较复杂物体的形状
主视图
俯视图
左视图
解:物体是正五棱柱形状的,如图所示.
【方法总结】由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面的局部形状,然后再综合起来考虑整体图形.
根据下列物体的三视图,填出几何体的名称:
(1) 如图①所示的几何体是__________;
(2) 如图②所示的几何体是_________.
图①
图②
六棱柱
圆台
左视图
左视图
俯视图
俯视图
主视图
主视图
主视图
左视图
俯视图
请根据下面提供的三视图,画出几何图形.
九.根据三视图画出几何体的图形
解:如下图所示:
(1) 主视图
左视图
俯视图
请根据下面提供的三视图,画出几何图形.
解:如下图所示:
请根据下面提供的三视图,画出几何图形.
(2) 主视图
左视图
俯视图
解:如下图所示:
(1) 一个几何体的主视图和左视图如图所示,请补画这个几
何体的俯视图.
(2) 一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.
左视图
主视图
俯视图
主视图
俯视图
左视图
解:如图所示:
解:如图所示:
(1)
根据三视图画出实物图形.
解:如下图所示:
(2)
解:如下图所示:
(3)
解:如下图所示:
分析:
1. 应先由三视图想象出
;
2. 画出物体的 .
密封罐的立体形状
展开图
某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位:mm).
十.利用三视图求物体的表面积
解:由三视图可知,密封罐的形状是正六棱柱.
50mm
50mm
密封罐的高为50mm,底面正六边形的直径为100mm,边长
为50mm,
100mm
如图,是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为
如图是一个几何体的三视图,试描绘出这个零件的形状,并求出此三视图所描述的几何体的表面积.
解:该几何体是一个组合体,上部是一个圆锥,下部是一个圆柱,该几何体的表面积为
π×22+2π×2×2+ ×4×4π=20 π.
主视图
左视图
俯视图
4
2
一个机器零件的三视图如图所示(单位:cm),这个机器零件是一个什么样的立体图形?它的体积是多少?
15
10
主视图
12
15
左视图
10
俯视图
解:长方体,其体积为10×12×15=1800(cm3).
十一.利用三视图求物体的体积
分析:由三视图可知该几何体是长方体.长方体的长、宽、高分别是10cm、12cm、15cm,然后利用长方体的体积公式即可.
12
已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为 .
解析:根据三视图得到圆锥的底面圆的直径为8,即底面圆的半径r为4,圆锥的高为3,
所以圆锥的母线长 ,
所以这个圆锥的侧面积是π×4×5=20π.
20π
3
8
主
视
图
左
视
图
俯
视
图
8
8
13
如图是一个几何体的三视图.根据图示,可计算出该几何体的侧面积为 .
104π
如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为 cm2.
2π
主视图
左视图
俯视图
如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
分析:由三视图可知该几何体是
由圆柱、长方体组合而成.分别
计算它们的表面积和体积,然后
相加即可.
主视图
左视图
俯视图
解:该图形上、下部分分别是圆柱、长方体,根据图中数据得:
体积为
25×30×40+102×32π
=(30000+3200π)(cm3).
表面积为
20π×32+(30×40+25×40+25×30)×2
=(5900+640π)(cm2),
30cm
20cm
25cm
32cm
40cm
如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图.
(1) 请写出构成这个几何体的正方体的个数为 ;
(2) 计算这个几何体的表面积为 .
5
20cm2
主视图
左视图
俯视图
某一空间图形的三视图如图所示,其中主视图是半径为1的半圆以及高为 1 的矩形;左视图是半径为1的四分之一圆以及高为1的矩形;俯视图是半径为1的圆,求此图形的体积 (参考公式:V球= πR 3).
主视图
左视图
俯视图
由三视图可得,下部圆柱的底面半径为1,高为1,则V圆柱=π,上部 球的半径为1,则 V球= ,故此几何体的体积为 .
主视图
左视图
俯视图
解:由已知可得该几何体是一个下部为圆柱,上部为 球的组合体.
1. 三种图形的转化:
2. 由三视图求立体图形的体积 (或面积) 的方法:
(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等;
(2) 根据已知数据,求出立体图形的体积 (或将立体图形展开成一个平面图形,求出展开图的面积).
三视图
立体图
展开图
