6.3余角、补角、对顶角 课后综合练 -2021-2022学年苏科版七年级数学上册(word版含解析)
文档属性
| 名称 | 6.3余角、补角、对顶角 课后综合练 -2021-2022学年苏科版七年级数学上册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 07:31:37 | ||
图片预览


文档简介
6.3余角、补角、对顶角【课后综合练】
-2021-2022学年七年级数学上册(苏科版)
一、选择题
1、已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
2、如图,将一副三角板按不同位置摆放,其中和互为余角的是
A.B. C.D.
3、如图,一副三角尺按不同的位置摆放,下列摆放方式中与一定相等的是( )
A.①② B.①③ C.②④ D.③④
4、如图各图中,与是对顶角的是
A.B. C.D.
5、如图,直线DE与BC相交于点O,∠1与∠2互余,∠COE=36°,则∠2的度数是( )
A.36° B.54° C.60° D.64°
(5题) (6题)
6、如图,直线和交于点,平分,若,则的度数为( )
A.75° B.80° C.100° D.120°
7、一个角的补角加上后,等于这个角的余角的3倍,则这个角是
A. B. C. D.
8、如果和互补,且,则下列式子中:①;②;③;
④.可以表示的余角的有
A.①② B.①②③ C.①②④ D.①②③④
9、如图,直线,相交于点,平分,且,则的度数是
A. B. C. D.
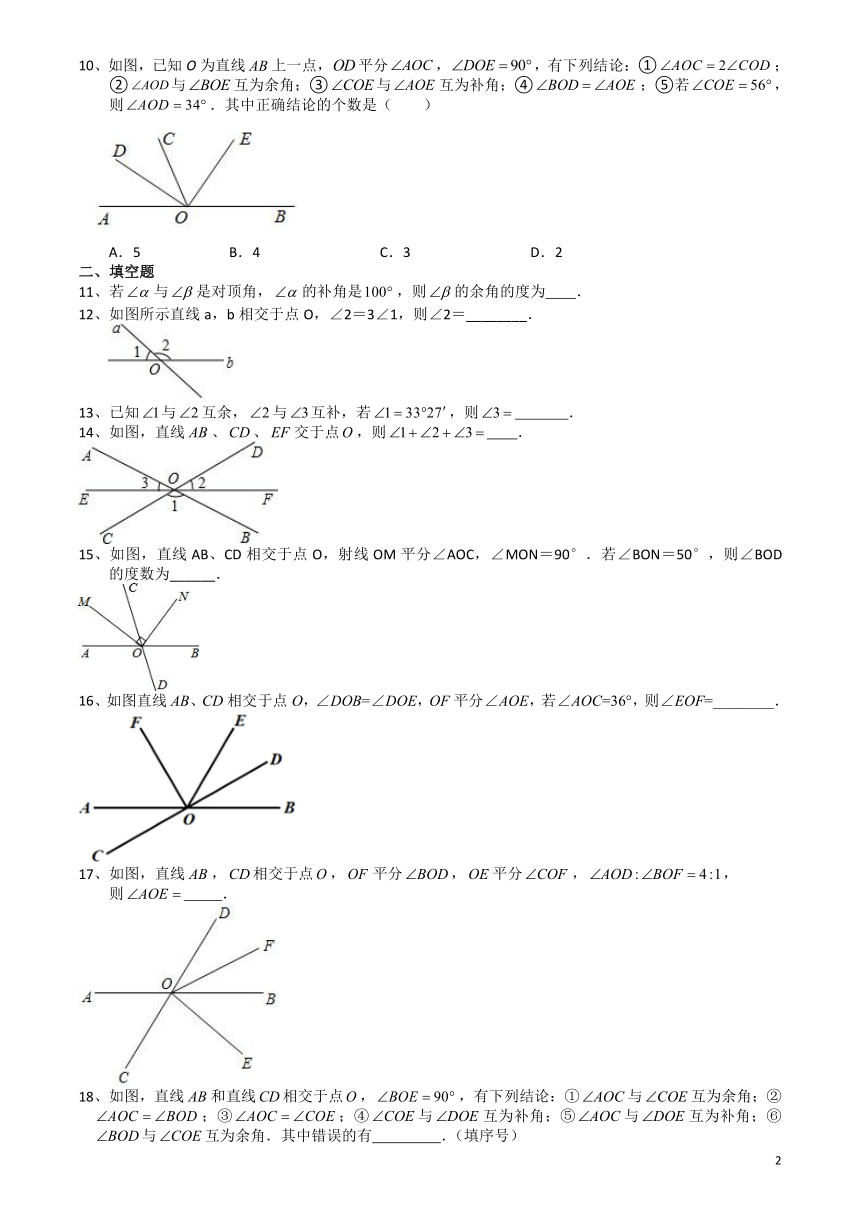
10、如图,已知O为直线上一点,平分,,有下列结论:①;②与互为余角;③与互为补角;④;⑤若,则.其中正确结论的个数是( )
A.5 B.4 C.3 D.2
二、填空题
11、若与是对顶角,的补角是,则的余角的度为 .
12、如图所示直线a,b相交于点O,∠2=3∠1,则∠2=________.
13、已知与互余,与互补,若,则 .
14、如图,直线、、交于点,则 .
15、如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠BON=50°,则∠BOD的度数为______.
16、如图直线AB、CD相交于点O,∠DOB=∠DOE,OF平分∠AOE,若∠AOC=36°,则∠EOF=________.
17、如图,直线,相交于点,平分,平分,,
则 .
18、如图,直线和直线相交于点,,有下列结论:①与互为余角;②;③;④与互为补角;⑤与互为补角;⑥与互为余角.其中错误的有 .(填序号)
三、解答题
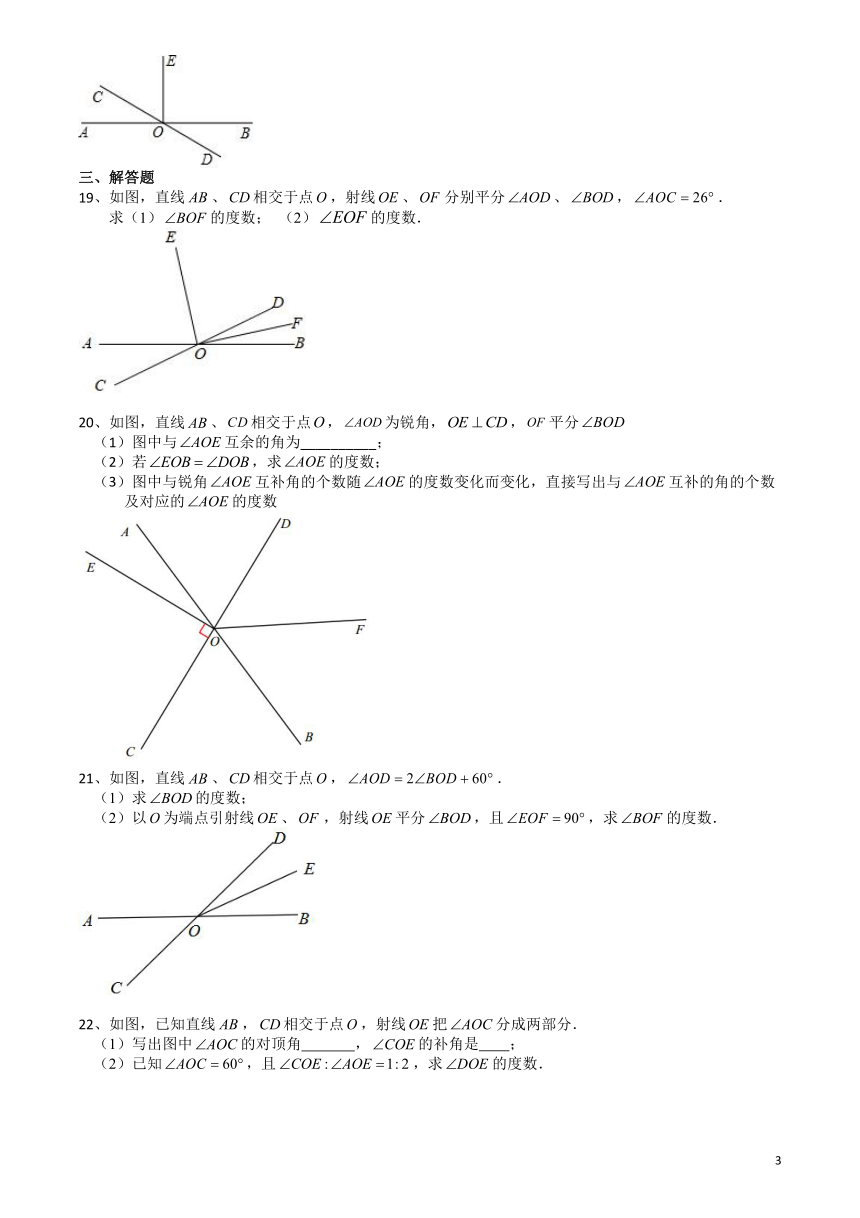
19、如图,直线、相交于点,射线、分别平分、,.
求(1)的度数; (2)的度数.
20、如图,直线、相交于点,为锐角,,平分
(1)图中与互余的角为__________;
(2)若,求的度数;
(3)图中与锐角互补角的个数随的度数变化而变化,直接写出与互补的角的个数及对应的的度数
21、如图,直线、相交于点,.
(1)求的度数;
(2)以为端点引射线、,射线平分,且,求的度数.
22、如图,已知直线,相交于点,射线把分成两部分.
(1)写出图中的对顶角 ,的补角是 ;
(2)已知,且,求的度数.
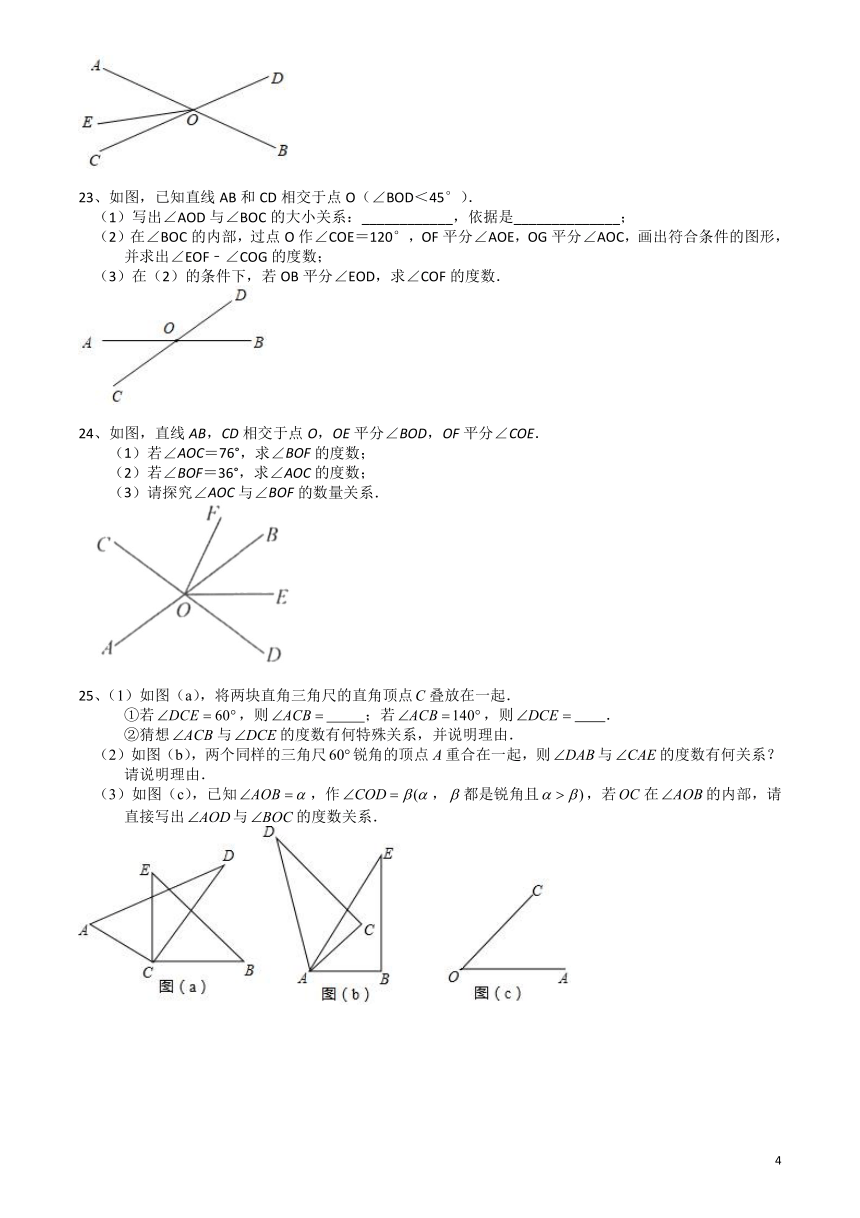
23、如图,已知直线AB和CD相交于点O(∠BOD<45°).
(1)写出∠AOD与∠BOC的大小关系:____________,依据是______________;
(2)在∠BOC的内部,过点O作∠COE=120°,OF平分∠AOE,OG平分∠AOC,画出符合条件的图形,并求出∠EOF﹣∠COG的度数;
(3)在(2)的条件下,若OB平分∠EOD,求∠COF的度数.
24、如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)请探究∠AOC与∠BOF的数量关系.
25、(1)如图(a),将两块直角三角尺的直角顶点叠放在一起.
①若,则 ;若,则 .
②猜想与的度数有何特殊关系,并说明理由.
(2)如图(b),两个同样的三角尺锐角的顶点重合在一起,则与的度数有何关系?请说明理由.
(3)如图(c),已知,作,都是锐角且,若在的内部,请直接写出与的度数关系.
6.3余角、补角、对顶角【课后综合练】
-2021-2022学年七年级数学上册(苏科版)(解析)
一、选择题
1、已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
【答案】B
【分析】
根据互为余角相加等于以及度分秒的进率计算即可.
【详解】
解:∵∠α=25°30′,
∴它的余角为,
故选:B.
2、如图,将一副三角板按不同位置摆放,其中和互为余角的是
A.B. C.D.
【分析】根据图形,结合互余的定义判断即可.
【解析】:、和互余,故本选项正确;
、和不互余,故本选项错误;
、和不互余,故本选项错误;
、和不互余,故本选项错误.
故选:.
3、如图,一副三角尺按不同的位置摆放,下列摆放方式中与一定相等的是( )
A.①② B.①③ C.②④ D.③④
【答案】B
【分析】
根据同角的余角相等,邻补角定义,等角的补角相等和平角的定义对各小题分析判断即可得解.
【详解】
解:图①,根据同角的余角相等,可得;
图②,,,∴;
图③,根据等角的补角相等,可得;
图④,,互余.
与一定相等的是图①和图③.
故选:B.
4、如图各图中,与是对顶角的是
A.B. C.D.
【分析】根据对顶角的定义判断即可.
【解析】根据两条直线相交,才能构成对顶角进行判断,
、、都不是由两条直线相交构成的图形,错误,
是由两条直线相交构成的图形,正确,
故选:.
5、如图,直线DE与BC相交于点O,∠1与∠2互余,∠COE=36°,则∠2的度数是( )
A.36° B.54° C.60° D.64°
【答案】B
【分析】根据对顶角相等求得∠1=∠COE=36°,再根据互余的两个角之和是90°求解∠2的度数即可.
【详解】解:∵∠COE=36°,∴∠1=∠COE=36°,
∵∠1与∠2互余,∴∠1+∠2=90°,∴∠2=90°﹣∠1=90°﹣36°=54°.故选:B.
6、如图,直线和交于点,平分,若,则的度数为( )
A.75° B.80° C.100° D.120°
【答案】A
【分析】根据对顶角相等可得:∠1=∠2=30°,从而得∠BOC=150°,进而即可求解.
【详解】解:∵∠1+∠2=60°,∠1=∠2,∴∠1=∠2=30°,∴∠BOC=180°-30°=150°,
∵平分,∴==×150°=75°.故选A.
7、一个角的补角加上后,等于这个角的余角的3倍,则这个角是
A. B. C. D.
【分析】可先设这个角为,则根据题意可得关于的方程,解即可.
【解析】:设这个角为,依题意,
得
解得.
故选:.
8、如果和互补,且,则下列式子中:①;②;③;
④.可以表示的余角的有
A.①② B.①②③ C.①②④ D.①②③④
【分析】互补即两角的和为,互余即两角的和为,根据这一条件判断即可.
【解析】:已知的余角为:,故①正确;
和互补,且,
,,
,
的余角为:,故②正确;
,
,
的余角为:,故④正确.
可以表示的余角的有:①②④.
故选:.
9、如图,直线,相交于点,平分,且,则的度数是
A. B. C. D.
【分析】根据角平分线的定义和对顶角的性质即可得到结论.
【解析】设,,
平分,
,
根据题意得,解得,
,
,
故选:.
10、如图,已知O为直线上一点,平分,,有下列结论:①;②与互为余角;③与互为补角;④;⑤若,则.其中正确结论的个数是( )
A.5 B.4 C.3 D.2
【答案】B
【分析】
由平分可判断①正确;由可判断②正确;由 ,,所以平分,根据与互补可判断③正确;由与互为余角不能说明可判断④不正确;由与互余可判断⑤正确,据此分析作答.
【详解】
解:∵O为直线上一点,平分,
∴,,故①正确;
∵,,,故②正确;
又,,即平分,,
,故③正确;
∵,,,,
∴不能说明,故④不正确;
, 当时,,故⑤正确.
综上, 正确,
故选:.
二、填空题
11、若与是对顶角,的补角是,则的余角的度为 .
【分析】根据补角定义可得的度数,再根据对顶角相等可得答案.
【解析】的补角为,
,
与是对顶角,
,
的余角的度为,
故答案为:.
12、如图所示直线a,b相交于点O,∠2=3∠1,则∠2=________.
解:依题意设∠1=x°,则∠2=3x°,
∵∠1+∠2=180°,
∴x°+3x°=180°,
解得x=45°,
∴∠2=135°.
故答案为:135°.
13、已知与互余,与互补,若,则 .
【分析】根据余角和补角的概念求出与的关系,把的值代入计算即可.
【解析】:与互余,
,
与互补,
,
,
,
故答案为:.
14、如图,直线、、交于点,则 .
【分析】先根据对顶角的性质得出,再根据邻补角的定义即可得出结论.
【解析】:与是对顶角,
,
,
.
故答案为:.
15、如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠BON=50°,则∠BOD的度数为______.
解:∵∠MON=90°.∠BON=50°,
∴∠AOM=90°﹣50°′=40°,
∵射线OM平分∠AOC,
∴∠AOC=40°×2=80°,
∴∠BOD=∠AOC=80°.
故答案为:80°.
16、如图直线AB、CD相交于点O,∠DOB=∠DOE,OF平分∠AOE,若∠AOC=36°,则∠EOF=________.
【答案】54°
【分析】
根据角平分线的定义可得∠EOF=∠AOF,根据平角的定义可得∠EOF+∠DOE=90°,根据对顶角相等可得∠BOD的度数,根据角的和差关系即可得答案.
【详解】
∵OF平分∠AOE,
∴∠EOF=∠AOF,
∵∠DOB=∠DOE,∠BOE+∠AOE=180°,
∴2∠EOF+2∠DOE=180°,
∴∠EOF+∠DOE=90°,
∵∠AOC=∠DOB=36°,
∴∠EOF=90°-∠DOE=90°-∠DOB=90°-36°=54°,
故答案为:54°
17、如图,直线,相交于点,平分,平分,,
则 .
【分析】根据角平分线的定义得出,,根据求出,根据邻补角互补求出,,求出,根据角平分线定义求出,再求出答案即可.
【解析】平分,
,,
,
,
,
,,
,
,
,
平分,
,
,
故答案为:.
18、如图,直线和直线相交于点,,有下列结论:①与互为余角;②;③;④与互为补角;⑤与互为补角;⑥与互为余角.其中错误的有 .(填序号)
【分析】根据对顶角相等、邻补角、垂直的意义、等量代换等知识,逐个进行判断即可.
【解析】:,
,
因此①不符合题意;
由对顶角相等可得②不符合题意;
,但与不一定相等,因此③符合题意;
,因此④不符合题意;
,但与不一定相等,因此⑤符合题意;
,且,因此⑥不符合题意;
故答案为:③⑤
三、解答题
19、如图,直线、相交于点,射线、分别平分、,.
求(1)的度数; (2)的度数.
【分析】(1)根据对顶角相等可得到的度数,再根据平分,即可得到的度数;
(2)根据角平分线的定义可得,,继而得到的度数.
【解析】:(1)直线、相交于点,,
.
平分,
.
(2).
平分,平分,
,,
,
即,
20、如图,直线、相交于点,为锐角,,平分
(1)图中与互余的角为__________;
(2)若,求的度数;
(3)图中与锐角互补角的个数随的度数变化而变化,直接写出与互补的角的个数及对应的的度数
【答案】(1)、;(2);(3)见解析.
【分析】(1)根据余角的定义可解答;(2)根据补角的定义列方程可解答;
(3)设出∠AOE的度数,依次表达图中的补角,可解.
【详解】(1)由题意可得于∠AOE互余的角为:、
(2)设.∵,∴,.
∵,∴.又∵,∴,即.
∴.
(3)设∠AOE=α,且0°<α<90°由(1)可知,∠AOD=∠BOC=90°-α,∠BOE=180°-α,
∴∠BOD=180°-∠AOD=180°-(90°-α)=90°+α,
∵OF平分∠BOD,∴∠BOF=∠DOF=45°+,∴∠AOF=∠AOD+∠DOF=90°-α+45°+=135°-,
∠EOF=∠AOF+∠AOE=135°+,∠COF=∠BOC+∠BOF=90°-α+45°+=135°-=∠AOF,
①当∠AOF+∠AOE=180°时,即135°-+α=180°,解得α=90°,不符合题意;
②当∠EOF+∠AOE=180°时,即135°++α=180°,解得α=30°,符合题意;
③当∠BOD+∠AOE=180°时,即90°+α+α=180°,解得α=45°,符合题意;
综上可知,当锐角时,互补角有2个,为、.
当锐角时,互补角有3个,为、、.
当锐角不等于和时,互补角有1个,为.
21、如图,直线、相交于点,.
(1)求的度数;
(2)以为端点引射线、,射线平分,且,求的度数.
【分析】(1)根据邻补角,可得关于的方程,根据解方程,可得答案;
(2)根据角平分线的性质,可得的度数,根据角的和差,可得的度数.
【解析】:(1)由邻补角互补,得,
又,
,
解得;
(2)如图:
由射线平分,得
,
由角的和差,得
,
.
的度数为或
22、如图,已知直线,相交于点,射线把分成两部分.
(1)写出图中的对顶角 ,的补角是 ;
(2)已知,且,求的度数.
【分析】(1)分析图形,根据对顶角和补角的定义可以求出答案;
(2)先设求得和的度数,再根据邻补角的定义求得的度数,然后将与的度数相加即可.
【解析】:(1)由图形可知,的对顶角是,的邻角是;
(2)设,则,
,
,
解得,
即,,
,
,
.
23、如图,已知直线AB和CD相交于点O(∠BOD<45°).
(1)写出∠AOD与∠BOC的大小关系:____________,依据是______________;
(2)在∠BOC的内部,过点O作∠COE=120°,OF平分∠AOE,OG平分∠AOC,画出符合条件的图形,并求出∠EOF﹣∠COG的度数;
(3)在(2)的条件下,若OB平分∠EOD,求∠COF的度数.
解:(1)根据对顶角相等可得,∠AOD=∠BOC,
理由:对顶角相等, 故答案为:∠AOD=∠BOC,对顶角相等;
(2)如图,∵OF平分∠AOE,∴∠EOF=∠AOF=∠AOE,
又∵OG平分∠AOC,∴∠COG=∠AOG=∠AOC,
∴∠EOF﹣∠COG=∠AOE﹣∠AOC=(∠AOE﹣∠AOC)=∠COE=×120°=60°;
(3)∵∠COE=120°,∴∠DOE=180°﹣120°=60°,
又∵OB平分∠DOE,∴∠DOB=∠BOE=∠DOE=30°,∴∠AOC=∠BOD=30°,
∵∠COE=120°,∴∠AOE=∠AOC+∠COE=150°,
又∵OF平分∠AOE,∴∠AOF=∠EOF=∠AOE=75°
∴∠COF=∠AOF﹣∠AOC=75°﹣30°=45°.
24、如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)请探究∠AOC与∠BOF的数量关系.
【答案】(1)33°;(2)72°;(3)
【分析】(1)根据对顶角相等求得的度数,然后根据角的平分线的定义求得的度数,则即可求得,再根据角平分线的定义求得,最后根据求解.
(2)利用角平分线定义得出,,进而表示出各角求出答案.
(3)由(1)知,计算即可求解.
【详解】解:(1),又平分,
.,
平分,,.
(2)平分,平分,,,
设,则,故,,
则,解得:,故.
(3)由(1)知
,即.
25、(1)如图(a),将两块直角三角尺的直角顶点叠放在一起.
①若,则 ;若,则 .
②猜想与的度数有何特殊关系,并说明理由.
(2)如图(b),两个同样的三角尺锐角的顶点重合在一起,则与的度数有何关系?请说明理由.
(3)如图(c),已知,作,都是锐角且,若在的内部,请直接写出与的度数关系.
【分析】(1)①先求出,再代入求出即可;先求出,再代入求出即可;
②先计算:,再加上可得结果;
(2)先计算,再加上可得结果;
(3)分情况讨论:①在上方;在内部;③在内部;④在下方.
【解析】:(1)①若
,,
,
若
,
,.
故答案为:;;
②
;
(2).
;
;
(3)①在上方时,如图
②在内部,如图
;
③在内部,如图
;
④在下方,如图
.
综上所述,或或.
-2021-2022学年七年级数学上册(苏科版)
一、选择题
1、已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
2、如图,将一副三角板按不同位置摆放,其中和互为余角的是
A.B. C.D.
3、如图,一副三角尺按不同的位置摆放,下列摆放方式中与一定相等的是( )
A.①② B.①③ C.②④ D.③④
4、如图各图中,与是对顶角的是
A.B. C.D.
5、如图,直线DE与BC相交于点O,∠1与∠2互余,∠COE=36°,则∠2的度数是( )
A.36° B.54° C.60° D.64°
(5题) (6题)
6、如图,直线和交于点,平分,若,则的度数为( )
A.75° B.80° C.100° D.120°
7、一个角的补角加上后,等于这个角的余角的3倍,则这个角是
A. B. C. D.
8、如果和互补,且,则下列式子中:①;②;③;
④.可以表示的余角的有
A.①② B.①②③ C.①②④ D.①②③④
9、如图,直线,相交于点,平分,且,则的度数是
A. B. C. D.
10、如图,已知O为直线上一点,平分,,有下列结论:①;②与互为余角;③与互为补角;④;⑤若,则.其中正确结论的个数是( )
A.5 B.4 C.3 D.2
二、填空题
11、若与是对顶角,的补角是,则的余角的度为 .
12、如图所示直线a,b相交于点O,∠2=3∠1,则∠2=________.
13、已知与互余,与互补,若,则 .
14、如图,直线、、交于点,则 .
15、如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠BON=50°,则∠BOD的度数为______.
16、如图直线AB、CD相交于点O,∠DOB=∠DOE,OF平分∠AOE,若∠AOC=36°,则∠EOF=________.
17、如图,直线,相交于点,平分,平分,,
则 .
18、如图,直线和直线相交于点,,有下列结论:①与互为余角;②;③;④与互为补角;⑤与互为补角;⑥与互为余角.其中错误的有 .(填序号)
三、解答题
19、如图,直线、相交于点,射线、分别平分、,.
求(1)的度数; (2)的度数.
20、如图,直线、相交于点,为锐角,,平分
(1)图中与互余的角为__________;
(2)若,求的度数;
(3)图中与锐角互补角的个数随的度数变化而变化,直接写出与互补的角的个数及对应的的度数
21、如图,直线、相交于点,.
(1)求的度数;
(2)以为端点引射线、,射线平分,且,求的度数.
22、如图,已知直线,相交于点,射线把分成两部分.
(1)写出图中的对顶角 ,的补角是 ;
(2)已知,且,求的度数.
23、如图,已知直线AB和CD相交于点O(∠BOD<45°).
(1)写出∠AOD与∠BOC的大小关系:____________,依据是______________;
(2)在∠BOC的内部,过点O作∠COE=120°,OF平分∠AOE,OG平分∠AOC,画出符合条件的图形,并求出∠EOF﹣∠COG的度数;
(3)在(2)的条件下,若OB平分∠EOD,求∠COF的度数.
24、如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)请探究∠AOC与∠BOF的数量关系.
25、(1)如图(a),将两块直角三角尺的直角顶点叠放在一起.
①若,则 ;若,则 .
②猜想与的度数有何特殊关系,并说明理由.
(2)如图(b),两个同样的三角尺锐角的顶点重合在一起,则与的度数有何关系?请说明理由.
(3)如图(c),已知,作,都是锐角且,若在的内部,请直接写出与的度数关系.
6.3余角、补角、对顶角【课后综合练】
-2021-2022学年七年级数学上册(苏科版)(解析)
一、选择题
1、已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
【答案】B
【分析】
根据互为余角相加等于以及度分秒的进率计算即可.
【详解】
解:∵∠α=25°30′,
∴它的余角为,
故选:B.
2、如图,将一副三角板按不同位置摆放,其中和互为余角的是
A.B. C.D.
【分析】根据图形,结合互余的定义判断即可.
【解析】:、和互余,故本选项正确;
、和不互余,故本选项错误;
、和不互余,故本选项错误;
、和不互余,故本选项错误.
故选:.
3、如图,一副三角尺按不同的位置摆放,下列摆放方式中与一定相等的是( )
A.①② B.①③ C.②④ D.③④
【答案】B
【分析】
根据同角的余角相等,邻补角定义,等角的补角相等和平角的定义对各小题分析判断即可得解.
【详解】
解:图①,根据同角的余角相等,可得;
图②,,,∴;
图③,根据等角的补角相等,可得;
图④,,互余.
与一定相等的是图①和图③.
故选:B.
4、如图各图中,与是对顶角的是
A.B. C.D.
【分析】根据对顶角的定义判断即可.
【解析】根据两条直线相交,才能构成对顶角进行判断,
、、都不是由两条直线相交构成的图形,错误,
是由两条直线相交构成的图形,正确,
故选:.
5、如图,直线DE与BC相交于点O,∠1与∠2互余,∠COE=36°,则∠2的度数是( )
A.36° B.54° C.60° D.64°
【答案】B
【分析】根据对顶角相等求得∠1=∠COE=36°,再根据互余的两个角之和是90°求解∠2的度数即可.
【详解】解:∵∠COE=36°,∴∠1=∠COE=36°,
∵∠1与∠2互余,∴∠1+∠2=90°,∴∠2=90°﹣∠1=90°﹣36°=54°.故选:B.
6、如图,直线和交于点,平分,若,则的度数为( )
A.75° B.80° C.100° D.120°
【答案】A
【分析】根据对顶角相等可得:∠1=∠2=30°,从而得∠BOC=150°,进而即可求解.
【详解】解:∵∠1+∠2=60°,∠1=∠2,∴∠1=∠2=30°,∴∠BOC=180°-30°=150°,
∵平分,∴==×150°=75°.故选A.
7、一个角的补角加上后,等于这个角的余角的3倍,则这个角是
A. B. C. D.
【分析】可先设这个角为,则根据题意可得关于的方程,解即可.
【解析】:设这个角为,依题意,
得
解得.
故选:.
8、如果和互补,且,则下列式子中:①;②;③;
④.可以表示的余角的有
A.①② B.①②③ C.①②④ D.①②③④
【分析】互补即两角的和为,互余即两角的和为,根据这一条件判断即可.
【解析】:已知的余角为:,故①正确;
和互补,且,
,,
,
的余角为:,故②正确;
,
,
的余角为:,故④正确.
可以表示的余角的有:①②④.
故选:.
9、如图,直线,相交于点,平分,且,则的度数是
A. B. C. D.
【分析】根据角平分线的定义和对顶角的性质即可得到结论.
【解析】设,,
平分,
,
根据题意得,解得,
,
,
故选:.
10、如图,已知O为直线上一点,平分,,有下列结论:①;②与互为余角;③与互为补角;④;⑤若,则.其中正确结论的个数是( )
A.5 B.4 C.3 D.2
【答案】B
【分析】
由平分可判断①正确;由可判断②正确;由 ,,所以平分,根据与互补可判断③正确;由与互为余角不能说明可判断④不正确;由与互余可判断⑤正确,据此分析作答.
【详解】
解:∵O为直线上一点,平分,
∴,,故①正确;
∵,,,故②正确;
又,,即平分,,
,故③正确;
∵,,,,
∴不能说明,故④不正确;
, 当时,,故⑤正确.
综上, 正确,
故选:.
二、填空题
11、若与是对顶角,的补角是,则的余角的度为 .
【分析】根据补角定义可得的度数,再根据对顶角相等可得答案.
【解析】的补角为,
,
与是对顶角,
,
的余角的度为,
故答案为:.
12、如图所示直线a,b相交于点O,∠2=3∠1,则∠2=________.
解:依题意设∠1=x°,则∠2=3x°,
∵∠1+∠2=180°,
∴x°+3x°=180°,
解得x=45°,
∴∠2=135°.
故答案为:135°.
13、已知与互余,与互补,若,则 .
【分析】根据余角和补角的概念求出与的关系,把的值代入计算即可.
【解析】:与互余,
,
与互补,
,
,
,
故答案为:.
14、如图,直线、、交于点,则 .
【分析】先根据对顶角的性质得出,再根据邻补角的定义即可得出结论.
【解析】:与是对顶角,
,
,
.
故答案为:.
15、如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠BON=50°,则∠BOD的度数为______.
解:∵∠MON=90°.∠BON=50°,
∴∠AOM=90°﹣50°′=40°,
∵射线OM平分∠AOC,
∴∠AOC=40°×2=80°,
∴∠BOD=∠AOC=80°.
故答案为:80°.
16、如图直线AB、CD相交于点O,∠DOB=∠DOE,OF平分∠AOE,若∠AOC=36°,则∠EOF=________.
【答案】54°
【分析】
根据角平分线的定义可得∠EOF=∠AOF,根据平角的定义可得∠EOF+∠DOE=90°,根据对顶角相等可得∠BOD的度数,根据角的和差关系即可得答案.
【详解】
∵OF平分∠AOE,
∴∠EOF=∠AOF,
∵∠DOB=∠DOE,∠BOE+∠AOE=180°,
∴2∠EOF+2∠DOE=180°,
∴∠EOF+∠DOE=90°,
∵∠AOC=∠DOB=36°,
∴∠EOF=90°-∠DOE=90°-∠DOB=90°-36°=54°,
故答案为:54°
17、如图,直线,相交于点,平分,平分,,
则 .
【分析】根据角平分线的定义得出,,根据求出,根据邻补角互补求出,,求出,根据角平分线定义求出,再求出答案即可.
【解析】平分,
,,
,
,
,
,,
,
,
,
平分,
,
,
故答案为:.
18、如图,直线和直线相交于点,,有下列结论:①与互为余角;②;③;④与互为补角;⑤与互为补角;⑥与互为余角.其中错误的有 .(填序号)
【分析】根据对顶角相等、邻补角、垂直的意义、等量代换等知识,逐个进行判断即可.
【解析】:,
,
因此①不符合题意;
由对顶角相等可得②不符合题意;
,但与不一定相等,因此③符合题意;
,因此④不符合题意;
,但与不一定相等,因此⑤符合题意;
,且,因此⑥不符合题意;
故答案为:③⑤
三、解答题
19、如图,直线、相交于点,射线、分别平分、,.
求(1)的度数; (2)的度数.
【分析】(1)根据对顶角相等可得到的度数,再根据平分,即可得到的度数;
(2)根据角平分线的定义可得,,继而得到的度数.
【解析】:(1)直线、相交于点,,
.
平分,
.
(2).
平分,平分,
,,
,
即,
20、如图,直线、相交于点,为锐角,,平分
(1)图中与互余的角为__________;
(2)若,求的度数;
(3)图中与锐角互补角的个数随的度数变化而变化,直接写出与互补的角的个数及对应的的度数
【答案】(1)、;(2);(3)见解析.
【分析】(1)根据余角的定义可解答;(2)根据补角的定义列方程可解答;
(3)设出∠AOE的度数,依次表达图中的补角,可解.
【详解】(1)由题意可得于∠AOE互余的角为:、
(2)设.∵,∴,.
∵,∴.又∵,∴,即.
∴.
(3)设∠AOE=α,且0°<α<90°由(1)可知,∠AOD=∠BOC=90°-α,∠BOE=180°-α,
∴∠BOD=180°-∠AOD=180°-(90°-α)=90°+α,
∵OF平分∠BOD,∴∠BOF=∠DOF=45°+,∴∠AOF=∠AOD+∠DOF=90°-α+45°+=135°-,
∠EOF=∠AOF+∠AOE=135°+,∠COF=∠BOC+∠BOF=90°-α+45°+=135°-=∠AOF,
①当∠AOF+∠AOE=180°时,即135°-+α=180°,解得α=90°,不符合题意;
②当∠EOF+∠AOE=180°时,即135°++α=180°,解得α=30°,符合题意;
③当∠BOD+∠AOE=180°时,即90°+α+α=180°,解得α=45°,符合题意;
综上可知,当锐角时,互补角有2个,为、.
当锐角时,互补角有3个,为、、.
当锐角不等于和时,互补角有1个,为.
21、如图,直线、相交于点,.
(1)求的度数;
(2)以为端点引射线、,射线平分,且,求的度数.
【分析】(1)根据邻补角,可得关于的方程,根据解方程,可得答案;
(2)根据角平分线的性质,可得的度数,根据角的和差,可得的度数.
【解析】:(1)由邻补角互补,得,
又,
,
解得;
(2)如图:
由射线平分,得
,
由角的和差,得
,
.
的度数为或
22、如图,已知直线,相交于点,射线把分成两部分.
(1)写出图中的对顶角 ,的补角是 ;
(2)已知,且,求的度数.
【分析】(1)分析图形,根据对顶角和补角的定义可以求出答案;
(2)先设求得和的度数,再根据邻补角的定义求得的度数,然后将与的度数相加即可.
【解析】:(1)由图形可知,的对顶角是,的邻角是;
(2)设,则,
,
,
解得,
即,,
,
,
.
23、如图,已知直线AB和CD相交于点O(∠BOD<45°).
(1)写出∠AOD与∠BOC的大小关系:____________,依据是______________;
(2)在∠BOC的内部,过点O作∠COE=120°,OF平分∠AOE,OG平分∠AOC,画出符合条件的图形,并求出∠EOF﹣∠COG的度数;
(3)在(2)的条件下,若OB平分∠EOD,求∠COF的度数.
解:(1)根据对顶角相等可得,∠AOD=∠BOC,
理由:对顶角相等, 故答案为:∠AOD=∠BOC,对顶角相等;
(2)如图,∵OF平分∠AOE,∴∠EOF=∠AOF=∠AOE,
又∵OG平分∠AOC,∴∠COG=∠AOG=∠AOC,
∴∠EOF﹣∠COG=∠AOE﹣∠AOC=(∠AOE﹣∠AOC)=∠COE=×120°=60°;
(3)∵∠COE=120°,∴∠DOE=180°﹣120°=60°,
又∵OB平分∠DOE,∴∠DOB=∠BOE=∠DOE=30°,∴∠AOC=∠BOD=30°,
∵∠COE=120°,∴∠AOE=∠AOC+∠COE=150°,
又∵OF平分∠AOE,∴∠AOF=∠EOF=∠AOE=75°
∴∠COF=∠AOF﹣∠AOC=75°﹣30°=45°.
24、如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)请探究∠AOC与∠BOF的数量关系.
【答案】(1)33°;(2)72°;(3)
【分析】(1)根据对顶角相等求得的度数,然后根据角的平分线的定义求得的度数,则即可求得,再根据角平分线的定义求得,最后根据求解.
(2)利用角平分线定义得出,,进而表示出各角求出答案.
(3)由(1)知,计算即可求解.
【详解】解:(1),又平分,
.,
平分,,.
(2)平分,平分,,,
设,则,故,,
则,解得:,故.
(3)由(1)知
,即.
25、(1)如图(a),将两块直角三角尺的直角顶点叠放在一起.
①若,则 ;若,则 .
②猜想与的度数有何特殊关系,并说明理由.
(2)如图(b),两个同样的三角尺锐角的顶点重合在一起,则与的度数有何关系?请说明理由.
(3)如图(c),已知,作,都是锐角且,若在的内部,请直接写出与的度数关系.
【分析】(1)①先求出,再代入求出即可;先求出,再代入求出即可;
②先计算:,再加上可得结果;
(2)先计算,再加上可得结果;
(3)分情况讨论:①在上方;在内部;③在内部;④在下方.
【解析】:(1)①若
,,
,
若
,
,.
故答案为:;;
②
;
(2).
;
;
(3)①在上方时,如图
②在内部,如图
;
③在内部,如图
;
④在下方,如图
.
综上所述,或或.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
