7.5三角形的内角和 同步达标测评 2021-2022学年北师大版八年级数学上册(word版含解析)
文档属性
| 名称 | 7.5三角形的内角和 同步达标测评 2021-2022学年北师大版八年级数学上册(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 447.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 07:34:40 | ||
图片预览




文档简介
2021-2022学年北师大版八年级数学上册《7.5三角形的内角和》同步达标测评(附答案)
一.选择题(共15小题满分45分)
1.BP是∠ABC的平分线,CP是∠ACB的邻补角的平分线,∠ABP=20°,∠ACP=50°,则∠P=( )
A.30° B.40° C.50° D.60°
2.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=70°,则∠BOC的度数为( )
A.125° B.130° C.135° D.140°
3.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若∠DBC=54°,则∠A的度数为( )
A.36° B.44° C.27° D.54°
4.如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,得∠A1,∠A1BC与∠A1CD的平分线相交于点A2,得∠A2,…,∠A3BC与∠A3CD的平分线相交于点A4,得∠A4,则∠A4的度数为( )
A.5° B.4° C.8° D.16°
5.如图,点A、C在∠FBD的两条边BF、BD上,BE平分∠FBD,CE平分∠ACD,连接AE,若∠BEC=35°,则∠FAE的度数为( )
A.35° B.45° C.55° D.65°
6.如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=120°,则∠1+∠2的度数为( )
A.90° B.100° C.110° D.120°
7.如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠ADE的度数为( )
A.100° B.110° C.120° D.130°
8.已知:如图所示,将△ABC的∠C沿DE折叠,点C落在点C'处,若设∠C=α,∠AEC′=β,∠BDC'=γ,则下列关系成立的是( )
A.2α=β+γ B.α=β+γ C.α+β+γ=180° D.α+β=2γ
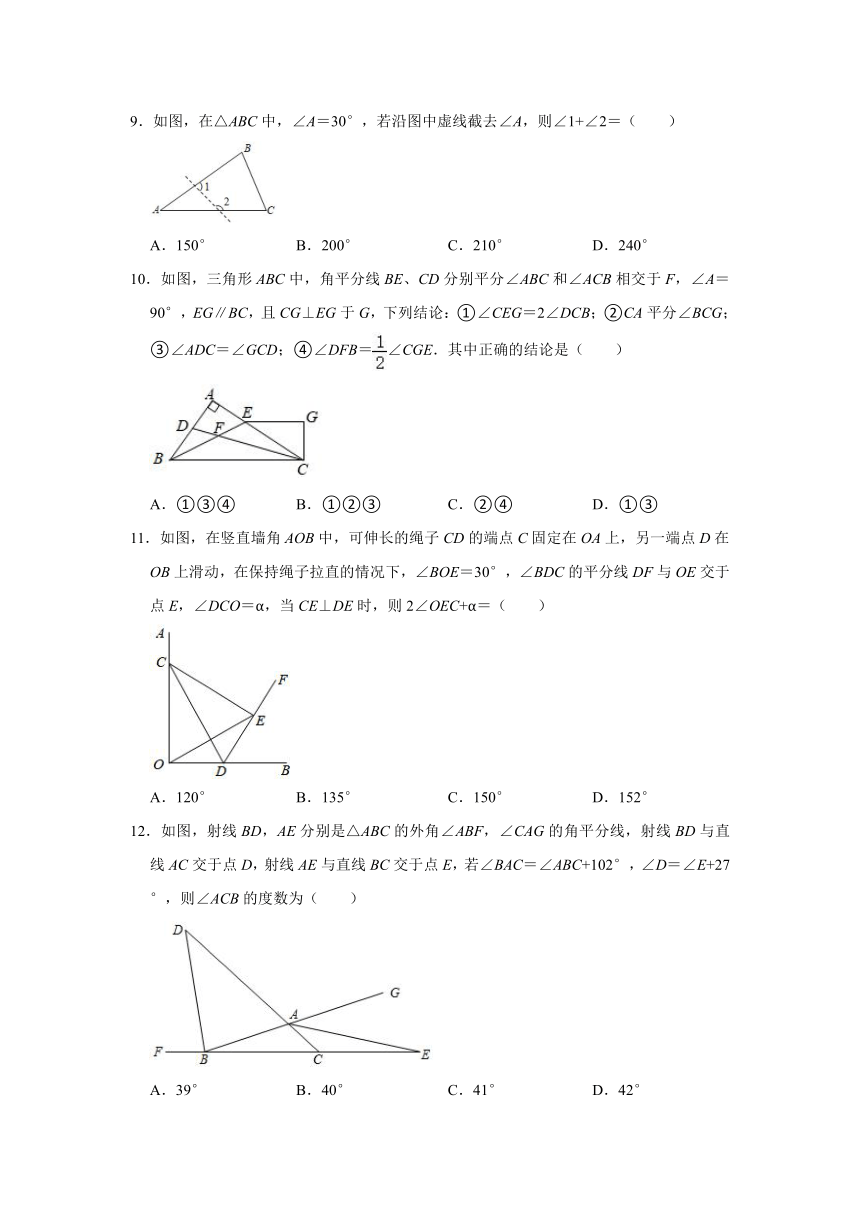
9.如图,在△ABC中,∠A=30°,若沿图中虚线截去∠A,则∠1+∠2=( )
A.150° B.200° C.210° D.240°
10.如图,三角形ABC中,角平分线BE、CD分别平分∠ABC和∠ACB相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=∠CGE.其中正确的结论是( )
A.①③④ B.①②③ C.②④ D.①③
11.如图,在竖直墙角AOB中,可伸长的绳子CD的端点C固定在OA上,另一端点D在OB上滑动,在保持绳子拉直的情况下,∠BOE=30°,∠BDC的平分线DF与OE交于点E,∠DCO=α,当CE⊥DE时,则2∠OEC+α=( )
A.120° B.135° C.150° D.152°
12.如图,射线BD,AE分别是△ABC的外角∠ABF,∠CAG的角平分线,射线BD与直线AC交于点D,射线AE与直线BC交于点E,若∠BAC=∠ABC+102°,∠D=∠E+27°,则∠ACB的度数为( )
A.39° B.40° C.41° D.42°
13.如图,在△ABC中,∠B=28°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.42° B.46° C.52° D.56°
14.如图,在△ABC中,AE平分∠BAC,AD⊥BC于点D.∠ABD的角平分线BF所在直线与射线AE相交于点G,若∠ABC=3∠C,且∠G=20°,则∠DFB的度数为( )
A.50° B.55° C.60° D.65°
15.如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
A.50° B.55° C.70° D.80°
二.填空题(共6小题满分30分)
16.如图,∠MAN=100°,点B,C是射线AM.AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小为 .
17.如图,在△ABC中,∠F=16°,BD、CD分别平分∠ABC,∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC,∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠A= .
18.如图,△ABC的两条外角平分线AP,CP相交于点P,PH⊥AC于点H.若∠ABC=∠ACB=60°,则下列结论:①∠ABP=30°;②∠APC=60°;③PA∥BC,其中正确的结论有 .(填序号)
19.如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,…,若∠A=α,则∠A2021为 .
20.如图,将△ABC沿DE、DF翻折,使顶点B、C都落于点G处,且线段BD、CD翻折后重合于DG,若∠AEG+∠AFG=54°,则∠A= 度.
21.如图,在△ABC中,BD平分∠ABC,CE平分∠ACB,BD与CE交于点M.若MN⊥BC于N,∠A=60°,则∠1﹣∠2= 度.
三.解答题(共4小题满分45分)
22.如图,在△ABC中,点D是AC延长线上的一点,过点D作DE∥BC,DF平分∠ADE,BF平分∠ABC.设∠A=n°,求∠F的度数(用含n的式子表示).
23.已知在△ABC中,图1,图2,图3中的△ABC的内角平分线或外角平分线交于点O.
(1)如图1,点O是△ABC的两个内角平分线的交点,猜想∠O与∠A之间的数量关系,并加以证明.
(2)请直接写出结果.如图2,若∠A=60°,△ABC的内角平分线与外角平分线交于点O,则∠O= ;如图3,若∠A=60°,△ABC的两个外角平分线交于点O,则∠O= .
24.嘉琪在学习过程中,对教材的一个有趣的问题做如下探究:
【习题回顾】
已知:如图1,在△ABC中,∠A=40°,角平分线BO、CO交于点O.求∠BOC的度数.
(1)请直接写出∠BOC= .
【变式思考】
(2)若∠A=α,请猜想∠BOC与α的关系,并说明理由;
【拓展延伸】
(3)已知:如图2,在△ABC中,角平分线BO、CO交于点O,OD⊥OB,交边BC于点D,作∠ABE的平分线交CO的延长线于点F.若∠F=β,猜想∠BAC与β的关系,并说明理由.
25.∠MOQ=90°,点A,B分别在射线OM、OQ上运动(不与点O重合).
(1)如图1,AI平分∠BAO,BI平分∠ABO,若∠BAO=40°,求∠AIB的度数.
(2)如图2,AI平分∠BAO,BC平分∠ABM,BC的反向延长线交AI于点D.
①若∠BAO=40°,则∠ADB= °;
②点A、B在运动的过程中,∠ADB是否发生变化,若不变,试求∠ADB的度数;若变化,请说明变化规律.
参考答案
一.选择题(共15小题,满分45分)
1.解:∵CP是∠ACM的角平分线,∠ACP=90°,
∴∠ACM=2∠ACP=100°,
∴∠ACB=80°,
∵BP是∠ABC的角平分线,∠ABP=20°,
∴∠CBP=∠ABP=20°,
∴∠P=180°﹣∠CBP﹣∠ACB﹣∠ACP
=180°﹣20°﹣80°﹣50°
=30°,
故选:A.
2.解:∵∠A=70°,
∴∠ABC+∠ACB=180°﹣∠A=110°,
∵BO、CO分别是∠ABC、∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°.
故选:A.
3.解:∵BD⊥CD,
∴∠D=90°.
∵∠DBC=54°,
∴∠DCB=90°﹣54°=36°.
∵CD平分∠ACB,
∴∠ACB=72°.
∵∠A=∠ABD,∠A+∠ABC+∠ACB=180°,
∴∠A+∠A+54°+72°=180°.
∴∠A=27°.
故选:C.
4.解:∵∠ABC与∠ACD的平分线交于点A1,
∴∠A1BC=,,
由三角形的外角性质得,
∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∴,
=,
∴∠A1==32°,
同理∠A4==4°,
故选:B.
5.解:∵BE平分∠FBD,CE平分∠ACD,
∴∠ABC=2∠EBD,∠ACD=2∠ECD,AE平分∠FAC,
∵∠ACD=∠ABC+∠BAC,∠ECD=∠EBC+∠BEC,
∴2∠ECD=2∠EBD+∠BAC,2∠ECD=2∠EBD+2∠BEC,
∴∠BAC=2∠BEC,
∵∠BEC=35°,
∴∠BAC=2×35°=70°,
∵∠BAC+∠FAC=180°,
∴∠FAC=180°﹣70°=110°,
∵AE平分∠FAC,
∴∠FAE=∠FAC=55°.
故选:C.
6.解:如图,连接AA',
∵A'B平分∠ABC,A'C平分∠ACB,
∴∠A'BC=∠ABC,∠A'CB=∠ACB,
∵∠BA'C=120°,
∴∠A'BC+∠A'CB=180°﹣120°=60°,
∴∠ABC+∠ACB=120°,
∴∠BAC=180°﹣120°=60°,
∵沿DE折叠,
∴∠DAA'=∠DA'A,∠EAA'=∠EA'A,
∵∠1=∠DAA'+∠DA'A=2∠DAA',∠2=∠EAA'+∠EA'A=2∠EAA',
∴∠1+∠2=2∠DAA'+2∠EAA'=2∠BAC=2×60°=120°,
故选:D.
7.解:∵∠B=40°,∠C=30°,
∴∠BAC=110°,
由折叠的性质得,∠E=∠C=30°,∠EAD=∠CAD,∠ADE=∠ADC,
∵DE∥AB,
∴∠BAE=∠E=30°,
∴∠CAD=40°,
∴∠ADE=∠ADC=180°﹣∠CAD﹣∠C=110°,
故选:B.
8.解:由折叠的性质知:∠C=∠C′=α.
∵∠AEC′+∠CEC′=180°,∠BDC′+∠CDC′=180°,
∴β=180°﹣∠CEC′,γ=180°﹣∠CDC′.
∴β+γ=360°﹣∠CEC′﹣∠CDC′.
∵∠C+∠CEC′+CDC′+∠C′=360°,
∴2α=360°﹣∠CEC′﹣CDC′.
∴β+γ=2α.
故选:A.
9.解:如图:∠1+∠3=180°,∠2+∠4=180°,
∴∠1+∠2+∠3+∠4=360°,
∵∠A+∠3+∠4=180°,∠A=30°,
∴∠3+∠4=150°,
∴∠1+∠2=210°.
故选:C.
10.解:①∵EG∥BC,
∴∠CEG=∠ACB,
又∵CD是△ABC的角平分线,
∴∠CEG=∠ACB=2∠DCB,故①正确;
②∵∠CEG=∠ACB,而∠GEC与∠GCE不一定相等,
∴CA不一定平分∠BCG,故②错误;
③∵∠A=90°,
∴∠ADC+∠ACD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC+∠BCD=90°.
∵EG∥BC,且CG⊥EG,
∴∠GCB=90°,即∠GCD+∠BCD=90°,
∴∠ADC=∠GCD,故③正确;
④∵∠ABC+∠ACB=90°,
∵CD平分∠ACB,BE平分∠ABC,
∴∠EBC=∠ABC,∠DCB=∠ACB,
∴∠DFB=∠EBC+∠DCB=(∠ABC+∠ACB)=45°,
∵∠CGE=90°,
∴∠DFB=∠CGE,故④正确.
综上所述,正确的有:①③④.
故选:A.
11.解:由题意得:∠CDO=90°﹣α,
∴∠BDC=180°﹣∠CDO=90°+α,
∵∠BDC的平分线DF与OE交于点E,
∴∠BDE=∠CDE=∠BDC=45°+0.5α,
∵∠BDE是△DEO的一个外角,
∴∠DEO=∠BDE﹣∠DOE
=45°+0.5α﹣30°
=15°+0.5α,
∵CE⊥DE,
∴∠OEC=90°﹣∠DEO
=75°﹣0.5α,
∴2∠OEC+α
=2×(75°﹣0.5α)+α
=150°﹣α+α
=150°.
故选:C.
12.解:设∠ABC=x,∠E=y,则∠BAC=x+102°,∠D=y+27°.
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ACB=180°﹣(∠ABC+∠BAC)=78°﹣2x°.
∵AE平分∠CAG,
∴∠GAE===39°﹣.
同理可得:∠DBF=90°﹣.
∵∠GAE=∠ABC+∠E,
∴39°﹣=x+y.
∵∠DBF=∠D+∠ACB,
∴90°﹣=y+27°+78°﹣2x.
∴x=18°.
∴∠ACB=78°﹣2x=78°﹣2×18°=42°.
故选:D.
13.解:∵∠B=28°,将△ABC沿直线m翻折,点B落在点D的位置,
∴∠D=∠B=28°,
∵∠1=∠B+∠BEF,∠BEF=∠2+∠D,
∴∠1=∠B+∠2+∠D,
∴∠1﹣∠2=∠B+∠D=28°+28°=56°,
故选:D.
14.解:如图:
∵AE平分∠BAC,BF平分∠ABD,
∴∠CAE=∠BAE,∠1=∠2,
设∠CAE=∠BAE=x,∠C=y,∠ABC=3y,
由外角的性质得:
∠1=∠BAE+∠G=x+20,∠2=∠ABD=(2x+y)=x+y,
∴x+20=x+y,解得y=40°,
∴∠1=∠2=(180°﹣∠ABC)=×(180°﹣120°)=30°,
∴∠DFB=60°.
故选:C.
15.解:连接BC.
∵∠BDC=140°,
∴∠DBC+∠DCB=180°﹣140°=40°,
∵∠BGC=110°,
∴∠GBC+∠GCB=180°﹣110°=70°,
∵BF是∠ABD的平分线,CE是∠ACD的平分线,
∴∠GBD+∠GCD=∠ABD+∠ACD=30°,
∴∠ABC+∠ACB=100°,
∴∠A=180°﹣100°=80°.
故选:D.
二.填空题(共6小题满分30分)
16.解:∵CD平分∠ACB,BE平分∠MBC,
∴∠ACB=2∠DCB,∠MBC=2∠CBE,
∵∠MBC=2∠CBE=∠A+∠ACB,∠CBE=∠D+∠DCB,
∴2∠CBE=∠D+∠DCB,
∴∠MBC=2∠D+∠ACB,
∴2∠D+∠ACB=∠A+∠ACB,
∴∠A=2∠D,
∵∠A=100°,
∴∠D=50°.
故答案为:50°.
17.解:如图,
∵BF,CF分别平分∠EBC,∠ECQ,
∴∠5=∠6,∠2=∠3+∠4,
∵∠3+∠4=∠5+∠F,2∠2=2∠5+∠E,
∴2∠F=∠E=32°,
∵BE,CE分别平分∠MBC,∠BCN,
∴∠5+∠6=,,
∴,
∵∠E=180°﹣(∠5+∠6+∠1)=32°,
∴∠5+∠6+∠1=148°,
∴∠MBC+∠NCB=2(∠5+∠6+∠1)=296°,
∵BD,CD分别平分∠ABC,ACB,
∴∠DBC=,,
∴∠DBC+∠DCB=180°﹣∠MBC+180°﹣∠NCB=360°﹣(∠MBC+∠NCB)=64°,
∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣2(∠DBC+∠DCB)=52°,
故答案为:52°.
18.解:如图,过P作PG⊥BD于点G,过P作PF⊥BE于点F,
∵PH⊥AC,PA、PC分别是∠DAC与∠ACE的平分线,
∴PG=PH,PH=PF,
∴PG=PF,
∴BP是∠ABC的角平分线,
∴∠ABP==30°,
故①正确,
∵∠ABC=∠ACB=60°,
∴∠BAC=60°,
∴∠DAC=∠ACE=120°,
∵PA、PC分别是∠DAC与∠ACE的平分线
∴∠PAC=∠PCA=60°,
∴∠APC=60°,
故②正确,
∵∠APC=∠PCE,
∴PA∥BC,
故③正确,
故答案为:①、②、③.
19.解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
同理可得∠A2=∠A1,∠A3=∠A2,……
则∠A2021=∠A=.
故答案为:.
20.解:连接BG、CG,如图所示:
由折叠的性质得:BD=CD=GD,
∴∠BGC=90°,∠GBC+∠GCB=90°,
又由折叠的性质得:EG=EB,FG=FC,
∴∠EBG=∠EGB,∠FGC=∠FCG,
∵∠AEG=2∠EBG,∠AFG=2∠FCG,∠AEG+∠AFG=54°,
∴2∠EBG+2∠FCG=54°,
∴∠EBG+∠FCG=27°,
∴∠ABC+∠ACB=∠EBG+∠FCG+∠GBC+∠GCB=27°+90°=117°,
∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣117°=63°,
另一种解法:由题意得:∠EGF=∠B+∠C=180°﹣∠A=∠A+∠AEG+∠AFG,
∴∠A=.
故答案为:63.
21.解:∵BD平分∠ABC,CE平分∠ACB,
∴∠MBC=∠ABC,∠MCB=∠ACB,
∴∠BMC=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A=120°,
∴∠1+∠BMN=120°①,
∵MN⊥BC,
∴∠2+∠BMN=90°②,
①﹣②得:∠1﹣∠2=30°.
故答案为:30
三.解答题(共4小题满分45分)
22.解:∵DF平分∠ADE,BF平分∠ABC,
∴∠ADE=2∠ADF,∠ABC=2∠ABF,
∵DE∥BC,
∴∠BCD=∠ADE,
∴∠BCD=∠ADE=2∠ADF,
∵∠ABF+∠A=∠F+∠ADE,
∴∠ABF=∠F+∠ADE﹣n°,
∠BCD=∠A+∠ABC,
∴2∠ADF=n°+2∠ABF,
∴2∠ADF=n°+2(∠F+∠ADE﹣n°)
=n°+2∠F+2∠ADE﹣2n°,
∴∠F=n°.
23.解:(1 )猜想:.
证明∵OB平分∠ABC,OC平分∠ACB,
∴,,
∴∠O=180°﹣(∠OBC+∠OCB)
=
=
=.
(2)如图2所示.∵OB平分∠ABC,OC平分∠ACM
∴,∠ACO=∠ACM.
∴∠O=180°﹣∠OBC﹣∠OCB
=180°﹣∠ABC﹣∠ACB﹣∠ACM.
∵∠ACM=180°﹣∠ACB,
∴∠O=180°﹣∠ABC﹣∠ACB﹣(180°﹣∠ACB)
=180°﹣∠ABC﹣∠ACB﹣90°+∠ACB
=90°﹣∠ABC﹣∠ACB
=90°﹣(∠ABC+∠ACB)
=90°﹣(180°﹣∠A)
=∠A.
当∠A=60°时,
∠O=30°.
故答案为:30°.
如图3所∵OB平分∠EBC,OC平分∠FCB,
∴∠CBO=∠EBC,∠BCO=∠BCF.
∴∠O=180°﹣∠OBC﹣∠OCB
=180°﹣∠EBC﹣∠BCF.
∵∠EBC=180°﹣∠ABC,∠BCF=180°﹣∠ACB,
∴∠O=180°﹣(180°﹣∠ABC)﹣(180°﹣∠ACB)
=180°﹣90°+∠ABC﹣90°+∠ACB
=∠ABC+∠ACB
=(∠ABC+∠ACB)
=(180°﹣∠A)
=90°﹣∠A.
当∠A=60°时,
∠O=60°.
故答案为:60°.
24.解:(1)110°
理由为∵∠A=40°,
∴∠ABC+∠ACB=180°﹣40°=140°,
∵角平分线BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB)=70°,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=110°,
故答案为:110°,
(2)∠BOC=90°+,
理由为∵∠A=α,
∴∠ABC+∠ACB=180°﹣α,
∵角平分线BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=∠ABC++∠ACB=(∠ABC+∠ACB)=(180°﹣α)=90°﹣,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=90+,
故答案为:∠BOC=90°+,
(3)∠BAC=2β,
由(2)结论可知∠BOC=90°+,
∴∠BAC=2∠BOC﹣180°,
∵OB、BF分别平分∠ABC和∠ABE,
∴∠ABO=∠ABC,∠ABF=∠ABE,
∴∠OBF=∠ABO+∠ABF=(∠ABC+∠ABE)=×180°=90°,
∵OD⊥OB,
∴∠BOD=90°,
∴BF∥OD,
∴∠COD=∠F=β,
∴∠BOC=∠BOD+∠COD=90°+β,
∵∠BAC=2∠BOC﹣180°,
∴∠BAC=2∠BOC﹣180°=2β,
故答案为:∠BAC=2β.
25.解:(1)∵MN⊥PQ,
∴∠AOB=90°,
∵∠BAO=40°,
∴∠ABO=90°﹣∠OAB=50°,
∵AI平分∠BAO,BI平分∠ABO,
∴∠IBA=∠ABO=25°,∠IAB=∠OAB=20°,
∴∠AIB=180°﹣(∠IBA+∠IAB)=135°.
(2)①∵∠MBA=∠AOB+∠BAO=90°+40°=130°,
∵AI平分∠BAO,BC平分∠ABM,
∴∠CBA=∠MBA=65°,∠BAI=∠BAO=20°,
∵∠CBA=∠D+∠BAD,
∴∠D=45°,
故答案为:45.
②不变,
理由:∵∠D=∠CBA﹣∠BAD=∠MBA﹣∠BAO=(∠MBA﹣∠BAO)=∠AOB=×90°=45°,
∴点A、B在运动的过程中,∠ADB=45°.
一.选择题(共15小题满分45分)
1.BP是∠ABC的平分线,CP是∠ACB的邻补角的平分线,∠ABP=20°,∠ACP=50°,则∠P=( )
A.30° B.40° C.50° D.60°
2.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=70°,则∠BOC的度数为( )
A.125° B.130° C.135° D.140°
3.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若∠DBC=54°,则∠A的度数为( )
A.36° B.44° C.27° D.54°
4.如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,得∠A1,∠A1BC与∠A1CD的平分线相交于点A2,得∠A2,…,∠A3BC与∠A3CD的平分线相交于点A4,得∠A4,则∠A4的度数为( )
A.5° B.4° C.8° D.16°
5.如图,点A、C在∠FBD的两条边BF、BD上,BE平分∠FBD,CE平分∠ACD,连接AE,若∠BEC=35°,则∠FAE的度数为( )
A.35° B.45° C.55° D.65°
6.如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=120°,则∠1+∠2的度数为( )
A.90° B.100° C.110° D.120°
7.如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠ADE的度数为( )
A.100° B.110° C.120° D.130°
8.已知:如图所示,将△ABC的∠C沿DE折叠,点C落在点C'处,若设∠C=α,∠AEC′=β,∠BDC'=γ,则下列关系成立的是( )
A.2α=β+γ B.α=β+γ C.α+β+γ=180° D.α+β=2γ
9.如图,在△ABC中,∠A=30°,若沿图中虚线截去∠A,则∠1+∠2=( )
A.150° B.200° C.210° D.240°
10.如图,三角形ABC中,角平分线BE、CD分别平分∠ABC和∠ACB相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=∠CGE.其中正确的结论是( )
A.①③④ B.①②③ C.②④ D.①③
11.如图,在竖直墙角AOB中,可伸长的绳子CD的端点C固定在OA上,另一端点D在OB上滑动,在保持绳子拉直的情况下,∠BOE=30°,∠BDC的平分线DF与OE交于点E,∠DCO=α,当CE⊥DE时,则2∠OEC+α=( )
A.120° B.135° C.150° D.152°
12.如图,射线BD,AE分别是△ABC的外角∠ABF,∠CAG的角平分线,射线BD与直线AC交于点D,射线AE与直线BC交于点E,若∠BAC=∠ABC+102°,∠D=∠E+27°,则∠ACB的度数为( )
A.39° B.40° C.41° D.42°
13.如图,在△ABC中,∠B=28°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.42° B.46° C.52° D.56°
14.如图,在△ABC中,AE平分∠BAC,AD⊥BC于点D.∠ABD的角平分线BF所在直线与射线AE相交于点G,若∠ABC=3∠C,且∠G=20°,则∠DFB的度数为( )
A.50° B.55° C.60° D.65°
15.如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
A.50° B.55° C.70° D.80°
二.填空题(共6小题满分30分)
16.如图,∠MAN=100°,点B,C是射线AM.AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小为 .
17.如图,在△ABC中,∠F=16°,BD、CD分别平分∠ABC,∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC,∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠A= .
18.如图,△ABC的两条外角平分线AP,CP相交于点P,PH⊥AC于点H.若∠ABC=∠ACB=60°,则下列结论:①∠ABP=30°;②∠APC=60°;③PA∥BC,其中正确的结论有 .(填序号)
19.如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,…,若∠A=α,则∠A2021为 .
20.如图,将△ABC沿DE、DF翻折,使顶点B、C都落于点G处,且线段BD、CD翻折后重合于DG,若∠AEG+∠AFG=54°,则∠A= 度.
21.如图,在△ABC中,BD平分∠ABC,CE平分∠ACB,BD与CE交于点M.若MN⊥BC于N,∠A=60°,则∠1﹣∠2= 度.
三.解答题(共4小题满分45分)
22.如图,在△ABC中,点D是AC延长线上的一点,过点D作DE∥BC,DF平分∠ADE,BF平分∠ABC.设∠A=n°,求∠F的度数(用含n的式子表示).
23.已知在△ABC中,图1,图2,图3中的△ABC的内角平分线或外角平分线交于点O.
(1)如图1,点O是△ABC的两个内角平分线的交点,猜想∠O与∠A之间的数量关系,并加以证明.
(2)请直接写出结果.如图2,若∠A=60°,△ABC的内角平分线与外角平分线交于点O,则∠O= ;如图3,若∠A=60°,△ABC的两个外角平分线交于点O,则∠O= .
24.嘉琪在学习过程中,对教材的一个有趣的问题做如下探究:
【习题回顾】
已知:如图1,在△ABC中,∠A=40°,角平分线BO、CO交于点O.求∠BOC的度数.
(1)请直接写出∠BOC= .
【变式思考】
(2)若∠A=α,请猜想∠BOC与α的关系,并说明理由;
【拓展延伸】
(3)已知:如图2,在△ABC中,角平分线BO、CO交于点O,OD⊥OB,交边BC于点D,作∠ABE的平分线交CO的延长线于点F.若∠F=β,猜想∠BAC与β的关系,并说明理由.
25.∠MOQ=90°,点A,B分别在射线OM、OQ上运动(不与点O重合).
(1)如图1,AI平分∠BAO,BI平分∠ABO,若∠BAO=40°,求∠AIB的度数.
(2)如图2,AI平分∠BAO,BC平分∠ABM,BC的反向延长线交AI于点D.
①若∠BAO=40°,则∠ADB= °;
②点A、B在运动的过程中,∠ADB是否发生变化,若不变,试求∠ADB的度数;若变化,请说明变化规律.
参考答案
一.选择题(共15小题,满分45分)
1.解:∵CP是∠ACM的角平分线,∠ACP=90°,
∴∠ACM=2∠ACP=100°,
∴∠ACB=80°,
∵BP是∠ABC的角平分线,∠ABP=20°,
∴∠CBP=∠ABP=20°,
∴∠P=180°﹣∠CBP﹣∠ACB﹣∠ACP
=180°﹣20°﹣80°﹣50°
=30°,
故选:A.
2.解:∵∠A=70°,
∴∠ABC+∠ACB=180°﹣∠A=110°,
∵BO、CO分别是∠ABC、∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°.
故选:A.
3.解:∵BD⊥CD,
∴∠D=90°.
∵∠DBC=54°,
∴∠DCB=90°﹣54°=36°.
∵CD平分∠ACB,
∴∠ACB=72°.
∵∠A=∠ABD,∠A+∠ABC+∠ACB=180°,
∴∠A+∠A+54°+72°=180°.
∴∠A=27°.
故选:C.
4.解:∵∠ABC与∠ACD的平分线交于点A1,
∴∠A1BC=,,
由三角形的外角性质得,
∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∴,
=,
∴∠A1==32°,
同理∠A4==4°,
故选:B.
5.解:∵BE平分∠FBD,CE平分∠ACD,
∴∠ABC=2∠EBD,∠ACD=2∠ECD,AE平分∠FAC,
∵∠ACD=∠ABC+∠BAC,∠ECD=∠EBC+∠BEC,
∴2∠ECD=2∠EBD+∠BAC,2∠ECD=2∠EBD+2∠BEC,
∴∠BAC=2∠BEC,
∵∠BEC=35°,
∴∠BAC=2×35°=70°,
∵∠BAC+∠FAC=180°,
∴∠FAC=180°﹣70°=110°,
∵AE平分∠FAC,
∴∠FAE=∠FAC=55°.
故选:C.
6.解:如图,连接AA',
∵A'B平分∠ABC,A'C平分∠ACB,
∴∠A'BC=∠ABC,∠A'CB=∠ACB,
∵∠BA'C=120°,
∴∠A'BC+∠A'CB=180°﹣120°=60°,
∴∠ABC+∠ACB=120°,
∴∠BAC=180°﹣120°=60°,
∵沿DE折叠,
∴∠DAA'=∠DA'A,∠EAA'=∠EA'A,
∵∠1=∠DAA'+∠DA'A=2∠DAA',∠2=∠EAA'+∠EA'A=2∠EAA',
∴∠1+∠2=2∠DAA'+2∠EAA'=2∠BAC=2×60°=120°,
故选:D.
7.解:∵∠B=40°,∠C=30°,
∴∠BAC=110°,
由折叠的性质得,∠E=∠C=30°,∠EAD=∠CAD,∠ADE=∠ADC,
∵DE∥AB,
∴∠BAE=∠E=30°,
∴∠CAD=40°,
∴∠ADE=∠ADC=180°﹣∠CAD﹣∠C=110°,
故选:B.
8.解:由折叠的性质知:∠C=∠C′=α.
∵∠AEC′+∠CEC′=180°,∠BDC′+∠CDC′=180°,
∴β=180°﹣∠CEC′,γ=180°﹣∠CDC′.
∴β+γ=360°﹣∠CEC′﹣∠CDC′.
∵∠C+∠CEC′+CDC′+∠C′=360°,
∴2α=360°﹣∠CEC′﹣CDC′.
∴β+γ=2α.
故选:A.
9.解:如图:∠1+∠3=180°,∠2+∠4=180°,
∴∠1+∠2+∠3+∠4=360°,
∵∠A+∠3+∠4=180°,∠A=30°,
∴∠3+∠4=150°,
∴∠1+∠2=210°.
故选:C.
10.解:①∵EG∥BC,
∴∠CEG=∠ACB,
又∵CD是△ABC的角平分线,
∴∠CEG=∠ACB=2∠DCB,故①正确;
②∵∠CEG=∠ACB,而∠GEC与∠GCE不一定相等,
∴CA不一定平分∠BCG,故②错误;
③∵∠A=90°,
∴∠ADC+∠ACD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC+∠BCD=90°.
∵EG∥BC,且CG⊥EG,
∴∠GCB=90°,即∠GCD+∠BCD=90°,
∴∠ADC=∠GCD,故③正确;
④∵∠ABC+∠ACB=90°,
∵CD平分∠ACB,BE平分∠ABC,
∴∠EBC=∠ABC,∠DCB=∠ACB,
∴∠DFB=∠EBC+∠DCB=(∠ABC+∠ACB)=45°,
∵∠CGE=90°,
∴∠DFB=∠CGE,故④正确.
综上所述,正确的有:①③④.
故选:A.
11.解:由题意得:∠CDO=90°﹣α,
∴∠BDC=180°﹣∠CDO=90°+α,
∵∠BDC的平分线DF与OE交于点E,
∴∠BDE=∠CDE=∠BDC=45°+0.5α,
∵∠BDE是△DEO的一个外角,
∴∠DEO=∠BDE﹣∠DOE
=45°+0.5α﹣30°
=15°+0.5α,
∵CE⊥DE,
∴∠OEC=90°﹣∠DEO
=75°﹣0.5α,
∴2∠OEC+α
=2×(75°﹣0.5α)+α
=150°﹣α+α
=150°.
故选:C.
12.解:设∠ABC=x,∠E=y,则∠BAC=x+102°,∠D=y+27°.
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ACB=180°﹣(∠ABC+∠BAC)=78°﹣2x°.
∵AE平分∠CAG,
∴∠GAE===39°﹣.
同理可得:∠DBF=90°﹣.
∵∠GAE=∠ABC+∠E,
∴39°﹣=x+y.
∵∠DBF=∠D+∠ACB,
∴90°﹣=y+27°+78°﹣2x.
∴x=18°.
∴∠ACB=78°﹣2x=78°﹣2×18°=42°.
故选:D.
13.解:∵∠B=28°,将△ABC沿直线m翻折,点B落在点D的位置,
∴∠D=∠B=28°,
∵∠1=∠B+∠BEF,∠BEF=∠2+∠D,
∴∠1=∠B+∠2+∠D,
∴∠1﹣∠2=∠B+∠D=28°+28°=56°,
故选:D.
14.解:如图:
∵AE平分∠BAC,BF平分∠ABD,
∴∠CAE=∠BAE,∠1=∠2,
设∠CAE=∠BAE=x,∠C=y,∠ABC=3y,
由外角的性质得:
∠1=∠BAE+∠G=x+20,∠2=∠ABD=(2x+y)=x+y,
∴x+20=x+y,解得y=40°,
∴∠1=∠2=(180°﹣∠ABC)=×(180°﹣120°)=30°,
∴∠DFB=60°.
故选:C.
15.解:连接BC.
∵∠BDC=140°,
∴∠DBC+∠DCB=180°﹣140°=40°,
∵∠BGC=110°,
∴∠GBC+∠GCB=180°﹣110°=70°,
∵BF是∠ABD的平分线,CE是∠ACD的平分线,
∴∠GBD+∠GCD=∠ABD+∠ACD=30°,
∴∠ABC+∠ACB=100°,
∴∠A=180°﹣100°=80°.
故选:D.
二.填空题(共6小题满分30分)
16.解:∵CD平分∠ACB,BE平分∠MBC,
∴∠ACB=2∠DCB,∠MBC=2∠CBE,
∵∠MBC=2∠CBE=∠A+∠ACB,∠CBE=∠D+∠DCB,
∴2∠CBE=∠D+∠DCB,
∴∠MBC=2∠D+∠ACB,
∴2∠D+∠ACB=∠A+∠ACB,
∴∠A=2∠D,
∵∠A=100°,
∴∠D=50°.
故答案为:50°.
17.解:如图,
∵BF,CF分别平分∠EBC,∠ECQ,
∴∠5=∠6,∠2=∠3+∠4,
∵∠3+∠4=∠5+∠F,2∠2=2∠5+∠E,
∴2∠F=∠E=32°,
∵BE,CE分别平分∠MBC,∠BCN,
∴∠5+∠6=,,
∴,
∵∠E=180°﹣(∠5+∠6+∠1)=32°,
∴∠5+∠6+∠1=148°,
∴∠MBC+∠NCB=2(∠5+∠6+∠1)=296°,
∵BD,CD分别平分∠ABC,ACB,
∴∠DBC=,,
∴∠DBC+∠DCB=180°﹣∠MBC+180°﹣∠NCB=360°﹣(∠MBC+∠NCB)=64°,
∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣2(∠DBC+∠DCB)=52°,
故答案为:52°.
18.解:如图,过P作PG⊥BD于点G,过P作PF⊥BE于点F,
∵PH⊥AC,PA、PC分别是∠DAC与∠ACE的平分线,
∴PG=PH,PH=PF,
∴PG=PF,
∴BP是∠ABC的角平分线,
∴∠ABP==30°,
故①正确,
∵∠ABC=∠ACB=60°,
∴∠BAC=60°,
∴∠DAC=∠ACE=120°,
∵PA、PC分别是∠DAC与∠ACE的平分线
∴∠PAC=∠PCA=60°,
∴∠APC=60°,
故②正确,
∵∠APC=∠PCE,
∴PA∥BC,
故③正确,
故答案为:①、②、③.
19.解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
同理可得∠A2=∠A1,∠A3=∠A2,……
则∠A2021=∠A=.
故答案为:.
20.解:连接BG、CG,如图所示:
由折叠的性质得:BD=CD=GD,
∴∠BGC=90°,∠GBC+∠GCB=90°,
又由折叠的性质得:EG=EB,FG=FC,
∴∠EBG=∠EGB,∠FGC=∠FCG,
∵∠AEG=2∠EBG,∠AFG=2∠FCG,∠AEG+∠AFG=54°,
∴2∠EBG+2∠FCG=54°,
∴∠EBG+∠FCG=27°,
∴∠ABC+∠ACB=∠EBG+∠FCG+∠GBC+∠GCB=27°+90°=117°,
∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣117°=63°,
另一种解法:由题意得:∠EGF=∠B+∠C=180°﹣∠A=∠A+∠AEG+∠AFG,
∴∠A=.
故答案为:63.
21.解:∵BD平分∠ABC,CE平分∠ACB,
∴∠MBC=∠ABC,∠MCB=∠ACB,
∴∠BMC=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A=120°,
∴∠1+∠BMN=120°①,
∵MN⊥BC,
∴∠2+∠BMN=90°②,
①﹣②得:∠1﹣∠2=30°.
故答案为:30
三.解答题(共4小题满分45分)
22.解:∵DF平分∠ADE,BF平分∠ABC,
∴∠ADE=2∠ADF,∠ABC=2∠ABF,
∵DE∥BC,
∴∠BCD=∠ADE,
∴∠BCD=∠ADE=2∠ADF,
∵∠ABF+∠A=∠F+∠ADE,
∴∠ABF=∠F+∠ADE﹣n°,
∠BCD=∠A+∠ABC,
∴2∠ADF=n°+2∠ABF,
∴2∠ADF=n°+2(∠F+∠ADE﹣n°)
=n°+2∠F+2∠ADE﹣2n°,
∴∠F=n°.
23.解:(1 )猜想:.
证明∵OB平分∠ABC,OC平分∠ACB,
∴,,
∴∠O=180°﹣(∠OBC+∠OCB)
=
=
=.
(2)如图2所示.∵OB平分∠ABC,OC平分∠ACM
∴,∠ACO=∠ACM.
∴∠O=180°﹣∠OBC﹣∠OCB
=180°﹣∠ABC﹣∠ACB﹣∠ACM.
∵∠ACM=180°﹣∠ACB,
∴∠O=180°﹣∠ABC﹣∠ACB﹣(180°﹣∠ACB)
=180°﹣∠ABC﹣∠ACB﹣90°+∠ACB
=90°﹣∠ABC﹣∠ACB
=90°﹣(∠ABC+∠ACB)
=90°﹣(180°﹣∠A)
=∠A.
当∠A=60°时,
∠O=30°.
故答案为:30°.
如图3所∵OB平分∠EBC,OC平分∠FCB,
∴∠CBO=∠EBC,∠BCO=∠BCF.
∴∠O=180°﹣∠OBC﹣∠OCB
=180°﹣∠EBC﹣∠BCF.
∵∠EBC=180°﹣∠ABC,∠BCF=180°﹣∠ACB,
∴∠O=180°﹣(180°﹣∠ABC)﹣(180°﹣∠ACB)
=180°﹣90°+∠ABC﹣90°+∠ACB
=∠ABC+∠ACB
=(∠ABC+∠ACB)
=(180°﹣∠A)
=90°﹣∠A.
当∠A=60°时,
∠O=60°.
故答案为:60°.
24.解:(1)110°
理由为∵∠A=40°,
∴∠ABC+∠ACB=180°﹣40°=140°,
∵角平分线BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB)=70°,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=110°,
故答案为:110°,
(2)∠BOC=90°+,
理由为∵∠A=α,
∴∠ABC+∠ACB=180°﹣α,
∵角平分线BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=∠ABC++∠ACB=(∠ABC+∠ACB)=(180°﹣α)=90°﹣,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=90+,
故答案为:∠BOC=90°+,
(3)∠BAC=2β,
由(2)结论可知∠BOC=90°+,
∴∠BAC=2∠BOC﹣180°,
∵OB、BF分别平分∠ABC和∠ABE,
∴∠ABO=∠ABC,∠ABF=∠ABE,
∴∠OBF=∠ABO+∠ABF=(∠ABC+∠ABE)=×180°=90°,
∵OD⊥OB,
∴∠BOD=90°,
∴BF∥OD,
∴∠COD=∠F=β,
∴∠BOC=∠BOD+∠COD=90°+β,
∵∠BAC=2∠BOC﹣180°,
∴∠BAC=2∠BOC﹣180°=2β,
故答案为:∠BAC=2β.
25.解:(1)∵MN⊥PQ,
∴∠AOB=90°,
∵∠BAO=40°,
∴∠ABO=90°﹣∠OAB=50°,
∵AI平分∠BAO,BI平分∠ABO,
∴∠IBA=∠ABO=25°,∠IAB=∠OAB=20°,
∴∠AIB=180°﹣(∠IBA+∠IAB)=135°.
(2)①∵∠MBA=∠AOB+∠BAO=90°+40°=130°,
∵AI平分∠BAO,BC平分∠ABM,
∴∠CBA=∠MBA=65°,∠BAI=∠BAO=20°,
∵∠CBA=∠D+∠BAD,
∴∠D=45°,
故答案为:45.
②不变,
理由:∵∠D=∠CBA﹣∠BAD=∠MBA﹣∠BAO=(∠MBA﹣∠BAO)=∠AOB=×90°=45°,
∴点A、B在运动的过程中,∠ADB=45°.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
