24.1.3 弧、弦、圆心角 同步练习 2021—2022学年人教版九年级数学上册(word版含答案)
文档属性
| 名称 | 24.1.3 弧、弦、圆心角 同步练习 2021—2022学年人教版九年级数学上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 294.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 07:41:10 | ||
图片预览



文档简介
2021——2022学年度人教版九年级数学上册 第二十四章 圆 24.1.3 弧、弦、圆心角 同步练习
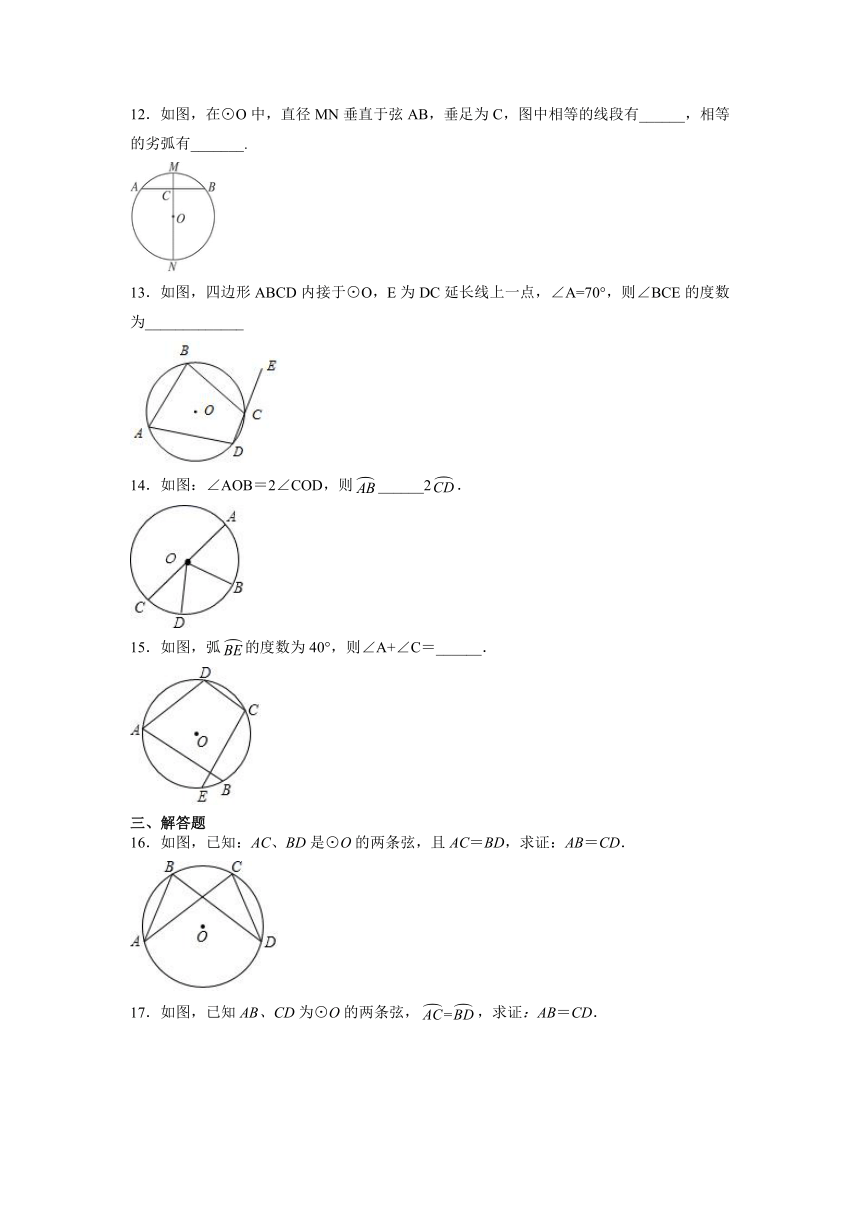
一、选择题
1.下列语句中不正确的有( )
①相等的圆心角所对的弧相等; ②平分弦的直径垂直于弦;③弧长相等的弧是等弧; ④半圆是弧
A.1个 B.2个 C.3个 D.4个
2.下列五个命题:①直径是弦,②优弧大于劣弧,③等弧的弧长相等,④平分弦的直径垂直于弦,⑤等弧所对的弦相等.其中正确的有( )个.
A.2 B.3 C.4 D.5
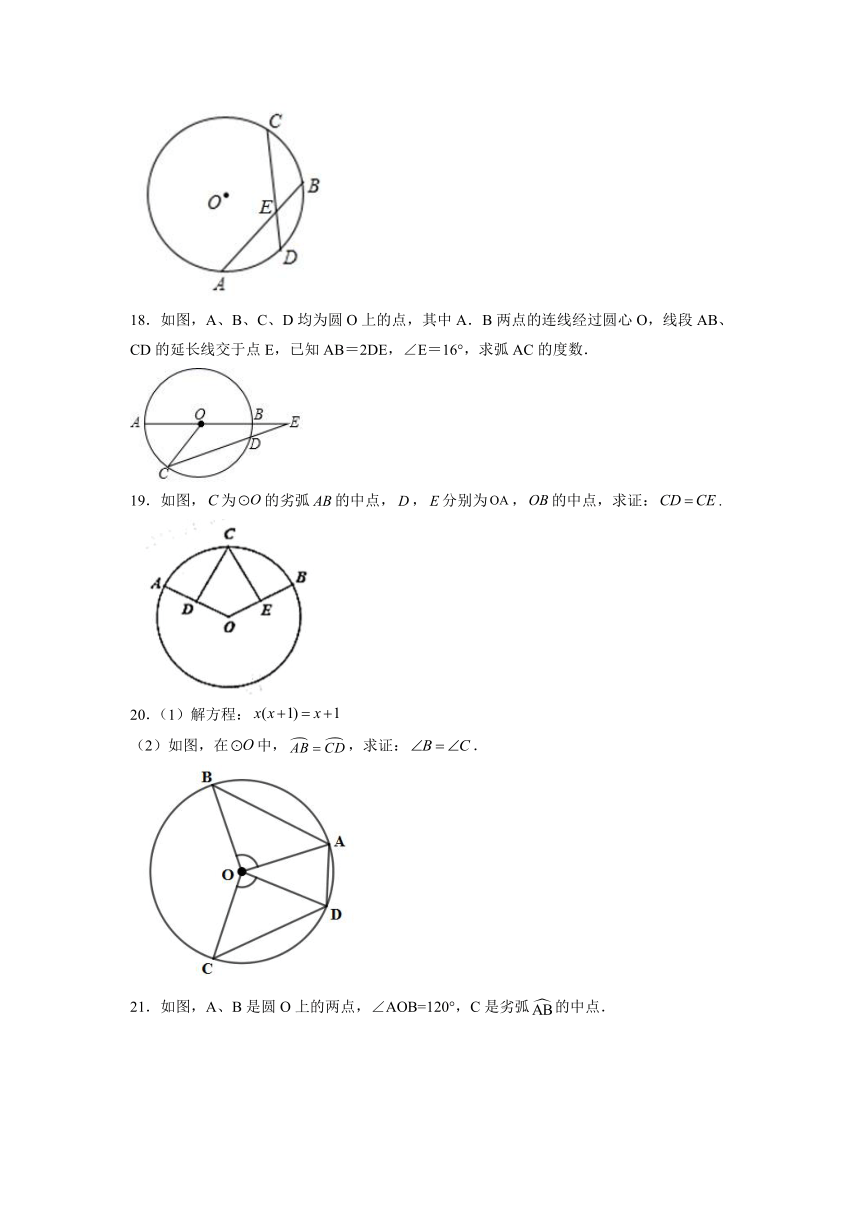
3.在⊙O中,M为的中点,则下列结论正确的是( )
A.AB>2AM B.AB=2AM
C.AB<2AM D.AB与2AM的大小不能确定
4.下列说法正确的是( )
A.相等的圆周角所对的弧相等
B.相等的弦所对的弧相等
C.平分弦的直径一定垂直于弦
D.任意三角形一定有一个外接圆
5.如图,在△ABC中,∠C=90°,的度数为α,以点C为圆心,BC长为半径的圆交AB于点D,交AC于点E,则∠A的度数为( )
A.45 -α B.α C.45 +α D.25 +α
6.如图,中,如果,那么( )
A. B. C. D.
7.如图,OA、OB、OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC,则下列结论正确的是( )个.
①AB=2BC;②=2;③∠ACB=2∠CAB;④∠ACB=∠BOC.
A.1 B.2 C.3 D.4
8.如图,在⊙O中,AB是直径,OD⊥AC于点E,交⊙O于点D,则下列结论错误的是( )
A.AD=CD B. C.BC=2EO D.EO=DE
9.如图,半径为5的中,弦所对的圆心角分别是.已知,,则弦的弦心距等于( )
A. B. C.4 D.3
10.如图,是的直径,点,在上,, ,,则的半径为( )
A. B. C. D.
二、填空题
11.把一个圆分成4个扇形,它们分别占整个圆的10%,20%,30%,40%,那么这四个扇形的圆心角分别是_______.
12.如图,在⊙O中,直径MN垂直于弦AB,垂足为C,图中相等的线段有______,相等的劣弧有_______.
13.如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=70°,则∠BCE的度数为_____________
14.如图:∠AOB=2∠COD,则______2.
15.如图,弧的度数为40°,则∠A+∠C=______.
三、解答题
16.如图,已知:AC、BD是⊙O的两条弦,且AC=BD,求证:AB=CD.
17.如图,已知AB、CD为⊙O的两条弦,,求证:AB=CD.
18.如图,A、B、C、D均为圆O上的点,其中A.B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=16°,求弧AC的度数.
19.如图,为的劣弧的中点,,分别为,的中点,求证:.
20.(1)解方程:
(2)如图,在中,,求证:.
21.如图,A、B是圆O上的两点,∠AOB=120°,C是劣弧的中点.
(1)试判断四边形OACB的形状,并说明理由;
(2)延长OA至P,使得AP=OA,连接PC,若PC为,求BC长.
22.阅读以下内容,并回答问题:若一个三角形的两边的平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形.
(1)命题“等边三角形一定是奇异三角形”是__________命题(填“真”或“假”);
(2)在中,已知的内角,所对边的长分别为,且,若是奇异三角形,求;
(3)如图,已知是上一点(点不与点重合),是半圆的中点,在直径的两侧,若存在点,使.求证:是奇异三角形.
23.如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=,将△ABC绕点P旋转180°,得到△MCB.
(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,判断四边形ACMB的形状,并说明理由.
(3)求出点M的坐标.
【参考答案】
1.C 2.B 3.C 4.D 5.A 6.C 7.C 8.D 9.C 10.D
11.36°,72°,108°,144°
12.AC=BC 弧AM=弧BM,弧AN=弧BN.
13.70°
14.=
15.160°
16.证明:∵AC=BD
∴
∴
∴
∴AB=CD
17.解:∵,
∴,即,
∴AB=CD.
18.解:连接OD,
∵AB=2DE=2OD,
∴OD=DE,
又∵∠E=16°,
∴∠DOE=∠E=16°,
∴∠ODC=32°,
同理∠C=∠ODC=32°
∴∠AOC=∠E+∠OCE=48°,
∴的度数=48°.
19.证明:为的劣弧的中点,,
连接,
分别为的中点,
,.
在和中,
20.(1)解:,
,
=-1,=1;
(2)证明:∵在⊙O中,,
∴AB=CD,
∴∠AOB=∠COD,
∵OA=OB,OC=OD,
∴在△AOB中,∠B=90° ∠AOB,
在△COD中,∠C=90° ∠COD,
∴∠B=∠C.
21.解:(1)四边形OACB是菱形.
理由:连接OC,
∵∠AOB=120°,C是劣弧的中点,
∴∠AOC=∠BOC=∠AOB=60°,
∵OA=OC=OB,
∴△AOC与△BOC都是等边三角形,
∴AC=OA=OC=OB=BC,
∴四边形OACB是菱形.
(2)∵AP=OA,AC=OA,
∴AP=AC,
∴∠P=∠ACP=∠OAC=30°,
∴∠OCP=90°,
设圆O的半径为x,则OC=x,OP=2x
∴,
∴x=3
∵四边形OACB是菱形.
∴BC=3
22.解:(1)∵若一个三角形的两边的平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形,
∴“等边三角形一定是奇异三角形”是真命题.
故答案为:真.
(2)
①.
是奇异三角形,且
②.
由①②得,
.
(3)证明:由题意知,
∴在中,,在中,.
∵点是半圆的中点,
,
又
是奇异三角形.
23.解:(1)连接PA,如图1所示.
,
.
,
.
,
.
.
.
;
(2)连接AP,延长AP交于点M,连接MB、MC.
如图2所示,线段MB、MC即为所求作.
四边形ACMB是矩形.
理由如下:
由绕点P旋转所得,
四边形ACMB是平行四边形.
是的直径,
.
平行四边形ACMB是矩形;
(3)过点M作,垂足为H,如图2所示.
,
.
.
点M的坐标为
一、选择题
1.下列语句中不正确的有( )
①相等的圆心角所对的弧相等; ②平分弦的直径垂直于弦;③弧长相等的弧是等弧; ④半圆是弧
A.1个 B.2个 C.3个 D.4个
2.下列五个命题:①直径是弦,②优弧大于劣弧,③等弧的弧长相等,④平分弦的直径垂直于弦,⑤等弧所对的弦相等.其中正确的有( )个.
A.2 B.3 C.4 D.5
3.在⊙O中,M为的中点,则下列结论正确的是( )
A.AB>2AM B.AB=2AM
C.AB<2AM D.AB与2AM的大小不能确定
4.下列说法正确的是( )
A.相等的圆周角所对的弧相等
B.相等的弦所对的弧相等
C.平分弦的直径一定垂直于弦
D.任意三角形一定有一个外接圆
5.如图,在△ABC中,∠C=90°,的度数为α,以点C为圆心,BC长为半径的圆交AB于点D,交AC于点E,则∠A的度数为( )
A.45 -α B.α C.45 +α D.25 +α
6.如图,中,如果,那么( )
A. B. C. D.
7.如图,OA、OB、OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC,则下列结论正确的是( )个.
①AB=2BC;②=2;③∠ACB=2∠CAB;④∠ACB=∠BOC.
A.1 B.2 C.3 D.4
8.如图,在⊙O中,AB是直径,OD⊥AC于点E,交⊙O于点D,则下列结论错误的是( )
A.AD=CD B. C.BC=2EO D.EO=DE
9.如图,半径为5的中,弦所对的圆心角分别是.已知,,则弦的弦心距等于( )
A. B. C.4 D.3
10.如图,是的直径,点,在上,, ,,则的半径为( )
A. B. C. D.
二、填空题
11.把一个圆分成4个扇形,它们分别占整个圆的10%,20%,30%,40%,那么这四个扇形的圆心角分别是_______.
12.如图,在⊙O中,直径MN垂直于弦AB,垂足为C,图中相等的线段有______,相等的劣弧有_______.
13.如图,四边形ABCD内接于⊙O,E为DC延长线上一点,∠A=70°,则∠BCE的度数为_____________
14.如图:∠AOB=2∠COD,则______2.
15.如图,弧的度数为40°,则∠A+∠C=______.
三、解答题
16.如图,已知:AC、BD是⊙O的两条弦,且AC=BD,求证:AB=CD.
17.如图,已知AB、CD为⊙O的两条弦,,求证:AB=CD.
18.如图,A、B、C、D均为圆O上的点,其中A.B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=16°,求弧AC的度数.
19.如图,为的劣弧的中点,,分别为,的中点,求证:.
20.(1)解方程:
(2)如图,在中,,求证:.
21.如图,A、B是圆O上的两点,∠AOB=120°,C是劣弧的中点.
(1)试判断四边形OACB的形状,并说明理由;
(2)延长OA至P,使得AP=OA,连接PC,若PC为,求BC长.
22.阅读以下内容,并回答问题:若一个三角形的两边的平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形.
(1)命题“等边三角形一定是奇异三角形”是__________命题(填“真”或“假”);
(2)在中,已知的内角,所对边的长分别为,且,若是奇异三角形,求;
(3)如图,已知是上一点(点不与点重合),是半圆的中点,在直径的两侧,若存在点,使.求证:是奇异三角形.
23.如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=,将△ABC绕点P旋转180°,得到△MCB.
(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,判断四边形ACMB的形状,并说明理由.
(3)求出点M的坐标.
【参考答案】
1.C 2.B 3.C 4.D 5.A 6.C 7.C 8.D 9.C 10.D
11.36°,72°,108°,144°
12.AC=BC 弧AM=弧BM,弧AN=弧BN.
13.70°
14.=
15.160°
16.证明:∵AC=BD
∴
∴
∴
∴AB=CD
17.解:∵,
∴,即,
∴AB=CD.
18.解:连接OD,
∵AB=2DE=2OD,
∴OD=DE,
又∵∠E=16°,
∴∠DOE=∠E=16°,
∴∠ODC=32°,
同理∠C=∠ODC=32°
∴∠AOC=∠E+∠OCE=48°,
∴的度数=48°.
19.证明:为的劣弧的中点,,
连接,
分别为的中点,
,.
在和中,
20.(1)解:,
,
=-1,=1;
(2)证明:∵在⊙O中,,
∴AB=CD,
∴∠AOB=∠COD,
∵OA=OB,OC=OD,
∴在△AOB中,∠B=90° ∠AOB,
在△COD中,∠C=90° ∠COD,
∴∠B=∠C.
21.解:(1)四边形OACB是菱形.
理由:连接OC,
∵∠AOB=120°,C是劣弧的中点,
∴∠AOC=∠BOC=∠AOB=60°,
∵OA=OC=OB,
∴△AOC与△BOC都是等边三角形,
∴AC=OA=OC=OB=BC,
∴四边形OACB是菱形.
(2)∵AP=OA,AC=OA,
∴AP=AC,
∴∠P=∠ACP=∠OAC=30°,
∴∠OCP=90°,
设圆O的半径为x,则OC=x,OP=2x
∴,
∴x=3
∵四边形OACB是菱形.
∴BC=3
22.解:(1)∵若一个三角形的两边的平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形,
∴“等边三角形一定是奇异三角形”是真命题.
故答案为:真.
(2)
①.
是奇异三角形,且
②.
由①②得,
.
(3)证明:由题意知,
∴在中,,在中,.
∵点是半圆的中点,
,
又
是奇异三角形.
23.解:(1)连接PA,如图1所示.
,
.
,
.
,
.
.
.
;
(2)连接AP,延长AP交于点M,连接MB、MC.
如图2所示,线段MB、MC即为所求作.
四边形ACMB是矩形.
理由如下:
由绕点P旋转所得,
四边形ACMB是平行四边形.
是的直径,
.
平行四边形ACMB是矩形;
(3)过点M作,垂足为H,如图2所示.
,
.
.
点M的坐标为
同课章节目录
