28.2解直角三角形及其应用 题型分类训练 2021-2022学年人教版九年级数学下册(word版含解析)
文档属性
| 名称 | 28.2解直角三角形及其应用 题型分类训练 2021-2022学年人教版九年级数学下册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 536.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 07:45:19 | ||
图片预览

文档简介
2021-2022学年人教版九年级数学下册《28.2解直角三角形及其应用》
题型分类训练(附答案)
一.解直角三角形
1.如图,∠ABC=∠BDA=90°,下列线段比值等于sinA的是( )
A. B. C. D.
2.如图,在平面直角坐标系xOy中,直线OA过点(2,1),直线OA与x轴的夹角为α,则tanα的值为( )
A. B. C.2 D.
3.如图,A,B,C是3×1的正方形网格中的三个格点,则tanB的值为( )
A. B. C. D.
4.等腰三角形底边长为10cm,周长为36cm,那么底角的余弦等于( )
A. B. C. D.
5.如图,A、B、D三点在同一水平线上,CD⊥AD,∠A=45°,∠CBD=75°,AB=60m.
(1)求∠ACB的度数;
(2)求线段CB的长度.
6.如图,在△ABC中,AB=AC=10,.求sinA的值.
7.如图,在△ABC中,AD⊥BC于点D,若AD=6.tanC=,BC=12,求cosB的值.
8.根据下列条件,解直角三角形:在Rt△ABC中,∠C=90°,a=8,∠B=60°.
9.如图,在△ABC中,∠ACB=90°,BC=3,AC=4,CD⊥AB,垂足为D,求sin∠ACD和tan∠BCD.
二.解直角三角形的应用
10.某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
A.3.5sin29° B.3.5cos29° C.3.5tan29° D.
11.如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
A. B. C.6cos50° D.
12.学校进行实践活动,喜欢数学的小伟沿笔直的河岸BC进行数学实践活动,如图,河对岸有一码头A,小伟在河岸B处测得∠ABC=45°,沿河岸到达C处,在C处测得∠ACB=30,已知河宽为20米,求B、C之间的距离.
13.如图,某景区门口的柱子上方挂着一块景点宣传牌CD,宣传牌的一侧用绳子AD和BC牵引着两排小风车,经过测量得到如下数据:AM=2米,AB=4米,∠MAD=45°,∠MBC=30°,则CD的长度约为 米.(≈1.73,结果精确到0.1米)
14.如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.(参考数据:tan31°≈0.6,tan50°≈1.2)
(1)求B,C两点间的距离(结果精确到1m);
(2)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
三.解直角三角形的应用-坡度坡角问题
15.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,则AB的长度为( )
A.2m B.4m C.4m D.6m
16.如图,河堤横断面迎水坡AB的坡比是1:,堤高BC=2米,则迎水坡宽度AC的长为( )
A.4米 B.2米 C.米 D.2米
17.如图,在离地面高度5m处引拉线固定电线杆,拉线和地面成60°角,则拉线AC的长是( )
A.10m B.m C.m D.5m
18.有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若坡比为2:5,则此斜坡的水平距离AC为 .
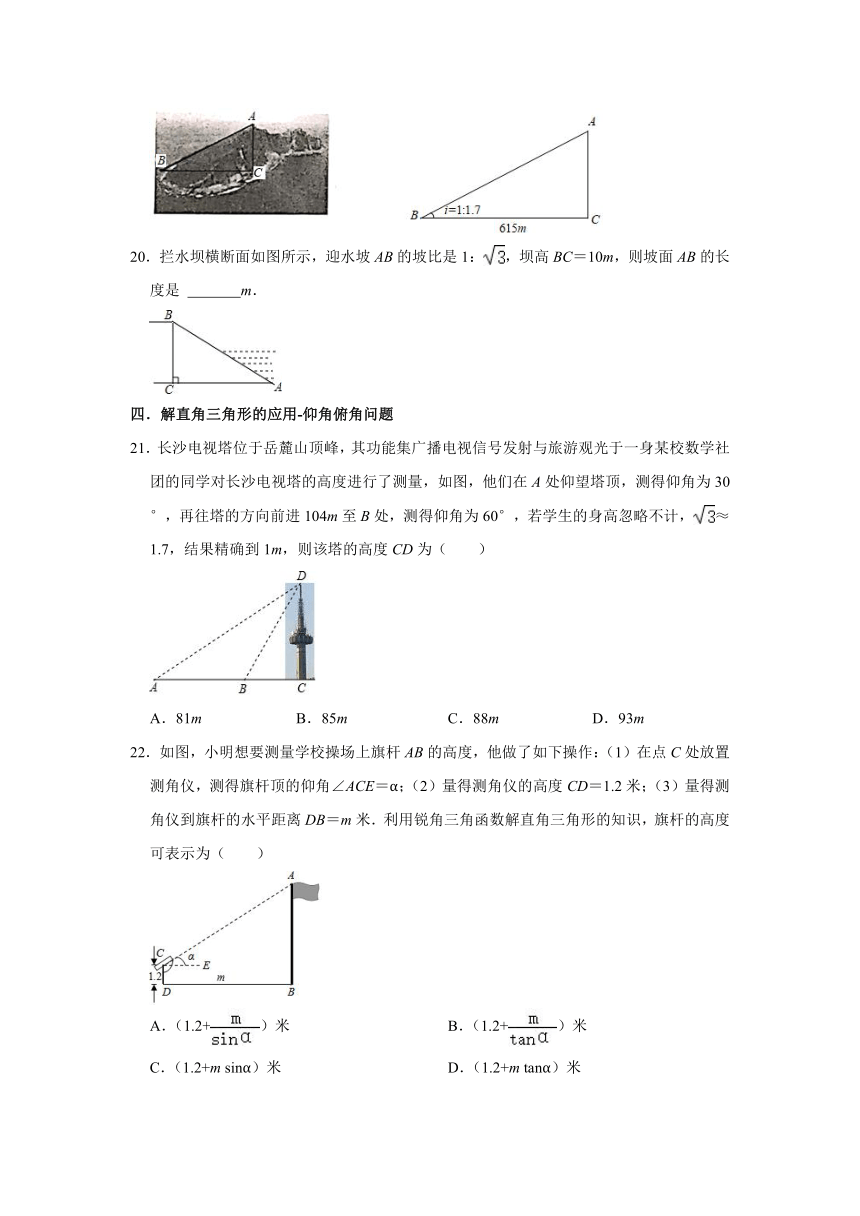
19.钓鱼岛是中国固有领土,2021年4月26日,国家自然资源部发布了钓鱼岛地形地貌调查报告,钓鱼岛中央山脊呈东西走向,北坡稍缓,南坡陡峭,已知主峰高华峰北坡AB坡度i=1:1.7,海平面上BC的水平距离约为615米,则主峰高华峰的高度AC约为 米.(精确到1米)
20.拦水坝横断面如图所示,迎水坡AB的坡比是1:,坝高BC=10m,则坡面AB的长度是 m.
四.解直角三角形的应用-仰角俯角问题
21.长沙电视塔位于岳麓山顶峰,其功能集广播电视信号发射与旅游观光于一身某校数学社团的同学对长沙电视塔的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往塔的方向前进104m至B处,测得仰角为60°,若学生的身高忽略不计,≈1.7,结果精确到1m,则该塔的高度CD为( )
A.81m B.85m C.88m D.93m
22.如图,小明想要测量学校操场上旗杆AB的高度,他做了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;(2)量得测角仪的高度CD=1.2米;(3)量得测角仪到旗杆的水平距离DB=m米.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.(1.2+)米 B.(1.2+)米
C.(1.2+m sinα)米 D.(1.2+m tanα)米
23.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα B.2tanα C.2cosα D.
8.如图,两条宽度均为60m的公路相交成α角,那么这两条公路在相交处的公共部分(图中阴影部分)的路面面积是( )
A.(m2) B.(m2)
C.3600sinα(m2) D.3600cosα(m2)
25.直升飞机在离地面2000米的上空测得上海东方明珠底部的俯角为30°,此时直升飞机与上海东方明珠底部之间的距离是( )
A.2000米 B.米 C.4000米 D.米
26.从一艘船上测得海岸上高为42米的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )A.42米 B.14米 C.21米 D.42米
27.如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角α为30°,则A,B两地之间的距离为( )
A.400米 B.米 C.1600米 D.800米
28.跳伞运动员小李在200米的空中测得地面上的着落点A的俯角为60°,那么此时小李离着落点A的距离是( )
A.200米 B.400米 C.米 D.米
29.如图,某同学在楼房的A处测得荷塘的一端B处的俯角为30°,荷塘另一端点D与点C,B在同一直线上,已知楼房AC=32米,CD=16米,则荷塘的宽BD为 米.
30.为了测量教学楼的高度,某同学先在点D处用测角仪测得楼顶M的仰角为30°,再沿DF方向前行40米到达点E处,在点E处测得楼顶M的仰角为45°,已知测角仪的高AD为1.5米,则此楼MF的高为 米.(结果精确到0.1米,≈1.414,≈1.732,≈2.449)
31.某校数学社团的同学对天心阁的高度进行了测量,如图,他们在A处仰望楼顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,≈1.7,结果精确到1m,则该楼的高度CD为 .
32.如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,通过测量可知河的宽度CD为50m.现需从山顶A到河对岸点C拉一条笔直的缆绳AC,则AC= m(计算结果用含根号的式子表示).
33.近年来,无人机航拍测量的应用越来越广泛.如图,拍无人机从A处观测得某建筑物顶点O时俯角为30°,继续水平前行10米到达B处,测得俯角为45°,已知无人机的水平飞行高度为45米,则这栋楼的高度是多少米?(结果保留根号)
五.解直角三角形的应用-方向角问题
34.如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AP=6千米,则A,B两点的距离为( )千米.
A.4 B.4 C.2 D.6
35.如图,一艘海轮位于灯塔P的北偏东55°方向的A处,已知PA=6海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.6海里 B.6cos55°海里
C.6sin55°海里 D.6tan55°海里
36.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距200m,则图书馆A到公路的距离AB为( )
A.100m B.100m C.100m D.m
37.如图,为测量一段笔直自西向东的河流的河面宽度,小雅同学在南岸B处测得对岸A处一棵柳树位于北偏东60°方向,她沿着河岸向东步行60米后到达C处,此时测得柳树位于北偏东30°方向,则河面的宽度是 米.
38.如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为 海里(精确到1海里,参考数据≈1.414,≈1.732).
39.一艘船向正北方向航行,在A处时看到灯塔S在船的北偏东30°的方向上,继续航行12海里到达B处,看到灯塔S在船的北偏东60°的方向上,若继续沿正北方向航行,求航行过程中船距灯塔S的最近距离.(结果精确到0.1海里)(参考数据:≈1.41,≈1.73)
参考答案
一.解直角三角形
1.解:∠A+∠ABD=∠ABD+∠DBC=90°,
∴∠A=∠DBC.
在Rt△ABD中,
sinA=,
在Rt△ABC中,
sinA=,
在Rt△CBD中,
sin∠DBC=,
故选:C.
2.解:过点C(2,1)作CD⊥x轴于D,如图所示:
则OD=2,CD=1,
在Rt△OCD中,tanα==;
故选:B.
3.解:如图所示,在Rt△ABD中,
tanB==.
故选:A.
4.解:如图,作AD⊥BC于D点.
则CD=5cm,
AB=AC=13cm.
∴底角的余弦=.
故选:A.
5.解:(1)∵∠CBD=∠A+∠ACB,∠A=45°,∠CBD=75°,
∴∠ACB=75°﹣45°=30°.
(2)如图,过点B作BH⊥AC于H.
∵∠BHA=90°,AB=60m,∠A=45°,
∴BH=AB sin45°=60(m),
∵∠BCH=30°,
∴BC=2BH=120(m).
6.解:过点C作CD⊥AB,
在Rt△CDB中,
∵sinB==,
设CD=4x,BC=5x,
则BD=3x,
∴AD=10﹣3x,
在Rt△CDA中,由勾股定理得,
AC2=AD2+CD2,
即102=(10﹣3x)2+(4x)2,
整理得:25x2﹣60x=0,
解得:x=2.4或x=0(舍去),
∴CD=4x=9.6,
在Rt△CDA中,
sinA===.
7.解:∵tanC===,
∴CD=4.
∴BD=12﹣4=8.
在Rt△ABD中,
AB=
=10.
∴cosB==.
8.解:在Rt△ABC中,∠C=90°,a=8,∠B=60°,
∴∠A=90°﹣∠B=90°﹣60°=30°,
∴c=2a=16,
∴b==8.
9.解:∵∠ACB=90°,BC=3,AC=4,
∴AB=5,
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠ACD=∠B,∠BCD=∠A,
∴sin∠ACD=sinB==,
tan∠BCD=tanA==.
二.解直角三角形的应用
10.解:在Rt△ABC中,∵∠A=90°,BC=3.5米,∠BCA=29°,
∴AB=BC sin∠ACB=3.5 sin29°,
故选:A.
11.解:∵∠ABC=90°,∠ACB=60°,BC=6m,
∴cos50°==,
∴AC=.
故选:B.
12.解:如图,过点A作AD⊥BC于点D,
∴∠BAD=∠ABD=45°,∠ACD=30,
在Rt△ABD中,BD=AD=20米,
在Rt△ADC中,DC=AD=20(米),
∴BC=BD+DC=(20+20)米.
答:BC之间的距离为(20+20)米.
13.解:在Rt△AMD中,∠MAD=45°,
∴DM=AM tan45°=2(m),
在Rt△BMC中,∠MBC=30°,
∴CM=BM tan30°,
∵BM=AM+AB=2+4=6(m),
∴CM=6×≈3.46(m),
∴CD=CM﹣DM=3.46﹣2≈1.5(米),
答:警示牌的高CD为1.5米.
14.解:(1)在Rt△ACD 中,,
∴,
在Rt△ABD 中,,
∴.
∴BC=BD﹣CD=20(m);
∴B,C 两点间的距离为BD﹣CD=20(m);
(2)此轿车的速度,
所以此轿车在该路段没有超速.
三.解直角三角形的应用-坡度坡角问题
15.解:∵河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,
∴=,
则AC=4(m),
故AB===4(m).
故选:C.
16.解:迎水坡AB的坡比是1:,即tan∠A=,
则,
又∵BC=2米,
∴AC=BC=2(米).
故选:B.
17.解:∵在离地面高度5m处引拉线固定电线杆,拉线和地面成60°角,
∴CD⊥AB且CD=5,∠A=∠B=60°,
∴AC===.
故选:B.
18.解:∵坡比为2:5,BC=30m,
∴=,即=,
解得:AC=75,
故答案为:75m.
19.解:∵AB坡度i=1:1.7,
∴AC:BC=1:1.7,
∵BC=615米,
∴AC=≈362(米),
故答案为:362.
20.解:∵迎水坡AB的坡比是1:,坝高BC=10m,
∴==,
解得:AC=10,
则AB==20(m).
故答案为:20.
四.解直角三角形的应用-仰角俯角问题
21.解:根据题意得:∠A=30°,∠DBC=60°,DC⊥AC,
∴∠ADB=∠DBC﹣∠A=30°,
∴∠ADB=∠A=30°,
∴BD=AB=104m,
∴CD=BD sin60°=104×=52≈88(m),
解法二:根据AC=CD,BC=CD,然后长度一减得到AB,再根据AB为104,可求CD.故选:C.
22.解:过C作CF⊥AB于F,则四边形BFCD是矩形,
∴BF=CD=1.2米,CF=BD=m米,
∵∠ACF=α,
∴tanα==,
∴AF=m tanα,
∴AB=BF+AF=(1.2+mtanα)(米),
即旗杆的高度为(1.2+mtanα)米,故选:D.
23.解:∵BC⊥AC,AC=2,∠BAC=α,
∴tanα=,
∴BC=AC tanα=2tanα,
故选:B.
24.解:如图,α的对边AC即为路宽60米,
即sinα=,
即斜边=,
又∵这两条公路在相交处的公共部分(图中阴影部分)是菱形,
∴路面面积=底边×高=×60=.
故选:A.
25.解:根据题意得:直升飞机与上海东方明珠底部之间的距离是 ==4000米.
故选:C.
26.解:根据题意可得:船离海岸线的距离为42÷tan30°=42(米)
故选:A.
27.解:根据题意可知:
CA⊥AB,AC=800,∠B=30°,
∴AB==800(米).
答:A,B两地之间的距离为800米.
故选:D.
28.解:根据题意,此时小李离着落点A的距离是=,
故选:D.
29.解:由题意知,∠ABC=30°,∠ACB=90°,AC=32米,
∵tan∠ABC=tan30°=,
∴BC===32(米),
∵CD=16米,
∴BD=BC﹣CD=(32﹣16)(米).
答:荷塘的宽BD为(32﹣16)米,
故答案为:(32﹣16).
30.解:在Rt△MBC中,
∵∠MBC=45°,
∴MC=BC,
在Rt△MAC中,
∵∠MAC=30°,
∴AC=MC,
设MC=x,则AC=x=40+x,
解得x=20+20≈54.64(米)
∴MF=MC+CF=54.64+1.5≈56.1(米),
故答案为:56.1.
31.解:根据题意得:∠A=30°,∠DBC=60°,DC⊥AC,
∴∠ADB=∠DBC﹣∠A=30°,
∴∠ADB=∠A=30°,
∴BD=AB=60m,
∴CD=BD sin60°=60×=30≈51(m).
故答案为51m.
32.解:作AB⊥CD交CD的延长线于点B,
在Rt△ABC中,
∵∠ACB=∠CAE=30°,∠ADB=∠EAD=45°,
∴AC=2AB,DB=AB.
设AB=x,则BD=x,AC=2x,CB=50+x,
∵tan∠ACB=tan30°,
∴AB=CB tan∠ACB=CB tan30°.
∴x=(50+x) .
解得:x=25(1+),
∴AC=50(1+)(米).
答:缆绳AC的长为50(1+)米.
故答案为:50(1+)
33.解:过O点作OC⊥AB的延长线于C点,垂足为C,
根据题意可知,∠OAC=30°,∠OBC=45°,AB=10米,AD=45米,
在Rt△BCO中,∠OBC=45°,
∴BC=OC,
设OC=BC=x,则AC=10+x,
在Rt△ACO中,
tan30°===,
解得x=5+5,
则这栋楼的高度h=AD﹣CO=45﹣5﹣5=(40﹣5)(米).
五.解直角三角形的应用-方向角问题
34.解:由题意知,∠PAB=30°,∠PBC=60°,
∴∠APB=∠PBC﹣∠PAB=60°﹣30°=30°,
∴∠PAB=∠APB,
∴AB=PB,
在Rt△PAC中,∵AP=6千米,
∴PC=PA=3千米,
在Rt△PBC中,∵sin∠PBC=,
∴PB===6千米.
故选:D.
35.解:如图所示:
由题意可知∠NPA=55°,PA=6海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=55°.
在Rt△ABP中,∵∠ABP=90°,∠A=55°,PA=6海里,
∴AB=AP cos∠A=6cos55°海里.
故选:B.
36.解:由题意得,∠AOB=90°﹣60°=30°,
∴AB=OA=100(m),
故选:A.
37.解:如图,过A作AD⊥BC于D,
由题意可知:BC=60米,∠ABD=30°,∠ACD=60°,
∴∠BAC=∠ACD﹣∠ABC=30°,
∴∠ABC=∠BAC,
∴BC=AC=60(米).
在Rt△ACD中,AD=AC sin60°=60×=30(米).
即这条河的宽度为30米,
故答案为:30.
38.解:根据题意可知:
AB=30×(10﹣8)=60(海里),∠ACD=45°,∠BCD=30°,
如图,作CD⊥AB于点D,
在Rt△ACD中,CD=AD,
在Rt△CBD中,BD=AB﹣AD=60﹣CD,
∴tan30°=,
即=,
解得CD≈38(海里).
经检验CD≈38是原分式方程的解.
答:轮船在航行中离小岛最近的距离约为38海里.故答案为:38.
39.解:过S作SC⊥AB于C.
∵∠SBC=60°,∠A=30°,
∴∠BSA=∠SBC﹣∠A=30°,
即∠BSA=∠A=30°.
∴SB=AB=12(海里).
Rt△BCS中,BS=12,∠SBC=60°,
∴SC=SB sin60°=12×=6≈10.4(海里).
答:船继续沿正北方向航行过程中距灯塔S的最近距离是10.4海里
题型分类训练(附答案)
一.解直角三角形
1.如图,∠ABC=∠BDA=90°,下列线段比值等于sinA的是( )
A. B. C. D.
2.如图,在平面直角坐标系xOy中,直线OA过点(2,1),直线OA与x轴的夹角为α,则tanα的值为( )
A. B. C.2 D.
3.如图,A,B,C是3×1的正方形网格中的三个格点,则tanB的值为( )
A. B. C. D.
4.等腰三角形底边长为10cm,周长为36cm,那么底角的余弦等于( )
A. B. C. D.
5.如图,A、B、D三点在同一水平线上,CD⊥AD,∠A=45°,∠CBD=75°,AB=60m.
(1)求∠ACB的度数;
(2)求线段CB的长度.
6.如图,在△ABC中,AB=AC=10,.求sinA的值.
7.如图,在△ABC中,AD⊥BC于点D,若AD=6.tanC=,BC=12,求cosB的值.
8.根据下列条件,解直角三角形:在Rt△ABC中,∠C=90°,a=8,∠B=60°.
9.如图,在△ABC中,∠ACB=90°,BC=3,AC=4,CD⊥AB,垂足为D,求sin∠ACD和tan∠BCD.
二.解直角三角形的应用
10.某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
A.3.5sin29° B.3.5cos29° C.3.5tan29° D.
11.如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
A. B. C.6cos50° D.
12.学校进行实践活动,喜欢数学的小伟沿笔直的河岸BC进行数学实践活动,如图,河对岸有一码头A,小伟在河岸B处测得∠ABC=45°,沿河岸到达C处,在C处测得∠ACB=30,已知河宽为20米,求B、C之间的距离.
13.如图,某景区门口的柱子上方挂着一块景点宣传牌CD,宣传牌的一侧用绳子AD和BC牵引着两排小风车,经过测量得到如下数据:AM=2米,AB=4米,∠MAD=45°,∠MBC=30°,则CD的长度约为 米.(≈1.73,结果精确到0.1米)
14.如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.(参考数据:tan31°≈0.6,tan50°≈1.2)
(1)求B,C两点间的距离(结果精确到1m);
(2)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
三.解直角三角形的应用-坡度坡角问题
15.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,则AB的长度为( )
A.2m B.4m C.4m D.6m
16.如图,河堤横断面迎水坡AB的坡比是1:,堤高BC=2米,则迎水坡宽度AC的长为( )
A.4米 B.2米 C.米 D.2米
17.如图,在离地面高度5m处引拉线固定电线杆,拉线和地面成60°角,则拉线AC的长是( )
A.10m B.m C.m D.5m
18.有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若坡比为2:5,则此斜坡的水平距离AC为 .
19.钓鱼岛是中国固有领土,2021年4月26日,国家自然资源部发布了钓鱼岛地形地貌调查报告,钓鱼岛中央山脊呈东西走向,北坡稍缓,南坡陡峭,已知主峰高华峰北坡AB坡度i=1:1.7,海平面上BC的水平距离约为615米,则主峰高华峰的高度AC约为 米.(精确到1米)
20.拦水坝横断面如图所示,迎水坡AB的坡比是1:,坝高BC=10m,则坡面AB的长度是 m.
四.解直角三角形的应用-仰角俯角问题
21.长沙电视塔位于岳麓山顶峰,其功能集广播电视信号发射与旅游观光于一身某校数学社团的同学对长沙电视塔的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往塔的方向前进104m至B处,测得仰角为60°,若学生的身高忽略不计,≈1.7,结果精确到1m,则该塔的高度CD为( )
A.81m B.85m C.88m D.93m
22.如图,小明想要测量学校操场上旗杆AB的高度,他做了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;(2)量得测角仪的高度CD=1.2米;(3)量得测角仪到旗杆的水平距离DB=m米.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.(1.2+)米 B.(1.2+)米
C.(1.2+m sinα)米 D.(1.2+m tanα)米
23.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα B.2tanα C.2cosα D.
8.如图,两条宽度均为60m的公路相交成α角,那么这两条公路在相交处的公共部分(图中阴影部分)的路面面积是( )
A.(m2) B.(m2)
C.3600sinα(m2) D.3600cosα(m2)
25.直升飞机在离地面2000米的上空测得上海东方明珠底部的俯角为30°,此时直升飞机与上海东方明珠底部之间的距离是( )
A.2000米 B.米 C.4000米 D.米
26.从一艘船上测得海岸上高为42米的灯塔顶部的仰角为30°时,船离灯塔的水平距离是( )A.42米 B.14米 C.21米 D.42米
27.如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上).为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角α为30°,则A,B两地之间的距离为( )
A.400米 B.米 C.1600米 D.800米
28.跳伞运动员小李在200米的空中测得地面上的着落点A的俯角为60°,那么此时小李离着落点A的距离是( )
A.200米 B.400米 C.米 D.米
29.如图,某同学在楼房的A处测得荷塘的一端B处的俯角为30°,荷塘另一端点D与点C,B在同一直线上,已知楼房AC=32米,CD=16米,则荷塘的宽BD为 米.
30.为了测量教学楼的高度,某同学先在点D处用测角仪测得楼顶M的仰角为30°,再沿DF方向前行40米到达点E处,在点E处测得楼顶M的仰角为45°,已知测角仪的高AD为1.5米,则此楼MF的高为 米.(结果精确到0.1米,≈1.414,≈1.732,≈2.449)
31.某校数学社团的同学对天心阁的高度进行了测量,如图,他们在A处仰望楼顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计,≈1.7,结果精确到1m,则该楼的高度CD为 .
32.如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,通过测量可知河的宽度CD为50m.现需从山顶A到河对岸点C拉一条笔直的缆绳AC,则AC= m(计算结果用含根号的式子表示).
33.近年来,无人机航拍测量的应用越来越广泛.如图,拍无人机从A处观测得某建筑物顶点O时俯角为30°,继续水平前行10米到达B处,测得俯角为45°,已知无人机的水平飞行高度为45米,则这栋楼的高度是多少米?(结果保留根号)
五.解直角三角形的应用-方向角问题
34.如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AP=6千米,则A,B两点的距离为( )千米.
A.4 B.4 C.2 D.6
35.如图,一艘海轮位于灯塔P的北偏东55°方向的A处,已知PA=6海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.6海里 B.6cos55°海里
C.6sin55°海里 D.6tan55°海里
36.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距200m,则图书馆A到公路的距离AB为( )
A.100m B.100m C.100m D.m
37.如图,为测量一段笔直自西向东的河流的河面宽度,小雅同学在南岸B处测得对岸A处一棵柳树位于北偏东60°方向,她沿着河岸向东步行60米后到达C处,此时测得柳树位于北偏东30°方向,则河面的宽度是 米.
38.如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为 海里(精确到1海里,参考数据≈1.414,≈1.732).
39.一艘船向正北方向航行,在A处时看到灯塔S在船的北偏东30°的方向上,继续航行12海里到达B处,看到灯塔S在船的北偏东60°的方向上,若继续沿正北方向航行,求航行过程中船距灯塔S的最近距离.(结果精确到0.1海里)(参考数据:≈1.41,≈1.73)
参考答案
一.解直角三角形
1.解:∠A+∠ABD=∠ABD+∠DBC=90°,
∴∠A=∠DBC.
在Rt△ABD中,
sinA=,
在Rt△ABC中,
sinA=,
在Rt△CBD中,
sin∠DBC=,
故选:C.
2.解:过点C(2,1)作CD⊥x轴于D,如图所示:
则OD=2,CD=1,
在Rt△OCD中,tanα==;
故选:B.
3.解:如图所示,在Rt△ABD中,
tanB==.
故选:A.
4.解:如图,作AD⊥BC于D点.
则CD=5cm,
AB=AC=13cm.
∴底角的余弦=.
故选:A.
5.解:(1)∵∠CBD=∠A+∠ACB,∠A=45°,∠CBD=75°,
∴∠ACB=75°﹣45°=30°.
(2)如图,过点B作BH⊥AC于H.
∵∠BHA=90°,AB=60m,∠A=45°,
∴BH=AB sin45°=60(m),
∵∠BCH=30°,
∴BC=2BH=120(m).
6.解:过点C作CD⊥AB,
在Rt△CDB中,
∵sinB==,
设CD=4x,BC=5x,
则BD=3x,
∴AD=10﹣3x,
在Rt△CDA中,由勾股定理得,
AC2=AD2+CD2,
即102=(10﹣3x)2+(4x)2,
整理得:25x2﹣60x=0,
解得:x=2.4或x=0(舍去),
∴CD=4x=9.6,
在Rt△CDA中,
sinA===.
7.解:∵tanC===,
∴CD=4.
∴BD=12﹣4=8.
在Rt△ABD中,
AB=
=10.
∴cosB==.
8.解:在Rt△ABC中,∠C=90°,a=8,∠B=60°,
∴∠A=90°﹣∠B=90°﹣60°=30°,
∴c=2a=16,
∴b==8.
9.解:∵∠ACB=90°,BC=3,AC=4,
∴AB=5,
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠ACD=∠B,∠BCD=∠A,
∴sin∠ACD=sinB==,
tan∠BCD=tanA==.
二.解直角三角形的应用
10.解:在Rt△ABC中,∵∠A=90°,BC=3.5米,∠BCA=29°,
∴AB=BC sin∠ACB=3.5 sin29°,
故选:A.
11.解:∵∠ABC=90°,∠ACB=60°,BC=6m,
∴cos50°==,
∴AC=.
故选:B.
12.解:如图,过点A作AD⊥BC于点D,
∴∠BAD=∠ABD=45°,∠ACD=30,
在Rt△ABD中,BD=AD=20米,
在Rt△ADC中,DC=AD=20(米),
∴BC=BD+DC=(20+20)米.
答:BC之间的距离为(20+20)米.
13.解:在Rt△AMD中,∠MAD=45°,
∴DM=AM tan45°=2(m),
在Rt△BMC中,∠MBC=30°,
∴CM=BM tan30°,
∵BM=AM+AB=2+4=6(m),
∴CM=6×≈3.46(m),
∴CD=CM﹣DM=3.46﹣2≈1.5(米),
答:警示牌的高CD为1.5米.
14.解:(1)在Rt△ACD 中,,
∴,
在Rt△ABD 中,,
∴.
∴BC=BD﹣CD=20(m);
∴B,C 两点间的距离为BD﹣CD=20(m);
(2)此轿车的速度,
所以此轿车在该路段没有超速.
三.解直角三角形的应用-坡度坡角问题
15.解:∵河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,
∴=,
则AC=4(m),
故AB===4(m).
故选:C.
16.解:迎水坡AB的坡比是1:,即tan∠A=,
则,
又∵BC=2米,
∴AC=BC=2(米).
故选:B.
17.解:∵在离地面高度5m处引拉线固定电线杆,拉线和地面成60°角,
∴CD⊥AB且CD=5,∠A=∠B=60°,
∴AC===.
故选:B.
18.解:∵坡比为2:5,BC=30m,
∴=,即=,
解得:AC=75,
故答案为:75m.
19.解:∵AB坡度i=1:1.7,
∴AC:BC=1:1.7,
∵BC=615米,
∴AC=≈362(米),
故答案为:362.
20.解:∵迎水坡AB的坡比是1:,坝高BC=10m,
∴==,
解得:AC=10,
则AB==20(m).
故答案为:20.
四.解直角三角形的应用-仰角俯角问题
21.解:根据题意得:∠A=30°,∠DBC=60°,DC⊥AC,
∴∠ADB=∠DBC﹣∠A=30°,
∴∠ADB=∠A=30°,
∴BD=AB=104m,
∴CD=BD sin60°=104×=52≈88(m),
解法二:根据AC=CD,BC=CD,然后长度一减得到AB,再根据AB为104,可求CD.故选:C.
22.解:过C作CF⊥AB于F,则四边形BFCD是矩形,
∴BF=CD=1.2米,CF=BD=m米,
∵∠ACF=α,
∴tanα==,
∴AF=m tanα,
∴AB=BF+AF=(1.2+mtanα)(米),
即旗杆的高度为(1.2+mtanα)米,故选:D.
23.解:∵BC⊥AC,AC=2,∠BAC=α,
∴tanα=,
∴BC=AC tanα=2tanα,
故选:B.
24.解:如图,α的对边AC即为路宽60米,
即sinα=,
即斜边=,
又∵这两条公路在相交处的公共部分(图中阴影部分)是菱形,
∴路面面积=底边×高=×60=.
故选:A.
25.解:根据题意得:直升飞机与上海东方明珠底部之间的距离是 ==4000米.
故选:C.
26.解:根据题意可得:船离海岸线的距离为42÷tan30°=42(米)
故选:A.
27.解:根据题意可知:
CA⊥AB,AC=800,∠B=30°,
∴AB==800(米).
答:A,B两地之间的距离为800米.
故选:D.
28.解:根据题意,此时小李离着落点A的距离是=,
故选:D.
29.解:由题意知,∠ABC=30°,∠ACB=90°,AC=32米,
∵tan∠ABC=tan30°=,
∴BC===32(米),
∵CD=16米,
∴BD=BC﹣CD=(32﹣16)(米).
答:荷塘的宽BD为(32﹣16)米,
故答案为:(32﹣16).
30.解:在Rt△MBC中,
∵∠MBC=45°,
∴MC=BC,
在Rt△MAC中,
∵∠MAC=30°,
∴AC=MC,
设MC=x,则AC=x=40+x,
解得x=20+20≈54.64(米)
∴MF=MC+CF=54.64+1.5≈56.1(米),
故答案为:56.1.
31.解:根据题意得:∠A=30°,∠DBC=60°,DC⊥AC,
∴∠ADB=∠DBC﹣∠A=30°,
∴∠ADB=∠A=30°,
∴BD=AB=60m,
∴CD=BD sin60°=60×=30≈51(m).
故答案为51m.
32.解:作AB⊥CD交CD的延长线于点B,
在Rt△ABC中,
∵∠ACB=∠CAE=30°,∠ADB=∠EAD=45°,
∴AC=2AB,DB=AB.
设AB=x,则BD=x,AC=2x,CB=50+x,
∵tan∠ACB=tan30°,
∴AB=CB tan∠ACB=CB tan30°.
∴x=(50+x) .
解得:x=25(1+),
∴AC=50(1+)(米).
答:缆绳AC的长为50(1+)米.
故答案为:50(1+)
33.解:过O点作OC⊥AB的延长线于C点,垂足为C,
根据题意可知,∠OAC=30°,∠OBC=45°,AB=10米,AD=45米,
在Rt△BCO中,∠OBC=45°,
∴BC=OC,
设OC=BC=x,则AC=10+x,
在Rt△ACO中,
tan30°===,
解得x=5+5,
则这栋楼的高度h=AD﹣CO=45﹣5﹣5=(40﹣5)(米).
五.解直角三角形的应用-方向角问题
34.解:由题意知,∠PAB=30°,∠PBC=60°,
∴∠APB=∠PBC﹣∠PAB=60°﹣30°=30°,
∴∠PAB=∠APB,
∴AB=PB,
在Rt△PAC中,∵AP=6千米,
∴PC=PA=3千米,
在Rt△PBC中,∵sin∠PBC=,
∴PB===6千米.
故选:D.
35.解:如图所示:
由题意可知∠NPA=55°,PA=6海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=55°.
在Rt△ABP中,∵∠ABP=90°,∠A=55°,PA=6海里,
∴AB=AP cos∠A=6cos55°海里.
故选:B.
36.解:由题意得,∠AOB=90°﹣60°=30°,
∴AB=OA=100(m),
故选:A.
37.解:如图,过A作AD⊥BC于D,
由题意可知:BC=60米,∠ABD=30°,∠ACD=60°,
∴∠BAC=∠ACD﹣∠ABC=30°,
∴∠ABC=∠BAC,
∴BC=AC=60(米).
在Rt△ACD中,AD=AC sin60°=60×=30(米).
即这条河的宽度为30米,
故答案为:30.
38.解:根据题意可知:
AB=30×(10﹣8)=60(海里),∠ACD=45°,∠BCD=30°,
如图,作CD⊥AB于点D,
在Rt△ACD中,CD=AD,
在Rt△CBD中,BD=AB﹣AD=60﹣CD,
∴tan30°=,
即=,
解得CD≈38(海里).
经检验CD≈38是原分式方程的解.
答:轮船在航行中离小岛最近的距离约为38海里.故答案为:38.
39.解:过S作SC⊥AB于C.
∵∠SBC=60°,∠A=30°,
∴∠BSA=∠SBC﹣∠A=30°,
即∠BSA=∠A=30°.
∴SB=AB=12(海里).
Rt△BCS中,BS=12,∠SBC=60°,
∴SC=SB sin60°=12×=6≈10.4(海里).
答:船继续沿正北方向航行过程中距灯塔S的最近距离是10.4海里
