2021-2022学年冀教版八年级上学期期末数学复习试卷(Word版含解析)
文档属性
| 名称 | 2021-2022学年冀教版八年级上学期期末数学复习试卷(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 284.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 15:38:33 | ||
图片预览




文档简介
2021-2022学年冀教新版八年级上册数学期末复习试卷
一.选择题(共14小题,满分42分,每小题3分)
1.下列命题中,是真命题的是( )
A.在同一平面内,垂直于同一直线的两条直线平行
B.相等的角是对顶角
C.两条直线被第三条直线所截,同旁内角互补
D.过一点有且只有一条直线与已知直线平行
2.用四舍五入法按要求对0.05095分别取近似值,其中错误的是( )
A.0.1(精确到0.1) B.0.05(精确到百分位)
C.0.051(精确到千分位) D.0.0510(精确到0.001)
3.若分式在实数范围内有意义,则x的取值范围是( )
A.x≠﹣5 B.x≠0 C.x≠5 D.x>﹣5
4.下列正方体的表面展开图中,是中心对称图形的是( )
A. B. C. D.
5.无论x取任何实数,下列一定是二次根式的是( )
A. B. C. D.
6.计算,结果正确的是( )
A.4 B.10 C.2 D.
7.计算+的结果是( )
A.﹣1 B.2x﹣5 C.5﹣2x D.1
8.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3 B.4 C.5 D.6
9.等腰三角形两边长分别为3,7,则它的周长为( )
A.13 B.17 C.13或17 D.不能确定
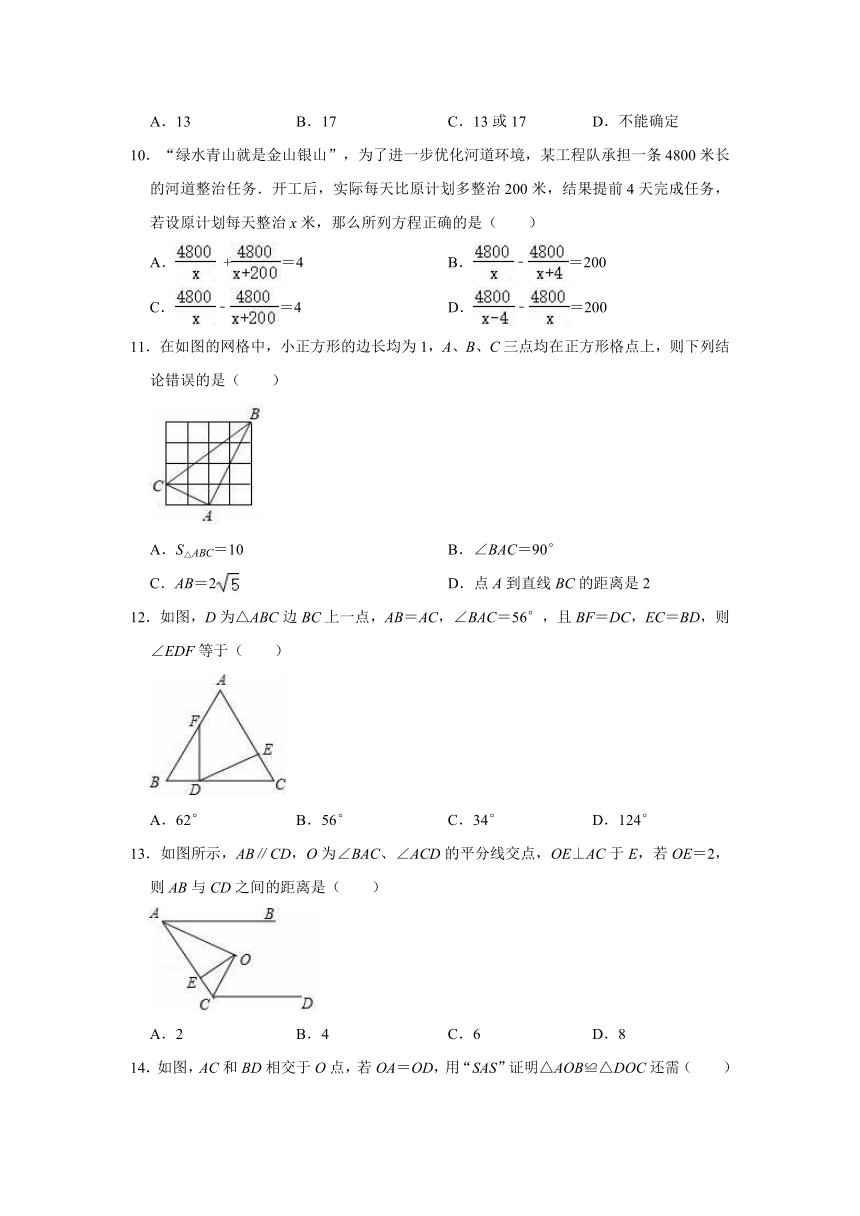
10.“绿水青山就是金山银山”,为了进一步优化河道环境,某工程队承担一条4800米长的河道整治任务.开工后,实际每天比原计划多整治200米,结果提前4天完成任务,若设原计划每天整治x米,那么所列方程正确的是( )
A. +=4 B.﹣=200
C.﹣=4 D.﹣=200
11.在如图的网格中,小正方形的边长均为1,A、B、C三点均在正方形格点上,则下列结论错误的是( )
A.S△ABC=10 B.∠BAC=90°
C.AB=2 D.点A到直线BC的距离是2
12.如图,D为△ABC边BC上一点,AB=AC,∠BAC=56°,且BF=DC,EC=BD,则∠EDF等于( )
A.62° B.56° C.34° D.124°
13.如图所示,AB∥CD,O为∠BAC、∠ACD的平分线交点,OE⊥AC于E,若OE=2,则AB与CD之间的距离是( )
A.2 B.4 C.6 D.8
14.如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( )
A.AB=DC B.OB=OC C.∠C=∠D D.∠AOB=∠DOC
二.填空题(共6小题,满分18分,每小题3分)
15.16的算术平方根是 .
16.如果一个正数的平方根是a+3和2a﹣15,则这个数为 .
17.下列说法:①无理数就是开方开不尽的数;②满足﹣<x<的x的整数有4个;③﹣3是的一个平方根;④不带根号的数都是有理数;⑤不是有限小数的不是有理数;⑥对于任意实数a,都有=a.其中正确的序号是 .
18.计算: += .
19.如图,等腰三角形ABC底边BC的长为4cm,面积是12cm2,D为BC边上的中点,腰AB的垂直平分线EF交AD于M,交AC于点F,则BM+DM的值为 cm.
20.在四边形ABCD中,∠A=∠ABC=90°,△BCD为等边三角形,且AD=2,则四边形ABCD的周长为 .
三.解答题(共6小题,满分60分,每小题10分)
21.计算:
(1).
(2).
22.如图,在△ABC中,∠A=40°,∠B=80°.
(1)请用尺规作图在平面内确定一点O,使得点O到AC、BC两边的距离相等,且点O到A,B两点的距离也相等;(保留作图痕迹,不写作法)
(2)若OC=6,求点O到BC的距离.
23.计算: +÷.
24.如图,在树上距地面10m的D处有两只猴子,它们同时发现地面上C处有一筐水果,一只猴子从D处向上爬到树顶A处,然后利用拉在A处的滑绳AC滑到C处,另一只猴子从D处先滑到地面B,再由B跑到C,已知两猴子所经过的路程都是15m,求树高AB.
25.如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,这两条垂直平分线分别交BC于点D、E.已知△ADE的周长为13cm.
(1)求线段BC;
(2)分别连接OA、OB、OC,若△OBC的周长为27cm,则OA的长为 cm.
26.已知:如图,在△ABC中,D是BC的中点,点E、F分别在AB、AC上,且DE∥AC,DF∥AB,求证:BE=DF,DE=CF.
参考答案与试题解析
一.选择题(共14小题,满分42分,每小题3分)
1.解:A、在同一平面内,垂直于同一直线的两条直线平行,是真命题;
B、相等的角不一定是对顶角,是假命题;
C、两条平行线被第三条直线所截,同旁内角互补,是假命题;
D、过直线外一点有且只有一条直线与已知直线平行,是假命题;
故选:A.
2.解:A、0.1(精确到0.1),正确;
B、0.05(精确到百分位),正确;
C、0.051(精确到千分位),正确;
D、0.0510(精确到0.0001),故本选项错误;
故选:D.
3.解:根据分式成立的条件,可得:x+5≠0,
∴x≠﹣5,
故选:A.
4.解:A、不是中心对称图形,本选项错误;
B、不是中心对称图形,本选项错误;
C、不是中心对称图形,本选项错误;
D、是中心对称图形,本选项正确.
故选:D.
5.解:A、,根号下部分有可能小于零,故此选项错误;
B、,根号下部分有可能小于零,故此选项错误;
C、,根号下部分不可能小于零,故此选项正确;
D、,根号下部分有可能小于零,故此选项错误.
故选:C.
6.解:原式=+3
=4.
故选:A.
7.解:由题意得,2﹣x≥0,
解得,x≤2,
原式=2﹣x+|x﹣3|
=2﹣x﹣(x﹣3)
=2﹣x﹣x+3
=5﹣2x,
故选:C.
8.解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=AB DE=×10 DE=15,
解得DE=3,
∴CD=3.
故选:A.
9.解:当相等的两边是3时,3+3<7,不能组成三角形,应舍去;
当相等的两边是7时,能够组成三角形,此时周长是7+7+3=17.
故选:B.
10.解:设原计划每天挖x米,则原计划用时为:天,实际用时为:天.
所列方程为:﹣=4,
故选:C.
11.解:A、S△ABC=4×4﹣×3×4﹣×1×2﹣×2×4=5,本选项结论错误,符合题意;
B、∵AC2=12+22=5,AB2=22+42=20,BC2=32+42=25,
∴AC2+AB2=BC2,
∴∠BAC=90°,本选项结论正确,不符合题意;
C、∵AB2=20,
∴AB=2,本选项结论正确,不符合题意;
D、设点A到直线BC的距离为h,
则××2=×5×h,
解得,h=2,本选项结论正确,不符合题意;
故选:A.
12.解:∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=(180°﹣56°)=62°,
在△BFD和△EDC中,,
∴△BFD≌△EDC(SAS),
∴∠BFD=∠EDC,
∴∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=180°﹣62°=118°,
则∠EDF=180°﹣(∠FDB+∠EDC)=180°﹣118°=62°.
故选:A.
13.解:如图,过点O作MN,MN⊥AB于M,交CD于N,
∵AB∥CD,
∴MN⊥CD,
∵AO是∠BAC的平分线,OM⊥AB,OE⊥AC,OE=2,
∴OM=OE=2,
∵CO是∠ACD的平分线,OE⊥AC,ON⊥CD,
∴ON=OE=2,
∴MN=OM+ON=4,
即AB与CD之间的距离是4.
故选:B.
14.解:A、AB=DC,不能根据SAS证两三角形全等,故本选项错误;
B、∵在△AOB和△DOC中
,
∴△AOB≌△DOC(SAS),故本选项正确;
C、两三角形相等的条件只有OA=OD和∠AOB=∠DOC,不能证两三角形全等,故本选项错误;
D、根据∠AOB=∠DOC和OA=OD,不能证两三角形全等,故本选项错误;
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
15.解:∵42=16,
∴=4.
故答案为:4.
16.解:∵一个正数的平方根是a+3和2a﹣15,
∴a+3和2a﹣15互为相反数,
即(a+3)+(2a﹣15)=0;
解得a=4,
则a+3=﹣(2a﹣15)=7;
则这个数为72=49;
故答案为49.
17.解:①开方开不尽的数是无理数,但是有的数不开方也是无理数,如:π,等,因此①不正确,不符合题意;
②满足﹣<x<的x的整数有﹣1,0,1,2共4个,因此②正确,符合题意;
③﹣3是9的一个平方根,而=9,因此③正确,符合题意;
④π就是无理数,不带根号的数也不一定是有理数,因此④不正确,不符合题意;
⑤无限循环小数,即分数是有理数,因此⑤不正确,不符合题意;
⑥若a<0,则=|a|=﹣a,因此⑥不正确,不符合题意;
因此正确的结论有②③,
故答案为:②③.
18.解:原式=2+3=;
故答案为:5.
19.解:∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC AD=×4×AD=12,
解得AD=6(cm),
∵EF是线段AB的垂直平分线,
∴AM=BM,
∴BM+MD=AM+DM=AD=6(cm),
故答案为:6.
20.解:∵△BCD为等边三角形,
∴∠DBC=60°,DB=BC=CD,
∵∠ABC=90°,
∴∠ABD=30°,
∵在Rt△ABC中,∠ABD=30°,AD=2
∴DB=4,
∴CD=BC=4,
在Rt△ABC中,由勾股定理,得AB===2,
∴四边形ABCD的周长=AB+BC+CD+DA=2+4+4+2=2+10,
故答案为:2+10.
三.解答题(共6小题,满分60分,每小题10分)
21.解:(1)原式=3﹣5+
=﹣;
(2)原式=3﹣5+3﹣﹣2
=﹣2.
22.解:(1)如图,点O为所作;
(2)过O点作OH⊥BC于H,如图,
∵∠A=40°,∠ABC=80°,
∴∠ACB=180°﹣∠A﹣∠ABC=180°﹣40°﹣80°=60°,
∵点O到AC、BC两边的距离相等,
∴CO平分∠ACB,
∴∠OCH=30°,
∴OB=OC=×6=3,
即点O到BC的距离为3.
23.解:原式=+
=+
=
=
=.
24.解:Rt△ABC中,∠B=90°,
设BC=a(m),AC=b(m),AD=x(m)
则10+a=x+b=15(m).
∴a=5(m),b=15﹣x(m)
又在Rt△ABC中,由勾股定理得:(10+x)2+a2=b2,
∴(10+x)2+52=(15﹣x)2,
解得,x=2,即AD=2(米)
∴AB=AD+DB=2+10=12(米)
答:树高AB为12米.
25.解:(1)∵OM是线段AB的垂直平分线,
∴DA=DB,
同理,EA=EC,
∵△ADE的周长13,
∴AD+DE+EA=13,
∴BC=DB+DE+EC=AD+DE+EA=13(cm);
(2)连接OB,OC,
∵△OBC的周长为27,
∴OB+OC+BC=27,
∵BC=13,
∴OB+OC=14,
∵OM垂直平分AB,
∴OA=OB,
同理,OA=OC,
∴OA=OB=OC=7(cm),
故答案为:7.
26.证明:∵D是BC的中点,
∴BD=CD,
∵DF∥AB,
∴∠B=∠CDF,
∵DE∥AC,
∴∠C=∠BDE,
在△BDE和△DCF中,,
∴△BDE≌△DCF(ASA),
∴BE=DF,DE=CF.
一.选择题(共14小题,满分42分,每小题3分)
1.下列命题中,是真命题的是( )
A.在同一平面内,垂直于同一直线的两条直线平行
B.相等的角是对顶角
C.两条直线被第三条直线所截,同旁内角互补
D.过一点有且只有一条直线与已知直线平行
2.用四舍五入法按要求对0.05095分别取近似值,其中错误的是( )
A.0.1(精确到0.1) B.0.05(精确到百分位)
C.0.051(精确到千分位) D.0.0510(精确到0.001)
3.若分式在实数范围内有意义,则x的取值范围是( )
A.x≠﹣5 B.x≠0 C.x≠5 D.x>﹣5
4.下列正方体的表面展开图中,是中心对称图形的是( )
A. B. C. D.
5.无论x取任何实数,下列一定是二次根式的是( )
A. B. C. D.
6.计算,结果正确的是( )
A.4 B.10 C.2 D.
7.计算+的结果是( )
A.﹣1 B.2x﹣5 C.5﹣2x D.1
8.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3 B.4 C.5 D.6
9.等腰三角形两边长分别为3,7,则它的周长为( )
A.13 B.17 C.13或17 D.不能确定
10.“绿水青山就是金山银山”,为了进一步优化河道环境,某工程队承担一条4800米长的河道整治任务.开工后,实际每天比原计划多整治200米,结果提前4天完成任务,若设原计划每天整治x米,那么所列方程正确的是( )
A. +=4 B.﹣=200
C.﹣=4 D.﹣=200
11.在如图的网格中,小正方形的边长均为1,A、B、C三点均在正方形格点上,则下列结论错误的是( )
A.S△ABC=10 B.∠BAC=90°
C.AB=2 D.点A到直线BC的距离是2
12.如图,D为△ABC边BC上一点,AB=AC,∠BAC=56°,且BF=DC,EC=BD,则∠EDF等于( )
A.62° B.56° C.34° D.124°
13.如图所示,AB∥CD,O为∠BAC、∠ACD的平分线交点,OE⊥AC于E,若OE=2,则AB与CD之间的距离是( )
A.2 B.4 C.6 D.8
14.如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( )
A.AB=DC B.OB=OC C.∠C=∠D D.∠AOB=∠DOC
二.填空题(共6小题,满分18分,每小题3分)
15.16的算术平方根是 .
16.如果一个正数的平方根是a+3和2a﹣15,则这个数为 .
17.下列说法:①无理数就是开方开不尽的数;②满足﹣<x<的x的整数有4个;③﹣3是的一个平方根;④不带根号的数都是有理数;⑤不是有限小数的不是有理数;⑥对于任意实数a,都有=a.其中正确的序号是 .
18.计算: += .
19.如图,等腰三角形ABC底边BC的长为4cm,面积是12cm2,D为BC边上的中点,腰AB的垂直平分线EF交AD于M,交AC于点F,则BM+DM的值为 cm.
20.在四边形ABCD中,∠A=∠ABC=90°,△BCD为等边三角形,且AD=2,则四边形ABCD的周长为 .
三.解答题(共6小题,满分60分,每小题10分)
21.计算:
(1).
(2).
22.如图,在△ABC中,∠A=40°,∠B=80°.
(1)请用尺规作图在平面内确定一点O,使得点O到AC、BC两边的距离相等,且点O到A,B两点的距离也相等;(保留作图痕迹,不写作法)
(2)若OC=6,求点O到BC的距离.
23.计算: +÷.
24.如图,在树上距地面10m的D处有两只猴子,它们同时发现地面上C处有一筐水果,一只猴子从D处向上爬到树顶A处,然后利用拉在A处的滑绳AC滑到C处,另一只猴子从D处先滑到地面B,再由B跑到C,已知两猴子所经过的路程都是15m,求树高AB.
25.如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,这两条垂直平分线分别交BC于点D、E.已知△ADE的周长为13cm.
(1)求线段BC;
(2)分别连接OA、OB、OC,若△OBC的周长为27cm,则OA的长为 cm.
26.已知:如图,在△ABC中,D是BC的中点,点E、F分别在AB、AC上,且DE∥AC,DF∥AB,求证:BE=DF,DE=CF.
参考答案与试题解析
一.选择题(共14小题,满分42分,每小题3分)
1.解:A、在同一平面内,垂直于同一直线的两条直线平行,是真命题;
B、相等的角不一定是对顶角,是假命题;
C、两条平行线被第三条直线所截,同旁内角互补,是假命题;
D、过直线外一点有且只有一条直线与已知直线平行,是假命题;
故选:A.
2.解:A、0.1(精确到0.1),正确;
B、0.05(精确到百分位),正确;
C、0.051(精确到千分位),正确;
D、0.0510(精确到0.0001),故本选项错误;
故选:D.
3.解:根据分式成立的条件,可得:x+5≠0,
∴x≠﹣5,
故选:A.
4.解:A、不是中心对称图形,本选项错误;
B、不是中心对称图形,本选项错误;
C、不是中心对称图形,本选项错误;
D、是中心对称图形,本选项正确.
故选:D.
5.解:A、,根号下部分有可能小于零,故此选项错误;
B、,根号下部分有可能小于零,故此选项错误;
C、,根号下部分不可能小于零,故此选项正确;
D、,根号下部分有可能小于零,故此选项错误.
故选:C.
6.解:原式=+3
=4.
故选:A.
7.解:由题意得,2﹣x≥0,
解得,x≤2,
原式=2﹣x+|x﹣3|
=2﹣x﹣(x﹣3)
=2﹣x﹣x+3
=5﹣2x,
故选:C.
8.解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=AB DE=×10 DE=15,
解得DE=3,
∴CD=3.
故选:A.
9.解:当相等的两边是3时,3+3<7,不能组成三角形,应舍去;
当相等的两边是7时,能够组成三角形,此时周长是7+7+3=17.
故选:B.
10.解:设原计划每天挖x米,则原计划用时为:天,实际用时为:天.
所列方程为:﹣=4,
故选:C.
11.解:A、S△ABC=4×4﹣×3×4﹣×1×2﹣×2×4=5,本选项结论错误,符合题意;
B、∵AC2=12+22=5,AB2=22+42=20,BC2=32+42=25,
∴AC2+AB2=BC2,
∴∠BAC=90°,本选项结论正确,不符合题意;
C、∵AB2=20,
∴AB=2,本选项结论正确,不符合题意;
D、设点A到直线BC的距离为h,
则××2=×5×h,
解得,h=2,本选项结论正确,不符合题意;
故选:A.
12.解:∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=(180°﹣56°)=62°,
在△BFD和△EDC中,,
∴△BFD≌△EDC(SAS),
∴∠BFD=∠EDC,
∴∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=180°﹣62°=118°,
则∠EDF=180°﹣(∠FDB+∠EDC)=180°﹣118°=62°.
故选:A.
13.解:如图,过点O作MN,MN⊥AB于M,交CD于N,
∵AB∥CD,
∴MN⊥CD,
∵AO是∠BAC的平分线,OM⊥AB,OE⊥AC,OE=2,
∴OM=OE=2,
∵CO是∠ACD的平分线,OE⊥AC,ON⊥CD,
∴ON=OE=2,
∴MN=OM+ON=4,
即AB与CD之间的距离是4.
故选:B.
14.解:A、AB=DC,不能根据SAS证两三角形全等,故本选项错误;
B、∵在△AOB和△DOC中
,
∴△AOB≌△DOC(SAS),故本选项正确;
C、两三角形相等的条件只有OA=OD和∠AOB=∠DOC,不能证两三角形全等,故本选项错误;
D、根据∠AOB=∠DOC和OA=OD,不能证两三角形全等,故本选项错误;
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
15.解:∵42=16,
∴=4.
故答案为:4.
16.解:∵一个正数的平方根是a+3和2a﹣15,
∴a+3和2a﹣15互为相反数,
即(a+3)+(2a﹣15)=0;
解得a=4,
则a+3=﹣(2a﹣15)=7;
则这个数为72=49;
故答案为49.
17.解:①开方开不尽的数是无理数,但是有的数不开方也是无理数,如:π,等,因此①不正确,不符合题意;
②满足﹣<x<的x的整数有﹣1,0,1,2共4个,因此②正确,符合题意;
③﹣3是9的一个平方根,而=9,因此③正确,符合题意;
④π就是无理数,不带根号的数也不一定是有理数,因此④不正确,不符合题意;
⑤无限循环小数,即分数是有理数,因此⑤不正确,不符合题意;
⑥若a<0,则=|a|=﹣a,因此⑥不正确,不符合题意;
因此正确的结论有②③,
故答案为:②③.
18.解:原式=2+3=;
故答案为:5.
19.解:∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC AD=×4×AD=12,
解得AD=6(cm),
∵EF是线段AB的垂直平分线,
∴AM=BM,
∴BM+MD=AM+DM=AD=6(cm),
故答案为:6.
20.解:∵△BCD为等边三角形,
∴∠DBC=60°,DB=BC=CD,
∵∠ABC=90°,
∴∠ABD=30°,
∵在Rt△ABC中,∠ABD=30°,AD=2
∴DB=4,
∴CD=BC=4,
在Rt△ABC中,由勾股定理,得AB===2,
∴四边形ABCD的周长=AB+BC+CD+DA=2+4+4+2=2+10,
故答案为:2+10.
三.解答题(共6小题,满分60分,每小题10分)
21.解:(1)原式=3﹣5+
=﹣;
(2)原式=3﹣5+3﹣﹣2
=﹣2.
22.解:(1)如图,点O为所作;
(2)过O点作OH⊥BC于H,如图,
∵∠A=40°,∠ABC=80°,
∴∠ACB=180°﹣∠A﹣∠ABC=180°﹣40°﹣80°=60°,
∵点O到AC、BC两边的距离相等,
∴CO平分∠ACB,
∴∠OCH=30°,
∴OB=OC=×6=3,
即点O到BC的距离为3.
23.解:原式=+
=+
=
=
=.
24.解:Rt△ABC中,∠B=90°,
设BC=a(m),AC=b(m),AD=x(m)
则10+a=x+b=15(m).
∴a=5(m),b=15﹣x(m)
又在Rt△ABC中,由勾股定理得:(10+x)2+a2=b2,
∴(10+x)2+52=(15﹣x)2,
解得,x=2,即AD=2(米)
∴AB=AD+DB=2+10=12(米)
答:树高AB为12米.
25.解:(1)∵OM是线段AB的垂直平分线,
∴DA=DB,
同理,EA=EC,
∵△ADE的周长13,
∴AD+DE+EA=13,
∴BC=DB+DE+EC=AD+DE+EA=13(cm);
(2)连接OB,OC,
∵△OBC的周长为27,
∴OB+OC+BC=27,
∵BC=13,
∴OB+OC=14,
∵OM垂直平分AB,
∴OA=OB,
同理,OA=OC,
∴OA=OB=OC=7(cm),
故答案为:7.
26.证明:∵D是BC的中点,
∴BD=CD,
∵DF∥AB,
∴∠B=∠CDF,
∵DE∥AC,
∴∠C=∠BDE,
在△BDE和△DCF中,,
∴△BDE≌△DCF(ASA),
∴BE=DF,DE=CF.
同课章节目录
