江苏省连云港市灌南县扬州路实验学校2021-2022学年七年级数学上册 周周练第13周试卷B卷(图片含答案)
文档属性
| 名称 | 江苏省连云港市灌南县扬州路实验学校2021-2022学年七年级数学上册 周周练第13周试卷B卷(图片含答案) |  | |
| 格式 | |||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 08:13:54 | ||
图片预览
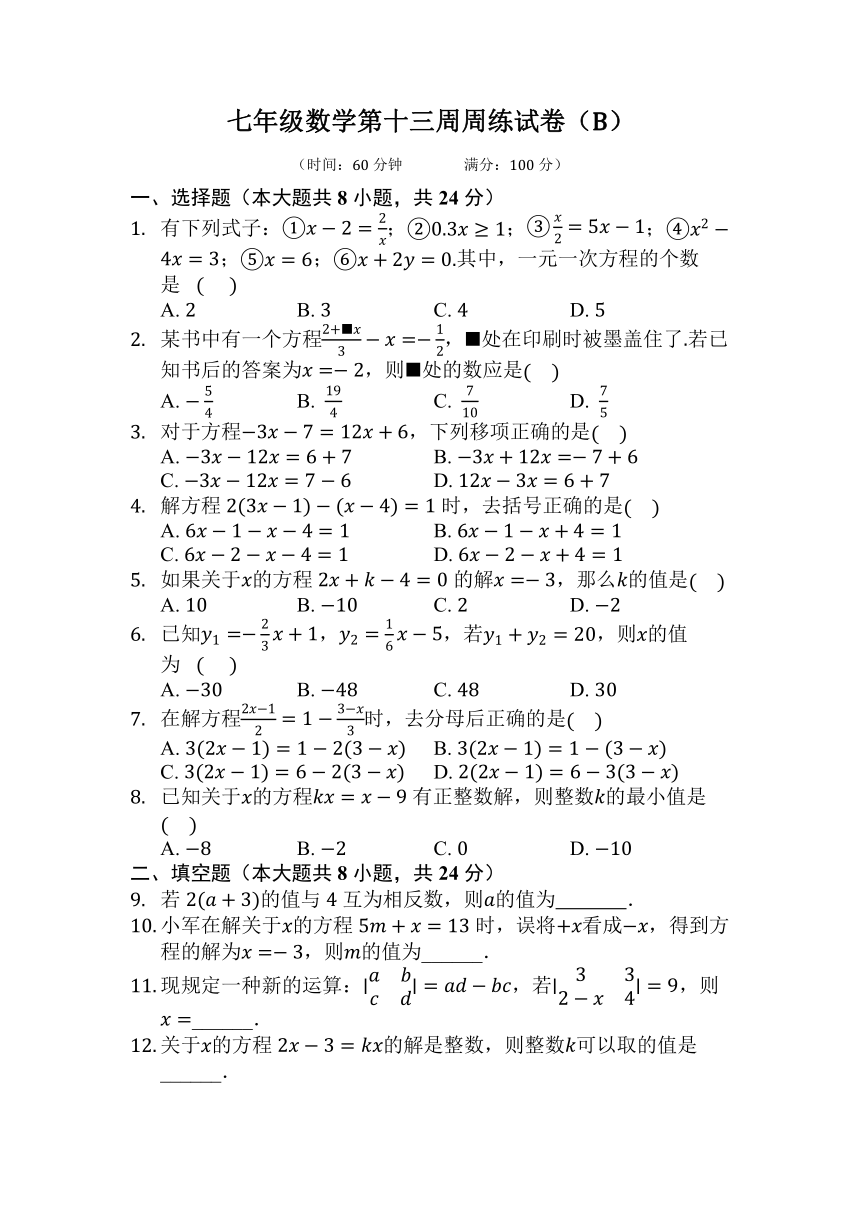




文档简介
七年级数学第十三周周练试卷(B)
(时间:60分钟 满分:100分)
一、选择题(本大题共 8 小题,共 24 分)
1. 2有下列式子:① 2 = ;②0.3 ≥ 1;③ = 5 1; 2 ④
2
4 = 3;⑤ = 6;⑥ +2 = 0.其中,一元一次方程的个数
是 ( )
A. 2 B. 3 C. 4 D. 5
2. 2+■ 1某书中有一个方程 = ,■处在印刷时被墨盖住了.若已
3 2
知书后的答案为 = 2,则■处的数应是( )
A. 5 B. 19 C. 7 D. 7
4 4 10 5
3. 对于方程 3 7 = 12 + 6,下列移项正确的是( )
A. 3 12 = 6 + 7 B. 3 + 12 = 7 + 6
C. 3 12 = 7 6 D. 12 3 = 6 + 7
4. 解方程 2(3 1) ( 4) = 1时,去括号正确的是( )
A. 6 1 4 = 1 B. 6 1 + 4 = 1
C. 6 2 4 = 1 D. 6 2 + 4 = 1
5. 如果关于 的方程 2 + 4 = 0的解 = 3,那么 的值是( )
A. 10 B. 10 C. 2 D. 2
6. 已知 1 =
2 + 1 1, 2 = 5,若 1 + 2 = 20,则 的值3 6
为 ( )
A. 30 B. 48 C. 48 D. 30
7. 2 1 = 1 3 在解方程 时,去分母后正确的是
2 3 ( )
A. 3(2 1) = 1 2(3 ) B. 3(2 1) = 1 (3 )
C. 3(2 1) = 6 2(3 ) D. 2(2 1) = 6 3(3 )
8. 已知关于 的方程 = 9有正整数解,则整数 的最小值是
( )
A. 8 B. 2 C. 0 D. 10
二、填空题(本大题共 8 小题,共 24 分)
9. 若 2( + 3)的值与 4互为相反数,则 的值为 .
10.小军在解关于 的方程 5 + = 13时,误将+ 看成 ,得到方
程的解为 = 3,则 的值为______.
11. 3 3现规定一种新的运算: = ,若 2 4 = 9,则
=______.
12.关于 的方程 2 3 = 的解是整数,则整数 可以取的值是
______.
13.方程 3 +▲ = 2,▲处被墨水盖住了,已知方程的解是 = 2,
那么▲处的数字是_____.
14.若 3 + 2 = 12和方程 3 4 = 2的解相同,则 =__________.
15.当 = 时,代数式 7 5( 2)的值是 8.
16.已知关于 的一元一次方程 + 5 = 2019 + 2019 的解为 = 2018,
5
那么关于 的一元一次方程 5 = 2019(5 ) 的解为
2019
______.
三、解答题(本大题共 5 小题,共 52 分)
17.(20分)解方程:
(1)3( + 2) = 2 (2)5( 1) 2(1 ) = 3 + 2
(3) (4) .
18.(6分)已知 1 = + 3, 2 = 2 ,当 取何值时, 1比 2 2
大 5.
第 2页,共 11页
19. 1 3 1 (8分)马虎同学在解方程 = 时,不小心把等式左边
2 3
前面的“ ”当做“+”进行求解,得到的结果为 = 1,求代
数式 2 2 + 1的值.
20.(8分)已知(| | 1) 2 ( + 1) + 8 = 0是关于 的一元一次
方程.
(1)求 的值,并解出上述一元一次方程;
(2)若上述方程的解比方程 5 2 = 2 的解大 2,求 的值.
21. 1(10分)我们知道 可以写成小数形式为 0.3,反过来,无限循
3
环小数 0.3也可以转化成分数形式.
方法如下:设 = 0.3,由 0.3 = 0.333…可知:10 = 3.333…,
所以 10 = 3.
解方程,得 = 1,所以 0.
3 3 =
1
.
3
再例如把无限循环小数 0.32化为分数方法:
设 = 0.32,由 0.32 = 0.323232…可知:100 = 32.323232…,
所以 100 = 32 32 32,解方程,得 = ,所以 0. .
99 32 = 99
【问题回答】
(1)把下列无限循环小数写成分数形式;
①0.5 =______;②2.58______;③0.518 =______.
(2)借鉴材料中的方法,从第(1)题的②,③中任选一个,验证你
的结果.
参考答案
1.【答案】
【解析】略
2.【答案】
【解析】
【分析】
本题考查了解一元一次方程,■用 代替,则把 = 2代入方程即可得到一个关于 的方程,
从而求得 的值.
【解答】
2 2 1
解:■用 代替,则把 = 2代入方程得: + 2 = ,
3 2
= 19解得: .
4
故选 B.
3.【答案】
【解析】解:移项得: 3 12 = 6 + 7,
故选: .
利用等式的基本性质 1,移项要变号变形得到结果,即可作出判断.
此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.
4.【答案】
【解析】解:去括号得:6 2 + 4 = 1,
故选: .
方程去括号得到结果,即可作出判断.
此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为 1,
第 4页,共 11页
求出解.
5.【答案】
【解析】
【分析】
本题考查一元一次方程的解的问题。已知条件中涉及到方程的解,把方程的解代入原方程,
转化为关于字母 的方程进行求解即可。
【解答】把 = 3代入方程 2 + 4 = 0,
得: 6 + 4 = 0
解得: = 10.
故选: .
6.【答案】
【解析】略
7.【答案】
2 1 3
【解析】解:方程 = 1 去分母,
2 3
方程两边都乘以 6得:3(2 1) = 6 2(3 ),
故选: 。
方程左右两边乘以 6去分母得到结果,即可作出判断。
此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键。
8.【答案】
【解析】
【分析】
本题考查了一元一次方程的解和解一元一次方程,能得出关于 的方程是解此题的关键.先
求出方程的解,根据已知得出 1 = 9或 3或 1,求出即可.
【解答】
解:解方程 = 9,
= 9,
( 1) = 9,
= 9,
1
∵关于 的方程 = 9有正整数解, 为整数,
∴ 1 = 9或 3或 1,
解得: = 8或 2或 0,
的最小值是 8,
故选 A.
9.【答案】 5
【解析】
【分析】
本题主要考查的是相反数的定义有关知识,依据相反数的定义列出关于 的方程求解即可.
【解答】
解:∵ 2( + 3)的值与 4互为相反数,
∴ 2( + 3) = 4,
解得: = 5.
故答案为 5.
10.【答案】2
【解析】解:根据题意得:5 = 13,
把 = 3代入得:5 + 3 = 13,
移项合并得:5 = 10,
解得: = 2,
故答案为:2
将错就错,把 = 3代入错误方程计算即可求出 的值.
此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
11.【答案】1
【解析】解:根据题中的新定义化简得:12 3(2 ) = 9,
去括号得:12 6 + 3 = 9,
移项合并得:3 = 3,
解得: = 1,
故答案为:1
已知等式利用题中的新定义化简,求出解即可得到 的值.
第 6页,共 11页
此题考查了解一元一次方程,以及有理数的混合运算,熟练掌握运算法则是解本题的关键.
12.【答案】±1或 3或 5
【解析】解:移项、合并,得(2 ) = 3,
解得 = 3 ,
2
∵ 为整数, 为整数,
∴ 3 =± 1 3, =± 3,
2 2
解得 =± 1或 3或 5.
故答案为:±1或 3或 5.
把含 的项合并,化系数为 1求 ,再根据 为正整数求整数 的值.
本题考查了一元一次方程的解.关键是按照字母系数解方程,再根据正整数解的要求求整数
的值.
13.【答案】 4
【解析】
【分析】
此题考查的是一元一次方程的解的定义,就是能够使方程左右两边相等的未知数的值.
把 = 2 代入已知方程,可以列出关于▲的方程,通过解该方程可以求得▲的值.
【解答】
解:由题意,得 6 +▲ = 2,
解得▲ = 4.
14.【答案】3
【解析】
【分析】
本题考查了方程的解,一元一次方程的解法,此题考查了同解方程,同解方程即为解相等的
方程.求出第二个方程的解得到 的值,代入第一个方程即可求出 的值.
【解答】
解:3 4 = 2,
移项合并得:3 = 6,
解得: = 2,
将 = 2 代入 3 + 2 = 12中得:
6 + 2 = 12,
解得: = 3.
故答案为 3.
15.【答案】5
【解析】略
16.【答案】2023
【解析】解:根据题意得:
方程 + 5 = 2019 +
2019 可整理得:
2019 = 5
2019 ,
则该方程的解为 = 2018,
5
方程 5 = 2019(5 ) 5 可整理得: 2019(5 ) = 5 ,
2019 2019
令 = 5 ,
则原方程可整理得: 2019 = 5 2019 ,
则 = 2018,
即 5 = 2018,
解得: = 2023,
故答案为:2023.
方程 + 5 = 2019 + 2019 可整理得: 2019 = 52019 ,则该方程的解为 = 2018,方
5
程 5 = 2019(5 ) 5 可整理得: 2019(5 ) = 5 ,令 = 5 ,则原
2019 2019
方程可整理得: 2019 = 5 2019 ,则 = 2018,得到关于 的一元一次方程,解之即
可.
本题考查了一元一次方程的解,正确掌握转化思想是解题的关键.
第 8页,共 11页
17.【答案】解:(1)去括号,得 3 + 6 = 2 ,
移项,得 3 + = 2 6,
合并同类项,得 4 = 4,
系数化成 1,得 = 1;
(2)去括号,得 5 5 2 + 2 = 3 + 2 ,
移项,得 5 + 2 2 = 3 + 5 + 2,
合并同类项,得 5 = 10,
系数化成 1,得 = 2;
(3)去分母得:6 + 9 = 6 + 1,
移项得:6 6 + = 1 9,
解得: = 8.
(4) 10 6 +10方程变形得: + = ,
4 3
去分母得:30 18 + 12 = 4 + 40,
移项合并得:38 = 58,
29
解得: = .
19
【解析】本题主要考查一元一次方程的解法.
(1)先去括号,然后移项,合并同类项,最后把系数化成 1;
(2)先去括号,然后移项,合并同类项,最后把系数化成 1;
(3)先去分母,然后去括号,移项,合并同类项,最后把系数化成 1;
(4)先去分母,然后去括号,移项,合并同类项,最后把系数化成 1.
18.【答案】解:∵ 1 = + 3, 2 = 2 , 1比 2 2大 5.,
∴ + 3 2(2 ) = 5,
∴ = 2,即 = 2 时, 1比 2 2大 5.
【解析】由于 1比 2 2大 5,由此可以得到 + 3 2(2 ) = 5,而后解此方程即可求出
的值.
考查了解一元一次方程,首先利用已知条件得到关于 的方程,然后解方程即可解决问题.
19. = 1 1 3 + = 1 1+ = 1 【答案】解:把 代入方程 得: ,2 3 3
解得: = 1,
当 = 1时, 2 2 + 1 = 1 2+ 1 = 0.
【解析】把 = 1 1 3 1 代入方程 + = 得出方程,求出 ,最后再代入求出即可.
2 3
本题考查了一元一次方程的解和解一元一次方程,能得出关于 的方程是解此题的关键.
20.【答案】解:(1)因为(| | 1) 2 ( + 1) + 8 = 0 是关于 的一元一次方程,
所以| | 1 = 0 且 ( + 1) ≠ 0.
由| | 1 = 0,得| | = 1,所以 =± 1.
由 ( + 1) ≠ 0,得 + 1 ≠ 0,所以 ≠ 1,
所以 = 1.
所以方程可转化为 2 + 8 = 0.
移项,得 2 = 8.
系数化为 1,得 = 4.
(2)因为方程 2 + 8 = 0 的解比方程 5 2 = 2 的解大 2,
所以方程 5 2 = 2 的解为 = 2.
所以 5 × 2 2 = 2 × 2.
移项,得 2 = 4 10.
合并同类项,得 2 = 6.
系数化为 1,得 = 3.
第 10页,共 11页
【解析】此题考查了一元一次方程的定义和解一元一次方程,熟练掌握运算法则是解本题的
关键.
(1)利用一元一次方程的定义求出 的值,求出一元一次方程的解即可;
(2)由上述方程的解确定出 5 2 = 2 的解,代入计算即可求出 的值.
21.【答案】(1)① 5 ② 256 ③ 518, , ;9 99 999
(2)①设 = 0.5,则 10 = 5.5555…,所以 10 = 5,
= 5
5
解方程,得 ,所以 0. ;
9 5 = 9
②设 = 0.58,则 100 = 58.5858,所以 100 = 58.
= 58 2 58 = 2 + 58解方程,得 ,所以 .99 =
256
.
99 99
③设 = 0.518,则 1000 = 518.518518…,所以 1000 = 518.
518 518
解方程,得 = ,所以 0.518 = .999 999
5 256
【解析】解:(1)0.5 = ;2.58 = . 0.518 = 518.
9 99 999
5 256 518
故答案为:① ;② ;③ ;
9 99 999
(2)见答案.
仿照题中无限循环小数写为分数形式的方法,设未知数,根据小数点的们位数扩大 10倍或
100倍或 1000倍计算即可.
此题考查了解一元一次方程,弄清题中无限循环小数化为分数的方法是解本题的关键.
(时间:60分钟 满分:100分)
一、选择题(本大题共 8 小题,共 24 分)
1. 2有下列式子:① 2 = ;②0.3 ≥ 1;③ = 5 1; 2 ④
2
4 = 3;⑤ = 6;⑥ +2 = 0.其中,一元一次方程的个数
是 ( )
A. 2 B. 3 C. 4 D. 5
2. 2+■ 1某书中有一个方程 = ,■处在印刷时被墨盖住了.若已
3 2
知书后的答案为 = 2,则■处的数应是( )
A. 5 B. 19 C. 7 D. 7
4 4 10 5
3. 对于方程 3 7 = 12 + 6,下列移项正确的是( )
A. 3 12 = 6 + 7 B. 3 + 12 = 7 + 6
C. 3 12 = 7 6 D. 12 3 = 6 + 7
4. 解方程 2(3 1) ( 4) = 1时,去括号正确的是( )
A. 6 1 4 = 1 B. 6 1 + 4 = 1
C. 6 2 4 = 1 D. 6 2 + 4 = 1
5. 如果关于 的方程 2 + 4 = 0的解 = 3,那么 的值是( )
A. 10 B. 10 C. 2 D. 2
6. 已知 1 =
2 + 1 1, 2 = 5,若 1 + 2 = 20,则 的值3 6
为 ( )
A. 30 B. 48 C. 48 D. 30
7. 2 1 = 1 3 在解方程 时,去分母后正确的是
2 3 ( )
A. 3(2 1) = 1 2(3 ) B. 3(2 1) = 1 (3 )
C. 3(2 1) = 6 2(3 ) D. 2(2 1) = 6 3(3 )
8. 已知关于 的方程 = 9有正整数解,则整数 的最小值是
( )
A. 8 B. 2 C. 0 D. 10
二、填空题(本大题共 8 小题,共 24 分)
9. 若 2( + 3)的值与 4互为相反数,则 的值为 .
10.小军在解关于 的方程 5 + = 13时,误将+ 看成 ,得到方
程的解为 = 3,则 的值为______.
11. 3 3现规定一种新的运算: = ,若 2 4 = 9,则
=______.
12.关于 的方程 2 3 = 的解是整数,则整数 可以取的值是
______.
13.方程 3 +▲ = 2,▲处被墨水盖住了,已知方程的解是 = 2,
那么▲处的数字是_____.
14.若 3 + 2 = 12和方程 3 4 = 2的解相同,则 =__________.
15.当 = 时,代数式 7 5( 2)的值是 8.
16.已知关于 的一元一次方程 + 5 = 2019 + 2019 的解为 = 2018,
5
那么关于 的一元一次方程 5 = 2019(5 ) 的解为
2019
______.
三、解答题(本大题共 5 小题,共 52 分)
17.(20分)解方程:
(1)3( + 2) = 2 (2)5( 1) 2(1 ) = 3 + 2
(3) (4) .
18.(6分)已知 1 = + 3, 2 = 2 ,当 取何值时, 1比 2 2
大 5.
第 2页,共 11页
19. 1 3 1 (8分)马虎同学在解方程 = 时,不小心把等式左边
2 3
前面的“ ”当做“+”进行求解,得到的结果为 = 1,求代
数式 2 2 + 1的值.
20.(8分)已知(| | 1) 2 ( + 1) + 8 = 0是关于 的一元一次
方程.
(1)求 的值,并解出上述一元一次方程;
(2)若上述方程的解比方程 5 2 = 2 的解大 2,求 的值.
21. 1(10分)我们知道 可以写成小数形式为 0.3,反过来,无限循
3
环小数 0.3也可以转化成分数形式.
方法如下:设 = 0.3,由 0.3 = 0.333…可知:10 = 3.333…,
所以 10 = 3.
解方程,得 = 1,所以 0.
3 3 =
1
.
3
再例如把无限循环小数 0.32化为分数方法:
设 = 0.32,由 0.32 = 0.323232…可知:100 = 32.323232…,
所以 100 = 32 32 32,解方程,得 = ,所以 0. .
99 32 = 99
【问题回答】
(1)把下列无限循环小数写成分数形式;
①0.5 =______;②2.58______;③0.518 =______.
(2)借鉴材料中的方法,从第(1)题的②,③中任选一个,验证你
的结果.
参考答案
1.【答案】
【解析】略
2.【答案】
【解析】
【分析】
本题考查了解一元一次方程,■用 代替,则把 = 2代入方程即可得到一个关于 的方程,
从而求得 的值.
【解答】
2 2 1
解:■用 代替,则把 = 2代入方程得: + 2 = ,
3 2
= 19解得: .
4
故选 B.
3.【答案】
【解析】解:移项得: 3 12 = 6 + 7,
故选: .
利用等式的基本性质 1,移项要变号变形得到结果,即可作出判断.
此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.
4.【答案】
【解析】解:去括号得:6 2 + 4 = 1,
故选: .
方程去括号得到结果,即可作出判断.
此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为 1,
第 4页,共 11页
求出解.
5.【答案】
【解析】
【分析】
本题考查一元一次方程的解的问题。已知条件中涉及到方程的解,把方程的解代入原方程,
转化为关于字母 的方程进行求解即可。
【解答】把 = 3代入方程 2 + 4 = 0,
得: 6 + 4 = 0
解得: = 10.
故选: .
6.【答案】
【解析】略
7.【答案】
2 1 3
【解析】解:方程 = 1 去分母,
2 3
方程两边都乘以 6得:3(2 1) = 6 2(3 ),
故选: 。
方程左右两边乘以 6去分母得到结果,即可作出判断。
此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键。
8.【答案】
【解析】
【分析】
本题考查了一元一次方程的解和解一元一次方程,能得出关于 的方程是解此题的关键.先
求出方程的解,根据已知得出 1 = 9或 3或 1,求出即可.
【解答】
解:解方程 = 9,
= 9,
( 1) = 9,
= 9,
1
∵关于 的方程 = 9有正整数解, 为整数,
∴ 1 = 9或 3或 1,
解得: = 8或 2或 0,
的最小值是 8,
故选 A.
9.【答案】 5
【解析】
【分析】
本题主要考查的是相反数的定义有关知识,依据相反数的定义列出关于 的方程求解即可.
【解答】
解:∵ 2( + 3)的值与 4互为相反数,
∴ 2( + 3) = 4,
解得: = 5.
故答案为 5.
10.【答案】2
【解析】解:根据题意得:5 = 13,
把 = 3代入得:5 + 3 = 13,
移项合并得:5 = 10,
解得: = 2,
故答案为:2
将错就错,把 = 3代入错误方程计算即可求出 的值.
此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
11.【答案】1
【解析】解:根据题中的新定义化简得:12 3(2 ) = 9,
去括号得:12 6 + 3 = 9,
移项合并得:3 = 3,
解得: = 1,
故答案为:1
已知等式利用题中的新定义化简,求出解即可得到 的值.
第 6页,共 11页
此题考查了解一元一次方程,以及有理数的混合运算,熟练掌握运算法则是解本题的关键.
12.【答案】±1或 3或 5
【解析】解:移项、合并,得(2 ) = 3,
解得 = 3 ,
2
∵ 为整数, 为整数,
∴ 3 =± 1 3, =± 3,
2 2
解得 =± 1或 3或 5.
故答案为:±1或 3或 5.
把含 的项合并,化系数为 1求 ,再根据 为正整数求整数 的值.
本题考查了一元一次方程的解.关键是按照字母系数解方程,再根据正整数解的要求求整数
的值.
13.【答案】 4
【解析】
【分析】
此题考查的是一元一次方程的解的定义,就是能够使方程左右两边相等的未知数的值.
把 = 2 代入已知方程,可以列出关于▲的方程,通过解该方程可以求得▲的值.
【解答】
解:由题意,得 6 +▲ = 2,
解得▲ = 4.
14.【答案】3
【解析】
【分析】
本题考查了方程的解,一元一次方程的解法,此题考查了同解方程,同解方程即为解相等的
方程.求出第二个方程的解得到 的值,代入第一个方程即可求出 的值.
【解答】
解:3 4 = 2,
移项合并得:3 = 6,
解得: = 2,
将 = 2 代入 3 + 2 = 12中得:
6 + 2 = 12,
解得: = 3.
故答案为 3.
15.【答案】5
【解析】略
16.【答案】2023
【解析】解:根据题意得:
方程 + 5 = 2019 +
2019 可整理得:
2019 = 5
2019 ,
则该方程的解为 = 2018,
5
方程 5 = 2019(5 ) 5 可整理得: 2019(5 ) = 5 ,
2019 2019
令 = 5 ,
则原方程可整理得: 2019 = 5 2019 ,
则 = 2018,
即 5 = 2018,
解得: = 2023,
故答案为:2023.
方程 + 5 = 2019 + 2019 可整理得: 2019 = 52019 ,则该方程的解为 = 2018,方
5
程 5 = 2019(5 ) 5 可整理得: 2019(5 ) = 5 ,令 = 5 ,则原
2019 2019
方程可整理得: 2019 = 5 2019 ,则 = 2018,得到关于 的一元一次方程,解之即
可.
本题考查了一元一次方程的解,正确掌握转化思想是解题的关键.
第 8页,共 11页
17.【答案】解:(1)去括号,得 3 + 6 = 2 ,
移项,得 3 + = 2 6,
合并同类项,得 4 = 4,
系数化成 1,得 = 1;
(2)去括号,得 5 5 2 + 2 = 3 + 2 ,
移项,得 5 + 2 2 = 3 + 5 + 2,
合并同类项,得 5 = 10,
系数化成 1,得 = 2;
(3)去分母得:6 + 9 = 6 + 1,
移项得:6 6 + = 1 9,
解得: = 8.
(4) 10 6 +10方程变形得: + = ,
4 3
去分母得:30 18 + 12 = 4 + 40,
移项合并得:38 = 58,
29
解得: = .
19
【解析】本题主要考查一元一次方程的解法.
(1)先去括号,然后移项,合并同类项,最后把系数化成 1;
(2)先去括号,然后移项,合并同类项,最后把系数化成 1;
(3)先去分母,然后去括号,移项,合并同类项,最后把系数化成 1;
(4)先去分母,然后去括号,移项,合并同类项,最后把系数化成 1.
18.【答案】解:∵ 1 = + 3, 2 = 2 , 1比 2 2大 5.,
∴ + 3 2(2 ) = 5,
∴ = 2,即 = 2 时, 1比 2 2大 5.
【解析】由于 1比 2 2大 5,由此可以得到 + 3 2(2 ) = 5,而后解此方程即可求出
的值.
考查了解一元一次方程,首先利用已知条件得到关于 的方程,然后解方程即可解决问题.
19. = 1 1 3 + = 1 1+ = 1 【答案】解:把 代入方程 得: ,2 3 3
解得: = 1,
当 = 1时, 2 2 + 1 = 1 2+ 1 = 0.
【解析】把 = 1 1 3 1 代入方程 + = 得出方程,求出 ,最后再代入求出即可.
2 3
本题考查了一元一次方程的解和解一元一次方程,能得出关于 的方程是解此题的关键.
20.【答案】解:(1)因为(| | 1) 2 ( + 1) + 8 = 0 是关于 的一元一次方程,
所以| | 1 = 0 且 ( + 1) ≠ 0.
由| | 1 = 0,得| | = 1,所以 =± 1.
由 ( + 1) ≠ 0,得 + 1 ≠ 0,所以 ≠ 1,
所以 = 1.
所以方程可转化为 2 + 8 = 0.
移项,得 2 = 8.
系数化为 1,得 = 4.
(2)因为方程 2 + 8 = 0 的解比方程 5 2 = 2 的解大 2,
所以方程 5 2 = 2 的解为 = 2.
所以 5 × 2 2 = 2 × 2.
移项,得 2 = 4 10.
合并同类项,得 2 = 6.
系数化为 1,得 = 3.
第 10页,共 11页
【解析】此题考查了一元一次方程的定义和解一元一次方程,熟练掌握运算法则是解本题的
关键.
(1)利用一元一次方程的定义求出 的值,求出一元一次方程的解即可;
(2)由上述方程的解确定出 5 2 = 2 的解,代入计算即可求出 的值.
21.【答案】(1)① 5 ② 256 ③ 518, , ;9 99 999
(2)①设 = 0.5,则 10 = 5.5555…,所以 10 = 5,
= 5
5
解方程,得 ,所以 0. ;
9 5 = 9
②设 = 0.58,则 100 = 58.5858,所以 100 = 58.
= 58 2 58 = 2 + 58解方程,得 ,所以 .99 =
256
.
99 99
③设 = 0.518,则 1000 = 518.518518…,所以 1000 = 518.
518 518
解方程,得 = ,所以 0.518 = .999 999
5 256
【解析】解:(1)0.5 = ;2.58 = . 0.518 = 518.
9 99 999
5 256 518
故答案为:① ;② ;③ ;
9 99 999
(2)见答案.
仿照题中无限循环小数写为分数形式的方法,设未知数,根据小数点的们位数扩大 10倍或
100倍或 1000倍计算即可.
此题考查了解一元一次方程,弄清题中无限循环小数化为分数的方法是解本题的关键.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
