3.4正、反比例整理与复习(课件) 数学六年级下册(共21张PPT)
文档属性
| 名称 | 3.4正、反比例整理与复习(课件) 数学六年级下册(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 14:55:34 | ||
图片预览







文档简介
(共21张PPT)
六年级下册
3.4正、反比例的整理与复习
学习目标
1、结合具体情境,经历讨论和总结正、反比例关系式及字母表达式的过程。
2、在常见数量关系的三种量中,知道某种量是一定,另外两种量成什么关系;理解正、反比例的字母表达式和含义。
3、在讨论和判断正、反比例量的过程中,能进行有条理的思考,能清楚地表达和思考的过程和结果。
知识梳理
1、路程和时间是两种( )的量,路程随着时间的变化而变化,而且,路程和时间的( )一定(速度一定)。我们就说路程和时间这两种量成( )比例。它们的关系叫做正比例关系。
2、两种相关联的量,一种量变化,另一种量也( ),如果这两种量中相对应的两个数的( )一定,这两种量就叫做成( )的量。它们的关系叫做正比例关系。
相关联
比值
正
随着变化
比值
正比例
知识梳理
3、表示正比例关系的图象是从横轴和竖轴的交点画出的一条( ),两种量的所有对应点都在( )上。
4、两种相关联的量,一种量变化,另一种量也( ),如果这两种量中相对应的两个数的( )一定,这两种量就叫做成( )的量。它们的关系叫做反比例关系。
射线上
这条射线
随着变化
积
正比例
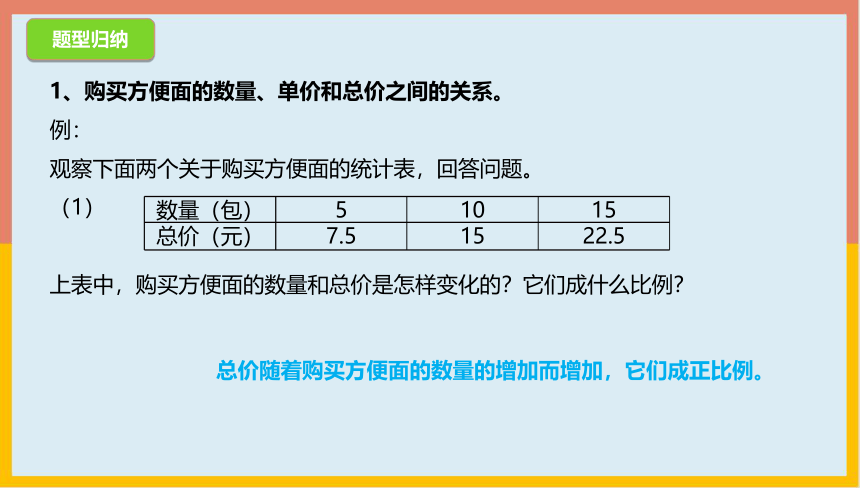
1、购买方便面的数量、单价和总价之间的关系。
例:
观察下面两个关于购买方便面的统计表,回答问题。
(1)
上表中,购买方便面的数量和总价是怎样变化的?它们成什么比例?
题型归纳
数量(包) 5 10 15
总价(元) 7.5 15 22.5
总价随着购买方便面的数量的增加而增加,它们成正比例。
1、购买方便面的数量、单价和总价之间的关系。
例:
观察下面两个关于购买方便面的统计表,回答问题。
(2)
上表中,购买方便面的单价和数量是怎样变化的?它们成什么比例?
题型归纳
数量随着方便面的单价的增加而减少,它们成反比例。
单价(元) 1.2 1.8 2.4
数量(包) 30 20 1.5
1、购买方便面的数量、单价和总价之间的关系。
例:
观察下面两个关于购买方便面的统计表,回答问题。
议一议:当总价一定时,单价和数量成反比例。
当数量一定时,总价和单价成正比例。
当单价一定时,总价和数量成正比例。
题型归纳
当总价一定时,单价和数量成反比例。
当数量一定时,总价和单价成正比例。
当单价一定时,总价和数量成正比例。
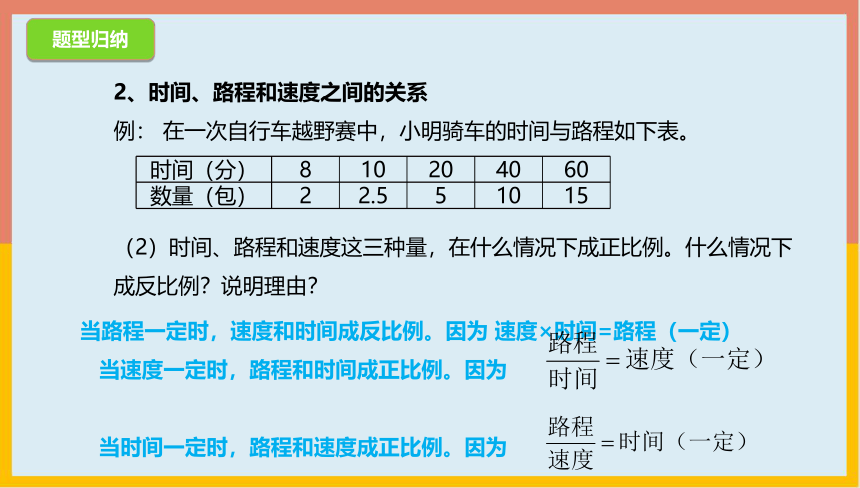
2、时间、路程和速度之间的关系
例: 在一次自行车越野赛中,小明骑车的时间与路程如下表。
(1)路程和时间成什么比例?
题型归纳
时间(分) 8 10 20 40 60
数量(包) 2 2.5 5 10 15
路程和时间成正比例。
2、时间、路程和速度之间的关系
例: 在一次自行车越野赛中,小明骑车的时间与路程如下表。
(2)时间、路程和速度这三种量,在什么情况下成正比例。什么情况下成反比例?说明理由?
题型归纳
当路程一定时,速度和时间成反比例。因为 速度×时间=路程(一定)
当速度一定时,路程和时间成正比例。因为
当时间一定时,路程和速度成正比例。因为
时间(分) 8 10 20 40 60
数量(包) 2 2.5 5 10 15
3、正比例、反比例字母表示方法。
如果用字母x和y表示两种相关联的量,用k表示一定的量,
成正比例、反比例的关系可以怎样表示。
题型归纳
成正比例、反比例的关系可以分别用下面的式子表示。
正比例 反比例x·y=k
本课小结
正、反比例整理与复习
01
02
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量。它们的关系叫做反比例关系。反比例:x·y=k
随堂检测
汽车每次运货的吨数、运货的次数和运货的总吨数这三种量,在什么情况下成正比例,什么情况下成反比例?
当汽车每次运货的吨数一定时,运货的次数和运货的总吨数成正比例。
当汽车每次运货的次数一定时,运货的吨数和运货的总吨数成正比例。
当汽车每次运货的次数一定时,运货的吨数和运货的次数成反比例。
随堂检测
一个榨油厂用4台同样的榨油机每天榨油36 吨。
(1)题中哪种量是相关联的量?哪种量是一定的?
(2)榨油机的台数和每天榨油的吨数成正比例吗?为什么?
(3)照这样计算,6台这样的榨油机每天榨油多少吨?
榨油机和每天榨油的数量是相关联的量,每台榨油机的榨油数量是一定的。
榨油机的台数和每天榨油的吨数成正比例,因为每天榨油的吨数和榨油机的台数比值相等。
36÷4×6
=9×6
=54(吨)
答:照这样计算,6台这样的榨油机每天榨油54吨。
随堂检测
一个榨油厂用4台同样的榨油机每天榨油36 吨。
(4)把榨油机台数和每天榨油的吨数在上面的方格纸上表示出来。
随堂检测
下图表示每小时行驶60千米的汽车1小时、2小时、3小时……所行驶的路程。看图估计一下:这辆汽车2.5小时行驶多少千米?4.5小时呢?
这辆汽车2.5小时行驶160千米,这辆汽车,4.5小时行驶270千米
随堂检测
看图填表并回答问题。
大齿轮的转数与小齿轮的转数成什么比例?为什么?
大齿轮的转数(转) 1 2 3 4
小齿轮的转数(转) 3
6 9 12
大齿轮的转数与小齿轮的转数成正比例。因为它们的比值相等。
随堂检测
自行车运动员每天要骑车训练10小时,行300千米。某位运动员连续训练20天,一共要行多少千米?
300×20=6000(千米)
答:一共要行6000千米。
随堂检测
为了了解出租车的营运利润,李强对一辆出租车的营运情况做了一周的跟踪调查,结果如下:
按这一周每天利润的平均数计算,一辆出租车一个月(30天)可以获得利润多少元?
(112+105+96+101+86+118+124)÷7×30
=742÷7×30
=106×30
=3180(元)
答:一辆出租车一个月(30天)可以获得利润3180元。
随堂检测
先算出左边各题的积,再填写右表。
320
3200
3200
32000
64000
3200
3200
32000
64000
作业布置
1、手工编织厂要做一批工艺品,每人编织的个数和所需要的人数关系如下。
(1)每人编织的个数与所需要的人数这两种量成什么比例关系?为什么?
(2)如果每人编织80个,需要多少人?
2、预习第27、28页的有关内容。
空白演示
单击输入您的封面副标题
谢 谢 聆 听
六年级下册
3.4正、反比例的整理与复习
学习目标
1、结合具体情境,经历讨论和总结正、反比例关系式及字母表达式的过程。
2、在常见数量关系的三种量中,知道某种量是一定,另外两种量成什么关系;理解正、反比例的字母表达式和含义。
3、在讨论和判断正、反比例量的过程中,能进行有条理的思考,能清楚地表达和思考的过程和结果。
知识梳理
1、路程和时间是两种( )的量,路程随着时间的变化而变化,而且,路程和时间的( )一定(速度一定)。我们就说路程和时间这两种量成( )比例。它们的关系叫做正比例关系。
2、两种相关联的量,一种量变化,另一种量也( ),如果这两种量中相对应的两个数的( )一定,这两种量就叫做成( )的量。它们的关系叫做正比例关系。
相关联
比值
正
随着变化
比值
正比例
知识梳理
3、表示正比例关系的图象是从横轴和竖轴的交点画出的一条( ),两种量的所有对应点都在( )上。
4、两种相关联的量,一种量变化,另一种量也( ),如果这两种量中相对应的两个数的( )一定,这两种量就叫做成( )的量。它们的关系叫做反比例关系。
射线上
这条射线
随着变化
积
正比例
1、购买方便面的数量、单价和总价之间的关系。
例:
观察下面两个关于购买方便面的统计表,回答问题。
(1)
上表中,购买方便面的数量和总价是怎样变化的?它们成什么比例?
题型归纳
数量(包) 5 10 15
总价(元) 7.5 15 22.5
总价随着购买方便面的数量的增加而增加,它们成正比例。
1、购买方便面的数量、单价和总价之间的关系。
例:
观察下面两个关于购买方便面的统计表,回答问题。
(2)
上表中,购买方便面的单价和数量是怎样变化的?它们成什么比例?
题型归纳
数量随着方便面的单价的增加而减少,它们成反比例。
单价(元) 1.2 1.8 2.4
数量(包) 30 20 1.5
1、购买方便面的数量、单价和总价之间的关系。
例:
观察下面两个关于购买方便面的统计表,回答问题。
议一议:当总价一定时,单价和数量成反比例。
当数量一定时,总价和单价成正比例。
当单价一定时,总价和数量成正比例。
题型归纳
当总价一定时,单价和数量成反比例。
当数量一定时,总价和单价成正比例。
当单价一定时,总价和数量成正比例。
2、时间、路程和速度之间的关系
例: 在一次自行车越野赛中,小明骑车的时间与路程如下表。
(1)路程和时间成什么比例?
题型归纳
时间(分) 8 10 20 40 60
数量(包) 2 2.5 5 10 15
路程和时间成正比例。
2、时间、路程和速度之间的关系
例: 在一次自行车越野赛中,小明骑车的时间与路程如下表。
(2)时间、路程和速度这三种量,在什么情况下成正比例。什么情况下成反比例?说明理由?
题型归纳
当路程一定时,速度和时间成反比例。因为 速度×时间=路程(一定)
当速度一定时,路程和时间成正比例。因为
当时间一定时,路程和速度成正比例。因为
时间(分) 8 10 20 40 60
数量(包) 2 2.5 5 10 15
3、正比例、反比例字母表示方法。
如果用字母x和y表示两种相关联的量,用k表示一定的量,
成正比例、反比例的关系可以怎样表示。
题型归纳
成正比例、反比例的关系可以分别用下面的式子表示。
正比例 反比例x·y=k
本课小结
正、反比例整理与复习
01
02
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量。它们的关系叫做反比例关系。反比例:x·y=k
随堂检测
汽车每次运货的吨数、运货的次数和运货的总吨数这三种量,在什么情况下成正比例,什么情况下成反比例?
当汽车每次运货的吨数一定时,运货的次数和运货的总吨数成正比例。
当汽车每次运货的次数一定时,运货的吨数和运货的总吨数成正比例。
当汽车每次运货的次数一定时,运货的吨数和运货的次数成反比例。
随堂检测
一个榨油厂用4台同样的榨油机每天榨油36 吨。
(1)题中哪种量是相关联的量?哪种量是一定的?
(2)榨油机的台数和每天榨油的吨数成正比例吗?为什么?
(3)照这样计算,6台这样的榨油机每天榨油多少吨?
榨油机和每天榨油的数量是相关联的量,每台榨油机的榨油数量是一定的。
榨油机的台数和每天榨油的吨数成正比例,因为每天榨油的吨数和榨油机的台数比值相等。
36÷4×6
=9×6
=54(吨)
答:照这样计算,6台这样的榨油机每天榨油54吨。
随堂检测
一个榨油厂用4台同样的榨油机每天榨油36 吨。
(4)把榨油机台数和每天榨油的吨数在上面的方格纸上表示出来。
随堂检测
下图表示每小时行驶60千米的汽车1小时、2小时、3小时……所行驶的路程。看图估计一下:这辆汽车2.5小时行驶多少千米?4.5小时呢?
这辆汽车2.5小时行驶160千米,这辆汽车,4.5小时行驶270千米
随堂检测
看图填表并回答问题。
大齿轮的转数与小齿轮的转数成什么比例?为什么?
大齿轮的转数(转) 1 2 3 4
小齿轮的转数(转) 3
6 9 12
大齿轮的转数与小齿轮的转数成正比例。因为它们的比值相等。
随堂检测
自行车运动员每天要骑车训练10小时,行300千米。某位运动员连续训练20天,一共要行多少千米?
300×20=6000(千米)
答:一共要行6000千米。
随堂检测
为了了解出租车的营运利润,李强对一辆出租车的营运情况做了一周的跟踪调查,结果如下:
按这一周每天利润的平均数计算,一辆出租车一个月(30天)可以获得利润多少元?
(112+105+96+101+86+118+124)÷7×30
=742÷7×30
=106×30
=3180(元)
答:一辆出租车一个月(30天)可以获得利润3180元。
随堂检测
先算出左边各题的积,再填写右表。
320
3200
3200
32000
64000
3200
3200
32000
64000
作业布置
1、手工编织厂要做一批工艺品,每人编织的个数和所需要的人数关系如下。
(1)每人编织的个数与所需要的人数这两种量成什么比例关系?为什么?
(2)如果每人编织80个,需要多少人?
2、预习第27、28页的有关内容。
空白演示
单击输入您的封面副标题
谢 谢 聆 听
