苏科版八年级上册第二章 轴对称图形2.5等腰三角形 的轴对称性 复习课件(共20张PPT)
文档属性
| 名称 | 苏科版八年级上册第二章 轴对称图形2.5等腰三角形 的轴对称性 复习课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 796.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 08:27:26 | ||
图片预览





文档简介
(共20张PPT)
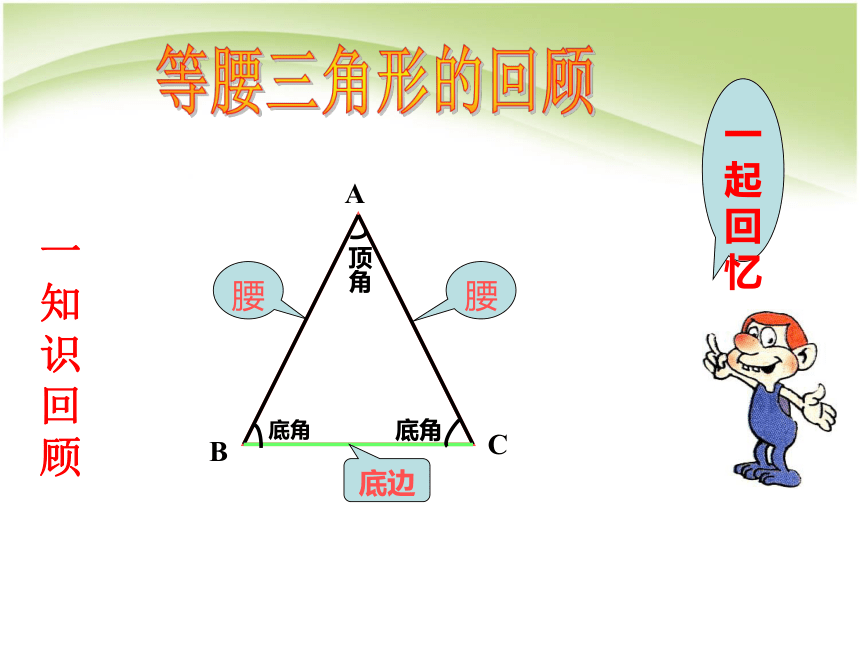
等腰三角形的轴对称性
A
C
B
腰
腰
底边
顶角
底角
底角
一起回忆
一知识回顾
三角形 性质
判定
等腰三角形
等边三角形
1.等边对等角。
2.三线合一 。
3.轴对称图形。
1.等角对等边。
2.定义:两边等的三角形是等腰三角形。
1.三边相等。
2.三个角都相等,每个角都是60°。
3.轴对称图形。
1.有一个角是60°
的等腰三角形是
等边三角形。
2.三个角相等的
三角形是等边三
角形。
热身练习
1.填空
1)、等腰三角形的一个顶角是100 ,则它的底角是______。
2)、等腰三角形的一个底角是50 ,则它的顶角是______。
3)、等腰三角形的一个内角等于70°,则它的底角等于____。
4)、等腰三角形底边是4cm,腰长是6cm,则它的周长是_____ cm
5)、等腰三角形有两边长分别为3cm、4cm,则周长为 _____ 。
6)、等腰三角形有两边长分别为2cm、4cm,则周长为 _____cm。
40
70 或55
80
10
16cm
10cm或11cm
思想方法:分类讨论
2.判断题
1)、等腰三角形的角平分线、中线和高互相重合。( )
2)、有一个角是60°的等腰三角形其它两内角也60°。( )
3)、三角形的三个外角都相等的三角形是等边三角形。( )
4)、等腰三角形的底角都是锐角。 ( )
5)、钝角三角形不可能是等腰三角形 。 ( )
×
√
√
√
×
难点突破
1 三角形ABC中,已知AB=AC,且∠B=80° ,则∠C= 度,∠A= 度?
80
20
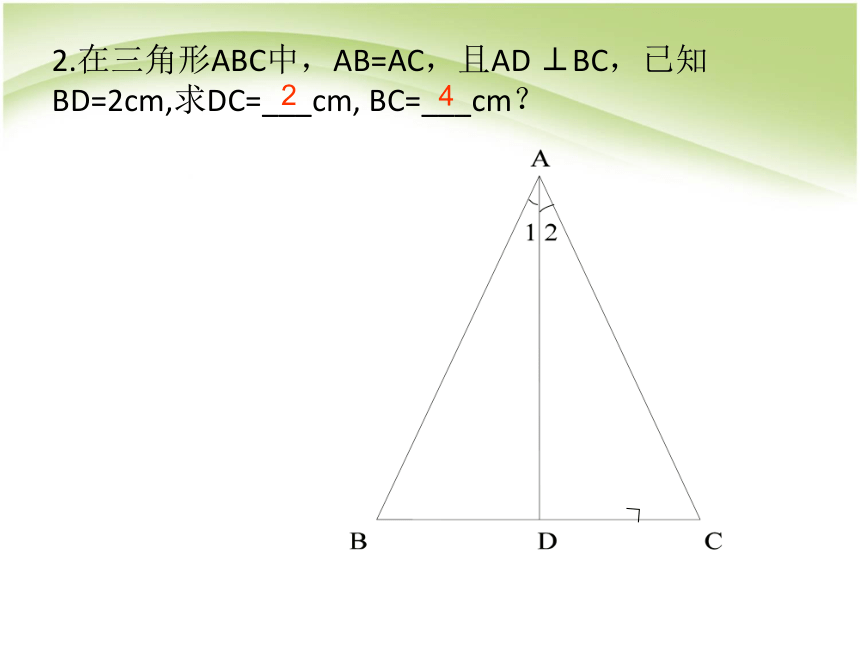
2.在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?
∟
2
4
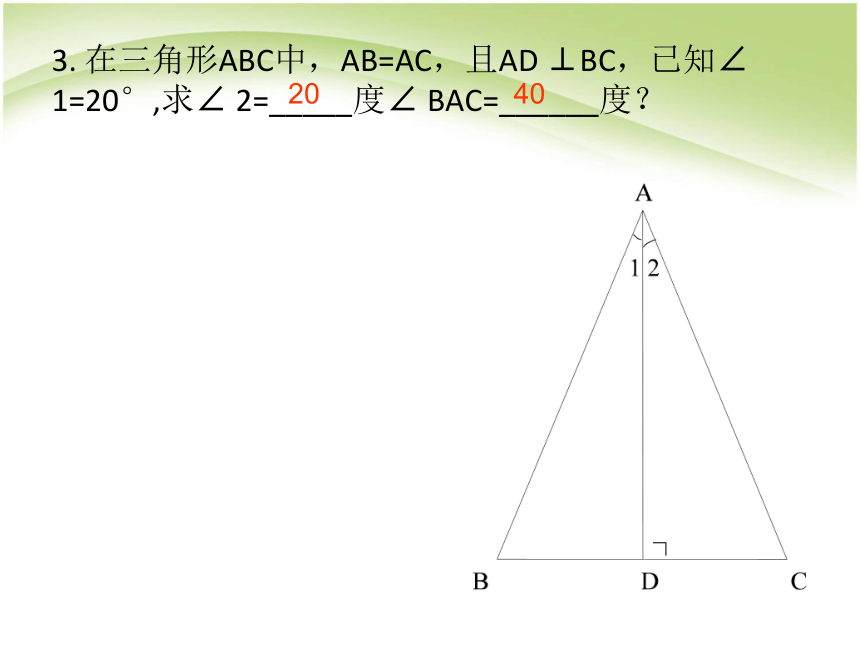
3. 在三角形ABC中,AB=AC,且AD ⊥BC,已知∠ 1=20°,求∠ 2=_____度∠ BAC=______度?
∟
20
40
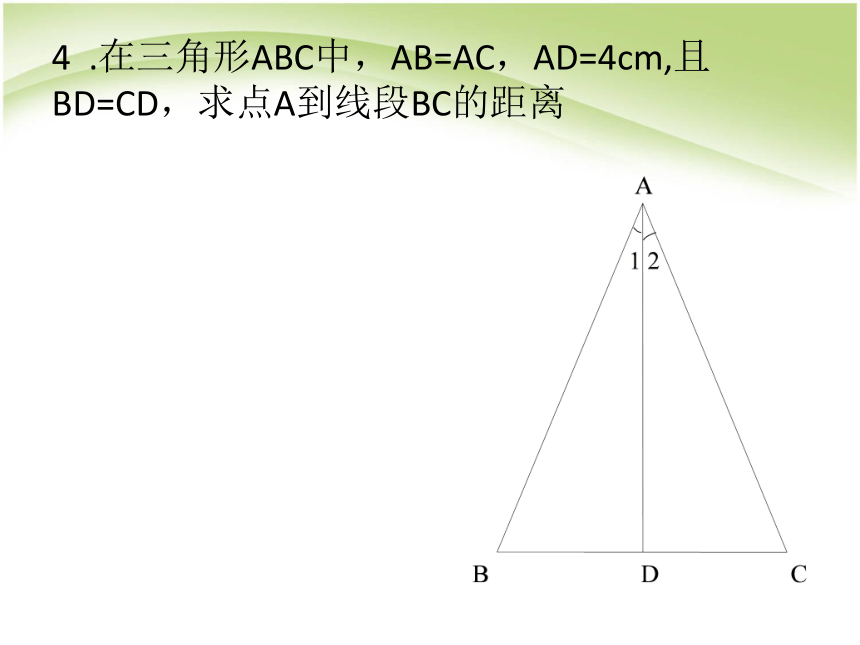
4 .在三角形ABC中,AB=AC,AD=4cm,且BD=CD,求点A到线段BC的距离
三、拓展训练
1、如图,△ABC中,AB=AD=DC,∠BAD=50°,求∠B、∠C的度数.
解:∵AB=AD=DC(已知)
∴ ∠B=∠ADB,
∠C=∠DAC(等边对等角)
∵∠BAD+∠B+∠ADB=180°(三角形内角等于180°)
∴∠B=∠ADB
= (180°—∠BAD) = ×(180°—50°)
=65°
∵∠ADB=∠C+∠DAC(三角形的一个外角等于与它不相邻的两个内角和)
∴∠C= ∠ADB
= ×65°
=32.5°
2、如图,已知∠EAC是△ABC的外角,∠1=∠2,AD∥BC,请说明AB=AC的理由。
理由:∵AD∥BC(已知)
∴∠B=∠1(两直线平行,同位角相等)
∠C=∠2(两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴∠B=∠C
∴AB=AC(等角对等边)
思想方法:转化思想
四、能力提升
1、已知:如图,在等腰△ABC中,AB=AC,O是底边BC上的中点,OD⊥AB于D,OE⊥AC于E.求证:AD=AE。
证明:∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵O是底边BC上的中点(已知)
∴OB=OC
∵OD⊥AB,OE⊥AC(已知)
∴∠ODB=∠OEC=90°
∴△BCE≌△ACD(AAS)
∴BD=CE(全等三角形对应边相等)
∴AB—BD=AC—CE
即AD=AE
Γ
Γ
2、如图 1,AD 是△ABC 的角平分线,BE⊥AD 交 AD 的延
长线于 E,EF∥AC 交 AB 于 F,求证:AF=FB.
图 1
∵BE⊥AE,
∴∠BEF+∠FEA=90°,∠ABE+∠BAD=90°.
∴∠ABE=∠FEB,
∴BF=EF,
∴AF=FB.
证明:∵AE 平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AC,∴∠CAD=∠AEF.
∴∠BAD=∠AEF,
∴AF=EF.
3、如图,在四边形ABCD中,∠ABC=∠ADC=90°,
M、N分别是AC、BD的中点,试说明:
(1)MD=MB;(2)MN⊥BD.
2.5 等腰三角形的轴对称性(3)
五、综合应用
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。
证明:①∵△ABC和△CDE都是等边三角形(已知)
∴BC=AC,CE=CD
∠BCF=∠HCD=60°(等边三角形三边相等,
三个角都等于60°)
∴∠BCF+∠FCH=∠HCD+∠FCH
即∠BCA=∠ACD
∴△BCE≌△ACD(SAS)
五、综合应用
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,①求证:△BCE≌△ACD;②求证:CF=CH;③判断△CFH的形状并说明理由
②∵△BCE≌△ACD
∴∠CBF=∠CAH(全等三角形对应角相等)
∵∠FCH=180°—∠BCF—∠HCD
=180°—60°—60°
=60°
∴∠BCF=∠FCH=60°
又∵BC=AC
∴△BCF≌△ACH(ASA)
∴CF=CH(全等三角形对应边相等)
③△CFH是等边三角形.
理由:∵CF=CH ,∠FCH=60°
∴△CFH是等边三角形.
六、补充练习
1、如图,已知P、Q是△ ABC边BC上的两点,且BP=PQ=QC=AP=AQ.求:∠ BAC的度数。
2、如图在△ABC中,AB=AC=8,BC=6,AF⊥BC,
BE⊥AC,垂足分别为点F、E,且点D是AB的中点,
△DEF周长是
蕴含知识点:
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
七、小结
通过本节课的复习,谈谈你有什么收获?
再见
等腰三角形的轴对称性
A
C
B
腰
腰
底边
顶角
底角
底角
一起回忆
一知识回顾
三角形 性质
判定
等腰三角形
等边三角形
1.等边对等角。
2.三线合一 。
3.轴对称图形。
1.等角对等边。
2.定义:两边等的三角形是等腰三角形。
1.三边相等。
2.三个角都相等,每个角都是60°。
3.轴对称图形。
1.有一个角是60°
的等腰三角形是
等边三角形。
2.三个角相等的
三角形是等边三
角形。
热身练习
1.填空
1)、等腰三角形的一个顶角是100 ,则它的底角是______。
2)、等腰三角形的一个底角是50 ,则它的顶角是______。
3)、等腰三角形的一个内角等于70°,则它的底角等于____。
4)、等腰三角形底边是4cm,腰长是6cm,则它的周长是_____ cm
5)、等腰三角形有两边长分别为3cm、4cm,则周长为 _____ 。
6)、等腰三角形有两边长分别为2cm、4cm,则周长为 _____cm。
40
70 或55
80
10
16cm
10cm或11cm
思想方法:分类讨论
2.判断题
1)、等腰三角形的角平分线、中线和高互相重合。( )
2)、有一个角是60°的等腰三角形其它两内角也60°。( )
3)、三角形的三个外角都相等的三角形是等边三角形。( )
4)、等腰三角形的底角都是锐角。 ( )
5)、钝角三角形不可能是等腰三角形 。 ( )
×
√
√
√
×
难点突破
1 三角形ABC中,已知AB=AC,且∠B=80° ,则∠C= 度,∠A= 度?
80
20
2.在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?
∟
2
4
3. 在三角形ABC中,AB=AC,且AD ⊥BC,已知∠ 1=20°,求∠ 2=_____度∠ BAC=______度?
∟
20
40
4 .在三角形ABC中,AB=AC,AD=4cm,且BD=CD,求点A到线段BC的距离
三、拓展训练
1、如图,△ABC中,AB=AD=DC,∠BAD=50°,求∠B、∠C的度数.
解:∵AB=AD=DC(已知)
∴ ∠B=∠ADB,
∠C=∠DAC(等边对等角)
∵∠BAD+∠B+∠ADB=180°(三角形内角等于180°)
∴∠B=∠ADB
= (180°—∠BAD) = ×(180°—50°)
=65°
∵∠ADB=∠C+∠DAC(三角形的一个外角等于与它不相邻的两个内角和)
∴∠C= ∠ADB
= ×65°
=32.5°
2、如图,已知∠EAC是△ABC的外角,∠1=∠2,AD∥BC,请说明AB=AC的理由。
理由:∵AD∥BC(已知)
∴∠B=∠1(两直线平行,同位角相等)
∠C=∠2(两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴∠B=∠C
∴AB=AC(等角对等边)
思想方法:转化思想
四、能力提升
1、已知:如图,在等腰△ABC中,AB=AC,O是底边BC上的中点,OD⊥AB于D,OE⊥AC于E.求证:AD=AE。
证明:∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵O是底边BC上的中点(已知)
∴OB=OC
∵OD⊥AB,OE⊥AC(已知)
∴∠ODB=∠OEC=90°
∴△BCE≌△ACD(AAS)
∴BD=CE(全等三角形对应边相等)
∴AB—BD=AC—CE
即AD=AE
Γ
Γ
2、如图 1,AD 是△ABC 的角平分线,BE⊥AD 交 AD 的延
长线于 E,EF∥AC 交 AB 于 F,求证:AF=FB.
图 1
∵BE⊥AE,
∴∠BEF+∠FEA=90°,∠ABE+∠BAD=90°.
∴∠ABE=∠FEB,
∴BF=EF,
∴AF=FB.
证明:∵AE 平分∠BAC,
∴∠BAD=∠CAD,
∵EF∥AC,∴∠CAD=∠AEF.
∴∠BAD=∠AEF,
∴AF=EF.
3、如图,在四边形ABCD中,∠ABC=∠ADC=90°,
M、N分别是AC、BD的中点,试说明:
(1)MD=MB;(2)MN⊥BD.
2.5 等腰三角形的轴对称性(3)
五、综合应用
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。
证明:①∵△ABC和△CDE都是等边三角形(已知)
∴BC=AC,CE=CD
∠BCF=∠HCD=60°(等边三角形三边相等,
三个角都等于60°)
∴∠BCF+∠FCH=∠HCD+∠FCH
即∠BCA=∠ACD
∴△BCE≌△ACD(SAS)
五、综合应用
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,①求证:△BCE≌△ACD;②求证:CF=CH;③判断△CFH的形状并说明理由
②∵△BCE≌△ACD
∴∠CBF=∠CAH(全等三角形对应角相等)
∵∠FCH=180°—∠BCF—∠HCD
=180°—60°—60°
=60°
∴∠BCF=∠FCH=60°
又∵BC=AC
∴△BCF≌△ACH(ASA)
∴CF=CH(全等三角形对应边相等)
③△CFH是等边三角形.
理由:∵CF=CH ,∠FCH=60°
∴△CFH是等边三角形.
六、补充练习
1、如图,已知P、Q是△ ABC边BC上的两点,且BP=PQ=QC=AP=AQ.求:∠ BAC的度数。
2、如图在△ABC中,AB=AC=8,BC=6,AF⊥BC,
BE⊥AC,垂足分别为点F、E,且点D是AB的中点,
△DEF周长是
蕴含知识点:
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.
七、小结
通过本节课的复习,谈谈你有什么收获?
再见
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
