6.10测量回顾与整理(课件)冀教版数学六年级下册(共17张PPT)
文档属性
| 名称 | 6.10测量回顾与整理(课件)冀教版数学六年级下册(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 15:16:39 | ||
图片预览






文档简介
(共17张PPT)
六年级下册
6.10测量回顾与整理
学习目标
1、系统地复习、整理计量单位和图形公式,回顾平面图形周长和面积公式、立体图形体积公式推导的过程。
2、进一步理解和掌握长度单位,面积单位、体积单位及其进率,掌握简单平面图形周长和面积计算公式,掌握长方体,正方体表面积的计算方法,掌握长方体、正方体、圆柱体和圆锥体的体积计算公式,能正确运用公式进行计算。
3、能用自己的语言表述相关公式的推导过程,理解公式之间的内在联系,进一步体会转化思想,发展学生的空间观念。
知识梳理
1、长方体的表面积 = ( )
2、正方体的表面积=( )
3、长方体的体积 =( ) 用字母表示( )
4、正方体的体积 = ( ) 用字母表示( )
5、长方体(或正方体)的体积=( ) 用字母表示( )
(长×宽+长×高+宽×高)×2
棱长×棱长×6
长×宽×高
V=abh
棱长×棱长×棱长
V=a3
底面积×高
V=sh
知识梳理
6、长方体或正方体容器容积的计算方法与体积的计算方法相同,但要从容器( )量长、宽、高。
7、圆柱的侧面积=( )×( )。
8、圆柱的体积=( )×( ),用字母表示为( )。
9、圆锥的体积等于和它( )的圆柱体积的 。用字母表示为( )。
里面
底面周长
高
底面积
高
V=Sh
等底等高
V= Sh
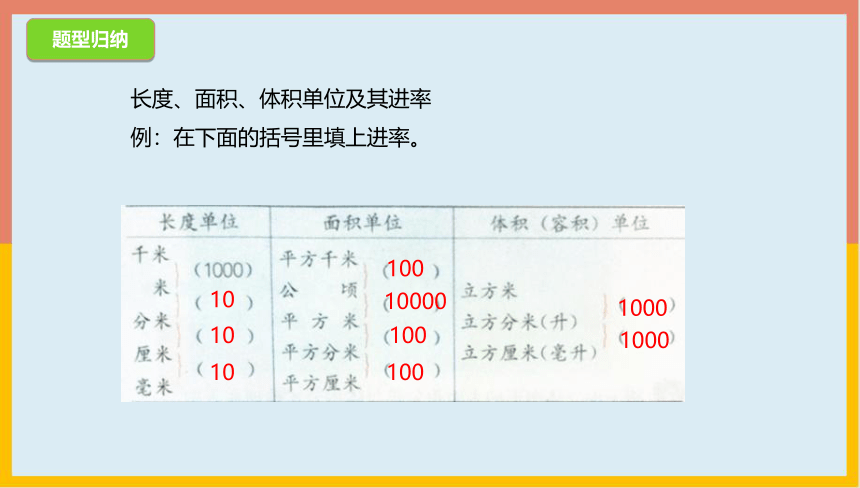
长度、面积、体积单位及其进率
例:在下面的括号里填上进率。
题型归纳
10
10
10
100
10000
100
100
1000
1000
2、图形的周长公式与面积公式。
例:将下面的图形的周长公式与面积公式整理在表中。说说下面各图形的面积公式是怎样推导出来的。
题型归纳
c=(a+b)×2
S=ab
c=4a
S=a2
S=ah÷2
S=ah
S=(a+b)h÷2
S=πr2
c=πd=2πr
3、立体图形公式
例:将下面立体图形的表面积公式与体积公式整理在表中。
题型归纳
S=(ab+ah+bh)×2
V=abh
S=6a2
V=a3
S=2πrh+2πr2
V=πr2h
V= πr2h
本课小结
A
长度的计量单位:千米、米、分米、厘米、毫米;面积单位:平方千米、公顷、平方米、平方分米、平方厘米;体积单位:立方米、立方分米、立方厘米
B
三角形的面积和梯形的面积计算公式是根据平行四边形的面积计算公式推导出来的;平行四边形和圆的面积计算公式都是根据长方形的面积计算公式推导出来。
C
圆柱的体积计算公式是根据长方体的体积计算公式推导出来;圆锥的体积等于和它等底等高的圆柱体积的 。
测量回顾与整理
随堂检测
1、用同样大小的方格拼成了图形A和B,其中,图形A的周长是48厘米,图形B的周长是多少厘米?
60厘米
随堂检测
2、下面每个方格表示1平方厘米,试着估算方格图中曲线所围部分的面积。
42平方厘米
随堂检测
3、求下面各图涂色部分的面积。(单位:cm)
15×8-3.14×(8÷2)2÷2
=120-25.12
=94.88(平方厘米)
9×4.5-9×4.5÷2
=40.5-20.25
=20.25(平方厘米)
随堂检测
3、求下面各图涂色部分的面积。(单位:cm)
(9+16)×4÷2+9×2-3.14×(2÷2)2
=50+18-3.14
=64.86(平方厘米)
3.14×(20÷2)2-3.14×(10÷2)2
=314-78.5
=235.5(平方厘米)
随堂检测
4、计算下面各立体图形的体积。
1.5×1×0.3=0.45(立方米)
4×4×4=64(立方厘米)
3.14×(4÷2)2×6=75.36(立方分米)
×3.14×(12÷2)2×15=565.2(立方厘米)
随堂检测
5、(1)做下面两个无盖鱼缸,每个鱼缸至少需要玻璃多少平方分米?
(70×60+60×50)×2+70×50
=(4200+3000)×2+3500
=179000(平方厘米)
=176(平方分米)
60×60×5=180000(平方厘米)=180(平方分米)
随堂检测
5、(2)如果把鱼缸都装满水,哪个鱼缸盛水多,多多少升?
60×60×60-70×60×50
=216000-210000
=6000(立方厘米)
=6(升)
答:多6升。
作业布置
1、水泥制品厂签订了一份生产1200节水泥管的合同,生产之前至少应准备多少立方米的混凝土?
2、预习第74、75页的有关内容。
空白演示
单击输入您的封面副标题
谢 谢 聆 听
六年级下册
6.10测量回顾与整理
学习目标
1、系统地复习、整理计量单位和图形公式,回顾平面图形周长和面积公式、立体图形体积公式推导的过程。
2、进一步理解和掌握长度单位,面积单位、体积单位及其进率,掌握简单平面图形周长和面积计算公式,掌握长方体,正方体表面积的计算方法,掌握长方体、正方体、圆柱体和圆锥体的体积计算公式,能正确运用公式进行计算。
3、能用自己的语言表述相关公式的推导过程,理解公式之间的内在联系,进一步体会转化思想,发展学生的空间观念。
知识梳理
1、长方体的表面积 = ( )
2、正方体的表面积=( )
3、长方体的体积 =( ) 用字母表示( )
4、正方体的体积 = ( ) 用字母表示( )
5、长方体(或正方体)的体积=( ) 用字母表示( )
(长×宽+长×高+宽×高)×2
棱长×棱长×6
长×宽×高
V=abh
棱长×棱长×棱长
V=a3
底面积×高
V=sh
知识梳理
6、长方体或正方体容器容积的计算方法与体积的计算方法相同,但要从容器( )量长、宽、高。
7、圆柱的侧面积=( )×( )。
8、圆柱的体积=( )×( ),用字母表示为( )。
9、圆锥的体积等于和它( )的圆柱体积的 。用字母表示为( )。
里面
底面周长
高
底面积
高
V=Sh
等底等高
V= Sh
长度、面积、体积单位及其进率
例:在下面的括号里填上进率。
题型归纳
10
10
10
100
10000
100
100
1000
1000
2、图形的周长公式与面积公式。
例:将下面的图形的周长公式与面积公式整理在表中。说说下面各图形的面积公式是怎样推导出来的。
题型归纳
c=(a+b)×2
S=ab
c=4a
S=a2
S=ah÷2
S=ah
S=(a+b)h÷2
S=πr2
c=πd=2πr
3、立体图形公式
例:将下面立体图形的表面积公式与体积公式整理在表中。
题型归纳
S=(ab+ah+bh)×2
V=abh
S=6a2
V=a3
S=2πrh+2πr2
V=πr2h
V= πr2h
本课小结
A
长度的计量单位:千米、米、分米、厘米、毫米;面积单位:平方千米、公顷、平方米、平方分米、平方厘米;体积单位:立方米、立方分米、立方厘米
B
三角形的面积和梯形的面积计算公式是根据平行四边形的面积计算公式推导出来的;平行四边形和圆的面积计算公式都是根据长方形的面积计算公式推导出来。
C
圆柱的体积计算公式是根据长方体的体积计算公式推导出来;圆锥的体积等于和它等底等高的圆柱体积的 。
测量回顾与整理
随堂检测
1、用同样大小的方格拼成了图形A和B,其中,图形A的周长是48厘米,图形B的周长是多少厘米?
60厘米
随堂检测
2、下面每个方格表示1平方厘米,试着估算方格图中曲线所围部分的面积。
42平方厘米
随堂检测
3、求下面各图涂色部分的面积。(单位:cm)
15×8-3.14×(8÷2)2÷2
=120-25.12
=94.88(平方厘米)
9×4.5-9×4.5÷2
=40.5-20.25
=20.25(平方厘米)
随堂检测
3、求下面各图涂色部分的面积。(单位:cm)
(9+16)×4÷2+9×2-3.14×(2÷2)2
=50+18-3.14
=64.86(平方厘米)
3.14×(20÷2)2-3.14×(10÷2)2
=314-78.5
=235.5(平方厘米)
随堂检测
4、计算下面各立体图形的体积。
1.5×1×0.3=0.45(立方米)
4×4×4=64(立方厘米)
3.14×(4÷2)2×6=75.36(立方分米)
×3.14×(12÷2)2×15=565.2(立方厘米)
随堂检测
5、(1)做下面两个无盖鱼缸,每个鱼缸至少需要玻璃多少平方分米?
(70×60+60×50)×2+70×50
=(4200+3000)×2+3500
=179000(平方厘米)
=176(平方分米)
60×60×5=180000(平方厘米)=180(平方分米)
随堂检测
5、(2)如果把鱼缸都装满水,哪个鱼缸盛水多,多多少升?
60×60×60-70×60×50
=216000-210000
=6000(立方厘米)
=6(升)
答:多6升。
作业布置
1、水泥制品厂签订了一份生产1200节水泥管的合同,生产之前至少应准备多少立方米的混凝土?
2、预习第74、75页的有关内容。
空白演示
单击输入您的封面副标题
谢 谢 聆 听
