北师大版七年级下册4.3探索三角形全等的条件 课件(共22张PPT)
文档属性
| 名称 | 北师大版七年级下册4.3探索三角形全等的条件 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 851.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 08:40:42 | ||
图片预览




文档简介
(共22张PPT)
一、
情境引入
我也想要一个一模一样的
4.3探索三角形全等的条件1
教材版本:北师版七年级数学下册
β
π
Φ
∑
二、
温故知新
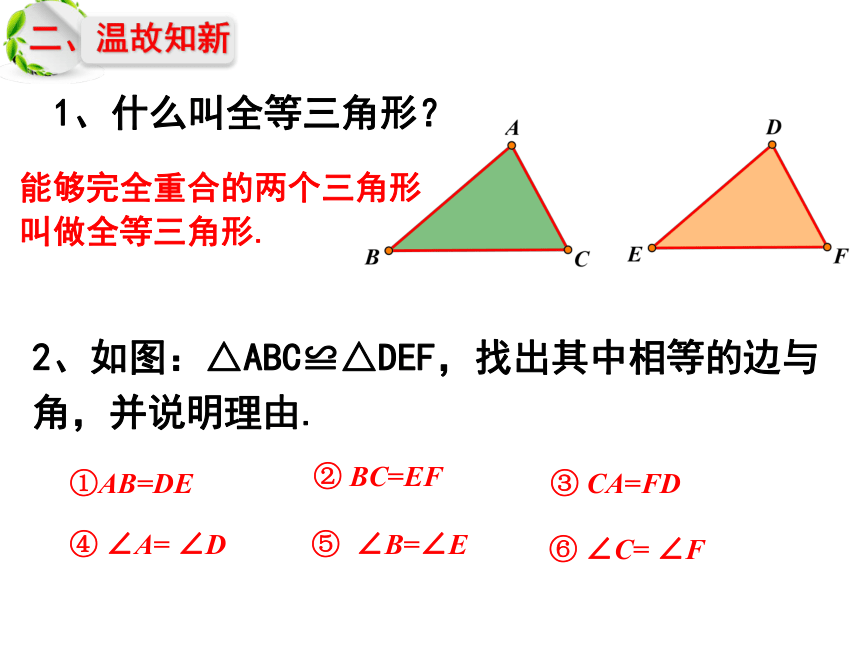
1、什么叫全等三角形?
2、如图:△ABC≌△DEF,找出其中相等的边与角,并说明理由.
能够完全重合的两个三角形叫做全等三角形.
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
生活问题
(做风筝)
数学问题
(全等三角形)
转化
思考:要画一个和已知三角形全等的三角形,一定需要定义中提出的六个条件吗?能否尽可能少呢?
两个条件
(1) 三角形的一个角 ,一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
一个条件
(1)有一条边对应相等的三角形
(2)有一个角对应相等的三角形
只给出两个条件时,不能保证所画的三角形一定全等.
只给出一个条件时,不能保证所画的三角形一定全等.
三、
探究新知
三个角对应相等
2. 三条边对应相等
3.一条边和两个角对应相等
三个角对应相等的三角形不一定全等
三个条件
4.两条边和一个角对应相等
三、
探究新知
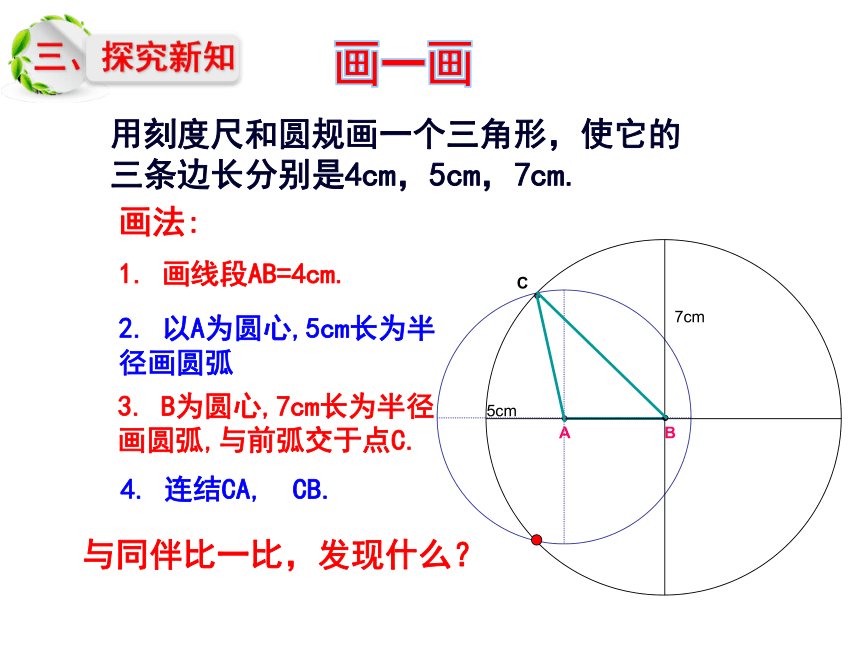
画一画
用刻度尺和圆规画一个三角形,使它的三条边长分别是4cm,5cm,7cm.
1. 画线段AB=4cm.
画法:
2. 以A为圆心,5cm长为半径画圆弧
4. 连结CA, CB.
与同伴比一比,发现什么?
A B
5cm
C
7cm
3. B为圆心,7cm长为半径画圆弧,与前弧交于点C.
三、
探究新知
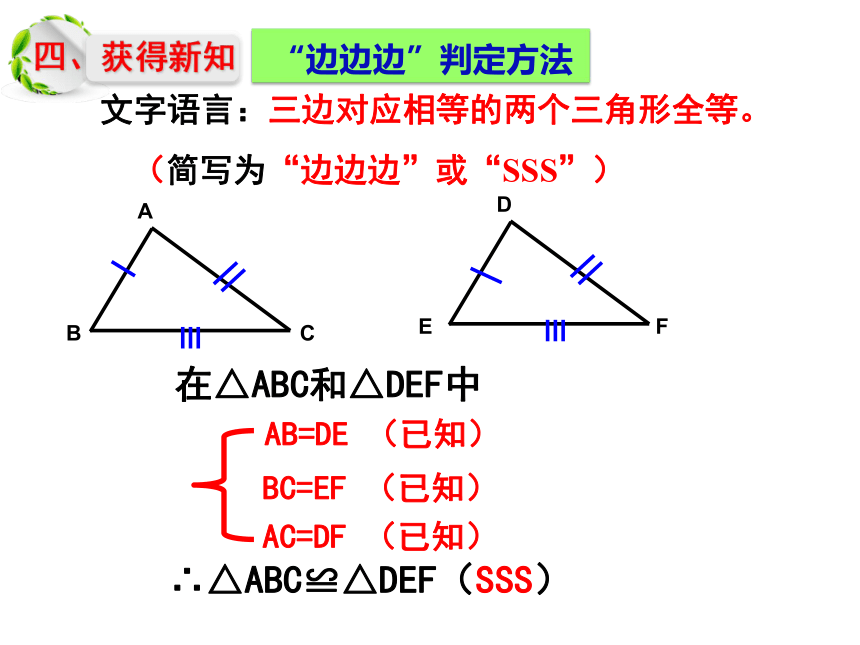
AB=DE (已知)
BC=EF (已知)
AC=DF (已知)
D
E
F
A
B
C
在△ABC和△DEF中
∴△ABC≌△DEF(SSS)
文字语言:三边对应相等的两个三角形全等。
(简写为“边边边”或“SSS”)
“边边边”判定方法
四、
获得新知
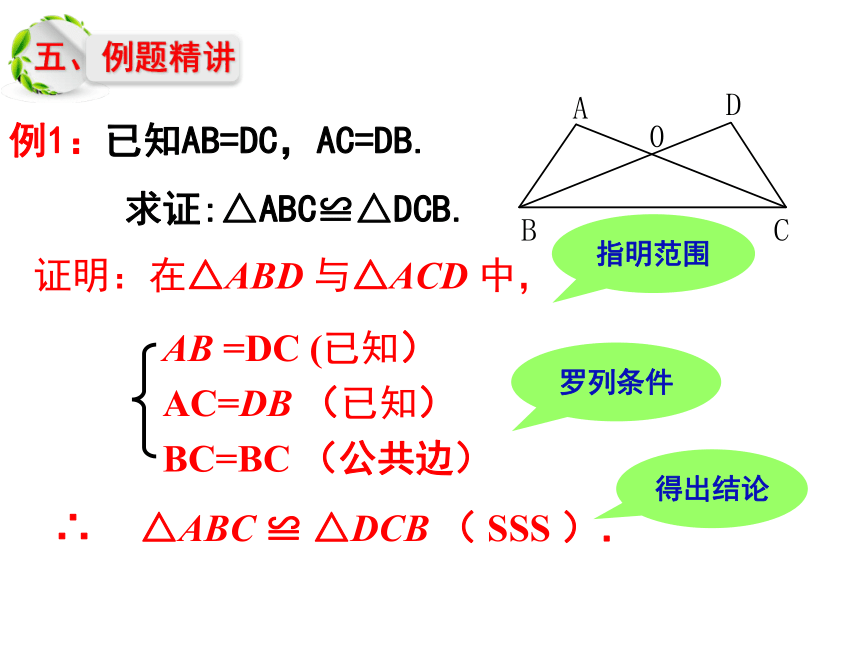
证明:在△ABD 与△ACD 中,
∴ △ABC ≌ △DCB ( SSS ).
AB =DC (已知)
AC=DB (已知)
BC=BC (公共边)
例1:已知AB=DC,AC=DB.
求证:△ABC≌△DCB.
指明范围
罗列条件
得出结论
五、
例题精讲
1.如图,D、F是线段BC上的两点,AB=CE,AF=DE,要使△ABF≌△ECD ,还需要条件 .
A
E
=
=
×
×
B
D
F
C
BF=CD
或 BD=FC
变式:
∵ BD=FC
∴ BD+DF=FC+DF
即:BF=CD(等式的性质)
例2:已知:如图 ,AC=FE,AD=FB,BC=DE.
求证:(1)△ABC≌△FDE; (2) ∠C= ∠E.
证明:(1)∵ AD=FB
∴ AD+BD=FB+BD
即:AB=FD(等式的性质) 在△ABC和△FDE
AC=FE(已知)
BC=DE(已知)
AB=FD(已证)
∴△ABC≌△FDE(SSS)
A
C
E
D
B
F
=
=
。
。
(2)∵ △ABC≌△FDE(已证)
∴ ∠C=∠E(全等三角形的对应角相等)
变式:已知AB=CD,BF=CE,AE=DF.
求证:(1)△ABE≌△DCF; (2)AB∥CD
证明:(1)∵ BF=CE
∴BF-EF=CE-EF
AC=FE(已知)
BC=DE(已知)
AB=FD(已证)
∴△ABC≌△FDE(SSS)
即BE=CF(等式的性质)
在△ABC和△FDE
(2)∵ △ABE≌△DCF(已证)
∴ ∠B=∠C(全等三角形的对应角相等)
∴ AB∥CD(内错角相等,两直线平行)
已知: 如图, 四边形ABCD中,AD=CB,AB=CD,
试说明: ∠A= ∠C。
A
C
D
B
分析:要证两角或两线段相等,先证这两角或两线段所在的两三角形全等,从而需构造全等三角形。
构造公共边是常添的辅助线
试说明:∠B=∠D
六、
思维提升
做一做
七、
联系生活
根据“SSS”,只要三角形三边的长度确定了,这个三形的形状和大小就确定,三角形的这个性质叫三角形的稳定性.
三角形的形状和大小是固定不变的,而四边形的
会改变。
用硬纸制作三角形和四边形框架,并拉动它们,你发现了什么?
八、
课堂总结
“边边边”
应用思路
数学思想
三角形稳定性
分类讨论思想
准备条件
已知条件
隐含条件
分析
公共边
辅助线
转化思想
数形结合思想
三角形全等的条件1
“边边边”
应用思路
数学思想
(1)有一条边对应相等
的三角形
(2)有一个角对应相等
的三角形
一角为40o
一边长5cm
A
B
5cm
40o
只给出一个条件时,不能保证所画的三角形
一定全等.
一个条件
两个条件
(1) 一个角和
一条边
对应相等
(2) 两条边 对应相等
(3) 两个角
对应相等
一内角30o ,一条边为3cm
两条边长分别为4cm、6cm
两个内角分别为40o、60o
A
B
30o
3cm
4cm
4cm
C1
C2
C
6cm
A
B
4cm
C
C1
C2
40o
60o
只给出两个条件时,不能保证所画的三角形
一定全等.
三个条件
三个角对应相等的三角形
三个角对应相等的三角形不一定全等
40o
60o
80o
40o
60o
感谢聆听
THANK YOU FOR YOUR ATTENTION
一、
情境引入
我也想要一个一模一样的
4.3探索三角形全等的条件1
教材版本:北师版七年级数学下册
β
π
Φ
∑
二、
温故知新
1、什么叫全等三角形?
2、如图:△ABC≌△DEF,找出其中相等的边与角,并说明理由.
能够完全重合的两个三角形叫做全等三角形.
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
生活问题
(做风筝)
数学问题
(全等三角形)
转化
思考:要画一个和已知三角形全等的三角形,一定需要定义中提出的六个条件吗?能否尽可能少呢?
两个条件
(1) 三角形的一个角 ,一条边对应相等
(2)三角形的两条边对应相等
(3)三角形的两个角对应相等
一个条件
(1)有一条边对应相等的三角形
(2)有一个角对应相等的三角形
只给出两个条件时,不能保证所画的三角形一定全等.
只给出一个条件时,不能保证所画的三角形一定全等.
三、
探究新知
三个角对应相等
2. 三条边对应相等
3.一条边和两个角对应相等
三个角对应相等的三角形不一定全等
三个条件
4.两条边和一个角对应相等
三、
探究新知
画一画
用刻度尺和圆规画一个三角形,使它的三条边长分别是4cm,5cm,7cm.
1. 画线段AB=4cm.
画法:
2. 以A为圆心,5cm长为半径画圆弧
4. 连结CA, CB.
与同伴比一比,发现什么?
A B
5cm
C
7cm
3. B为圆心,7cm长为半径画圆弧,与前弧交于点C.
三、
探究新知
AB=DE (已知)
BC=EF (已知)
AC=DF (已知)
D
E
F
A
B
C
在△ABC和△DEF中
∴△ABC≌△DEF(SSS)
文字语言:三边对应相等的两个三角形全等。
(简写为“边边边”或“SSS”)
“边边边”判定方法
四、
获得新知
证明:在△ABD 与△ACD 中,
∴ △ABC ≌ △DCB ( SSS ).
AB =DC (已知)
AC=DB (已知)
BC=BC (公共边)
例1:已知AB=DC,AC=DB.
求证:△ABC≌△DCB.
指明范围
罗列条件
得出结论
五、
例题精讲
1.如图,D、F是线段BC上的两点,AB=CE,AF=DE,要使△ABF≌△ECD ,还需要条件 .
A
E
=
=
×
×
B
D
F
C
BF=CD
或 BD=FC
变式:
∵ BD=FC
∴ BD+DF=FC+DF
即:BF=CD(等式的性质)
例2:已知:如图 ,AC=FE,AD=FB,BC=DE.
求证:(1)△ABC≌△FDE; (2) ∠C= ∠E.
证明:(1)∵ AD=FB
∴ AD+BD=FB+BD
即:AB=FD(等式的性质) 在△ABC和△FDE
AC=FE(已知)
BC=DE(已知)
AB=FD(已证)
∴△ABC≌△FDE(SSS)
A
C
E
D
B
F
=
=
。
。
(2)∵ △ABC≌△FDE(已证)
∴ ∠C=∠E(全等三角形的对应角相等)
变式:已知AB=CD,BF=CE,AE=DF.
求证:(1)△ABE≌△DCF; (2)AB∥CD
证明:(1)∵ BF=CE
∴BF-EF=CE-EF
AC=FE(已知)
BC=DE(已知)
AB=FD(已证)
∴△ABC≌△FDE(SSS)
即BE=CF(等式的性质)
在△ABC和△FDE
(2)∵ △ABE≌△DCF(已证)
∴ ∠B=∠C(全等三角形的对应角相等)
∴ AB∥CD(内错角相等,两直线平行)
已知: 如图, 四边形ABCD中,AD=CB,AB=CD,
试说明: ∠A= ∠C。
A
C
D
B
分析:要证两角或两线段相等,先证这两角或两线段所在的两三角形全等,从而需构造全等三角形。
构造公共边是常添的辅助线
试说明:∠B=∠D
六、
思维提升
做一做
七、
联系生活
根据“SSS”,只要三角形三边的长度确定了,这个三形的形状和大小就确定,三角形的这个性质叫三角形的稳定性.
三角形的形状和大小是固定不变的,而四边形的
会改变。
用硬纸制作三角形和四边形框架,并拉动它们,你发现了什么?
八、
课堂总结
“边边边”
应用思路
数学思想
三角形稳定性
分类讨论思想
准备条件
已知条件
隐含条件
分析
公共边
辅助线
转化思想
数形结合思想
三角形全等的条件1
“边边边”
应用思路
数学思想
(1)有一条边对应相等
的三角形
(2)有一个角对应相等
的三角形
一角为40o
一边长5cm
A
B
5cm
40o
只给出一个条件时,不能保证所画的三角形
一定全等.
一个条件
两个条件
(1) 一个角和
一条边
对应相等
(2) 两条边 对应相等
(3) 两个角
对应相等
一内角30o ,一条边为3cm
两条边长分别为4cm、6cm
两个内角分别为40o、60o
A
B
30o
3cm
4cm
4cm
C1
C2
C
6cm
A
B
4cm
C
C1
C2
40o
60o
只给出两个条件时,不能保证所画的三角形
一定全等.
三个条件
三个角对应相等的三角形
三个角对应相等的三角形不一定全等
40o
60o
80o
40o
60o
感谢聆听
THANK YOU FOR YOUR ATTENTION
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
