华东师大版七下数学6.2.1等式的性质和方程的简单变形 课件(34张ppt)
文档属性
| 名称 | 华东师大版七下数学6.2.1等式的性质和方程的简单变形 课件(34张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 590.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 09:06:50 | ||
图片预览



文档简介
(共34张PPT)
6.2.1等式的性质 和方程的简单变形
知识回顾
(1)1+2+3+4=10
1.指出下列式子中哪些是方程?哪些不是?
(2)2x-3
(3)1+0.5x=9
(4)2x-3>0
(5)x+y=1
2.我们班在本学期新转进5人,现在共有40人,则原来有多少人?怎样列方程?
新课导入
a
你能发现什么规律?
右
左
a
b
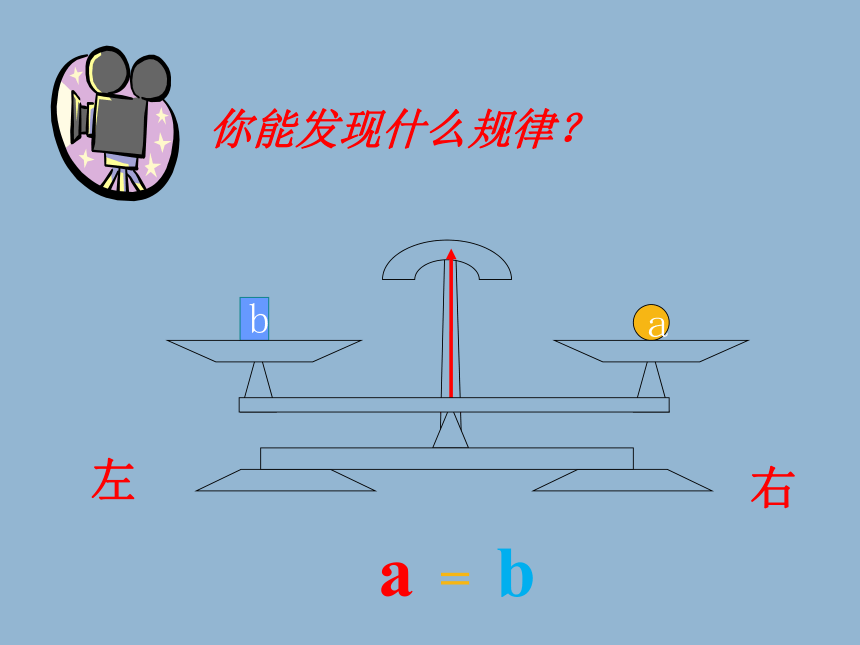
你能发现什么规律?
右
左
b
a
你能发现什么规律?
右
左
b
a
你能发现什么规律?
右
左
b
a
你能发现什么规律?
右
左
a = b
b
a
你能发现什么规律?
c
右
左
c
b
a
你能发现什么规律?
右
左
a
c
b
你能发现什么规律?
右
左
c
b
c
a
你能发现什么规律?
右
左
c
b
c
a
你能发现什么规律?
a+c
=
右
左
b+c
c
b
c
a
你能发现什么规律?
右
左
a
c
b
你能发现什么规律?
右
左
b
a
你能发现什么规律?
右
左
b
a
你能发现什么规律?
右
左
等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式。
等式的基本性质1
b
a
你能发现什么规律?
右
左
a
b
2a = 2b
b
a
你能发现什么规律?
右
左
b
b
a
a
3a = 3b
b
a
你能发现什么规律?
右
左
b
b
a
a
等式的两边都乘以(或除以)同一个数(除数不为零),所得结果仍是等式。
等式的基本性质2
1.回答下列问题:
(1)由a=b能不能得到a-2=b-2?为什么?
(2)由m=n能不能得到-m/3=-n/3 为什么?
(3)由2a=6b能不能得到a=3b 为什么?
(4)由x/2=y/3能不能得到3x=2y 为什么?
2.填空,使所得结果仍是等式,并说明是根据哪一条等式性质得到的:
(2)如果3x=10-2x,那么3x+ =10,
根据
2
等式的基本性质1
(1)如果x-2=5,那么x=5+ 根据
(3)如果2x=7,那么x= 根据
(4)如果x/2=3,那么x= 根据
2x
等式的基本性质1
7/2
等式的基本性质2
6
等式的基本性质2
1、方程的两边都加上或都减去同一个数或同一个整式,方程的解不变。
2、方程的两边都乘以或除以同一个不为零的数,方程的解不变。
方程的变形规则:
解下列方程
(1)x-5=7
(2)4x=3x-4
将方程中的某些项改变符号后,从方程的一边移到另一边的变形叫做移项.
注意:移项要变号
小结:
例1
①从5+y=7,得到y =7+5
②从9x =8+8x,得到9x-8x=8
③从y-2=2y+3,得到2y-y=3+2
下列的移项是否正确?
思考
解下列方程
1、x + 2 = 8;
2、3x+3=2x+7;
巩固练习
解下列方程
(1)-5x = 20
(2)
3
—
2
1
3
—
X=
将方程的两边都除以未知数的系数,这样的变形通常称作“将未知数的系数化为1”。
例2
小结:
分子分母别颠倒!
注意:
尝试
解下列方程
(1)-4x = 20
(2)
3
—
4
x =
1
__
3
解下列方程
1、2x = - 4;
巩固练习
2、2x + 6 = 2;
1.已知方程5x=4x,根据___________,
方程两边都_______ ,得 x=0。
2.已知方程5y/2=1/3,根据 _______ ,
方程两边都______,得15y=2,方程两边都________,得y=2/15。
变形规则1
变形规则2
减去4x
乘以6
除以15
填空题
练
利用方程的变形规则,在括号内填上适当的数或式。
1、5x=-x+5
2、6x-4=4
3、-3x=6
4、0.5y+7=5
5x+______=5。
6x=______,x=_____。
X=______。
0.5y=_____,y=____。
x
8
4
3
-2
-2
-4
再见
6.2.1等式的性质 和方程的简单变形
知识回顾
(1)1+2+3+4=10
1.指出下列式子中哪些是方程?哪些不是?
(2)2x-3
(3)1+0.5x=9
(4)2x-3>0
(5)x+y=1
2.我们班在本学期新转进5人,现在共有40人,则原来有多少人?怎样列方程?
新课导入
a
你能发现什么规律?
右
左
a
b
你能发现什么规律?
右
左
b
a
你能发现什么规律?
右
左
b
a
你能发现什么规律?
右
左
b
a
你能发现什么规律?
右
左
a = b
b
a
你能发现什么规律?
c
右
左
c
b
a
你能发现什么规律?
右
左
a
c
b
你能发现什么规律?
右
左
c
b
c
a
你能发现什么规律?
右
左
c
b
c
a
你能发现什么规律?
a+c
=
右
左
b+c
c
b
c
a
你能发现什么规律?
右
左
a
c
b
你能发现什么规律?
右
左
b
a
你能发现什么规律?
右
左
b
a
你能发现什么规律?
右
左
等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式。
等式的基本性质1
b
a
你能发现什么规律?
右
左
a
b
2a = 2b
b
a
你能发现什么规律?
右
左
b
b
a
a
3a = 3b
b
a
你能发现什么规律?
右
左
b
b
a
a
等式的两边都乘以(或除以)同一个数(除数不为零),所得结果仍是等式。
等式的基本性质2
1.回答下列问题:
(1)由a=b能不能得到a-2=b-2?为什么?
(2)由m=n能不能得到-m/3=-n/3 为什么?
(3)由2a=6b能不能得到a=3b 为什么?
(4)由x/2=y/3能不能得到3x=2y 为什么?
2.填空,使所得结果仍是等式,并说明是根据哪一条等式性质得到的:
(2)如果3x=10-2x,那么3x+ =10,
根据
2
等式的基本性质1
(1)如果x-2=5,那么x=5+ 根据
(3)如果2x=7,那么x= 根据
(4)如果x/2=3,那么x= 根据
2x
等式的基本性质1
7/2
等式的基本性质2
6
等式的基本性质2
1、方程的两边都加上或都减去同一个数或同一个整式,方程的解不变。
2、方程的两边都乘以或除以同一个不为零的数,方程的解不变。
方程的变形规则:
解下列方程
(1)x-5=7
(2)4x=3x-4
将方程中的某些项改变符号后,从方程的一边移到另一边的变形叫做移项.
注意:移项要变号
小结:
例1
①从5+y=7,得到y =7+5
②从9x =8+8x,得到9x-8x=8
③从y-2=2y+3,得到2y-y=3+2
下列的移项是否正确?
思考
解下列方程
1、x + 2 = 8;
2、3x+3=2x+7;
巩固练习
解下列方程
(1)-5x = 20
(2)
3
—
2
1
3
—
X=
将方程的两边都除以未知数的系数,这样的变形通常称作“将未知数的系数化为1”。
例2
小结:
分子分母别颠倒!
注意:
尝试
解下列方程
(1)-4x = 20
(2)
3
—
4
x =
1
__
3
解下列方程
1、2x = - 4;
巩固练习
2、2x + 6 = 2;
1.已知方程5x=4x,根据___________,
方程两边都_______ ,得 x=0。
2.已知方程5y/2=1/3,根据 _______ ,
方程两边都______,得15y=2,方程两边都________,得y=2/15。
变形规则1
变形规则2
减去4x
乘以6
除以15
填空题
练
利用方程的变形规则,在括号内填上适当的数或式。
1、5x=-x+5
2、6x-4=4
3、-3x=6
4、0.5y+7=5
5x+______=5。
6x=______,x=_____。
X=______。
0.5y=_____,y=____。
x
8
4
3
-2
-2
-4
再见
