2021—2022学年湘教版九年级数学下册1.5二次函数的应用 同步练习 (Word版含答案)
文档属性
| 名称 | 2021—2022学年湘教版九年级数学下册1.5二次函数的应用 同步练习 (Word版含答案) | 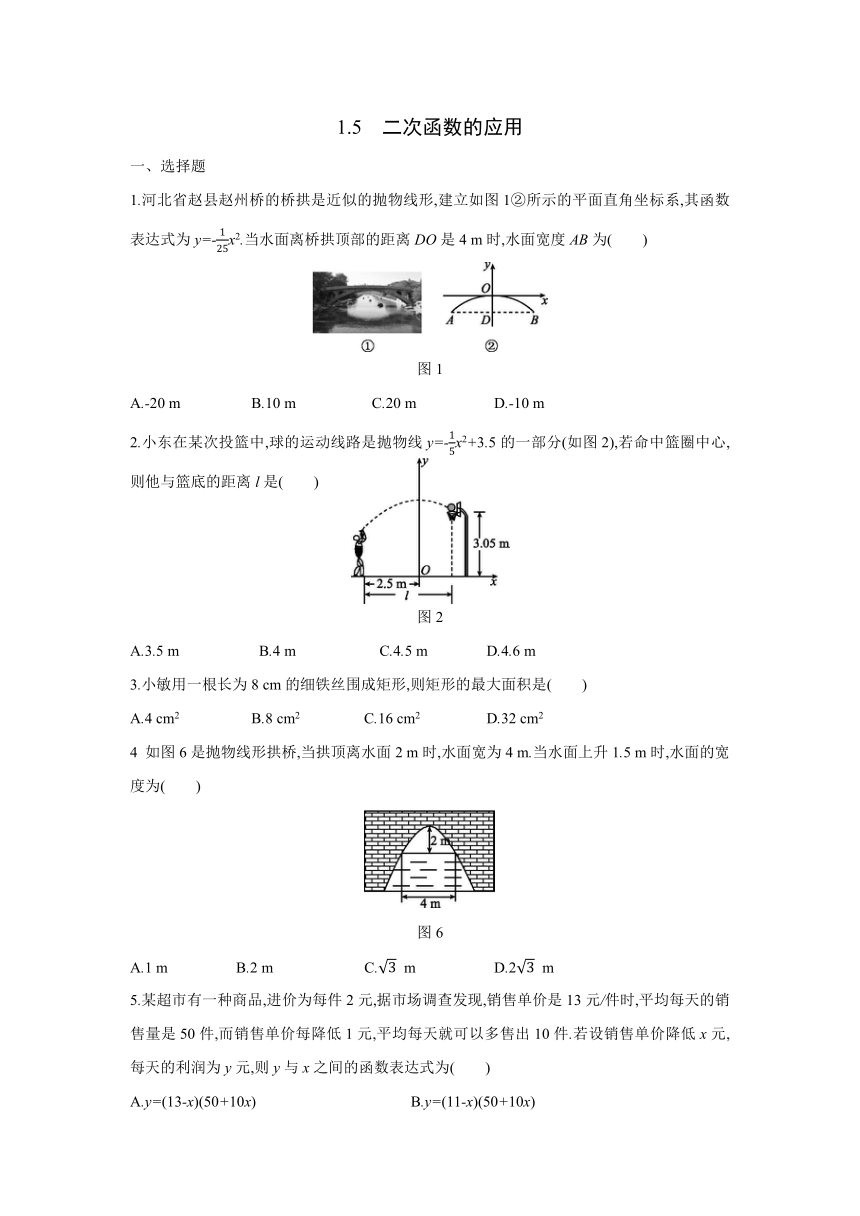 | |
| 格式 | docx | ||
| 文件大小 | 131.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 09:12:58 | ||
图片预览




文档简介
1.5 二次函数的应用
一、选择题
1.河北省赵县赵州桥的桥拱是近似的抛物线形,建立如图1②所示的平面直角坐标系,其函数表达式为y=-x2.当水面离桥拱顶部的距离DO是4 m时,水面宽度AB为( )
图1
A.-20 m B.10 m C.20 m D.-10 m
2.小东在某次投篮中,球的运动线路是抛物线y=-x2+3.5的一部分(如图2),若命中篮圈中心,则他与篮底的距离l是( )
图2
A.3.5 m B.4 m C.4.5 m D.4.6 m
3.小敏用一根长为8 cm的细铁丝围成矩形,则矩形的最大面积是( )
A.4 cm2 B.8 cm2 C.16 cm2 D.32 cm2
4 如图6是抛物线形拱桥,当拱顶离水面2 m时,水面宽为4 m.当水面上升1.5 m时,水面的宽度为( )
图6
A.1 m B.2 m C. m D.2 m
5.某超市有一种商品,进价为每件2元,据市场调查发现,销售单价是13元/件时,平均每天的销售量是50件,而销售单价每降低1元,平均每天就可以多售出10件.若设销售单价降低x元,每天的利润为y元,则y与x之间的函数表达式为( )
A.y=(13-x)(50+10x) B.y=(11-x)(50+10x)
C.y=(2-x)(50+10x) D.y=(11-x)(50+x)
6.服装店将进价为100元/件的服装按x元/件出售,每天可销售(200-x)件.规定售价不低于进价.若想获得最大利润,则x的值为( )
A.150 B.160 C.170 D.180
7 竖直向上抛的物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=-5t2+v0t+h0表示,其中h0(m)是物体抛出时离地面的高度,v0(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5 m的高处以20 m/s的速度竖直向上抛出,小球达到的离地面的最大高度为( )
A.23.5 m B.22.5 m C.21.5 m D.20.5 m
8.广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠与喷头的水平距离x(米)的函数表达式是y=-x2+6x(0≤x≤4),那么水珠的高度达到最大时,水珠与喷头的水平距离是( )
A.1米 B.2米 C.5米 D.6米
9. 某商店销售某件商品所获得的利润y(元)与所卖的件数x之间的关系满足y=-x2+1000x-200000,则当0A.2500元 B.47500元 C.50000元 D.250000元
填空题
10.如图4,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,点P以2 cm/s的速度从点A开始沿AB向点B运动,点Q以1 cm/s的速度从点B开始沿BC向点C运动,如果点P,Q分别从点A,B同时出发,当△PBQ的面积最大时,运动时间为 s.
图4
11.某农场拟建两间矩形饲养室,一面靠在足够长的墙体上,中间用一道围栏隔开,并在如图7所示的两处各留1 m宽的门,所有围栏的总长(不含门)为26 m,若要使得建成的饲养室面积最大,则利用墙体的长度为 m.
图7
12.已知商场某商品的进价为每件40元,现在的销售单价是60元/件,一周内可卖出300件.市场调查反映:售价每件每涨价1元,一周内要少卖出10件商品.设售价每件涨价x元,当x=
时,商场能在一周内获得最大利润.
13.加工爆米花时,爆开且不煳的粒数的百分比称为“可食用率”.在特定条件下,可食用率y与加工时间x(单位:min)满足函数表达式y=-0.2x2+1.5x-2,则最佳加工时间为
min.
14.某商场购进一批单价为20元/件的日用商品,如果以30元/件的价格出售,那么半月内可售出400件.根据销售经验,提高销售单价会导致销售量减少,即销售单价每提高1元,半月内销售量将减少20件.当销售单价是 元/件时,该商场才能在半月内获得最大利润.
三、计算题
15.某工厂的大门是一抛物线水泥建筑物,大门地面宽AB为4 m,顶部C离地面高为4.4 m,以AB所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图3所示.
(1)求该抛物线所表示的函数表达式;
(2)现有一辆载满货物的汽车欲通过大门,货物顶端距地面2.8 m,装货宽度为2.4 m,请通过计算,判断这辆汽车能否顺利通过大门.
图3
16.如图5,在一面靠墙(墙足够长)的空地上,用长为24米的篱笆围成中间隔有两道篱笆的矩形花圃,设花圃的一边AB的长为x米,面积为S平方米.
(1)求S关于x的函数表达式及自变量x的取值范围;
(2)当x取何值时,所围成的花圃面积最大 最大面积是多少
图5
17.在美化校园的活动中,某兴趣小组想借助如图8所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x m.
(1)若花园的面积为192 m2,求x的值;
(2)若在点P处有一棵树与墙CD,AD的距离分别是15 m和6 m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园的最大面积.
图8
18. 小红经营的网店以销售文具为主,其中一款笔记本的进价为每本10元,该网店在试销售期间发现,该款笔记本每周的销售量y(本)与销售单价x(元/本)之间满足一次函数关系,三对对应值如下表:
销售单价x(元/本) 12 14 16
每周的销售量y(本) 500 400 300
(1)求y关于x的函数表达式(不要求写出自变量的取值范围);
(2)通过与其他网店对比,小红将这款笔记本的单价定为x元/本(12≤x≤15,且x为整数),设每周销售该款笔记本所获利润为w元,当销售单价定为多少时每周所获利润最大,最大利润是多少元
19 某超市销售一种品牌的牛奶,进价为每箱24元,规定售价不低于进价.当售价为每箱36元时,每月可销售60箱.经市场调查发现,这种品牌牛奶的售价每箱每降低1元,每月的销售量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销售量为y箱.
(1)写出y与x之间的函数表达式和自变量x的取值范围;
(2)超市如何定价,才能使每月销售牛奶获得的利润最大 最大利润是多少元
20 因疫情防控需要,消毒用品需求量增加.某药店新进一批桶装消毒液,每桶进价50元,每天的销售量y(桶)与销售单价x(元/桶)之间满足一次函数关系,其图象如图1-5-10所示.
(1)求y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)每桶消毒液的销售单价定为多少时,药店每天获得的利润最大,最大利润是多少元 (利润=销售价-进价)
图1-5-10
21 某服装批发市场销售一种衬衫,衬衫每件的进货价为50元.规定每件售价不低于进货价,经市场调查,每月的销售量y(件)与售价x(元/件)满足一次函数关系,部分数据如下表:
售价x(元/件) 60 65 70
销售量y(件) 1400 1300 1200
(1)求出y与x之间的函数表达式;(不需要求自变量x的取值范围)
(2)该批发市场每月想从这种衬衫销售中获利24000元,又想尽量给客户实惠,该如何给这种衬衫定价
(3)物价部门规定,该衬衫的每件利润不允许高于进货价的30%,设这种衬衫每月的总利润为w元,那么售价定为多少可获得最大利润 最大利润是多少
答案
1.C 2.B 3.A 4.B 5.B 6.A .7.C 8.B 9.B
10.2
11.14
12.5
13.3.75
14.35
15.解:(1)点A,B,C的坐标分别为A(-2,0),B(2,0),C(0,4.4).
设抛物线所表示的函数表达式为y=a(x-2)(x+2).
将点C(0,4.4)代入,得a×(0-2)×(0+2)=4.4,
解得a=-1.1,∴y=-1.1(x-2)(x+2)=-1.1x2+4.4.
即该抛物线所表示的函数表达式为y=-1.1x2+4.4.
(2)∵货物顶端距地面2.8 m,装货宽度为2.4 m,
∴只要判断点(-1.2,2.8)或点(1.2,2.8)与抛物线的位置关系即可.将x=1.2代入y=-1.1x2+4.4,得y=2.816>2.8,∴这辆汽车能顺利通过大门.
16.解:(1)∵AB=x米,∴BC=(24-4x)米,∴S=AB·BC=x(24-4x)=-4x2+24x(0(2)S=-4x2+24x=-4(x-3)2+36.∵0即当x取3时,所围成的花圃面积最大,最大面积是36平方米.
17.解:(1)∵AB=x m,∴BC=(28-x)m.根据题意,得x(28-x)=192,解得x1=12,x2=16,
即x的值为12或16.
(2)设花园的面积为S m2,则S=x(28-x)=-x2+28x=-(x-14)2+196.∵在点P处有一棵树与墙CD,AD的距离分别是15 m和6 m,∴解得6≤x≤13,此时S随x的增大而增大,
∴当x=13时,S最大值=-(13-14)2+196=195.答:花园的最大面积为195 m2.
18.解:(1)设y关于x的函数表达式是y=kx+b(k≠0),把x=12,y=500;x=14,y=400代入,得解得即y关于x的函数表达式为y=-50x+1100.
(2)由题意,可得w=(x-10)y=(x-10)(-50x+1100)=-50x2+1600x-11000=-50(x-16)2+1800.
∵a=-50<0,∴w有最大值,∴当x<16时,w随x的增大而增大.∵12≤x≤15,x为整数,
∴当x=15时,w有最大值,此时,w=-50×(15-16)2+1800=1750.
答:当销售单价定为15元/本时,每周所获利润最大,最大利润是1750元.
19.解:(1)根据题意,得y=60+10x.由36-x≥24,得x≤12,∴1≤x≤12,且x为整数.
(2)设所获利润为W元,则W=(36-x-24)(60+10x)=-10x2+60x+720=-10(x-3)2+810,
∴当x=3时,W取得最大值,最大值为810.此时售价为36-3=33(元/箱).
答:超市将牛奶的销售单价定为33元/箱时,才能使每月销售牛奶获得的利润最大,最大利润是810元.
20.解:(1)设y与x之间的函数表达式为y=kx+b.
将点(60,100),(70,80)代入y=kx+b中,得解得
故y与x之间的函数表达式为y=-2x+220.
(2)设药店每天获得的利润为w元,由题意,得
w=(x-50)(-2x+220)=-2x2+320x-11000=-2(x-80)2+1800.
∵-2<0,∴函数有最大值,
∴当x=80时,w有最大值,此时最大值是1800,
故每桶消毒液的销售单价定为80元/桶时,药店每天获得的利润最大,最大利润是1800元.
21.解:(1)设y与x之间的函数表达式为y=kx+b,把(60,1400),(65,1300)代入y=kx+b中,
得解得
即y与x之间的函数表达式是y=-20x+2600.
(2)由题意,得(x-50)(-20x+2600)=24000,解得x1=70,x2=110,
∴当售价为70元/件或110元/件时,该批发市场每月从这种衬衫销售中获利24000元.
又∵尽量给客户实惠,∴这种衬衫定价为70元/件.
(3)由题意,可得w=(x-50)(-20x+2600)=-20(x-90)2+32000.
∵该衬衫的每件利润不允许高于进货价的30%,每件售价不低于进货价,
∴50≤x,且(x-50)÷50≤30%,解得50≤x≤65.
∵当x<90时,w随x的增大而增大,
∴当x=65时,w取得最大值,此时w=19500.
答:当售价定为65元/件时可获得最大利润,最大利润是19500元.
一、选择题
1.河北省赵县赵州桥的桥拱是近似的抛物线形,建立如图1②所示的平面直角坐标系,其函数表达式为y=-x2.当水面离桥拱顶部的距离DO是4 m时,水面宽度AB为( )
图1
A.-20 m B.10 m C.20 m D.-10 m
2.小东在某次投篮中,球的运动线路是抛物线y=-x2+3.5的一部分(如图2),若命中篮圈中心,则他与篮底的距离l是( )
图2
A.3.5 m B.4 m C.4.5 m D.4.6 m
3.小敏用一根长为8 cm的细铁丝围成矩形,则矩形的最大面积是( )
A.4 cm2 B.8 cm2 C.16 cm2 D.32 cm2
4 如图6是抛物线形拱桥,当拱顶离水面2 m时,水面宽为4 m.当水面上升1.5 m时,水面的宽度为( )
图6
A.1 m B.2 m C. m D.2 m
5.某超市有一种商品,进价为每件2元,据市场调查发现,销售单价是13元/件时,平均每天的销售量是50件,而销售单价每降低1元,平均每天就可以多售出10件.若设销售单价降低x元,每天的利润为y元,则y与x之间的函数表达式为( )
A.y=(13-x)(50+10x) B.y=(11-x)(50+10x)
C.y=(2-x)(50+10x) D.y=(11-x)(50+x)
6.服装店将进价为100元/件的服装按x元/件出售,每天可销售(200-x)件.规定售价不低于进价.若想获得最大利润,则x的值为( )
A.150 B.160 C.170 D.180
7 竖直向上抛的物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=-5t2+v0t+h0表示,其中h0(m)是物体抛出时离地面的高度,v0(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5 m的高处以20 m/s的速度竖直向上抛出,小球达到的离地面的最大高度为( )
A.23.5 m B.22.5 m C.21.5 m D.20.5 m
8.广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠与喷头的水平距离x(米)的函数表达式是y=-x2+6x(0≤x≤4),那么水珠的高度达到最大时,水珠与喷头的水平距离是( )
A.1米 B.2米 C.5米 D.6米
9. 某商店销售某件商品所获得的利润y(元)与所卖的件数x之间的关系满足y=-x2+1000x-200000,则当0
填空题
10.如图4,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,点P以2 cm/s的速度从点A开始沿AB向点B运动,点Q以1 cm/s的速度从点B开始沿BC向点C运动,如果点P,Q分别从点A,B同时出发,当△PBQ的面积最大时,运动时间为 s.
图4
11.某农场拟建两间矩形饲养室,一面靠在足够长的墙体上,中间用一道围栏隔开,并在如图7所示的两处各留1 m宽的门,所有围栏的总长(不含门)为26 m,若要使得建成的饲养室面积最大,则利用墙体的长度为 m.
图7
12.已知商场某商品的进价为每件40元,现在的销售单价是60元/件,一周内可卖出300件.市场调查反映:售价每件每涨价1元,一周内要少卖出10件商品.设售价每件涨价x元,当x=
时,商场能在一周内获得最大利润.
13.加工爆米花时,爆开且不煳的粒数的百分比称为“可食用率”.在特定条件下,可食用率y与加工时间x(单位:min)满足函数表达式y=-0.2x2+1.5x-2,则最佳加工时间为
min.
14.某商场购进一批单价为20元/件的日用商品,如果以30元/件的价格出售,那么半月内可售出400件.根据销售经验,提高销售单价会导致销售量减少,即销售单价每提高1元,半月内销售量将减少20件.当销售单价是 元/件时,该商场才能在半月内获得最大利润.
三、计算题
15.某工厂的大门是一抛物线水泥建筑物,大门地面宽AB为4 m,顶部C离地面高为4.4 m,以AB所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图3所示.
(1)求该抛物线所表示的函数表达式;
(2)现有一辆载满货物的汽车欲通过大门,货物顶端距地面2.8 m,装货宽度为2.4 m,请通过计算,判断这辆汽车能否顺利通过大门.
图3
16.如图5,在一面靠墙(墙足够长)的空地上,用长为24米的篱笆围成中间隔有两道篱笆的矩形花圃,设花圃的一边AB的长为x米,面积为S平方米.
(1)求S关于x的函数表达式及自变量x的取值范围;
(2)当x取何值时,所围成的花圃面积最大 最大面积是多少
图5
17.在美化校园的活动中,某兴趣小组想借助如图8所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x m.
(1)若花园的面积为192 m2,求x的值;
(2)若在点P处有一棵树与墙CD,AD的距离分别是15 m和6 m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园的最大面积.
图8
18. 小红经营的网店以销售文具为主,其中一款笔记本的进价为每本10元,该网店在试销售期间发现,该款笔记本每周的销售量y(本)与销售单价x(元/本)之间满足一次函数关系,三对对应值如下表:
销售单价x(元/本) 12 14 16
每周的销售量y(本) 500 400 300
(1)求y关于x的函数表达式(不要求写出自变量的取值范围);
(2)通过与其他网店对比,小红将这款笔记本的单价定为x元/本(12≤x≤15,且x为整数),设每周销售该款笔记本所获利润为w元,当销售单价定为多少时每周所获利润最大,最大利润是多少元
19 某超市销售一种品牌的牛奶,进价为每箱24元,规定售价不低于进价.当售价为每箱36元时,每月可销售60箱.经市场调查发现,这种品牌牛奶的售价每箱每降低1元,每月的销售量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销售量为y箱.
(1)写出y与x之间的函数表达式和自变量x的取值范围;
(2)超市如何定价,才能使每月销售牛奶获得的利润最大 最大利润是多少元
20 因疫情防控需要,消毒用品需求量增加.某药店新进一批桶装消毒液,每桶进价50元,每天的销售量y(桶)与销售单价x(元/桶)之间满足一次函数关系,其图象如图1-5-10所示.
(1)求y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)每桶消毒液的销售单价定为多少时,药店每天获得的利润最大,最大利润是多少元 (利润=销售价-进价)
图1-5-10
21 某服装批发市场销售一种衬衫,衬衫每件的进货价为50元.规定每件售价不低于进货价,经市场调查,每月的销售量y(件)与售价x(元/件)满足一次函数关系,部分数据如下表:
售价x(元/件) 60 65 70
销售量y(件) 1400 1300 1200
(1)求出y与x之间的函数表达式;(不需要求自变量x的取值范围)
(2)该批发市场每月想从这种衬衫销售中获利24000元,又想尽量给客户实惠,该如何给这种衬衫定价
(3)物价部门规定,该衬衫的每件利润不允许高于进货价的30%,设这种衬衫每月的总利润为w元,那么售价定为多少可获得最大利润 最大利润是多少
答案
1.C 2.B 3.A 4.B 5.B 6.A .7.C 8.B 9.B
10.2
11.14
12.5
13.3.75
14.35
15.解:(1)点A,B,C的坐标分别为A(-2,0),B(2,0),C(0,4.4).
设抛物线所表示的函数表达式为y=a(x-2)(x+2).
将点C(0,4.4)代入,得a×(0-2)×(0+2)=4.4,
解得a=-1.1,∴y=-1.1(x-2)(x+2)=-1.1x2+4.4.
即该抛物线所表示的函数表达式为y=-1.1x2+4.4.
(2)∵货物顶端距地面2.8 m,装货宽度为2.4 m,
∴只要判断点(-1.2,2.8)或点(1.2,2.8)与抛物线的位置关系即可.将x=1.2代入y=-1.1x2+4.4,得y=2.816>2.8,∴这辆汽车能顺利通过大门.
16.解:(1)∵AB=x米,∴BC=(24-4x)米,∴S=AB·BC=x(24-4x)=-4x2+24x(0
17.解:(1)∵AB=x m,∴BC=(28-x)m.根据题意,得x(28-x)=192,解得x1=12,x2=16,
即x的值为12或16.
(2)设花园的面积为S m2,则S=x(28-x)=-x2+28x=-(x-14)2+196.∵在点P处有一棵树与墙CD,AD的距离分别是15 m和6 m,∴解得6≤x≤13,此时S随x的增大而增大,
∴当x=13时,S最大值=-(13-14)2+196=195.答:花园的最大面积为195 m2.
18.解:(1)设y关于x的函数表达式是y=kx+b(k≠0),把x=12,y=500;x=14,y=400代入,得解得即y关于x的函数表达式为y=-50x+1100.
(2)由题意,可得w=(x-10)y=(x-10)(-50x+1100)=-50x2+1600x-11000=-50(x-16)2+1800.
∵a=-50<0,∴w有最大值,∴当x<16时,w随x的增大而增大.∵12≤x≤15,x为整数,
∴当x=15时,w有最大值,此时,w=-50×(15-16)2+1800=1750.
答:当销售单价定为15元/本时,每周所获利润最大,最大利润是1750元.
19.解:(1)根据题意,得y=60+10x.由36-x≥24,得x≤12,∴1≤x≤12,且x为整数.
(2)设所获利润为W元,则W=(36-x-24)(60+10x)=-10x2+60x+720=-10(x-3)2+810,
∴当x=3时,W取得最大值,最大值为810.此时售价为36-3=33(元/箱).
答:超市将牛奶的销售单价定为33元/箱时,才能使每月销售牛奶获得的利润最大,最大利润是810元.
20.解:(1)设y与x之间的函数表达式为y=kx+b.
将点(60,100),(70,80)代入y=kx+b中,得解得
故y与x之间的函数表达式为y=-2x+220.
(2)设药店每天获得的利润为w元,由题意,得
w=(x-50)(-2x+220)=-2x2+320x-11000=-2(x-80)2+1800.
∵-2<0,∴函数有最大值,
∴当x=80时,w有最大值,此时最大值是1800,
故每桶消毒液的销售单价定为80元/桶时,药店每天获得的利润最大,最大利润是1800元.
21.解:(1)设y与x之间的函数表达式为y=kx+b,把(60,1400),(65,1300)代入y=kx+b中,
得解得
即y与x之间的函数表达式是y=-20x+2600.
(2)由题意,得(x-50)(-20x+2600)=24000,解得x1=70,x2=110,
∴当售价为70元/件或110元/件时,该批发市场每月从这种衬衫销售中获利24000元.
又∵尽量给客户实惠,∴这种衬衫定价为70元/件.
(3)由题意,可得w=(x-50)(-20x+2600)=-20(x-90)2+32000.
∵该衬衫的每件利润不允许高于进货价的30%,每件售价不低于进货价,
∴50≤x,且(x-50)÷50≤30%,解得50≤x≤65.
∵当x<90时,w随x的增大而增大,
∴当x=65时,w取得最大值,此时w=19500.
答:当售价定为65元/件时可获得最大利润,最大利润是19500元.
