2021-2022学年湘教版九年级数学下册第1章 二次函数 单元测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版九年级数学下册第1章 二次函数 单元测试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 205.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 00:00:00 | ||
图片预览

文档简介
第1章 二次函数
一、选择题(本大题共8小题,每小题4分,共32分)
1.二次函数y=x2+2x-4的图象的顶点坐标为( )
A.(1,5) B.(-1,5) C.(-1,-5) D.(1,-5)
2.将抛物线y=x2-6x+5向上平移2个单位,再向右平移1个单位后,得到的抛物线所表示的函数表达式是( )
A.y=(x-4)2-6 B.y=(x-1)2-3 C.y=(x-2)2-2 D.y=(x-4)2-2
3.在平面直角坐标系中,对于二次函数y=(x-2)2+1,下列说法中错误的是( )
A.y的最小值为1
B.图象的顶点坐标为(2,1),对称轴为直线x=2
C.当x<2时,y的值随x值的增大而增大,当x≥2时,y的值随x值的增大而减小
D.它的图象可以由y=x2的图象向右平移2个单位,再向上平移1个单位得到
4.若A(-2,y1),B(0,y2),C(-,y3)是二次函数y=ax2-2ax+1(a是常数,且a<0)图象上的三点,则y1,y2,y3之间的大小关系为( )
A.y1>y2>y3 B.y1>y3>y2 C.y2>y3>y1 D.y3>y1>y2
5.为搞好环保,某公司准备修建一个长方体污水处理池,池底矩形的周长为100 m,则池底的最大面积是( )
A.600 m2 B.625 m2 C.650 m2 D.675 m2
6.某同学在用列表描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格,那么当x=5时,y的值为( )
x … -1 0 1 2 3 …
y … 8 3 0 -1 0 …
A.8 B.6 C.4 D.3
7.在同一坐标系中,二次函数y=ax2+bx与一次函数y=bx-a的图象可能是( )
图1
8.图2是二次函数y=ax2+bx+c的图象,对于下列说法:①ac>0,②2a+b>0,③4ac④a+b+c<0,⑤当x>0时,y随x的增大而减小.其中正确的是( )
图2
A.①②③ B.①②④ C.②③④ D.③④⑤
二、填空题(本大题共8小题,每小题4分,共32分)
9.若二次函数y=ax2+bx的图象开口向下,则a 0(填“=”“>”或“<”).
10.若函数y=(m2-m)是二次函数,则m= .
11.二次函数y=-2x2-4x+5的最大值是 .
12.请写出一个函数表达式,使其图象的对称轴为y轴: .
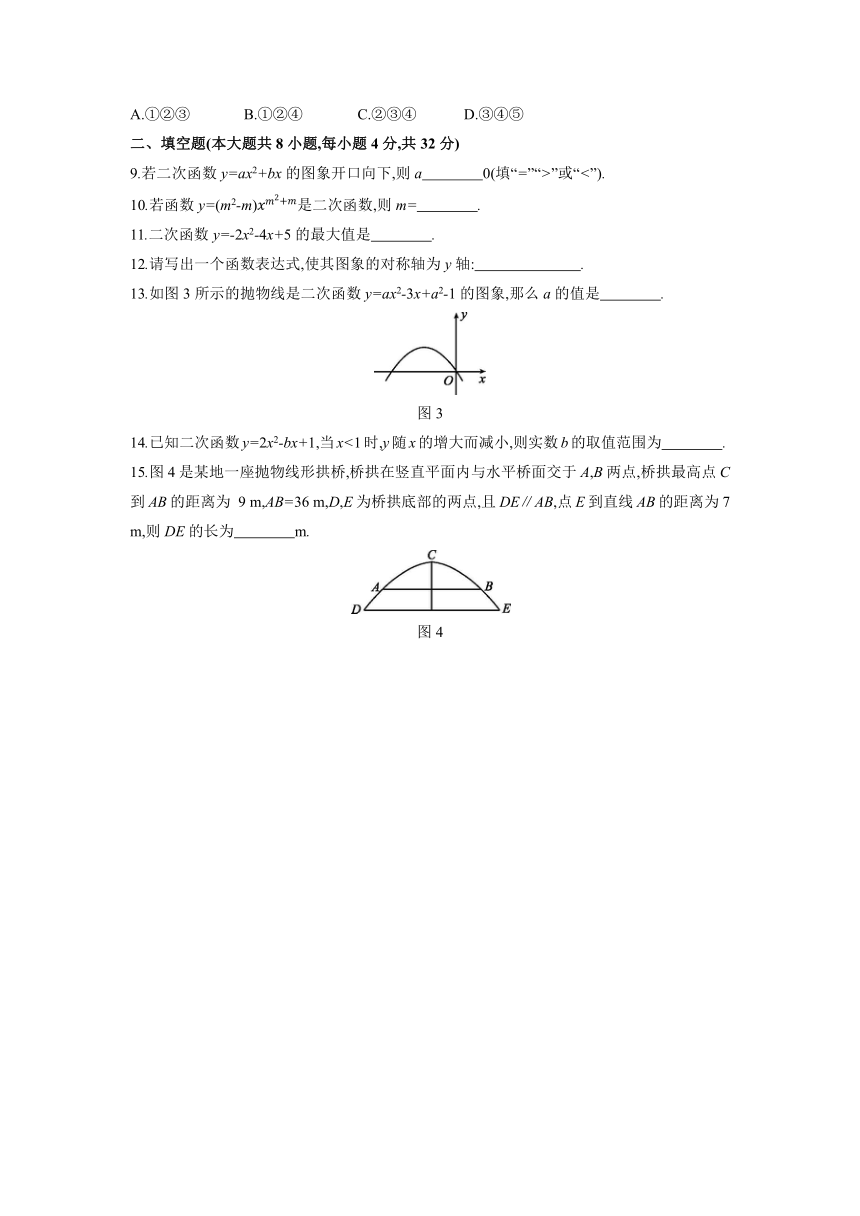
13.如图3所示的抛物线是二次函数y=ax2-3x+a2-1的图象,那么a的值是 .
图3
14.已知二次函数y=2x2-bx+1,当x<1时,y随x的增大而减小,则实数b的取值范围为 .
15.图4是某地一座抛物线形拱桥,桥拱在竖直平面内与水平桥面交于A,B两点,桥拱最高点C到AB的距离为 9 m,AB=36 m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为7 m,则DE的长为 m.
图4
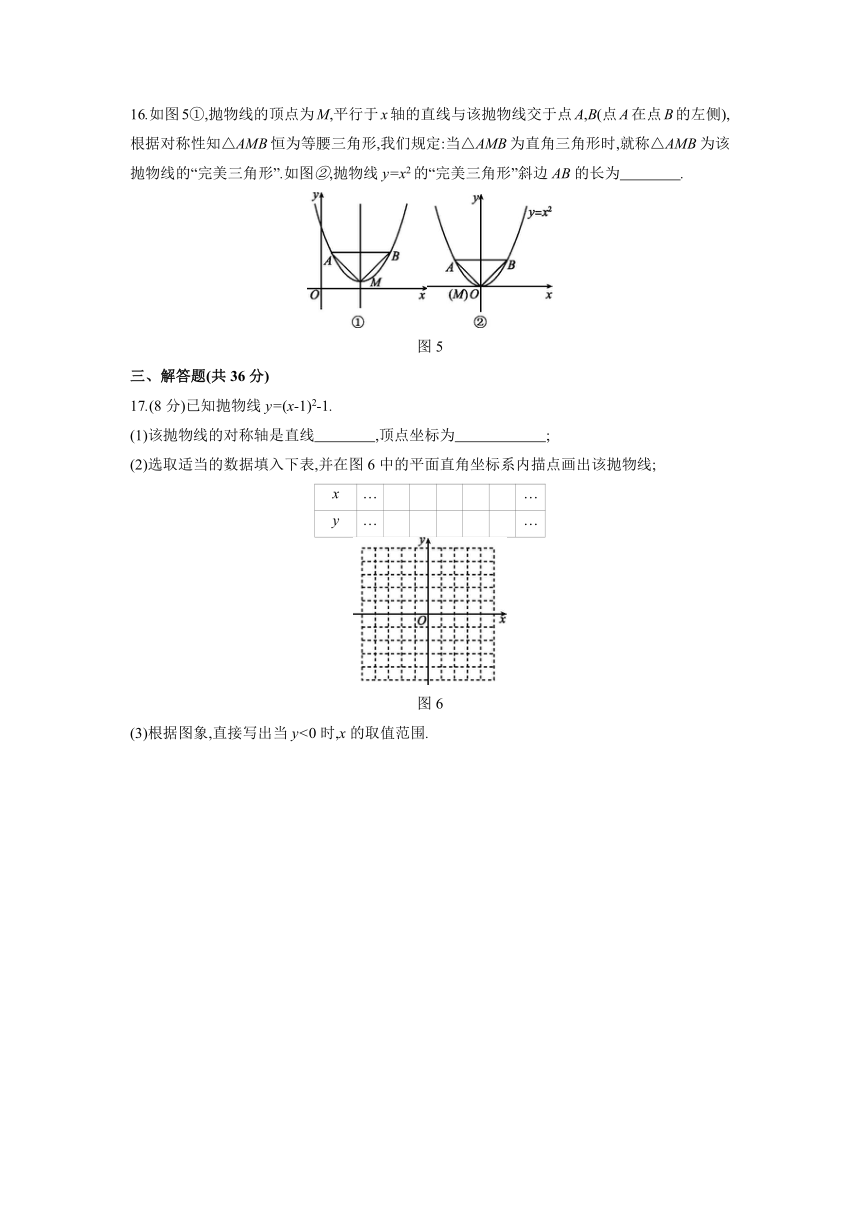
16.如图5①,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B的左侧),根据对称性知△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.如图②,抛物线y=x2的“完美三角形”斜边AB的长为 .
图5
三、解答题(共36分)
17.(8分)已知抛物线y=(x-1)2-1.
(1)该抛物线的对称轴是直线 ,顶点坐标为 ;
(2)选取适当的数据填入下表,并在图6中的平面直角坐标系内描点画出该抛物线;
x … …
y … …
图6
(3)根据图象,直接写出当y<0时,x的取值范围.
18.(8分)如图7,在平面直角坐标系中,二次函数y=ax2+4x-3图象的顶点是A,与x轴交于B,C两点,与y轴交于点D.点B的坐标是(1,0).
(1)求A,C两点的坐标,并根据图象直接写出当y>0时x的取值范围;
(2)平移该二次函数的图象,使点D恰好落在点A的位置上,求平移后图象所对应的二次函数的表达式.
图7
19.(10分)如图8,开口向下的抛物线与x轴交于点A(-1,0),B(2,0),与y轴交于点C(0,4),P是第一象限内抛物线上的一点.
(1)求该抛物线所表示的二次函数的表达式;
(2)设四边形CABP的面积为S,求S的最大值.
图8
20.(10分)图9是一座抛物线形拱桥,点P 处有一照明灯,水面OA 宽4 m.从O,A 两处观测点P 处,仰角分别为α,β,且tanα=,tanβ=.以点O 为原点,OA 所在直线为x 轴,建立平面直角坐标系.(1)求点P的坐标;
(2)若水面上升1 m,则水面宽为多少米(取1.41,结果精确到0.1 m)
图9
答案
C 2.D 3.C 4.C 5.B 6.A 7.C 8.C
9.<
10.-2 11.7
12.y=x2(答案不唯一) 13.-1
14.b≥4
15.48
16.2
17.解:(1)x=1 (1,-1)
(2)列表(也可选取其他的数据填表):
x … -1 0 1 2 3 …
y … 3 0 -1 0 3 …
图略.
(3)当y<0时,x的取值范围是018.解:(1)把B(1,0)代入y=ax2+4x-3,得0=a+4-3,解得a=-1,∴y=-x2+4x-3=-(x-2)2+1,
∴A(2,1).∵图象的对称轴为直线x=2,点B与点C关于直线x=2对称,∴C(3,0),
∴当y>0时,1(2)当x=0时,y=-x2+4x-3=-3,∴D(0,-3),∴点D平移到点A,抛物线向右平移2个单位,向上平移4个单位,可得平移后图象所对应的二次函数的表达式为y=-(x-4)2+5.
19.解:(1)∵A(-1,0),B(2,0),C(0,4),∴设抛物线所表示的二次函数的表达式为y=a(x+1)(x-2),
将点C(0,4)代入,得4=-2a,解得a=-2,
∴该抛物线所表示的二次函数的表达式为y=-2(x+1)(x-2)=-2x2+2x+4.
(2)如图,连接OP,设点P的坐标为(m,-2m2+2m+4),0∵A(-1,0),B(2,0),C(0,4),可得OA=1,OC=4,OB=2,∴S=S△OAC+S△OCP+S△OPB
=×1×4+×4m+×2×(-2m2+2m+4)=-2m2+4m+6
=-2(m-1)2+8,
∴当m=1时,S最大,最大值为8.
20.解:(1)如图,过点P 作PB⊥OA,垂足为B.设点P 的坐标为(x,y).
在Rt△POB 中,∵tanα==,∴OB==2y.在Rt△PAB 中,∵tanβ==,
∴AB==y.∵OA=OB+AB,即2y+y=4,∴y=,∴x=OB=2×=3,
∴点P 的坐标为3,.
(2)设这条抛物线表示的二次函数的表达式为y=ax2+bx,由函数图象经过(4,0),3,两点,
可得 解方程组,得
∴这条抛物线表示的二次函数的表达式为y=-x2+2x.当水面上升1 m 时,水面的纵坐标为1,
即-x2+2x=1,解得x1=2-,x2=2+,
∴x2-x1=2+-(2-)=2≈2.8(m).
答:若水面上升1 m,则水面宽约为2.8 m.
一、选择题(本大题共8小题,每小题4分,共32分)
1.二次函数y=x2+2x-4的图象的顶点坐标为( )
A.(1,5) B.(-1,5) C.(-1,-5) D.(1,-5)
2.将抛物线y=x2-6x+5向上平移2个单位,再向右平移1个单位后,得到的抛物线所表示的函数表达式是( )
A.y=(x-4)2-6 B.y=(x-1)2-3 C.y=(x-2)2-2 D.y=(x-4)2-2
3.在平面直角坐标系中,对于二次函数y=(x-2)2+1,下列说法中错误的是( )
A.y的最小值为1
B.图象的顶点坐标为(2,1),对称轴为直线x=2
C.当x<2时,y的值随x值的增大而增大,当x≥2时,y的值随x值的增大而减小
D.它的图象可以由y=x2的图象向右平移2个单位,再向上平移1个单位得到
4.若A(-2,y1),B(0,y2),C(-,y3)是二次函数y=ax2-2ax+1(a是常数,且a<0)图象上的三点,则y1,y2,y3之间的大小关系为( )
A.y1>y2>y3 B.y1>y3>y2 C.y2>y3>y1 D.y3>y1>y2
5.为搞好环保,某公司准备修建一个长方体污水处理池,池底矩形的周长为100 m,则池底的最大面积是( )
A.600 m2 B.625 m2 C.650 m2 D.675 m2
6.某同学在用列表描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格,那么当x=5时,y的值为( )
x … -1 0 1 2 3 …
y … 8 3 0 -1 0 …
A.8 B.6 C.4 D.3
7.在同一坐标系中,二次函数y=ax2+bx与一次函数y=bx-a的图象可能是( )
图1
8.图2是二次函数y=ax2+bx+c的图象,对于下列说法:①ac>0,②2a+b>0,③4ac
图2
A.①②③ B.①②④ C.②③④ D.③④⑤
二、填空题(本大题共8小题,每小题4分,共32分)
9.若二次函数y=ax2+bx的图象开口向下,则a 0(填“=”“>”或“<”).
10.若函数y=(m2-m)是二次函数,则m= .
11.二次函数y=-2x2-4x+5的最大值是 .
12.请写出一个函数表达式,使其图象的对称轴为y轴: .
13.如图3所示的抛物线是二次函数y=ax2-3x+a2-1的图象,那么a的值是 .
图3
14.已知二次函数y=2x2-bx+1,当x<1时,y随x的增大而减小,则实数b的取值范围为 .
15.图4是某地一座抛物线形拱桥,桥拱在竖直平面内与水平桥面交于A,B两点,桥拱最高点C到AB的距离为 9 m,AB=36 m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为7 m,则DE的长为 m.
图4
16.如图5①,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B的左侧),根据对称性知△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.如图②,抛物线y=x2的“完美三角形”斜边AB的长为 .
图5
三、解答题(共36分)
17.(8分)已知抛物线y=(x-1)2-1.
(1)该抛物线的对称轴是直线 ,顶点坐标为 ;
(2)选取适当的数据填入下表,并在图6中的平面直角坐标系内描点画出该抛物线;
x … …
y … …
图6
(3)根据图象,直接写出当y<0时,x的取值范围.
18.(8分)如图7,在平面直角坐标系中,二次函数y=ax2+4x-3图象的顶点是A,与x轴交于B,C两点,与y轴交于点D.点B的坐标是(1,0).
(1)求A,C两点的坐标,并根据图象直接写出当y>0时x的取值范围;
(2)平移该二次函数的图象,使点D恰好落在点A的位置上,求平移后图象所对应的二次函数的表达式.
图7
19.(10分)如图8,开口向下的抛物线与x轴交于点A(-1,0),B(2,0),与y轴交于点C(0,4),P是第一象限内抛物线上的一点.
(1)求该抛物线所表示的二次函数的表达式;
(2)设四边形CABP的面积为S,求S的最大值.
图8
20.(10分)图9是一座抛物线形拱桥,点P 处有一照明灯,水面OA 宽4 m.从O,A 两处观测点P 处,仰角分别为α,β,且tanα=,tanβ=.以点O 为原点,OA 所在直线为x 轴,建立平面直角坐标系.(1)求点P的坐标;
(2)若水面上升1 m,则水面宽为多少米(取1.41,结果精确到0.1 m)
图9
答案
C 2.D 3.C 4.C 5.B 6.A 7.C 8.C
9.<
10.-2 11.7
12.y=x2(答案不唯一) 13.-1
14.b≥4
15.48
16.2
17.解:(1)x=1 (1,-1)
(2)列表(也可选取其他的数据填表):
x … -1 0 1 2 3 …
y … 3 0 -1 0 3 …
图略.
(3)当y<0时,x的取值范围是0
∴A(2,1).∵图象的对称轴为直线x=2,点B与点C关于直线x=2对称,∴C(3,0),
∴当y>0时,1
19.解:(1)∵A(-1,0),B(2,0),C(0,4),∴设抛物线所表示的二次函数的表达式为y=a(x+1)(x-2),
将点C(0,4)代入,得4=-2a,解得a=-2,
∴该抛物线所表示的二次函数的表达式为y=-2(x+1)(x-2)=-2x2+2x+4.
(2)如图,连接OP,设点P的坐标为(m,-2m2+2m+4),0
=×1×4+×4m+×2×(-2m2+2m+4)=-2m2+4m+6
=-2(m-1)2+8,
∴当m=1时,S最大,最大值为8.
20.解:(1)如图,过点P 作PB⊥OA,垂足为B.设点P 的坐标为(x,y).
在Rt△POB 中,∵tanα==,∴OB==2y.在Rt△PAB 中,∵tanβ==,
∴AB==y.∵OA=OB+AB,即2y+y=4,∴y=,∴x=OB=2×=3,
∴点P 的坐标为3,.
(2)设这条抛物线表示的二次函数的表达式为y=ax2+bx,由函数图象经过(4,0),3,两点,
可得 解方程组,得
∴这条抛物线表示的二次函数的表达式为y=-x2+2x.当水面上升1 m 时,水面的纵坐标为1,
即-x2+2x=1,解得x1=2-,x2=2+,
∴x2-x1=2+-(2-)=2≈2.8(m).
答:若水面上升1 m,则水面宽约为2.8 m.
