苏科版八年级上册第六章一次函数复习 复习课件(17张ppt)
文档属性
| 名称 | 苏科版八年级上册第六章一次函数复习 复习课件(17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 13:04:57 | ||
图片预览






文档简介
(共17张PPT)
一 次 函 数 复 习
一、知识要点:
2.一次函数的概念:函数y=_______(k、b为常数, k______)叫做一次函数;当b_____时,函数y=____(k____)叫做正比例函数.
kx +b
≠0
= 0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴解析式中自变量x的次数是___次,⑵比例系数_____。
1
k≠0
3.正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________.
4.一次函数y=kx+b(k≠0)的图象是过点(0,___), (____,0)的__________.
0,0
1,k
一条直线
b
一条直线
1.什么是常量?什么是变量?什么是函数?
4.正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____.
⑵当k<0时,图象过______象限;y随x的增大而____.
一、三
增大
二、四
减小
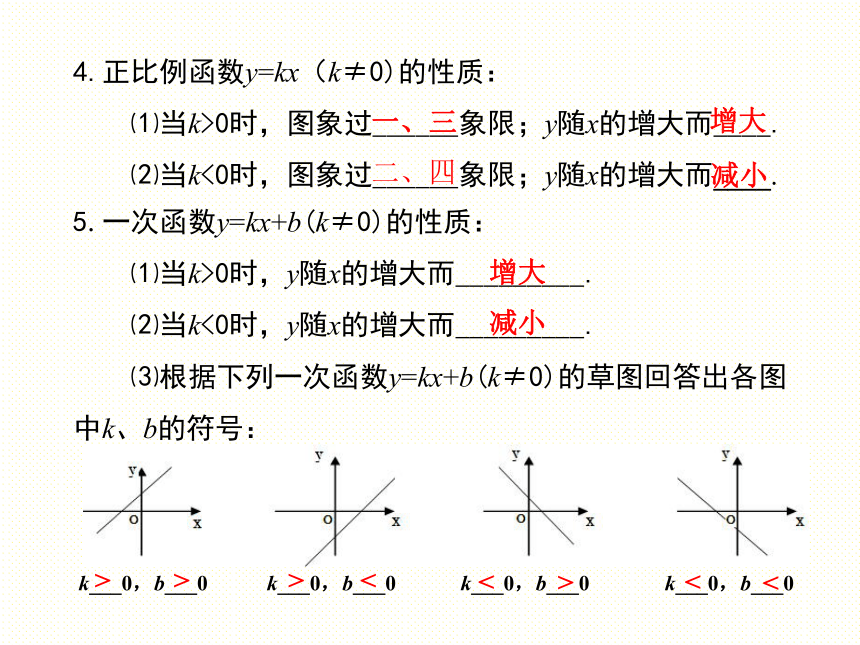
5.一次函数y=kx+b(k≠0)的性质:
⑴当k>0时,y随x的增大而_________.
⑵当k<0时,y随x的增大而_________.
⑶根据下列一次函数y=kx+b(k≠0)的草图回答出各图
中k、b的符号:
增大
减小
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
<
<
>
<
<
>
>
>
②
①、②、③
④
③
(2)如果一次函数y=kx-3k+6的图象经过原点,那么k的值为________.
(3)已知y-1与x成正比例,且x=-2时,y=4,那么y与x之间的函数关系式为_________________.
k=2
例1 填空:
(1)有下列函数:① ②
③ ④ 其中过原点的直线是_____;函数y随x的增大而增大的是___________;函数y随x的增大而减小的是______;图象在第一、二、三象限的是_____.
二、例题选讲:
例2 已知点A(x1 , y1)、B(x2 , y2)在一次函数y=kx+b(k<0,b<0)的图像上,且x1 < x2,则y1与y2的大小关系是_____________.
y1 > y2
二、例题选讲:
例3、如图表示一个正比例函数与一个一次函数的
图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.
x
y
B
O
A
二、例题选讲:
(1)直线OA:
(2)直线AB:
例3、已知直线y=3x与y=-x+4,求:
(1)这两条直线的交点;
(2)这两条直线与y轴围成的三角形面积.
二、例题选讲:
(1)两直线交点坐标为(1,3)
(2)两直线与y轴交点坐标为(0,0),(0,4)
∴围成的三角形面积为2.
1.已知函数
(1)若y是x的一次函数,则n= .
(2)若y是x的正比例函数,则m+n= .
2.已知y与x成正比例,如果当x=4时,y=2,那么x=3时,y=( )
A.1.5 B.2 C.3 D.6
-1
-4
A
三、自主练习:
5.已知一次函数的图象经过点A(2,-1)
和点B,B是另一直线y=-0.5x+3与y轴的交点,这个一次函数的解析式___________.
3.函数y=2x-1与x轴交点坐标为_______ ,与y轴交点坐标为__ __,与两坐标轴围成的三角形面积是______.
(0.5 ,0)
(0,-1)
4.若直线y=kx+b和直线y=-x平行,与y轴交点的纵坐标为-2,则直线的解析式为___________.
0.25
6.已知(y-3)与x成正比例
(1)求证:y是x的一次函数。
(2)当x=2时,y=-1,求y与x的函数关系式.
解:(1)设y-3=kx,则y=kx+3,所以y是x的一次函数.
(2)把x=2,y=-1代入y=kx+3,得-1=2k+3,解得k=-2,所以y=-2x+3 .
7.拖拉机开始工作时,油箱中有油40升。如果每小时耗油5升,求油箱中余油量Q(L)与工作时间t(h)之间的函数关系式,写出自变量t的取值范围并画出图像.
解:根据题意可得Q=-5t+40.当Q=0时解得t=8(h),所以0≤t≤8(h).图像如图
t(h)
Q(L)
o
10
20
30
40
1
2
3
4
5
特别提醒:实际问题的图像一定要考虑自变量的取值范围
8.已知:点P是一次函数y=-2x+8的图象上一点,如果图象与x轴交于Q点,且△OPQ的面积等于8,求P点的坐标.
x
y
o
y=-2x+8
Q
P
解:在函数y=-2x+8中,当y=0时,x=4,所以OQ=4,又因为S△OPQ= ,所
以8= ,解得h=4,
即点P的纵坐标y=4或-4,
代入解析式可得x=2或6.
∴点P的坐标为(2,4)或(6,-4).
9.已知直线y=ax+2分别与x轴和y轴交于
B、C两点,直线y=-2x+b与x轴交于点A,
并且两直线交点P为(2,4)
(1)求两直线表达式;
(2)求四边形AOCP的面积.
x
y
O
A
B
P(2,4)
C
(1)直线BC: y=x+2,
直线AP:y=-2x+8;
(2)S四边形A0CP=S△APB-S△BOC=12-2=10
10.已知直线y= kx+b 与x轴正半轴交于A, 与y轴负半轴交于B.若直线经过点(-1,-4),且OA+OB=3,求它的函数表达式.
x
y
o
A
B
直线的函数表达式是: y=2x-2
分析 先用k,b表示A、B两点坐标,通过列方程来解.用坐标表示OA、OB的长度时,要注意坐标的符号.
11. 快车和慢车分别从甲、乙两地同时出发,匀速相向而行,快车到达乙地后,慢车继续前行,设出发x小时后,两车相距y千米,图中折线表示从两车出发至慢车到达甲地的过程中y与x之间的函数关系式,根据图中信息,解答下列问题.
(1)甲、乙两地相距 千米,快车从甲地到乙地所用的时间是 小时;
(2)求线段PQ的函数解析式(写出自变量取值范围),并说明点Q的实际意义.
(3)求快车和慢车的速度.
640
(2)设线段PQ的解析式为y =kx+640,
将(1.25 ,440)代入,
得 1.25k+640=440,∴ k =-160,
∴线段PQ的解析式为y =-160x+640 ,
当y =0时,-160x+640=0,解得x=4,
故点Q的坐标为(4,0),故Q的实际意义为出发4小时后两车相遇;
6.4
(3)快车的速度:640÷6.4=100(千米/时),
两车的速度和:640÷4=160(千米/时),
∴慢车的速度为:160-100=60(千米/时).
答:快车的速度为100千米/时,慢车的速度为60千米/时.
12.甲、乙两车同时从A地出发驶向B地.甲车到达B地后立即返回,设甲车离A地的距离为y1(km),乙车离A地的距离为y2 (km),行驶时间为x(h), y1 ,y2与x的函数关系如图所示.
(1)填空:A、B两地相距 千米,甲车从B地返回A地的行驶速度是 千米/时;
(2)当两车行驶7小时后在途中相遇,求点E的坐标;
(3)甲车从B地返回A地途中,与乙车相距100千米时,求甲车行驶的时间.
(2)设直线CD的解析式为 y1 =kx+b,
把(6,800)和(14,0)代入可得k=-100,b=1400,
则直线CD的解析式为 y1 =-100x+1400,
当x=7时,y=700,
则点E的坐标为(7,700);
(3)设直线OF的解析式为 y2=hx,
把点E的坐标(7,700)代入得,h=100,
则直线OF的解析式为 y2=100x,
当y1- y2=100时,-100x+1400-100x=100,解得: x=6.5;
当y2-y1 =100时,100x-(-100x+1400)=100,解得,x=7.5,
答:甲车行驶的时间为 6.5小时或7.5小时.
800
100
一 次 函 数 复 习
一、知识要点:
2.一次函数的概念:函数y=_______(k、b为常数, k______)叫做一次函数;当b_____时,函数y=____(k____)叫做正比例函数.
kx +b
≠0
= 0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴解析式中自变量x的次数是___次,⑵比例系数_____。
1
k≠0
3.正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________.
4.一次函数y=kx+b(k≠0)的图象是过点(0,___), (____,0)的__________.
0,0
1,k
一条直线
b
一条直线
1.什么是常量?什么是变量?什么是函数?
4.正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____.
⑵当k<0时,图象过______象限;y随x的增大而____.
一、三
增大
二、四
减小
5.一次函数y=kx+b(k≠0)的性质:
⑴当k>0时,y随x的增大而_________.
⑵当k<0时,y随x的增大而_________.
⑶根据下列一次函数y=kx+b(k≠0)的草图回答出各图
中k、b的符号:
增大
减小
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
<
<
>
<
<
>
>
>
②
①、②、③
④
③
(2)如果一次函数y=kx-3k+6的图象经过原点,那么k的值为________.
(3)已知y-1与x成正比例,且x=-2时,y=4,那么y与x之间的函数关系式为_________________.
k=2
例1 填空:
(1)有下列函数:① ②
③ ④ 其中过原点的直线是_____;函数y随x的增大而增大的是___________;函数y随x的增大而减小的是______;图象在第一、二、三象限的是_____.
二、例题选讲:
例2 已知点A(x1 , y1)、B(x2 , y2)在一次函数y=kx+b(k<0,b<0)的图像上,且x1 < x2,则y1与y2的大小关系是_____________.
y1 > y2
二、例题选讲:
例3、如图表示一个正比例函数与一个一次函数的
图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.
x
y
B
O
A
二、例题选讲:
(1)直线OA:
(2)直线AB:
例3、已知直线y=3x与y=-x+4,求:
(1)这两条直线的交点;
(2)这两条直线与y轴围成的三角形面积.
二、例题选讲:
(1)两直线交点坐标为(1,3)
(2)两直线与y轴交点坐标为(0,0),(0,4)
∴围成的三角形面积为2.
1.已知函数
(1)若y是x的一次函数,则n= .
(2)若y是x的正比例函数,则m+n= .
2.已知y与x成正比例,如果当x=4时,y=2,那么x=3时,y=( )
A.1.5 B.2 C.3 D.6
-1
-4
A
三、自主练习:
5.已知一次函数的图象经过点A(2,-1)
和点B,B是另一直线y=-0.5x+3与y轴的交点,这个一次函数的解析式___________.
3.函数y=2x-1与x轴交点坐标为_______ ,与y轴交点坐标为__ __,与两坐标轴围成的三角形面积是______.
(0.5 ,0)
(0,-1)
4.若直线y=kx+b和直线y=-x平行,与y轴交点的纵坐标为-2,则直线的解析式为___________.
0.25
6.已知(y-3)与x成正比例
(1)求证:y是x的一次函数。
(2)当x=2时,y=-1,求y与x的函数关系式.
解:(1)设y-3=kx,则y=kx+3,所以y是x的一次函数.
(2)把x=2,y=-1代入y=kx+3,得-1=2k+3,解得k=-2,所以y=-2x+3 .
7.拖拉机开始工作时,油箱中有油40升。如果每小时耗油5升,求油箱中余油量Q(L)与工作时间t(h)之间的函数关系式,写出自变量t的取值范围并画出图像.
解:根据题意可得Q=-5t+40.当Q=0时解得t=8(h),所以0≤t≤8(h).图像如图
t(h)
Q(L)
o
10
20
30
40
1
2
3
4
5
特别提醒:实际问题的图像一定要考虑自变量的取值范围
8.已知:点P是一次函数y=-2x+8的图象上一点,如果图象与x轴交于Q点,且△OPQ的面积等于8,求P点的坐标.
x
y
o
y=-2x+8
Q
P
解:在函数y=-2x+8中,当y=0时,x=4,所以OQ=4,又因为S△OPQ= ,所
以8= ,解得h=4,
即点P的纵坐标y=4或-4,
代入解析式可得x=2或6.
∴点P的坐标为(2,4)或(6,-4).
9.已知直线y=ax+2分别与x轴和y轴交于
B、C两点,直线y=-2x+b与x轴交于点A,
并且两直线交点P为(2,4)
(1)求两直线表达式;
(2)求四边形AOCP的面积.
x
y
O
A
B
P(2,4)
C
(1)直线BC: y=x+2,
直线AP:y=-2x+8;
(2)S四边形A0CP=S△APB-S△BOC=12-2=10
10.已知直线y= kx+b 与x轴正半轴交于A, 与y轴负半轴交于B.若直线经过点(-1,-4),且OA+OB=3,求它的函数表达式.
x
y
o
A
B
直线的函数表达式是: y=2x-2
分析 先用k,b表示A、B两点坐标,通过列方程来解.用坐标表示OA、OB的长度时,要注意坐标的符号.
11. 快车和慢车分别从甲、乙两地同时出发,匀速相向而行,快车到达乙地后,慢车继续前行,设出发x小时后,两车相距y千米,图中折线表示从两车出发至慢车到达甲地的过程中y与x之间的函数关系式,根据图中信息,解答下列问题.
(1)甲、乙两地相距 千米,快车从甲地到乙地所用的时间是 小时;
(2)求线段PQ的函数解析式(写出自变量取值范围),并说明点Q的实际意义.
(3)求快车和慢车的速度.
640
(2)设线段PQ的解析式为y =kx+640,
将(1.25 ,440)代入,
得 1.25k+640=440,∴ k =-160,
∴线段PQ的解析式为y =-160x+640 ,
当y =0时,-160x+640=0,解得x=4,
故点Q的坐标为(4,0),故Q的实际意义为出发4小时后两车相遇;
6.4
(3)快车的速度:640÷6.4=100(千米/时),
两车的速度和:640÷4=160(千米/时),
∴慢车的速度为:160-100=60(千米/时).
答:快车的速度为100千米/时,慢车的速度为60千米/时.
12.甲、乙两车同时从A地出发驶向B地.甲车到达B地后立即返回,设甲车离A地的距离为y1(km),乙车离A地的距离为y2 (km),行驶时间为x(h), y1 ,y2与x的函数关系如图所示.
(1)填空:A、B两地相距 千米,甲车从B地返回A地的行驶速度是 千米/时;
(2)当两车行驶7小时后在途中相遇,求点E的坐标;
(3)甲车从B地返回A地途中,与乙车相距100千米时,求甲车行驶的时间.
(2)设直线CD的解析式为 y1 =kx+b,
把(6,800)和(14,0)代入可得k=-100,b=1400,
则直线CD的解析式为 y1 =-100x+1400,
当x=7时,y=700,
则点E的坐标为(7,700);
(3)设直线OF的解析式为 y2=hx,
把点E的坐标(7,700)代入得,h=100,
则直线OF的解析式为 y2=100x,
当y1- y2=100时,-100x+1400-100x=100,解得: x=6.5;
当y2-y1 =100时,100x-(-100x+1400)=100,解得,x=7.5,
答:甲车行驶的时间为 6.5小时或7.5小时.
800
100
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
