高中数学人教A版(2019)必修 第一册 3.2.1.1 函数的基本性质-函数的单调性 课件(共32张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)必修 第一册 3.2.1.1 函数的基本性质-函数的单调性 课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
3.2 函数的基本性质
3.2.1 单调性与最大(小)值
第1课时 函数的单调性
【情境探究】
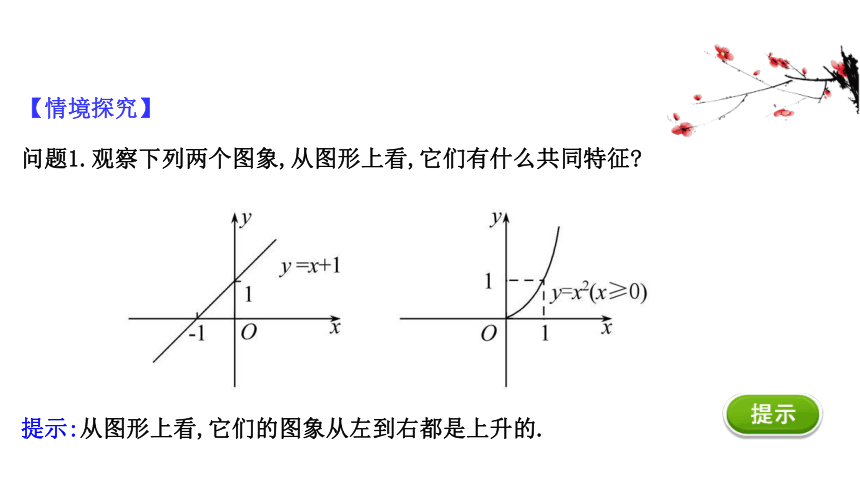
问题1.观察下列两个图象,从图形上看,它们有什么共同特征
必备知识生成
提示:从图形上看,它们的图象从左到右都是上升的.
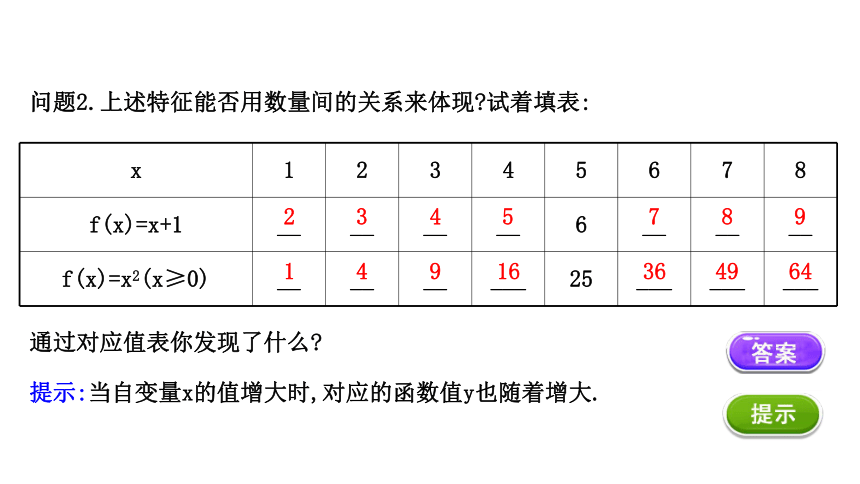
问题2.上述特征能否用数量间的关系来体现 试着填表:
x 1 2 3 4 5 6 7 8
f(x)=x+1 __ __ __ __ 6 __ __ __
f(x)=x2(x≥0) __ __ __ ___ 25 ___ ___ ___
通过对应值表你发现了什么
提示:当自变量x的值增大时,对应的函数值y也随着增大.
2
3
4
5
7
8
9
1
4
9
16
36
49
64
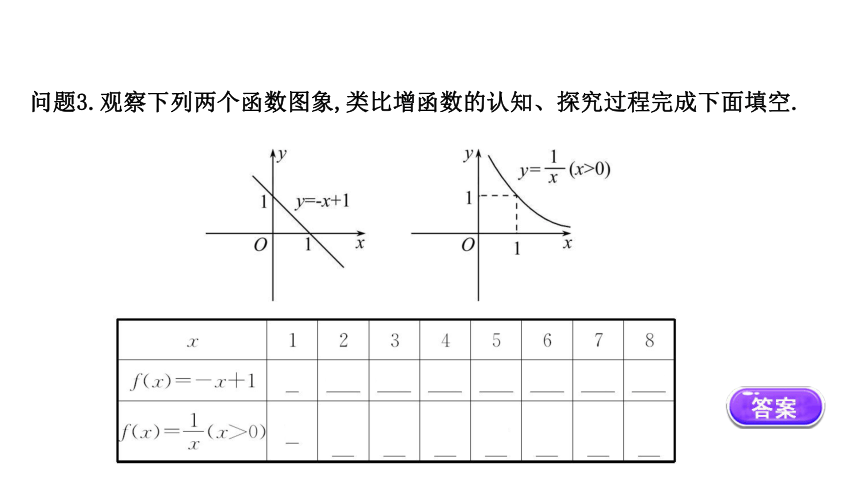
问题3.观察下列两个函数图象,类比增函数的认知、探究过程完成下面填空.
通过对应值表及图象观察你发现了什么
提示:当自变量x的值增大时, 对应的函数值y逐渐减小.
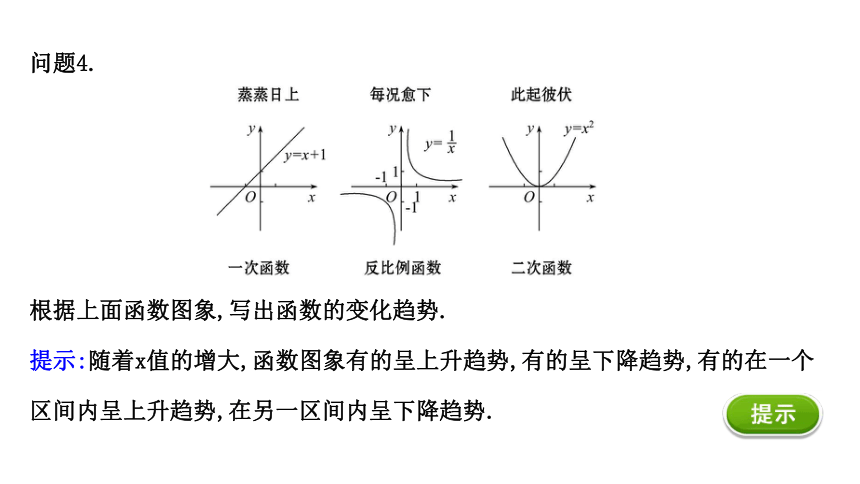
问题4.
根据上面函数图象,写出函数的变化趋势.
提示:随着x值的增大,函数图象有的呈上升趋势,有的呈下降趋势,有的在一个区间内呈上升趋势,在另一区间内呈下降趋势.
【知识生成】
1.增函数的定义
一般地,设函数f(x)的定义域为I,区间D I;
如果 x1,x2∈D,当x1单调递增.
特别地,当函数f(x)在它的定义域上单调递增时,我们就称它是增函数.
f(x1)2.减函数的定义
如果 x1,x2∈D,当x1单调递减.
特别地,当函数f(x)在它的定义域上单调递减时,我们就称它是减函数.
3.单调性定义
如果函数y=f(x)在区间D上___________________,那么就说函数y=f(x)
在这一区间具有(严格的)单调性.区间D叫做y=f(x)的_________.
f(x1)>f(x2)
单调递增或单调递减
单调区间
关键能力探究
探究点一 依据函数图象求单调区间
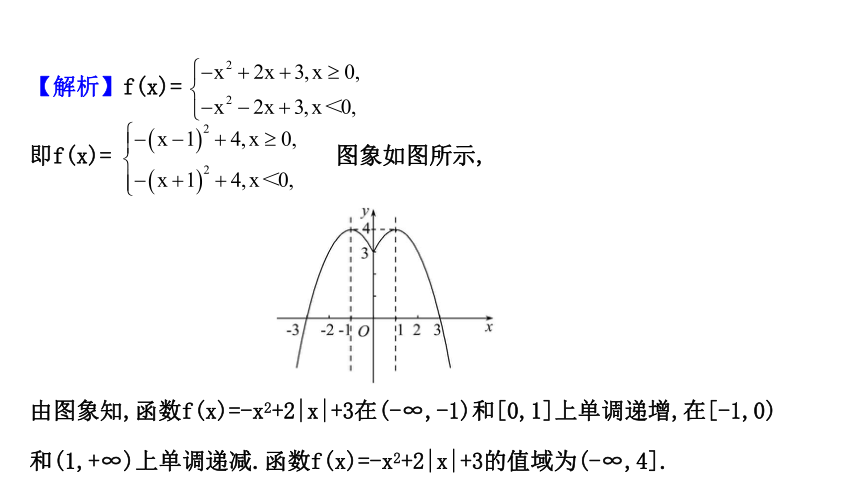
【典例1】求函数f(x)=-x2+2|x|+3的单调区间,并指出其值域.
【思维导引】作出函数f(x)=-x2+2|x|+3的图象,根据图象观察得到.
【解析】f(x)=
即f(x)= 图象如图所示,
由图象知,函数f(x)=-x2+2|x|+3在(-∞,-1)和[0,1]上单调递增,在[-1,0)
和(1,+∞)上单调递减.函数f(x)=-x2+2|x|+3的值域为(-∞,4].
【类题通法】求函数单调区间的三种方法
方法一:将函数转化为已知的基本初等函数(如一次函数、二次函数等)再进行单调性的判断.
方法二:定义法.即先求出定义域,再利用单调性的定义进行判断求解.
方法三:图象法.即先画出图象,根据图象求单调区间.
提醒:一个函数出现两个或两个以上的单调区间时,不能用“∪”而应该用“和”或“,”来表示.
【定向训练】
1.求下列函数的单调区间,并指出其在单调区间上的单调性.
(1)y=3x-2.(2)y=- .(3)y=-x2+2x+3.
【解析】(1)函数y=3x-2的单调区间为R,其在R上是增函数.
(2)函数y=- 的单调区间为(-∞,0),(0,+∞),其在(-∞,0)及(0,+∞)上
单调递增.
(3)函数y=-x2+2x+3的对称轴为x=1,并且开口向下,其单调增区间为(-∞,1],
单调减区间为(1,+∞),其在(-∞,1]上单调递增,在(1,+∞)上单调递减.
2.作出函数f(x)= 的图象,并指出函数的单调区间.
【解析】f(x)= 的图象如图所示.
由图可知,函数的单调减区间为(-∞,1]和(1,2);
单调增区间为[2,+∞).
探究点二 函数单调性的判定与证明
【典例2】证明函数f(x)=x+ 在(2,+∞)上单调递增.
【思维导引】按证明区间上单调性的方法步骤套格式.
【证明】 x1,x2∈(2,+∞),且x1=(x1-x2)+
因为24,x1x2-4>0,所以f(x1)-f(x2)<0,
即f(x1)所以函数f(x)=x+ 在(2,+∞)上单调递增.
【互动探究】
(变问法)若本例的函数不变,试判断f(x)在(0,2)上的单调性.
【解析】函数f(x)=x+ 在(0,2)上单调递减.理由如下:
x1,x2∈(0,2),且x1=(x1-x2)+
因为0所以f(x1)-f(x2)>0,即f(x1)>f(x2).
所以函数f(x)=x+ 在(0,2)上单调递减.
【类题通法】利用定义证明函数单调性的步骤
注意:作差变形是证明函数单调性的关键,且变形的方向是因式乘积的形式.
【定向训练】
1.下列四个函数在(-∞,0)上单调递增的是 ( )
①y=|x|+1;②y= ;③y= ;④y=x+
A.①② B.②③ C.③④ D.①④
【解析】选C.①y=|x|+1=-x+1(x<0)在(-∞,0)上单调递减;②y= =-1(x<0)
在(-∞,0)上既不单调递增,也不单调递减;③y=- =x(x<0)在(-∞,0)上
单调递增;④y=x+ =x-1(x<0)在(-∞,0)上单调递增.
2.已知函数f(x)= ,证明:函数f(x)在(-1,+∞)上单调递减.
【证明】 x1,x2∈(-1,+∞),且x1则f(x1)-f(x2)=
因为x2>x1>-1,所以x2-x1>0,(x1+1)(x2+1)>0,
因此f(x1)-f(x2)>0,即f(x1)>f(x2),
所以f(x)在(-1,+∞)上单调递减.
探究点三 函数单调性的应用
【典例3】若函数y= 在(-1,+∞)上单调递增,求a的取值范围.
【思维导引】将y= 化为y=a- ,再由增减性确定a的范围.
【解析】因为y=
在(-1,+∞)上单调递增,所以a>0,即a的取值范围是a>0.
【延伸探究】
1.若加上条件“y= -(a-2)x在(-1,+∞)上单调递增”,求a的取值范围.
【解析】由函数y= -(a-2)x在(-1,+∞)上单调递增得:a-2<0,即a<2.
又因为y= 在(-1,+∞)上单调递增,所以a>0,综上,02.若条件改为f(x)= 在R上为增函数,求a的取值范围.
【解析】由y= -(a-2)x在(-∞,1]上递增,
得a-2<0,即a<2.
由y= 在(1,+∞)上递增,得a>0,
又f(x)在R上为增函数,所以还需 -(a-2)×1≤ ,得a≥
综上,a的取值范围是 ≤a<2.
【类题通法】函数单调性应用的两个关注点
(1)单调性的定义的“双向性”:利用定义可以判断、证明函数的单调性,反过来,若已知函数的单调性可以确定函数中参数的取值范围.
(2)若一个函数在区间[a,b]上是单调的,则此函数在这一单调区间内的任意子集上也是单调的.
【定向训练】
1.函数y= 在(-1,+∞)上单调递增,则a的取值范围是 ( )
A.a=-3 B.a<3 C.a≤-3 D.a≥-3
【解析】选C.y=
需
即 所以a≤-3.
2.已知函数f(x)=-x2-2(a+1)x+3.
(1)函数f(x)在区间(-∞,3]上单调递增,则实数a的取值范围是________.
(2)函数f(x)的单调递增区间是(-∞,3],则实数a的值为________.
【解析】y=-x2-2(a+1)x+3=-(x+a+1)2+(a+1)2+3.
所以该函数的单调递增区间为(-∞,-a-1].
(1)因为函数y=-x2-2(a+1)x+3在区间(-∞,3]上单调递增,所以3≤-a-1,
即a≤-4.
(2)由题意得-a-1=3,a=-4.
答案:(1)(-∞,-4] (2)-4
【补偿训练】已知函数f(x)=kx2-4x-8在区间[2,10]上具有单调性,则实数k的取值范围为________.
【解析】当k=0时,满足题意.
当k≠0时,f(x)=
因为f(x)在[2,10]上有单调性,所以 ≥10或 ≤2,
所以0综上,k≥1或k≤ .
答案:k≥1或k≤
函数的
单调性
核心知识
方法总结
易错提醒
核心素养
当c>0时,函数f(x)与cf(x)的单调性相同;
当c<0时,函数f(x)与cf(x)的单调性相反,
函数f(x)和g(x)单调性相同,则f(x)+g(x)的单调性与其相同
函数f(x)与f(x)+c的单调性相同;
单调递增
单调区间
单调递减
图象
单调性的判断
(1)单调区间必须是函数定义域的子集
(2)若函数f(x)在其定义城内的两个区间A.B上都是增函数(或减函数)。一般不能简单认为
f(x)在A∪B上是增函数
(3)函数单调区间的书写若在区间端点处有定义,则写成开区间或闭区间都可
数学抽象:通过具体函数图象抽象出定义,培养数学抽象的核心素养
逻辑推理:通过具体函数单调性的证明,培养逻辑推理的核心素养
课堂素养达标
1.函数f(x)的图象如图所示,则 ( )
A.函数f(x)在[-1,2]上单调递增
B.函数f(x)在[-1,2]上单调递减
C.函数f(x)在[-1,4]上单调递减
D.函数f(x)在[2,4]上单调递增
【解析】选A.结合题干图象可知函数f(x)在[-1,2]上是“上升”的,故A正确.
2.函数y=-x2+2x-2的单调递减区间是 ( )
A.(-∞,1] B.[1,+∞)
C.(-∞,2] D.[2,+∞)
【解析】选B.因为函数y=-x2+2x-2的开口向下,且对称轴为x=1,所以函数
y=-x2+2x-2的单调递减区间是[1,+∞).
3.若函数y=- 在(0,+∞)上单调递减,则实数b的取值范围是________.
【解析】由反比例函数的单调性知,-b>0,所以b<0.
答案:(-∞,0)
4.若f(x)在R上是单调递减的,且f(x-2)【解析】由题意可得,x-2>3,解得x>5.
答案:(5,+∞)
5.如图分别为函数y=f(x)和y=g(x)的图象,试写出函数y=f(x)和y=g(x)的单调增区间.
【解析】由题图(1)可知,在[1,4)和[4,6)上,y=f(x)是单调递增的.
由题图(2)可知,在[-4.5,0)和(4.5,7.5]上,y=g(x)是单调递增的.
3.2 函数的基本性质
3.2.1 单调性与最大(小)值
第1课时 函数的单调性
【情境探究】
问题1.观察下列两个图象,从图形上看,它们有什么共同特征
必备知识生成
提示:从图形上看,它们的图象从左到右都是上升的.
问题2.上述特征能否用数量间的关系来体现 试着填表:
x 1 2 3 4 5 6 7 8
f(x)=x+1 __ __ __ __ 6 __ __ __
f(x)=x2(x≥0) __ __ __ ___ 25 ___ ___ ___
通过对应值表你发现了什么
提示:当自变量x的值增大时,对应的函数值y也随着增大.
2
3
4
5
7
8
9
1
4
9
16
36
49
64
问题3.观察下列两个函数图象,类比增函数的认知、探究过程完成下面填空.
通过对应值表及图象观察你发现了什么
提示:当自变量x的值增大时, 对应的函数值y逐渐减小.
问题4.
根据上面函数图象,写出函数的变化趋势.
提示:随着x值的增大,函数图象有的呈上升趋势,有的呈下降趋势,有的在一个区间内呈上升趋势,在另一区间内呈下降趋势.
【知识生成】
1.增函数的定义
一般地,设函数f(x)的定义域为I,区间D I;
如果 x1,x2∈D,当x1
特别地,当函数f(x)在它的定义域上单调递增时,我们就称它是增函数.
f(x1)
如果 x1,x2∈D,当x1
特别地,当函数f(x)在它的定义域上单调递减时,我们就称它是减函数.
3.单调性定义
如果函数y=f(x)在区间D上___________________,那么就说函数y=f(x)
在这一区间具有(严格的)单调性.区间D叫做y=f(x)的_________.
f(x1)>f(x2)
单调递增或单调递减
单调区间
关键能力探究
探究点一 依据函数图象求单调区间
【典例1】求函数f(x)=-x2+2|x|+3的单调区间,并指出其值域.
【思维导引】作出函数f(x)=-x2+2|x|+3的图象,根据图象观察得到.
【解析】f(x)=
即f(x)= 图象如图所示,
由图象知,函数f(x)=-x2+2|x|+3在(-∞,-1)和[0,1]上单调递增,在[-1,0)
和(1,+∞)上单调递减.函数f(x)=-x2+2|x|+3的值域为(-∞,4].
【类题通法】求函数单调区间的三种方法
方法一:将函数转化为已知的基本初等函数(如一次函数、二次函数等)再进行单调性的判断.
方法二:定义法.即先求出定义域,再利用单调性的定义进行判断求解.
方法三:图象法.即先画出图象,根据图象求单调区间.
提醒:一个函数出现两个或两个以上的单调区间时,不能用“∪”而应该用“和”或“,”来表示.
【定向训练】
1.求下列函数的单调区间,并指出其在单调区间上的单调性.
(1)y=3x-2.(2)y=- .(3)y=-x2+2x+3.
【解析】(1)函数y=3x-2的单调区间为R,其在R上是增函数.
(2)函数y=- 的单调区间为(-∞,0),(0,+∞),其在(-∞,0)及(0,+∞)上
单调递增.
(3)函数y=-x2+2x+3的对称轴为x=1,并且开口向下,其单调增区间为(-∞,1],
单调减区间为(1,+∞),其在(-∞,1]上单调递增,在(1,+∞)上单调递减.
2.作出函数f(x)= 的图象,并指出函数的单调区间.
【解析】f(x)= 的图象如图所示.
由图可知,函数的单调减区间为(-∞,1]和(1,2);
单调增区间为[2,+∞).
探究点二 函数单调性的判定与证明
【典例2】证明函数f(x)=x+ 在(2,+∞)上单调递增.
【思维导引】按证明区间上单调性的方法步骤套格式.
【证明】 x1,x2∈(2,+∞),且x1
因为2
即f(x1)
【互动探究】
(变问法)若本例的函数不变,试判断f(x)在(0,2)上的单调性.
【解析】函数f(x)=x+ 在(0,2)上单调递减.理由如下:
x1,x2∈(0,2),且x1
因为0
所以函数f(x)=x+ 在(0,2)上单调递减.
【类题通法】利用定义证明函数单调性的步骤
注意:作差变形是证明函数单调性的关键,且变形的方向是因式乘积的形式.
【定向训练】
1.下列四个函数在(-∞,0)上单调递增的是 ( )
①y=|x|+1;②y= ;③y= ;④y=x+
A.①② B.②③ C.③④ D.①④
【解析】选C.①y=|x|+1=-x+1(x<0)在(-∞,0)上单调递减;②y= =-1(x<0)
在(-∞,0)上既不单调递增,也不单调递减;③y=- =x(x<0)在(-∞,0)上
单调递增;④y=x+ =x-1(x<0)在(-∞,0)上单调递增.
2.已知函数f(x)= ,证明:函数f(x)在(-1,+∞)上单调递减.
【证明】 x1,x2∈(-1,+∞),且x1
因为x2>x1>-1,所以x2-x1>0,(x1+1)(x2+1)>0,
因此f(x1)-f(x2)>0,即f(x1)>f(x2),
所以f(x)在(-1,+∞)上单调递减.
探究点三 函数单调性的应用
【典例3】若函数y= 在(-1,+∞)上单调递增,求a的取值范围.
【思维导引】将y= 化为y=a- ,再由增减性确定a的范围.
【解析】因为y=
在(-1,+∞)上单调递增,所以a>0,即a的取值范围是a>0.
【延伸探究】
1.若加上条件“y= -(a-2)x在(-1,+∞)上单调递增”,求a的取值范围.
【解析】由函数y= -(a-2)x在(-1,+∞)上单调递增得:a-2<0,即a<2.
又因为y= 在(-1,+∞)上单调递增,所以a>0,综上,0
【解析】由y= -(a-2)x在(-∞,1]上递增,
得a-2<0,即a<2.
由y= 在(1,+∞)上递增,得a>0,
又f(x)在R上为增函数,所以还需 -(a-2)×1≤ ,得a≥
综上,a的取值范围是 ≤a<2.
【类题通法】函数单调性应用的两个关注点
(1)单调性的定义的“双向性”:利用定义可以判断、证明函数的单调性,反过来,若已知函数的单调性可以确定函数中参数的取值范围.
(2)若一个函数在区间[a,b]上是单调的,则此函数在这一单调区间内的任意子集上也是单调的.
【定向训练】
1.函数y= 在(-1,+∞)上单调递增,则a的取值范围是 ( )
A.a=-3 B.a<3 C.a≤-3 D.a≥-3
【解析】选C.y=
需
即 所以a≤-3.
2.已知函数f(x)=-x2-2(a+1)x+3.
(1)函数f(x)在区间(-∞,3]上单调递增,则实数a的取值范围是________.
(2)函数f(x)的单调递增区间是(-∞,3],则实数a的值为________.
【解析】y=-x2-2(a+1)x+3=-(x+a+1)2+(a+1)2+3.
所以该函数的单调递增区间为(-∞,-a-1].
(1)因为函数y=-x2-2(a+1)x+3在区间(-∞,3]上单调递增,所以3≤-a-1,
即a≤-4.
(2)由题意得-a-1=3,a=-4.
答案:(1)(-∞,-4] (2)-4
【补偿训练】已知函数f(x)=kx2-4x-8在区间[2,10]上具有单调性,则实数k的取值范围为________.
【解析】当k=0时,满足题意.
当k≠0时,f(x)=
因为f(x)在[2,10]上有单调性,所以 ≥10或 ≤2,
所以0
答案:k≥1或k≤
函数的
单调性
核心知识
方法总结
易错提醒
核心素养
当c>0时,函数f(x)与cf(x)的单调性相同;
当c<0时,函数f(x)与cf(x)的单调性相反,
函数f(x)和g(x)单调性相同,则f(x)+g(x)的单调性与其相同
函数f(x)与f(x)+c的单调性相同;
单调递增
单调区间
单调递减
图象
单调性的判断
(1)单调区间必须是函数定义域的子集
(2)若函数f(x)在其定义城内的两个区间A.B上都是增函数(或减函数)。一般不能简单认为
f(x)在A∪B上是增函数
(3)函数单调区间的书写若在区间端点处有定义,则写成开区间或闭区间都可
数学抽象:通过具体函数图象抽象出定义,培养数学抽象的核心素养
逻辑推理:通过具体函数单调性的证明,培养逻辑推理的核心素养
课堂素养达标
1.函数f(x)的图象如图所示,则 ( )
A.函数f(x)在[-1,2]上单调递增
B.函数f(x)在[-1,2]上单调递减
C.函数f(x)在[-1,4]上单调递减
D.函数f(x)在[2,4]上单调递增
【解析】选A.结合题干图象可知函数f(x)在[-1,2]上是“上升”的,故A正确.
2.函数y=-x2+2x-2的单调递减区间是 ( )
A.(-∞,1] B.[1,+∞)
C.(-∞,2] D.[2,+∞)
【解析】选B.因为函数y=-x2+2x-2的开口向下,且对称轴为x=1,所以函数
y=-x2+2x-2的单调递减区间是[1,+∞).
3.若函数y=- 在(0,+∞)上单调递减,则实数b的取值范围是________.
【解析】由反比例函数的单调性知,-b>0,所以b<0.
答案:(-∞,0)
4.若f(x)在R上是单调递减的,且f(x-2)
答案:(5,+∞)
5.如图分别为函数y=f(x)和y=g(x)的图象,试写出函数y=f(x)和y=g(x)的单调增区间.
【解析】由题图(1)可知,在[1,4)和[4,6)上,y=f(x)是单调递增的.
由题图(2)可知,在[-4.5,0)和(4.5,7.5]上,y=g(x)是单调递增的.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
