课件--函数的单调性

课件25张PPT。§1.3.1 函数的单调性（新课标A版）观察下列函数的图象：答案 函数的单调性[m，n]上，函数
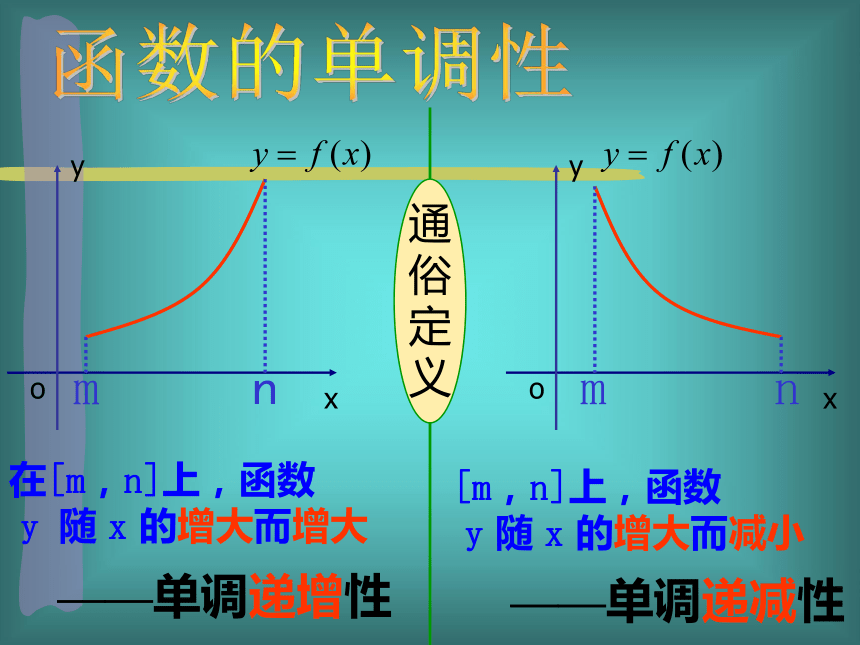
y 随 x 的增大而减小在[m，n]上，函数
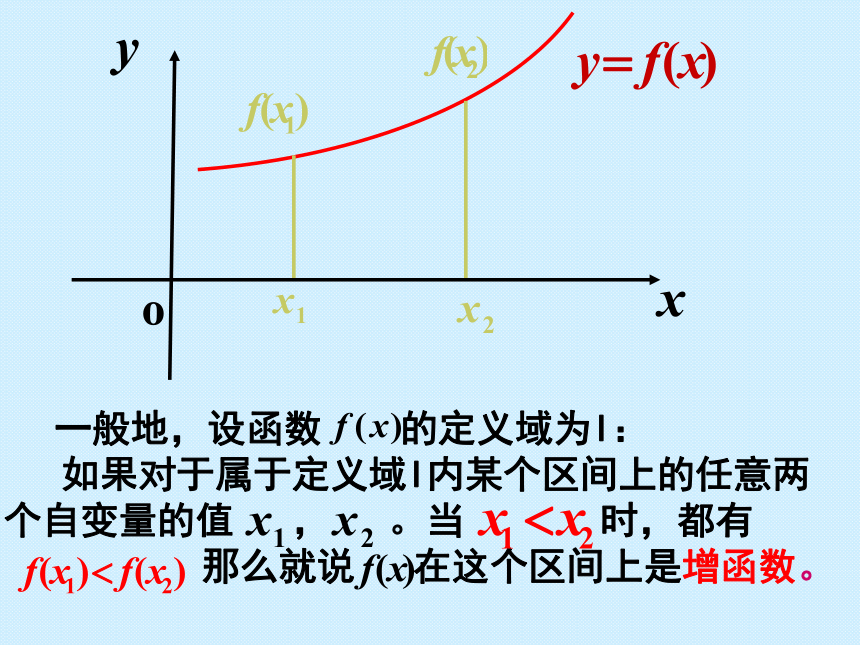
y 随 x 的增大而增大——单调递增性——单调递减性 一般地，设函数 的定义域为I：
如果对于属于定义域I内某个区间上的任意两个自变量的值 ， 。当 时，都有
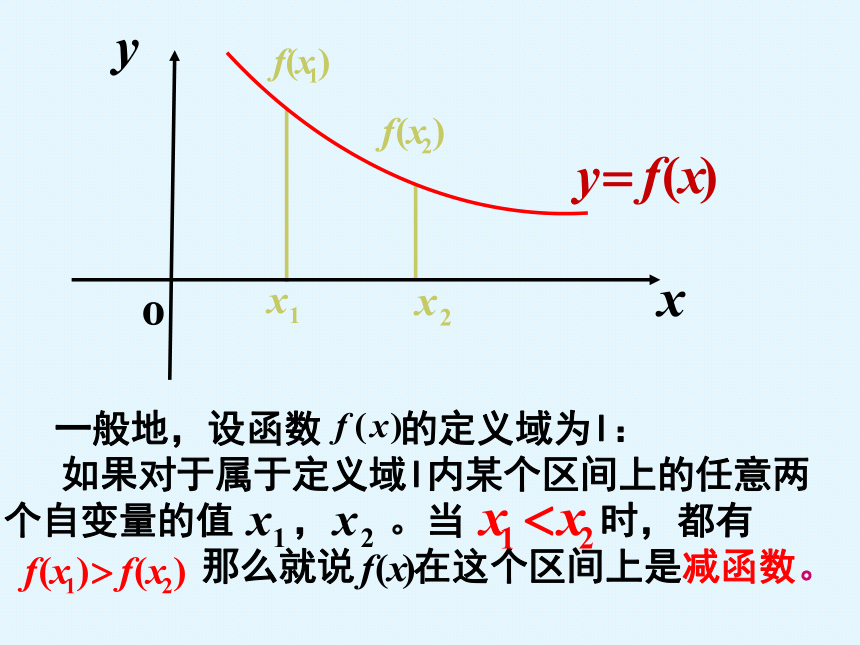
那么就说 在这个区间上是增函数。 一般地，设函数 的定义域为I：
如果对于属于定义域I内某个区间上的任意两个自变量的值 ， 。当 时，都有
那么就说 在这个区间上是减函数。我们开始接触到的函数中，那些是增函数，那些是减函数？？增函数：y=x+1 在R上是增函数。
y=- 在（-∞，0）和（0，+∞）是增函数。
y= 在（-∞，0）是增函数。
y= 在R上是增函数。减函数：y=-x+1 在R上是减函数。
y= 在（-∞，0）和（0，+∞）是减函数。
y= 在（ 0 ， +∞ ）是增函数。1.函数的单调性也就是
函数的增减性2.函数的单调性是对某个区间而言
的,它是一个局部概念.
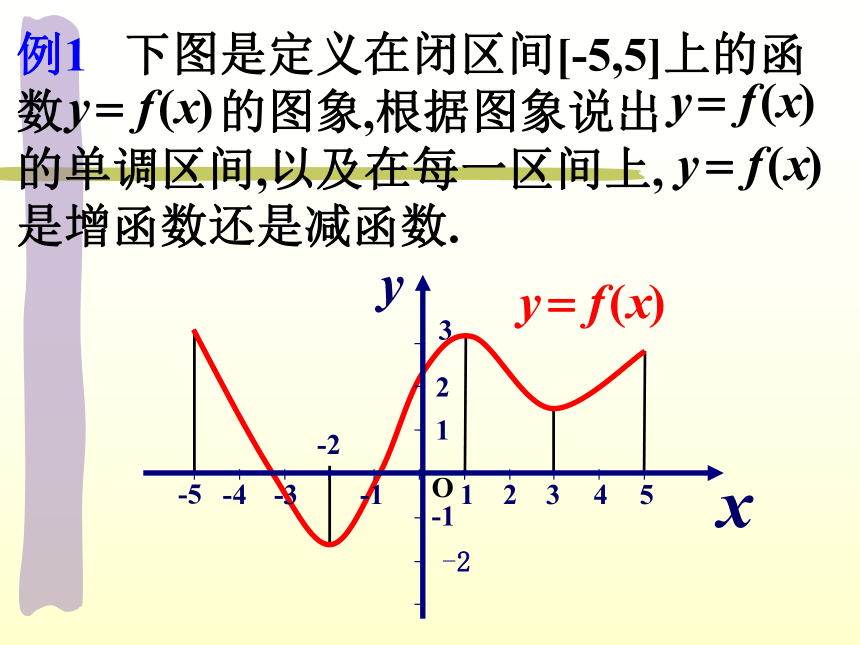
注：例1 下图是定义在闭区间[-5,5]上的函
数 的图象,根据图象说出
的单调区间,以及在每一区间上,
是增函数还是减函数.在区间[-5,-2), [1,3)上是减函数
在区间[-2,1), [3,5)上是增函数.解:函数 的单调区间有
[-5,-2), [-2,1), [1,3), [3,5],O如图,已知 的图象(包括端点),
根据图象说出函数的单调区间,以及
在每一区间上,函数是增函数还是减
函数.如图,已知 的图象(包括端点),
根据图象说出函数的单调区间,以及
在每一区间上,函数是增函数还是减
函数.-11o例2 证明函数 在R上是
增函数.判定函数在某个区间上的单调性的
方法步骤:3.判断上述差的符号 ;4.下结论(若差<0,则为增函数;
若差>0,则为减函数).1.设 给定的区间,且 ; 2.计算 至最简 ;例2 证明函数 在R上是增函数.证明：设 是R上的任意两个实数，且则于是即证明函数 在R上是减函数.证明：设 是R上的任意两个实数，且于是即则 证明函数 在R上是
减函数.试一试!例3 证明函数 在(0,+∞)上
是减函数.证明：设 是（0，+∞）上的任意两个
实数，且 ，则 于是 ，即所以， 在（0，+∞)上是减函数.
例3 证明函数 在(-∞,0)上
是减函数.证明：设 是（0，+∞）上的任意两个
实数，且 ，则 于是 ，即所以， 在（0，+∞)上是减函数.
例3 证明函数 在(-∞,0)上
是减函数. 由 ，得又由 ， 得于是 ，即所以， 在 上是减函数.
证明：设 是 上的任意两个
实数，且 ，则 (- ∞ ，0)(- ∞ ，0 ) 判断函数 在(0, +∞)上
是增函数还是减函数?并证明.试一试！ 证明函数 在(0, +∞)上是增函数. 证明：设 是(0, +∞)上的任意两个实数，且在(0, +∞)上是增函数.小结
１．讨论函数的单调性必须在定义域内进行，即函数的单调区间是其定义域的子集．因此讨论函数的单调性，必须先确定函数的定义域；
２．根据定义证明函数单调性的一般步骤是：
(1)设x1，x2是给定区间内的两个值,且x1(2)作差f(x1)－f(x2)；并将此差式变形(要注意变形的程度)；
(3)判断f(x1)－f(x2)的正负(要注意说理的充分性)；
(4)据据f(x1)－f(x2)的符号确定其增减性．思考:结合图象说出函数
的单调区间,以及在各个区间上是
增函数还是减函数;你能给出相应
的证明吗?再见