人教版九年级下册第二十七章相似图形经典例题讲解(51张ppt)
文档属性
| 名称 | 人教版九年级下册第二十七章相似图形经典例题讲解(51张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 788.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 18:50:43 | ||
图片预览










文档简介
(共51张PPT)
相似图形经典例题
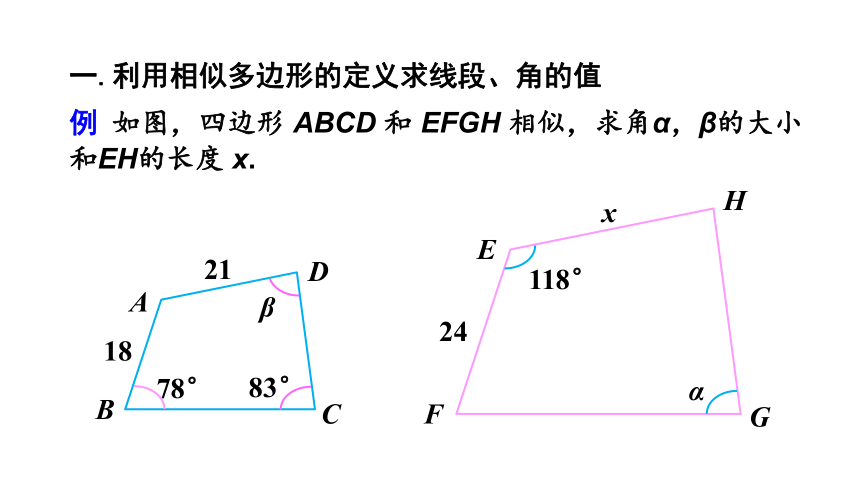
例 如图,四边形 ABCD 和 EFGH 相似,求角α,β的大小和EH的长度 x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
一.利用相似多边形的定义求线段、角的值
在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°.
解:∵ 四边形 ABCD 和 EFGH 相似,
∴ 它们的对应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
∵ 四边形ABCD和EFGH相似,
∴它们的对应边成比例,由此可得
解得 x = 28 .
,即 .
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
如图所示的两个五边形相似,求未知边a、b、c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
解:相似多边形的对应边的比相等,由此可得
, , , ,
解得:a=3,b=4.5,c=4,d=6.
所以未知边a,b,c,d的长度分别为3,4.5,4,6.
如图,把矩形 ABCD 对折,折痕为 EF,若矩形ABCD 与矩形 EABF 相似,AB = 1.
A
B
C
D
E
F
解:∵ E 是 AD 的中点,
∴ .
又∵矩形 ABCD 与矩形 EABF相似,AB=1,
∴ ,
∴ AB2 = AE·BC,
∴ .
解得
(1)求BC长;
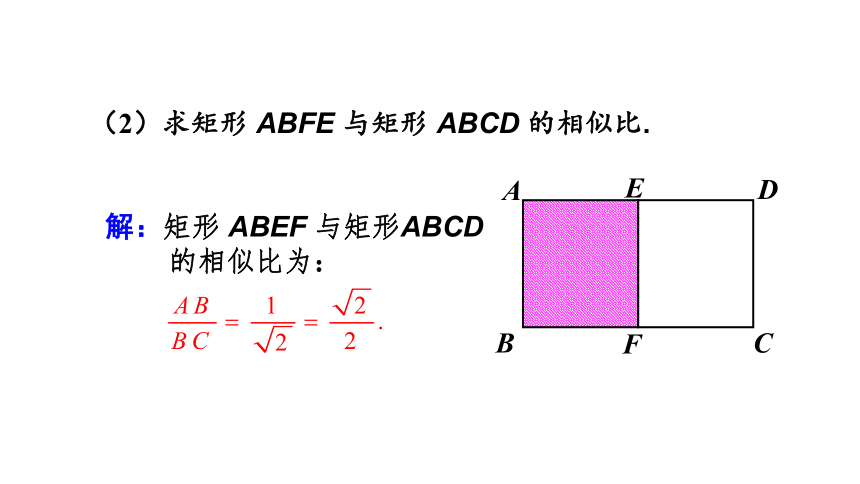
(2)求矩形 ABFE 与矩形 ABCD 的相似比.
A
B
C
D
E
F
解:矩形 ABEF 与矩形ABCD
的相似比为:
如图,l1∥l2∥l3, ,DE=6,求DF的长.
解:∵l1∥l2∥l3,
∴ .
又∵ ,DE=6,
∴ ,
解得EF=4.
∴DF=DE+EF=6+4=10.
l1
l2
l3
例 如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD.
∴AE=3.
解:∵AC=4,EC=1,
∵ DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
二.利用平行线分线段成比例定理及推论求线段长度
A
B
C
D
E
证明:在△ADE与△ABC中,
∠A= ∠A.
∵ DE//BC,
∴∠ADE=∠B, ∠AED=∠C,
过E作EF//AB交BC于F,
∵四边形DBFE是平行四边形,
F
∴DE=BF .
∴△ADE∽△ABC .
∴ .
∴ .
则
已知:如图,在△ABC中,DE//BC,且DE分别交AB , AC于点D、E.
求证:△ADE∽△ABC .
如图,在△ABC中, EF∥BC.
( 1 )如果E、F分别是 AB 和 AC 上的点, AE = BE=7,
FC = 4 ,那么 AF 的长是多少?
A
B
C
E
F
解:∵
∴
解得 AF = 4.
(2) 如果AB = 10,AE=6,AF = 5,那么 FC 的长是多少?
解:∵
∴
解得 .
A
B
C
E
F
如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.
求证:OD∶OA=OE∶OB
证明: ∵ DF∥AC,
∵ EF∥BC,
如图,已知菱形 ABCD 内接于△AEF,AE=5cm, AF = 4 cm,求菱形的边长.
解:∵ 四边形 ABCD 为菱形,
B
C
A
D
E
F
∴CD∥AB,
∴
设菱形的边长为 x cm,则CD
= AD = x cm,DF = (4-x )cm,
∴ 解得 ∴菱形的边长为 cm.
已知:如图, △A'B'C'和 △ABC中,∠A' =∠A,A'B':AB = A'C':AC
求证:△A'B'C' ∽ △ABC
证明:在△ABC 的边AB、AC(或它们的延长线)上分别截取AD=A'B',AE=A'C',连结DE,因∠A ' =∠A,这样△A'B'C' ≌ △ADE
∴ DE//BC
∴ △ADE ∽ △ABC
∴ △A'B'C' ∽ △ABC
A'
B'
C'
A
B
C
D
E
∵
又 ∠A=∠A'
∴ △ABC∽△A'B'C'
已知∠A=120°,AB=7cm,AC=14cm,∠A'=120°,A'B' =3cm,A'C' =6cm,判断△ABC与△ A′B′C′是否相似,
并说明理由.
四.利用两边成比例且夹角相等识别三角形相似
两三角形的相似比是多少?
△ABC∽△A'B'C ' .
理由如下:
解:
∴
已知∠A=40°,AB=8,AC=15, ∠A' =40°,A'B' =16,A'C' =30 ,判断△ABC与△A'B'C'是否相似,并说明理由.
解:
∴△ABC∽△A'B'C'.
△ABC∽△A'B'C' .
理由如下:
∴ .
∠A=∠A',
又∵
∵ , ,
解:∵ AE=1.5,AC=2,
A
C
B
E
D
如图,D,E分别是 △ABC 的边 AC,AB 上的点,
AE=1.5,AC=2,BC=3,且 ,求 DE 的长.
∴
又∵∠EAD=∠CAB,∴ △ADE ∽△ABC,
∴
∴
五.利用三角形相似求线段的长度
提示:解题时要找准对应边.
证明: ∵ CD 是边 AB 上的高,
∴ ∠ADC =∠CDB =90°.
∴△ADC ∽△CDB,∴ ∠ACD =∠B,
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
A
B
C
D
例 如图,在 △ABC 中,CD 是边 AB 上的高,且 ,求证 :∠ACB=90°.
∵
六.利用三角形相似求角度
方法总结:解题时需注意隐含条件,如垂直关系,三角形的高等.
如图,已知在△ABC 中,∠C=90°,D、E 分别是AB、AC 上的点,AE:AD=AB:AC.
试问:DE 与AB 垂直吗 为什么
A
B
C
D
E
证明:DE⊥AB.理由如下:
∵ AE:AD=AB:AC,
∴ .
又 ∠A=∠A,
∴ △ABC∽△AED.
∴ ∠ADE=∠C=90°.
∴ DE 与AB 垂直.
在 △ABC 和 △DEF 中,∠C =∠F=70°,AC = 3.5 cm,
BC = 2.5 cm,DF =2.1 cm,EF =1.5 cm.
求证:△DEF∽△ABC.
A
C
B
F
E
D
证明:∵ AC = 3.5 cm,BC = 2.5 cm,DF = 2.1 cm,EF = 1.5 cm,
又 ∵∠C =∠F = 70°,∴ △DEF ∽△ABC.
∴
如图,△ABC 与 △ADE 都是等腰三角形,AD=AE, AB=AC,∠DAB=∠CAE. 求证:△ABC ∽△ADE.
证明:∵ AD =AE,AB = AC,
∴
又 ∵∠DAB = ∠CAE,
∴ ∠DAB +∠BAE = ∠CAE +∠BAE,
即 ∠DAE =∠BAC,∴△ABC ∽ △ADE.
A
B
C
D
E
A
B
C
D
解:∵AB=6,BC=4,AC=5, ,
∴
又∵∠B=∠ACD,∴ △ABC ∽ △DCA,
∴ ,
∴
如图,在四边形 ABCD 中,已知 ∠B =∠ACD, AB=6,BC=4,AC=5, ,求 AD 的长.
例 如图所示,在△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,判断这两个三角形是否相似.
C'
B'
A'
C
B
A
解:∵ ∠B=∠B′=90°,
∠A=∠A′,
∴ △ABC∽△A′B′C′.
七.利用两角相等判断三角形相似
弦AB和CD相交于⊙O内一点P,求证:PA·PB=PC·PD.
A
C
D
证明:连接AC、BD.
∵∠A、∠D都是弧CB所对的圆周角,
∴ ∠A=∠D.
同理: ∠C=∠B.
∴△PAC∽△PDB.
即PA·PB=PC·PD.
A
B
P
O
O
D
C
B
P
八.利用三角形相似求等积式
∴ .
∴
解:∵ ED⊥AB,∴∠EDA=90°.
又∠C=90 °,∠A=∠A,
∴ △AED ∽△ABC.
如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D. 求AD的长.
D
A
B
C
E
∴
九.两直角三角形相似的判定
证明:∵ 在△ ABC中,∠A=40°,∠B=80°,
∴ ∠C=180°-∠A-∠B=60°.
∵ 在△DEF中,∠E=80°,∠F=60°.
∴ ∠B=∠E,∠C=∠F.
∴ △ABC ∽△DEF.
如图,△ABC 和 △DEF 中,∠A=40°,∠B=80°,∠E=80 °,∠F=60 ° .求证:△ABC ∽△DEF.
A
C
B
F
E
D
证明:∵ △ABC 的高AD、BE交于点F,
∴ ∠FEA=∠FDB=90°,
∠AFE =∠BFD (对顶角相等)
∴ △FEA ∽ △ FDB,
∴
如图,△ABC 的高 AD、BE 交于点 F.
求证:
D
C
A
B
E
F
解:∵ ∠ A= ∠ A,∠ABD=∠C,
∴ △ABD ∽ △ACB ,
∴ AB : AC=AD : AB,
∴ AB2 = AD · AC.
∵ AD=2, AC=8,
∴ AB =4.
已知:如图,∠ABD=∠C,AD=2, AC=8,求AB.
A
B
C
D
如图,BE是△ABC的外接圆O的直径,CD是△ABC 的高, 求证:AC · BC = BE · CD.
O
D
C
B
A
E
证明: 连接CE,
又∵BE是△ABC的外接圆O的直径,
∴∠BCE= 90°=∠ADC,
∴ ∴ AC · BC = BE · CD.
∴△ACD∽△EBC.
∵∠A=∠E,∠BCE=∠ADC,
则∠A=∠E.
相似三角形对应高的比等于相似比
证明:
∵△ A′B′C′∽△ABC,
∴ ∠B′= ∠B.
又∵ ∠A'D′B' =∠ADB =90°,
∴△A′B′D′∽△ABD.
从而 .
如图,△A′B′C′ ∽△ABC,相似比为k,分别作BC,B′C′上的高AD,A′D′.
求证:
证明:∵△ABC∽△DEF.
相似三角形对应中线的比等于相似比.
A
B
C
M
D
E
F
N
又∵AM、DN分别是△ABC和△DEF的中线.
∴△ABM∽△DEN.
求证:
已知:
△ABC∽△DEF. AM、DN分别为中线.
∴BC=2BM,EF=2EN,
∴
∴
∴∠B =∠E,
证明:∵△ABC∽△DEF.
∴∠B =∠E, ∠BAC=∠EDF.
又∵AM、DN分别是∠BAC和∠EDF的角平分线.
相似三角形对应角平分线的比等于相似比.
A
B
C
M
D
E
F
N
求证:
已知:
△ABC∽△DEF. AM、DN分别为角平分线.
∴
∴∠BAM=∠EDN.
∴△AMB∽△DNE.
∴ , ,
解:∵ △ABC ∽△DEF,
D
E
F
H
例 已知 △ABC∽△DEF,BG、EH 分别是 △ABC和 △DEF 的角平分线,BC = 6 cm,EF = 4cm,BG = 4.8 cm. 求 EH 的长.
∴ .
∴ ,解得 EH = 3.2.
A
G
B
C
故 EH 的长为 3.2 cm.
十.利用相似三角形对应线段的比求线段的长度
相似三角形周长的比等于相似比.
已知:
求证:
证明1:
∴ .
∴
(等比性质).
A
C
B
B′
A′
C′
∵△ABC ∽△A′B′C′,
△ABC ∽△A′B′C′.
A
B
C
证明2:
∴AB=kA′B′,BC=kB′C′,AC=kA′C′
相似三角形的周长比等于相似比.
∵△ABC ∽△A′B′C′,
相似比为k.
∴ .
A′
B′
C′
解:在 △ABC 和 △DEF 中,
∵ AB=2DE,AC=2DF,
又 ∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
A
B
C
D
E
F
∴
如图,在 △ABC 和 △DEF 中,AB = 2 DE ,
AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
十一.利用相似三角形面积的比求面积或线段
A
B
C
D
E
F
面积为
∴△DEF 的边 EF 上的高为 ,
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,
∴ 面积比为 9 : 25.
B
C
A
D
E
解:∵ ∠BAC = ∠DAE,且
十二.利用相似三角形面积的比求多边形的面积(比)
例 如图,D,E 分别是 AC,AB 上的点,已知△ABC 的面积为100 cm2,且 ,求四边形 BCDE 的面积.
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100-36 = 64 (cm2).
如图,这是圆桌正上方的灯泡 (点A ) 发出的光线照射桌面形成阴影的示意图,已知桌面的直径为 1.2米,桌面距离地面为 1 米,若灯泡距离地面 3 米,则地面上阴影部分的面积约为多少 (结果保留两位小数)?
A
D
E
F
C
B
H
解:∵ FH = 1 米,AH = 3 米,桌面的直径为 1.2 米,
∴ AF = AH-FH = 2 (米),DF = 1.2÷2 = 0.6(米).
∵DF∥CH,∴△ADF ∽△ACH,
∴ 即
解得 CH = 0.9米.
(平方米).
答:地面上阴影部分的面积为 2.54 平方米.
∴ 阴影部分的面积为:
A
D
E
F
C
B
H
如图,△ABC 中,点 D、E、F 分别在 AB、AC、BC 上,且 DE∥BC,EF∥AB. 当 D 点为 AB 中点时,求 S四边形BFED : S△ABC 的值.
A
B
C
D
F
E
解:∵ DE∥BC,D 为 AB 中点,
∴ △ADE ∽ △ABC ,
相似比为 1 : 2,
因此面积比为 1 : 4.
∴
A
B
C
D
F
E
又∵ EF∥AB,
∴ △EFC ∽ △ABC ,相似比为 1 : 2,
面积比为 1 : 4.
设 S△ABC= 4,则 S△ADE = 1,S△EFC = 1,
S四边形BFED = S△ABC-S△ADE-S△EFC = 4-1-1 = 2,
∴ S四边形BFED : S△ABC = 2 :4 = .
如图,△ABC 中,DE∥BC,DE 分别交 AB、AC 于点 D、E,S△ADE=2 S△DCE,求 S△ADE ∶S△ABC
解:过点 D 作 AC 的垂线,交点为 F,则
∴
又∵ DE∥BC,∴ △ADE ∽△ABC.
A
B
C
D
E
F
∴
即 S△ADE : S△ABC =4 : 9.
A
B
C
D
E
F
据史料记者,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图,如果木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.
解:太阳光是平行光线,因此∠BAO=∠EDF.
又∠AOB=∠DFE=90°,
∴ △ABO∽△DEF.
因此金字塔的高为134m.
十二.利用相似三角形测物体的高
怎样测出OA的长?
∴ ,
∴
在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一栋高楼的影长为90m,这栋高楼的高度是多少?
∵△ABC ∽ △A'B'C',
解得 A'C'=54m.
答:这栋高楼的高度是54m.
解:
A
B
C
1.8m
3m
A'
B'
C'
90m
∴ ,
即 .
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,
ST=90m,QR=60m,求河的宽度PQ.
解:∵∠PQR=∠PST=90°,∠P=∠P,
解得PQ=90.
P
Q
R
S
T
a
b
∴ △PQR∽△PST.
因此,河宽大约为90m.
十三.利用相似三角形测物体的宽
∴ ,
即 ,
已知左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树底部的距离BD=5m.一个人估计自己眼睛距地面1.6m.她沿着正对这两棵树的一条水平直路l 从左向右前进,当她与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C了?
分析:如图(1),设观察者眼睛的位置为点F,画出观察者的水平视线FG,分别交AB、CD于点H、K.视线FA、FG的夹角∠AFH是观察点A时的仰角.类似地,∠CFK是观察点C时的仰角.由于树的遮挡,区域Ⅰ和Ⅱ都在观察者看不到的区域(盲区)之内.
十四.利用相似三角形测量有遮挡的物体
图(1)
仰角
水平线
视线
解:如图(2),假设观察者从左向右走到点E时,她的眼睛的位置点E与两棵树顶端点A、C恰在一条直线上.
由题意可知,AB⊥l,CD⊥l,
∴ AB∥CD,△AEH∽△CEK.
即 .
解得 EH=8(m).
由此可知,如果观察者继续前进,即她与左边树的距离小于8m时,由于这棵树的遮挡,右边树的顶端点C在观察者的盲区之内,观察者看不到它.
图(2)
∴ ,
如图,△OAB和△OCD是位似图形,AB与CD平行吗?
为什么?
O
A
B
C
D
解:AB∥CD.
∵△OAB与△ODC是位似图形,
∴△OAB∽△OCD.
∴∠OAB=∠C.
∴ AB∥CD.
相似图形经典例题
例 如图,四边形 ABCD 和 EFGH 相似,求角α,β的大小和EH的长度 x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
一.利用相似多边形的定义求线段、角的值
在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°.
解:∵ 四边形 ABCD 和 EFGH 相似,
∴ 它们的对应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
∵ 四边形ABCD和EFGH相似,
∴它们的对应边成比例,由此可得
解得 x = 28 .
,即 .
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
如图所示的两个五边形相似,求未知边a、b、c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
解:相似多边形的对应边的比相等,由此可得
, , , ,
解得:a=3,b=4.5,c=4,d=6.
所以未知边a,b,c,d的长度分别为3,4.5,4,6.
如图,把矩形 ABCD 对折,折痕为 EF,若矩形ABCD 与矩形 EABF 相似,AB = 1.
A
B
C
D
E
F
解:∵ E 是 AD 的中点,
∴ .
又∵矩形 ABCD 与矩形 EABF相似,AB=1,
∴ ,
∴ AB2 = AE·BC,
∴ .
解得
(1)求BC长;
(2)求矩形 ABFE 与矩形 ABCD 的相似比.
A
B
C
D
E
F
解:矩形 ABEF 与矩形ABCD
的相似比为:
如图,l1∥l2∥l3, ,DE=6,求DF的长.
解:∵l1∥l2∥l3,
∴ .
又∵ ,DE=6,
∴ ,
解得EF=4.
∴DF=DE+EF=6+4=10.
l1
l2
l3
例 如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD.
∴AE=3.
解:∵AC=4,EC=1,
∵ DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
二.利用平行线分线段成比例定理及推论求线段长度
A
B
C
D
E
证明:在△ADE与△ABC中,
∠A= ∠A.
∵ DE//BC,
∴∠ADE=∠B, ∠AED=∠C,
过E作EF//AB交BC于F,
∵四边形DBFE是平行四边形,
F
∴DE=BF .
∴△ADE∽△ABC .
∴ .
∴ .
则
已知:如图,在△ABC中,DE//BC,且DE分别交AB , AC于点D、E.
求证:△ADE∽△ABC .
如图,在△ABC中, EF∥BC.
( 1 )如果E、F分别是 AB 和 AC 上的点, AE = BE=7,
FC = 4 ,那么 AF 的长是多少?
A
B
C
E
F
解:∵
∴
解得 AF = 4.
(2) 如果AB = 10,AE=6,AF = 5,那么 FC 的长是多少?
解:∵
∴
解得 .
A
B
C
E
F
如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.
求证:OD∶OA=OE∶OB
证明: ∵ DF∥AC,
∵ EF∥BC,
如图,已知菱形 ABCD 内接于△AEF,AE=5cm, AF = 4 cm,求菱形的边长.
解:∵ 四边形 ABCD 为菱形,
B
C
A
D
E
F
∴CD∥AB,
∴
设菱形的边长为 x cm,则CD
= AD = x cm,DF = (4-x )cm,
∴ 解得 ∴菱形的边长为 cm.
已知:如图, △A'B'C'和 △ABC中,∠A' =∠A,A'B':AB = A'C':AC
求证:△A'B'C' ∽ △ABC
证明:在△ABC 的边AB、AC(或它们的延长线)上分别截取AD=A'B',AE=A'C',连结DE,因∠A ' =∠A,这样△A'B'C' ≌ △ADE
∴ DE//BC
∴ △ADE ∽ △ABC
∴ △A'B'C' ∽ △ABC
A'
B'
C'
A
B
C
D
E
∵
又 ∠A=∠A'
∴ △ABC∽△A'B'C'
已知∠A=120°,AB=7cm,AC=14cm,∠A'=120°,A'B' =3cm,A'C' =6cm,判断△ABC与△ A′B′C′是否相似,
并说明理由.
四.利用两边成比例且夹角相等识别三角形相似
两三角形的相似比是多少?
△ABC∽△A'B'C ' .
理由如下:
解:
∴
已知∠A=40°,AB=8,AC=15, ∠A' =40°,A'B' =16,A'C' =30 ,判断△ABC与△A'B'C'是否相似,并说明理由.
解:
∴△ABC∽△A'B'C'.
△ABC∽△A'B'C' .
理由如下:
∴ .
∠A=∠A',
又∵
∵ , ,
解:∵ AE=1.5,AC=2,
A
C
B
E
D
如图,D,E分别是 △ABC 的边 AC,AB 上的点,
AE=1.5,AC=2,BC=3,且 ,求 DE 的长.
∴
又∵∠EAD=∠CAB,∴ △ADE ∽△ABC,
∴
∴
五.利用三角形相似求线段的长度
提示:解题时要找准对应边.
证明: ∵ CD 是边 AB 上的高,
∴ ∠ADC =∠CDB =90°.
∴△ADC ∽△CDB,∴ ∠ACD =∠B,
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
A
B
C
D
例 如图,在 △ABC 中,CD 是边 AB 上的高,且 ,求证 :∠ACB=90°.
∵
六.利用三角形相似求角度
方法总结:解题时需注意隐含条件,如垂直关系,三角形的高等.
如图,已知在△ABC 中,∠C=90°,D、E 分别是AB、AC 上的点,AE:AD=AB:AC.
试问:DE 与AB 垂直吗 为什么
A
B
C
D
E
证明:DE⊥AB.理由如下:
∵ AE:AD=AB:AC,
∴ .
又 ∠A=∠A,
∴ △ABC∽△AED.
∴ ∠ADE=∠C=90°.
∴ DE 与AB 垂直.
在 △ABC 和 △DEF 中,∠C =∠F=70°,AC = 3.5 cm,
BC = 2.5 cm,DF =2.1 cm,EF =1.5 cm.
求证:△DEF∽△ABC.
A
C
B
F
E
D
证明:∵ AC = 3.5 cm,BC = 2.5 cm,DF = 2.1 cm,EF = 1.5 cm,
又 ∵∠C =∠F = 70°,∴ △DEF ∽△ABC.
∴
如图,△ABC 与 △ADE 都是等腰三角形,AD=AE, AB=AC,∠DAB=∠CAE. 求证:△ABC ∽△ADE.
证明:∵ AD =AE,AB = AC,
∴
又 ∵∠DAB = ∠CAE,
∴ ∠DAB +∠BAE = ∠CAE +∠BAE,
即 ∠DAE =∠BAC,∴△ABC ∽ △ADE.
A
B
C
D
E
A
B
C
D
解:∵AB=6,BC=4,AC=5, ,
∴
又∵∠B=∠ACD,∴ △ABC ∽ △DCA,
∴ ,
∴
如图,在四边形 ABCD 中,已知 ∠B =∠ACD, AB=6,BC=4,AC=5, ,求 AD 的长.
例 如图所示,在△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,判断这两个三角形是否相似.
C'
B'
A'
C
B
A
解:∵ ∠B=∠B′=90°,
∠A=∠A′,
∴ △ABC∽△A′B′C′.
七.利用两角相等判断三角形相似
弦AB和CD相交于⊙O内一点P,求证:PA·PB=PC·PD.
A
C
D
证明:连接AC、BD.
∵∠A、∠D都是弧CB所对的圆周角,
∴ ∠A=∠D.
同理: ∠C=∠B.
∴△PAC∽△PDB.
即PA·PB=PC·PD.
A
B
P
O
O
D
C
B
P
八.利用三角形相似求等积式
∴ .
∴
解:∵ ED⊥AB,∴∠EDA=90°.
又∠C=90 °,∠A=∠A,
∴ △AED ∽△ABC.
如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D. 求AD的长.
D
A
B
C
E
∴
九.两直角三角形相似的判定
证明:∵ 在△ ABC中,∠A=40°,∠B=80°,
∴ ∠C=180°-∠A-∠B=60°.
∵ 在△DEF中,∠E=80°,∠F=60°.
∴ ∠B=∠E,∠C=∠F.
∴ △ABC ∽△DEF.
如图,△ABC 和 △DEF 中,∠A=40°,∠B=80°,∠E=80 °,∠F=60 ° .求证:△ABC ∽△DEF.
A
C
B
F
E
D
证明:∵ △ABC 的高AD、BE交于点F,
∴ ∠FEA=∠FDB=90°,
∠AFE =∠BFD (对顶角相等)
∴ △FEA ∽ △ FDB,
∴
如图,△ABC 的高 AD、BE 交于点 F.
求证:
D
C
A
B
E
F
解:∵ ∠ A= ∠ A,∠ABD=∠C,
∴ △ABD ∽ △ACB ,
∴ AB : AC=AD : AB,
∴ AB2 = AD · AC.
∵ AD=2, AC=8,
∴ AB =4.
已知:如图,∠ABD=∠C,AD=2, AC=8,求AB.
A
B
C
D
如图,BE是△ABC的外接圆O的直径,CD是△ABC 的高, 求证:AC · BC = BE · CD.
O
D
C
B
A
E
证明: 连接CE,
又∵BE是△ABC的外接圆O的直径,
∴∠BCE= 90°=∠ADC,
∴ ∴ AC · BC = BE · CD.
∴△ACD∽△EBC.
∵∠A=∠E,∠BCE=∠ADC,
则∠A=∠E.
相似三角形对应高的比等于相似比
证明:
∵△ A′B′C′∽△ABC,
∴ ∠B′= ∠B.
又∵ ∠A'D′B' =∠ADB =90°,
∴△A′B′D′∽△ABD.
从而 .
如图,△A′B′C′ ∽△ABC,相似比为k,分别作BC,B′C′上的高AD,A′D′.
求证:
证明:∵△ABC∽△DEF.
相似三角形对应中线的比等于相似比.
A
B
C
M
D
E
F
N
又∵AM、DN分别是△ABC和△DEF的中线.
∴△ABM∽△DEN.
求证:
已知:
△ABC∽△DEF. AM、DN分别为中线.
∴BC=2BM,EF=2EN,
∴
∴
∴∠B =∠E,
证明:∵△ABC∽△DEF.
∴∠B =∠E, ∠BAC=∠EDF.
又∵AM、DN分别是∠BAC和∠EDF的角平分线.
相似三角形对应角平分线的比等于相似比.
A
B
C
M
D
E
F
N
求证:
已知:
△ABC∽△DEF. AM、DN分别为角平分线.
∴
∴∠BAM=∠EDN.
∴△AMB∽△DNE.
∴ , ,
解:∵ △ABC ∽△DEF,
D
E
F
H
例 已知 △ABC∽△DEF,BG、EH 分别是 △ABC和 △DEF 的角平分线,BC = 6 cm,EF = 4cm,BG = 4.8 cm. 求 EH 的长.
∴ .
∴ ,解得 EH = 3.2.
A
G
B
C
故 EH 的长为 3.2 cm.
十.利用相似三角形对应线段的比求线段的长度
相似三角形周长的比等于相似比.
已知:
求证:
证明1:
∴ .
∴
(等比性质).
A
C
B
B′
A′
C′
∵△ABC ∽△A′B′C′,
△ABC ∽△A′B′C′.
A
B
C
证明2:
∴AB=kA′B′,BC=kB′C′,AC=kA′C′
相似三角形的周长比等于相似比.
∵△ABC ∽△A′B′C′,
相似比为k.
∴ .
A′
B′
C′
解:在 △ABC 和 △DEF 中,
∵ AB=2DE,AC=2DF,
又 ∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
A
B
C
D
E
F
∴
如图,在 △ABC 和 △DEF 中,AB = 2 DE ,
AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
十一.利用相似三角形面积的比求面积或线段
A
B
C
D
E
F
面积为
∴△DEF 的边 EF 上的高为 ,
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,
∴ 面积比为 9 : 25.
B
C
A
D
E
解:∵ ∠BAC = ∠DAE,且
十二.利用相似三角形面积的比求多边形的面积(比)
例 如图,D,E 分别是 AC,AB 上的点,已知△ABC 的面积为100 cm2,且 ,求四边形 BCDE 的面积.
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100-36 = 64 (cm2).
如图,这是圆桌正上方的灯泡 (点A ) 发出的光线照射桌面形成阴影的示意图,已知桌面的直径为 1.2米,桌面距离地面为 1 米,若灯泡距离地面 3 米,则地面上阴影部分的面积约为多少 (结果保留两位小数)?
A
D
E
F
C
B
H
解:∵ FH = 1 米,AH = 3 米,桌面的直径为 1.2 米,
∴ AF = AH-FH = 2 (米),DF = 1.2÷2 = 0.6(米).
∵DF∥CH,∴△ADF ∽△ACH,
∴ 即
解得 CH = 0.9米.
(平方米).
答:地面上阴影部分的面积为 2.54 平方米.
∴ 阴影部分的面积为:
A
D
E
F
C
B
H
如图,△ABC 中,点 D、E、F 分别在 AB、AC、BC 上,且 DE∥BC,EF∥AB. 当 D 点为 AB 中点时,求 S四边形BFED : S△ABC 的值.
A
B
C
D
F
E
解:∵ DE∥BC,D 为 AB 中点,
∴ △ADE ∽ △ABC ,
相似比为 1 : 2,
因此面积比为 1 : 4.
∴
A
B
C
D
F
E
又∵ EF∥AB,
∴ △EFC ∽ △ABC ,相似比为 1 : 2,
面积比为 1 : 4.
设 S△ABC= 4,则 S△ADE = 1,S△EFC = 1,
S四边形BFED = S△ABC-S△ADE-S△EFC = 4-1-1 = 2,
∴ S四边形BFED : S△ABC = 2 :4 = .
如图,△ABC 中,DE∥BC,DE 分别交 AB、AC 于点 D、E,S△ADE=2 S△DCE,求 S△ADE ∶S△ABC
解:过点 D 作 AC 的垂线,交点为 F,则
∴
又∵ DE∥BC,∴ △ADE ∽△ABC.
A
B
C
D
E
F
∴
即 S△ADE : S△ABC =4 : 9.
A
B
C
D
E
F
据史料记者,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图,如果木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.
解:太阳光是平行光线,因此∠BAO=∠EDF.
又∠AOB=∠DFE=90°,
∴ △ABO∽△DEF.
因此金字塔的高为134m.
十二.利用相似三角形测物体的高
怎样测出OA的长?
∴ ,
∴
在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一栋高楼的影长为90m,这栋高楼的高度是多少?
∵△ABC ∽ △A'B'C',
解得 A'C'=54m.
答:这栋高楼的高度是54m.
解:
A
B
C
1.8m
3m
A'
B'
C'
90m
∴ ,
即 .
如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,
ST=90m,QR=60m,求河的宽度PQ.
解:∵∠PQR=∠PST=90°,∠P=∠P,
解得PQ=90.
P
Q
R
S
T
a
b
∴ △PQR∽△PST.
因此,河宽大约为90m.
十三.利用相似三角形测物体的宽
∴ ,
即 ,
已知左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树底部的距离BD=5m.一个人估计自己眼睛距地面1.6m.她沿着正对这两棵树的一条水平直路l 从左向右前进,当她与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C了?
分析:如图(1),设观察者眼睛的位置为点F,画出观察者的水平视线FG,分别交AB、CD于点H、K.视线FA、FG的夹角∠AFH是观察点A时的仰角.类似地,∠CFK是观察点C时的仰角.由于树的遮挡,区域Ⅰ和Ⅱ都在观察者看不到的区域(盲区)之内.
十四.利用相似三角形测量有遮挡的物体
图(1)
仰角
水平线
视线
解:如图(2),假设观察者从左向右走到点E时,她的眼睛的位置点E与两棵树顶端点A、C恰在一条直线上.
由题意可知,AB⊥l,CD⊥l,
∴ AB∥CD,△AEH∽△CEK.
即 .
解得 EH=8(m).
由此可知,如果观察者继续前进,即她与左边树的距离小于8m时,由于这棵树的遮挡,右边树的顶端点C在观察者的盲区之内,观察者看不到它.
图(2)
∴ ,
如图,△OAB和△OCD是位似图形,AB与CD平行吗?
为什么?
O
A
B
C
D
解:AB∥CD.
∵△OAB与△ODC是位似图形,
∴△OAB∽△OCD.
∴∠OAB=∠C.
∴ AB∥CD.
