人教版八下第十七章勾股定理经典题型讲解(63张ppt)
文档属性
| 名称 | 人教版八下第十七章勾股定理经典题型讲解(63张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 18:56:06 | ||
图片预览








文档简介
(共63张PPT)
勾股定理经典题型讲解
如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
C
A
B
一.利用勾股定理求直角三角形的边长
c
b
a
设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
解:由勾股定理得52+122=c2 ,
c=13;
解:由勾股定理得62+b2=102,
b=8;
解:由勾股定理得a2+152=252 ,
a=20.
a
c
b
a
b
c
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
在Rt△ABC中, ∠C=90°.
解:
(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52,
解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得
提示:已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
二.勾股定理和方程相结合求直角三角形的边长
(舍去)
(舍去)
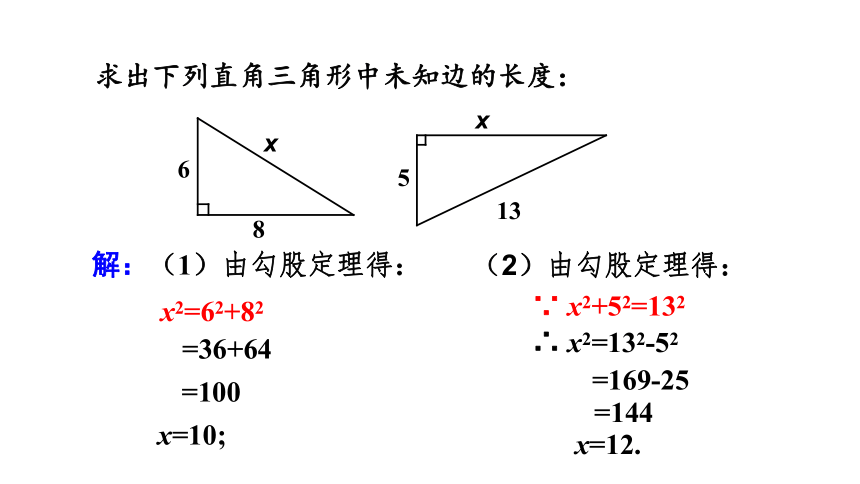
求出下列直角三角形中未知边的长度:
6
8
x
5
x
13
解:(1)由勾股定理得:
=36+64
=100
x2=62+82
x=10;
∵ x2+52=132
∴ x2=132-52
=169-25
=144
x=12.
(2)由勾股定理得:
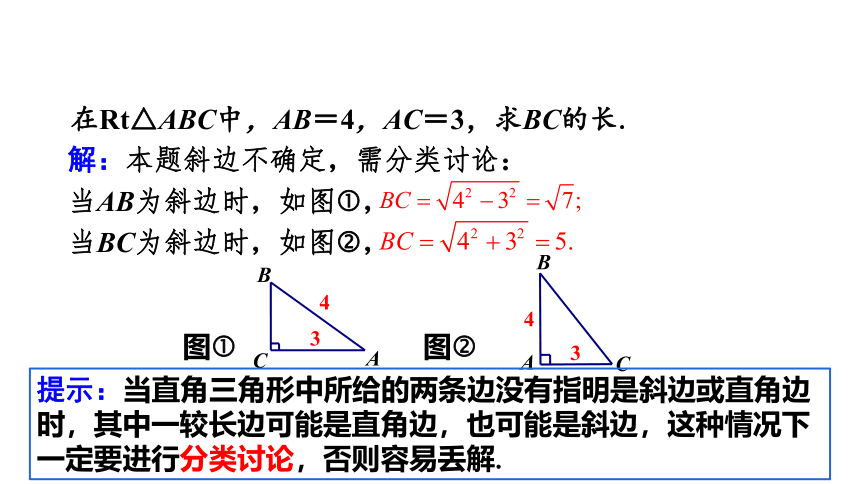
在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
提示:当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
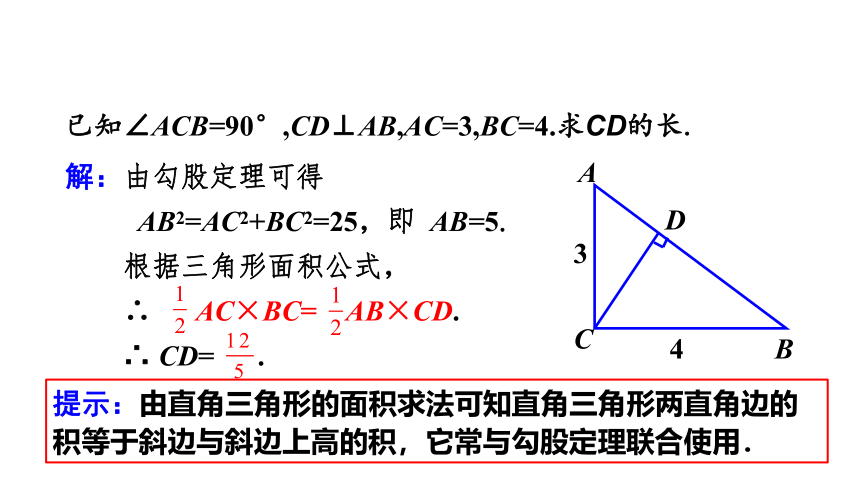
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,即 AB=5.
根据三角形面积公式,
∴ AC×BC= AB×CD.
∴ CD= .
A
D
B
C
3
4
提示:由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
已知条件有哪些?
三.勾股定理解决线段长度问题
【思考】
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
不能.
3.怎样判定这块木板能否通过木框?
求出斜边的长,与木板的宽比较.
小于AC即可.
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为AC大于木板的宽2.2 m,所
以木板能从门框内通过.
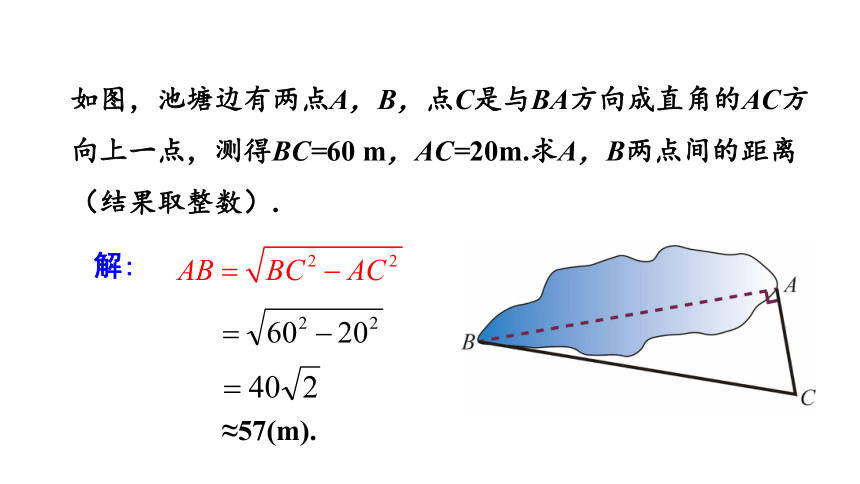
如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60 m,AC=20m.求A,B两点间的距离(结果取整数).
解:
≈57(m).
如图,一架2.6米长的梯子AB 斜靠在一竖直的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5
米,那么梯子底端B也外移0.5米吗?
四.勾股定理解决线段移动问题
C
O
D
B
A
(2)在Rt△COD中,根据勾股定理,
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15.
解:(1)在Rt△AOB中,根据勾股定理,
OB2=AB2-OA2=2.62-2.42=1.
OB=1.
答:梯子的底端B距墙角O为1米.
答:梯子底端B也外移约0.77米.
我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题.
译:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面一尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.这个水池的深度与这根芦苇的长度分别是多少?
A
B
C
A
B
C
解:设AB=x,则AC=x+1,
有 AB2+BC2=AC2,
可列方程,得 x2+52=(x+1)2 ,
解方程得x=12.
因此x+1=13
答:这个水池的深度是12尺,
这根芦苇的长度是13尺.
C
如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )
A. B. C. D.
解析:把圆柱侧面展开,展开图如图所示,点A、C的最短距离为线段AC的长.
在Rt△ADC中,∠ADC=90°,CD=AB=3,AD为底面半圆弧长,AD=1.5π,所以AC= ,
故选:C.
5
无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有_____cm.
解析:由题意可得:杯子内的筷子长度最长为: =15,
则筷子露在杯子外面的筷子长度最少为:20﹣15=5(cm).
求出下列直角三角形中未知的边.
AC=8
AB=17
A
B
C
6
10
A
B
C
8
15
A
B
C
2
30°
A
B
C
2
45°
直角三角形中,以直角边为边长的两个正方形面积为7和8,
则以斜边为边长的正方形的面积为 .
15
如图,在平面直角坐标系中有两点A(5,0)和B(0,4),求这两点间的距离.
解:在Rt△AOB中,∵OA=5,OB=4,
∴A、B两点间的距离为 .
∴AB2=OA2+OB2=52+42=41,
∴AB= .
一木杆在离地面3米处折断,木杆顶端落在离木杆底端4米处.木杆折断之前有多高?
解:由题意可知,在Rt△RPQ中,
∵PR=3,PQ=4,
∴RQ2=PR2+PQ2=32+42=25,
∴RQ=5,PR+RQ=3+5=8.
∴木杆折断之前有8米高.
R
P
Q
如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km, CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
C
A
E
B
D
x
25-x
解:设AE= x km,
根据勾股定理,得
AD2+AE2=DE2,
BC2+BE2=CE2.
又 ∵ DE=CE,
∴ AD2+AE2= BC2+BE2.
即 152+x2=102+(25-x)2
答:E站应建在离A站10km处.
∴ x=10.
则 BE=(25-x)km,
15
10
在△ABC中,若AC=15,BC=13,AB边上的高CD=12,则△ABC的周长为( )
A.32 B.42
C.32或42 D.以上都不对
C
解析:如图①,CD在△ABC内部时,AB=AD+BD=9+5=14,此时,△ABC的周长=14+13+15=42,如图②,CD在△ABC 外部时,AB=AD-BD=9-5=4,此时,△ABC的周长=4+13+15=32.综上所述,△ABC的周长为32或42.故选C.
A
B
A
B
C
2
1
提示: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形(如图).
B
如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( )
A.3 B . C.2 D.1
2
1
在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
五.证明“HL”
已知:如图,在Rt△ABC 和Rt△A′B′ C′中,
∠C=∠C′=90°,AB=A′B ′,AC=A′C′ .
求证:△ABC≌△ A′B′ C′ .
A
B
C
A
B
C′
′
′
′
′
′
′
′
′
证明:在Rt△ABC 和Rt△A ′B′ C′中,∠C=∠C′=90°,
根据勾股定理,得
A
B
C
A
B
C′
′
′
∵ AB=A′B′ ,
AC=A′C′ ,
∴ BC=B′C′ .
∴ △ ABC≌ △A ′B′ C′ (SSS).
-1 0 1 2 3
问题1 你能在数轴上表示出 的点吗? 呢?
用同样的方法作 呢?
六.利用勾股定理在数轴上确定无理数
提示:可以构造直角三角形作出边长为无理数的边,就能在数轴上画出表示该无理数的点.
【讨论】根据上面问题你能在数轴上画出表示 的点吗?
√
√
问题2 长为 的线段是直角边的长都为正整数的直角三角形的斜边吗?
0
1
2
3
4
步骤:
l
A
B
C
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C
点,则点C即为表示 的点.
O
也可以使OA=2,AB=3,同样可以求出C点.
0
1
2
3
4
l
A
B
C
七.利用勾股定理在数轴上确定无理数的点
在数轴上作出表示 的点.
作法:
(1)在数轴上找到点A,使OA=1;
(2)过点A作直线垂直于OA,在直线上取点B,
使AB=4,那么OB= ;
(3)以原点O为圆心,以OB为半径作
弧,弧与数轴交于点C,则OC= .
如图,在数轴上,点C为表示 的点.
在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中以A出发分别画出长度为 的线段AB.
B
B
B
八.利用勾股定理在网格上做长度为无理数的线段
A
.
A
.
A
.
如图是由4个边长为1的正方形构成的田字格,只用没有刻度的直尺在这个田字格中最多可以作出多少条长度为 的线段?
解:如图所示,有8条.
九.利用勾股定理在网格上作线段
一个点一个点地找,不要漏解.
如图,在5×5正方形网格中,每个小正方形的边长均为1,画出一个三角形的长分别为 .
A
B
C
解:如图所示.
A′
B′
如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=3,求AM的长.
解:连接BM,MB′.设AM=x,
在Rt△ABM中,AB2+AM2=BM2.
在Rt△MDB′中,MD2+DB′2=MB′2.
∵MB=MB′,∴AB2+AM2=MD2+DB′2,
即92+x2=(9-x)2+(9-3)2,
解得x=2.即AM=2.
十.利用勾股定理在折叠问题中求线段的长度
如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
解:在Rt△ABF中,由勾股定理得 BF2=AF2-AB2=102-82=36,
∴BF=6cm.∴CF=BC-BF=4cm.
设EC=xcm,则EF=DE=(8-x)cm ,
在Rt△ECF中,根据勾股定理
得x2+ 42=(8-x)2,
解得 x=3.
即EC的长为3cm.
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,求重叠部分△AFC的面积.
解:易证△AFD′≌△CFB(AAS), ∴D′F=BF,
设D′F=x,则AF=8-x,
在Rt△AFD′中,AF2=D′F2+AD′2,
(8-x)2=x2+42,
∴S△AFC= AF BC=10.
∴AF=AB-FB=8-3=5,
解得x=3.
如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边为1和2,
∴斜边长为 ,即-1到A的距离是 ,
∴点A所表示的数为 .
提示:求点表示的数时注意画弧的起点不从原点起,因而所表示的数不是斜边长.
在△ABC中,AB、BC、AC三边的长分别为 ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
解:
解:如图,
若△ABC三边的长分别为 (a>0),请利用图中的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
∴△ABC即为所求,
A
B
C
据说,古埃及人曾用如图所示的方法画直角.
这种方法对吗?
十一.勾股定理的逆定理
3
4
5
三边分别为3,4,5,
满足关系:32+42=52,
则该三角形是直角三角形.
已知:如图,在△ABC中,AB=c,BC=a,CA=b,
并且 .
A
B
b
c
a
b
证明:作 A1B1C1,
在△ABC和△A1B1C 1中,
C
a
求证:∠C=90°.
使∠C1=90°,
根据勾股定理,则有
∠C=∠ C1
=90°.
B
A
B1C1=a,C1A1=b.
A1B1 2=B1C1 2+C1A1 2=a2+b2.
∵a2+b2=c2,
∴A1B1 =c,
∴AB=A1B1.
≌
∴ ABC
A1B1C1.
A1
C1
B1
AB=A1B1.
CA=C1A1,
BC=B1C1,
下面以a,b,c为边长的三角形是不是直角三角形?如果是,
那么哪一个角是直角?
(1) a=15 , b=8 ,c=17;
解:(1)∵152+82=289,172=289,
(2) a=13 ,b=14 ,c=15.
(2)∵132+142=365,152=225,
总结:根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
十一.利用勾股定理的逆定理判断直角三角形
∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形,且∠C是直角.
∴132+142≠152,
不符合勾股定理的逆定理,∴这个三角形不是直角三角形.
若△ABC的三边a,b,c,且a+b=4,ab=1,c= ,
试说明△ABC是直角三角形.
解:∵a+b=4,ab=1,
∴a2+b2=(a+b)2-2ab=16-2=14.
又∵c2=14,
∴a2+b2=c2,
∴△ABC是直角三角形.
十二.勾股定理的逆定理和乘法公式判断三角形
若△ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c.
试判断△ABC的形状.
解:∵ a2+b2+c2+50=6a+8b+10c,
∴ a2-6a+9+b2-8b+16+c2-10c+25=0.
即 (a-3) + (b-4) + (c-5) =0.
∴ a=3, b=4, c=5,
即 a2+b2=c2.
∴△ABC是直角三角形.
写出下列命题的逆命题,并判断其逆命题的真假性.
(1)如果两个角是直角,那么它们相等.
(2)在角的内部,到角的两边距离相等的点在角的平分线上.
(3)如果 ,那么a≥0.
解:(1)如果两个角相等,那么这两个角是直角.假命题.
(2)在角的内部,角的平分线上的点到两边的距离相等.真命题.
(3)如果a≥0,那么 .真命题.
若△ABC的三边a,b,c满足 a:b: c=3:4:5,试判断△ABC的形状.
解:设a=3k,b=4k,c=5k(k>0),
∵(3k)2+(4k)2=25k2,(5k)2=25k2,
∴(3k)2+(4k)2=(5k)2,
∴△ABC是直角三角形,且∠C是直角.
A,B,C三地的两两距离如图所示,A地在B地的正东方向,C地在B地的什么方向?
解:∵AB2+BC2=122+52
=144+25=169,
AC2=132=169,
∴AB2+BC2=AC2,
∴△ABC为直角三角形,且∠B=90°,
由于A地在B地的正东方向,所以C地在B地的正北方向.
解:AF⊥EF.理由如下:
设正方形的边长为4a, 则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,∴△AEF为直角三角形,且AE为斜边.
如图,在正方形ABCD中,F是CD的中点,E为BC上一点,
且CE= CB,试判断AF与EF的位置关系,并说明理由.
∴∠AFE=90°,即AF⊥EF.
1
2
如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
N
E
P
Q
R
十三.利用勾股定理的逆定理解答角度问题
【思考】1.认真读题,找已知是什么?
“远航”号的航向、两艘船的一个半小时后的航程及距离已知,如下图.
1
2
N
E
P
Q
R
16×1.5=24
12×1.5=18
30
.由于我们现在所能得到的都是线段长,要求角,由此我们想到利用什么思想?
要解决的问题是求出两艘船航向所成角.
勾股定理逆定理.
【思考】.需要解决的问题是什么?
转化的思想.
.知道线段长度,通过线段长度来求角的度数,我们可以利用什么转化呢?
解:根据题意得
PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),
QR=30海里.
∵242+182=302,即PQ2+PR2=QR2,∴∠QPR=90°.
由“远航”号沿东北方向航行可知∠1=45°.
∴∠2=45°,即“海天”号沿西北方向航行.
N
E
P
Q
R
1
2
方法点拨:解决实际问题的步骤:①标注有用信息,明确已知和所求;②构建几何模型(从整体到局部);③应用数学知识求解.
在寻找马航MH370航班过程中,两艘搜救舰艇接到消息,在海面上有疑似漂浮目标A、B. 接到消息后,一艘舰艇以16海里/时的速度离开港口O(如图所示)向北偏东40°方向航行,另一艘舰艇在同时以12海里/时的速度向北偏西一定角度的航向行驶,已知它们离港口一个半小时后相距30海里,问另一艘舰艇的航行方向是北偏西多少度?
解:由题意得,OB=12×1.5=18海里,
OA=16×1.5=24海里,
又∵AB=30海里,
∴182+242=302,即OB2+OA2=AB2,
∴∠AOB=90°.
∵∠DOA=40°,
∴∠BOD=50°.
则另一艘舰艇的航行方向是北偏西50°.
如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
解:连接BD.
在Rt△ABD中,由勾股定理得 BD2=AB2+AD2,
∴BD=5cm.又∵ CD=12cm,BC=13cm,
∴ BC2=CD2+BD2,∴△BDC是直角三角形.
∴S四边形ABCD=SRt△BCD-SRt△ABD= BD CD- AB AD = ×(5×12-3×4)=24 (cm2).
C
B
A
D
十四.利用勾股定理的逆定理解答面积问题
如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3cm,BC=4cm,求△ABC的面积.
解: ∵ S△ACD=30 cm2,DC=12 cm.
∴ AC=5 cm.
又∵
∴△ABC是直角三角形, ∠B是直角.
∴
D
C
B
A
如图,是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8m,AD=BC=6m,AC=9m,请你运用所学知识帮他检验一下挖的是否合格?
解:∵AB=DC=8m,AD=BC=6m,
∴AB2+BC2=82+62=64+36=100.
又∵AC2=92=81,
∴AB2+BC2≠AC2,∴∠ABC≠90°,
∴该农民挖的不合格.
十五.利用勾股定理的逆定理解答检测问题
一个零件的形状如图 所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图 所示,这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图
图
在△BCD中,
∴△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
∴△ABD 是直角三角形,∠A是直角.
D
A
B
C
4
3
5
13
12
图
AB2+AD2=32+42=25=52=BD2,
BD2+BC2=52+122=169=132=CD2,
如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:∵出发2小时,A组行了12×2=24(km),
B组行了9×2=18(km),
又∵A,B两组相距30km,
且有242+182=302,
∴A,B两组行进的方向成直角.
A
O
B
在城市街路上速度不得超过70千米/时,一辆小汽车某一时刻行驶在路边车速检测仪的北偏东30°距离30米处,过了2秒后行驶了50米,此时小汽车与车速检测仪间的距离为40米. 问:2秒后小汽车在车速检测仪的哪个方向 这辆小汽车超速了吗
车速检测仪
小汽车
30米
30°
北
60°
解:小汽车在车速检测仪的南偏东60°方向或北偏西60°方向.
25米/秒=90千米/时>70千米/时
∴小汽车超速了.
2秒后
50米
40米
如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
分析:连接AC,把四边形分成两个三角形.先用勾股定理求出AC的长度,再利用勾股定理的逆定理判断△ACD是直角三角形.
A
D
B
C
3
4
13
12
解:连接AC.
在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,
且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
A
D
B
C
3
4
13
12
如图,在△ABC中,AB:BC:CA=3:4:5且周长为36cm,点P从点A开始沿AB边向B点以每秒2cm的速度移动,点Q从点C沿CB边向点B以每秒1cm的速度移动,如果同时出发,则过3s时,求PQ的长.
解:设AB为3xcm,BC为4xcm,AC为5xcm,∵周长为36cm,即AB+BC+AC=36cm,
∴AB=9cm,BC=12cm,AC=15cm.
∵AB2+BC2=AC2,∴△ABC是直角三角形,过3秒时,
BP=9-3×2=3(cm),BQ=12-1×3=9(cm),
在Rt△PBQ中,由勾股定理得
∴3x+4x+5x=36,
解得x=3.
P
C
B
A
Q
勾股定理经典题型讲解
如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
C
A
B
一.利用勾股定理求直角三角形的边长
c
b
a
设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
解:由勾股定理得52+122=c2 ,
c=13;
解:由勾股定理得62+b2=102,
b=8;
解:由勾股定理得a2+152=252 ,
a=20.
a
c
b
a
b
c
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
在Rt△ABC中, ∠C=90°.
解:
(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52,
解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得
提示:已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
二.勾股定理和方程相结合求直角三角形的边长
(舍去)
(舍去)
求出下列直角三角形中未知边的长度:
6
8
x
5
x
13
解:(1)由勾股定理得:
=36+64
=100
x2=62+82
x=10;
∵ x2+52=132
∴ x2=132-52
=169-25
=144
x=12.
(2)由勾股定理得:
在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
提示:当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,即 AB=5.
根据三角形面积公式,
∴ AC×BC= AB×CD.
∴ CD= .
A
D
B
C
3
4
提示:由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
已知条件有哪些?
三.勾股定理解决线段长度问题
【思考】
1.木板能横着或竖着从门框通过吗?
2.这个门框能通过的最大长度是多少?
不能.
3.怎样判定这块木板能否通过木框?
求出斜边的长,与木板的宽比较.
小于AC即可.
解:在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为AC大于木板的宽2.2 m,所
以木板能从门框内通过.
如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60 m,AC=20m.求A,B两点间的距离(结果取整数).
解:
≈57(m).
如图,一架2.6米长的梯子AB 斜靠在一竖直的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5
米,那么梯子底端B也外移0.5米吗?
四.勾股定理解决线段移动问题
C
O
D
B
A
(2)在Rt△COD中,根据勾股定理,
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15.
解:(1)在Rt△AOB中,根据勾股定理,
OB2=AB2-OA2=2.62-2.42=1.
OB=1.
答:梯子的底端B距墙角O为1米.
答:梯子底端B也外移约0.77米.
我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题.
译:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面一尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.这个水池的深度与这根芦苇的长度分别是多少?
A
B
C
A
B
C
解:设AB=x,则AC=x+1,
有 AB2+BC2=AC2,
可列方程,得 x2+52=(x+1)2 ,
解方程得x=12.
因此x+1=13
答:这个水池的深度是12尺,
这根芦苇的长度是13尺.
C
如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )
A. B. C. D.
解析:把圆柱侧面展开,展开图如图所示,点A、C的最短距离为线段AC的长.
在Rt△ADC中,∠ADC=90°,CD=AB=3,AD为底面半圆弧长,AD=1.5π,所以AC= ,
故选:C.
5
无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有_____cm.
解析:由题意可得:杯子内的筷子长度最长为: =15,
则筷子露在杯子外面的筷子长度最少为:20﹣15=5(cm).
求出下列直角三角形中未知的边.
AC=8
AB=17
A
B
C
6
10
A
B
C
8
15
A
B
C
2
30°
A
B
C
2
45°
直角三角形中,以直角边为边长的两个正方形面积为7和8,
则以斜边为边长的正方形的面积为 .
15
如图,在平面直角坐标系中有两点A(5,0)和B(0,4),求这两点间的距离.
解:在Rt△AOB中,∵OA=5,OB=4,
∴A、B两点间的距离为 .
∴AB2=OA2+OB2=52+42=41,
∴AB= .
一木杆在离地面3米处折断,木杆顶端落在离木杆底端4米处.木杆折断之前有多高?
解:由题意可知,在Rt△RPQ中,
∵PR=3,PQ=4,
∴RQ2=PR2+PQ2=32+42=25,
∴RQ=5,PR+RQ=3+5=8.
∴木杆折断之前有8米高.
R
P
Q
如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km, CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
C
A
E
B
D
x
25-x
解:设AE= x km,
根据勾股定理,得
AD2+AE2=DE2,
BC2+BE2=CE2.
又 ∵ DE=CE,
∴ AD2+AE2= BC2+BE2.
即 152+x2=102+(25-x)2
答:E站应建在离A站10km处.
∴ x=10.
则 BE=(25-x)km,
15
10
在△ABC中,若AC=15,BC=13,AB边上的高CD=12,则△ABC的周长为( )
A.32 B.42
C.32或42 D.以上都不对
C
解析:如图①,CD在△ABC内部时,AB=AD+BD=9+5=14,此时,△ABC的周长=14+13+15=42,如图②,CD在△ABC 外部时,AB=AD-BD=9-5=4,此时,△ABC的周长=4+13+15=32.综上所述,△ABC的周长为32或42.故选C.
A
B
A
B
C
2
1
提示: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形(如图).
B
如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( )
A.3 B . C.2 D.1
2
1
在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
五.证明“HL”
已知:如图,在Rt△ABC 和Rt△A′B′ C′中,
∠C=∠C′=90°,AB=A′B ′,AC=A′C′ .
求证:△ABC≌△ A′B′ C′ .
A
B
C
A
B
C′
′
′
′
′
′
′
′
′
证明:在Rt△ABC 和Rt△A ′B′ C′中,∠C=∠C′=90°,
根据勾股定理,得
A
B
C
A
B
C′
′
′
∵ AB=A′B′ ,
AC=A′C′ ,
∴ BC=B′C′ .
∴ △ ABC≌ △A ′B′ C′ (SSS).
-1 0 1 2 3
问题1 你能在数轴上表示出 的点吗? 呢?
用同样的方法作 呢?
六.利用勾股定理在数轴上确定无理数
提示:可以构造直角三角形作出边长为无理数的边,就能在数轴上画出表示该无理数的点.
【讨论】根据上面问题你能在数轴上画出表示 的点吗?
√
√
问题2 长为 的线段是直角边的长都为正整数的直角三角形的斜边吗?
0
1
2
3
4
步骤:
l
A
B
C
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C
点,则点C即为表示 的点.
O
也可以使OA=2,AB=3,同样可以求出C点.
0
1
2
3
4
l
A
B
C
七.利用勾股定理在数轴上确定无理数的点
在数轴上作出表示 的点.
作法:
(1)在数轴上找到点A,使OA=1;
(2)过点A作直线垂直于OA,在直线上取点B,
使AB=4,那么OB= ;
(3)以原点O为圆心,以OB为半径作
弧,弧与数轴交于点C,则OC= .
如图,在数轴上,点C为表示 的点.
在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中以A出发分别画出长度为 的线段AB.
B
B
B
八.利用勾股定理在网格上做长度为无理数的线段
A
.
A
.
A
.
如图是由4个边长为1的正方形构成的田字格,只用没有刻度的直尺在这个田字格中最多可以作出多少条长度为 的线段?
解:如图所示,有8条.
九.利用勾股定理在网格上作线段
一个点一个点地找,不要漏解.
如图,在5×5正方形网格中,每个小正方形的边长均为1,画出一个三角形的长分别为 .
A
B
C
解:如图所示.
A′
B′
如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=3,求AM的长.
解:连接BM,MB′.设AM=x,
在Rt△ABM中,AB2+AM2=BM2.
在Rt△MDB′中,MD2+DB′2=MB′2.
∵MB=MB′,∴AB2+AM2=MD2+DB′2,
即92+x2=(9-x)2+(9-3)2,
解得x=2.即AM=2.
十.利用勾股定理在折叠问题中求线段的长度
如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
解:在Rt△ABF中,由勾股定理得 BF2=AF2-AB2=102-82=36,
∴BF=6cm.∴CF=BC-BF=4cm.
设EC=xcm,则EF=DE=(8-x)cm ,
在Rt△ECF中,根据勾股定理
得x2+ 42=(8-x)2,
解得 x=3.
即EC的长为3cm.
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,求重叠部分△AFC的面积.
解:易证△AFD′≌△CFB(AAS), ∴D′F=BF,
设D′F=x,则AF=8-x,
在Rt△AFD′中,AF2=D′F2+AD′2,
(8-x)2=x2+42,
∴S△AFC= AF BC=10.
∴AF=AB-FB=8-3=5,
解得x=3.
如图,数轴上点A所表示的数为a,求a的值.
解:∵图中的直角三角形的两直角边为1和2,
∴斜边长为 ,即-1到A的距离是 ,
∴点A所表示的数为 .
提示:求点表示的数时注意画弧的起点不从原点起,因而所表示的数不是斜边长.
在△ABC中,AB、BC、AC三边的长分别为 ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
解:
解:如图,
若△ABC三边的长分别为 (a>0),请利用图中的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
∴△ABC即为所求,
A
B
C
据说,古埃及人曾用如图所示的方法画直角.
这种方法对吗?
十一.勾股定理的逆定理
3
4
5
三边分别为3,4,5,
满足关系:32+42=52,
则该三角形是直角三角形.
已知:如图,在△ABC中,AB=c,BC=a,CA=b,
并且 .
A
B
b
c
a
b
证明:作 A1B1C1,
在△ABC和△A1B1C 1中,
C
a
求证:∠C=90°.
使∠C1=90°,
根据勾股定理,则有
∠C=∠ C1
=90°.
B
A
B1C1=a,C1A1=b.
A1B1 2=B1C1 2+C1A1 2=a2+b2.
∵a2+b2=c2,
∴A1B1 =c,
∴AB=A1B1.
≌
∴ ABC
A1B1C1.
A1
C1
B1
AB=A1B1.
CA=C1A1,
BC=B1C1,
下面以a,b,c为边长的三角形是不是直角三角形?如果是,
那么哪一个角是直角?
(1) a=15 , b=8 ,c=17;
解:(1)∵152+82=289,172=289,
(2) a=13 ,b=14 ,c=15.
(2)∵132+142=365,152=225,
总结:根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
十一.利用勾股定理的逆定理判断直角三角形
∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形,且∠C是直角.
∴132+142≠152,
不符合勾股定理的逆定理,∴这个三角形不是直角三角形.
若△ABC的三边a,b,c,且a+b=4,ab=1,c= ,
试说明△ABC是直角三角形.
解:∵a+b=4,ab=1,
∴a2+b2=(a+b)2-2ab=16-2=14.
又∵c2=14,
∴a2+b2=c2,
∴△ABC是直角三角形.
十二.勾股定理的逆定理和乘法公式判断三角形
若△ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c.
试判断△ABC的形状.
解:∵ a2+b2+c2+50=6a+8b+10c,
∴ a2-6a+9+b2-8b+16+c2-10c+25=0.
即 (a-3) + (b-4) + (c-5) =0.
∴ a=3, b=4, c=5,
即 a2+b2=c2.
∴△ABC是直角三角形.
写出下列命题的逆命题,并判断其逆命题的真假性.
(1)如果两个角是直角,那么它们相等.
(2)在角的内部,到角的两边距离相等的点在角的平分线上.
(3)如果 ,那么a≥0.
解:(1)如果两个角相等,那么这两个角是直角.假命题.
(2)在角的内部,角的平分线上的点到两边的距离相等.真命题.
(3)如果a≥0,那么 .真命题.
若△ABC的三边a,b,c满足 a:b: c=3:4:5,试判断△ABC的形状.
解:设a=3k,b=4k,c=5k(k>0),
∵(3k)2+(4k)2=25k2,(5k)2=25k2,
∴(3k)2+(4k)2=(5k)2,
∴△ABC是直角三角形,且∠C是直角.
A,B,C三地的两两距离如图所示,A地在B地的正东方向,C地在B地的什么方向?
解:∵AB2+BC2=122+52
=144+25=169,
AC2=132=169,
∴AB2+BC2=AC2,
∴△ABC为直角三角形,且∠B=90°,
由于A地在B地的正东方向,所以C地在B地的正北方向.
解:AF⊥EF.理由如下:
设正方形的边长为4a, 则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,∴△AEF为直角三角形,且AE为斜边.
如图,在正方形ABCD中,F是CD的中点,E为BC上一点,
且CE= CB,试判断AF与EF的位置关系,并说明理由.
∴∠AFE=90°,即AF⊥EF.
1
2
如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
N
E
P
Q
R
十三.利用勾股定理的逆定理解答角度问题
【思考】1.认真读题,找已知是什么?
“远航”号的航向、两艘船的一个半小时后的航程及距离已知,如下图.
1
2
N
E
P
Q
R
16×1.5=24
12×1.5=18
30
.由于我们现在所能得到的都是线段长,要求角,由此我们想到利用什么思想?
要解决的问题是求出两艘船航向所成角.
勾股定理逆定理.
【思考】.需要解决的问题是什么?
转化的思想.
.知道线段长度,通过线段长度来求角的度数,我们可以利用什么转化呢?
解:根据题意得
PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),
QR=30海里.
∵242+182=302,即PQ2+PR2=QR2,∴∠QPR=90°.
由“远航”号沿东北方向航行可知∠1=45°.
∴∠2=45°,即“海天”号沿西北方向航行.
N
E
P
Q
R
1
2
方法点拨:解决实际问题的步骤:①标注有用信息,明确已知和所求;②构建几何模型(从整体到局部);③应用数学知识求解.
在寻找马航MH370航班过程中,两艘搜救舰艇接到消息,在海面上有疑似漂浮目标A、B. 接到消息后,一艘舰艇以16海里/时的速度离开港口O(如图所示)向北偏东40°方向航行,另一艘舰艇在同时以12海里/时的速度向北偏西一定角度的航向行驶,已知它们离港口一个半小时后相距30海里,问另一艘舰艇的航行方向是北偏西多少度?
解:由题意得,OB=12×1.5=18海里,
OA=16×1.5=24海里,
又∵AB=30海里,
∴182+242=302,即OB2+OA2=AB2,
∴∠AOB=90°.
∵∠DOA=40°,
∴∠BOD=50°.
则另一艘舰艇的航行方向是北偏西50°.
如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
解:连接BD.
在Rt△ABD中,由勾股定理得 BD2=AB2+AD2,
∴BD=5cm.又∵ CD=12cm,BC=13cm,
∴ BC2=CD2+BD2,∴△BDC是直角三角形.
∴S四边形ABCD=SRt△BCD-SRt△ABD= BD CD- AB AD = ×(5×12-3×4)=24 (cm2).
C
B
A
D
十四.利用勾股定理的逆定理解答面积问题
如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3cm,BC=4cm,求△ABC的面积.
解: ∵ S△ACD=30 cm2,DC=12 cm.
∴ AC=5 cm.
又∵
∴△ABC是直角三角形, ∠B是直角.
∴
D
C
B
A
如图,是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8m,AD=BC=6m,AC=9m,请你运用所学知识帮他检验一下挖的是否合格?
解:∵AB=DC=8m,AD=BC=6m,
∴AB2+BC2=82+62=64+36=100.
又∵AC2=92=81,
∴AB2+BC2≠AC2,∴∠ABC≠90°,
∴该农民挖的不合格.
十五.利用勾股定理的逆定理解答检测问题
一个零件的形状如图 所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图 所示,这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图
图
在△BCD中,
∴△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
∴△ABD 是直角三角形,∠A是直角.
D
A
B
C
4
3
5
13
12
图
AB2+AD2=32+42=25=52=BD2,
BD2+BC2=52+122=169=132=CD2,
如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:∵出发2小时,A组行了12×2=24(km),
B组行了9×2=18(km),
又∵A,B两组相距30km,
且有242+182=302,
∴A,B两组行进的方向成直角.
A
O
B
在城市街路上速度不得超过70千米/时,一辆小汽车某一时刻行驶在路边车速检测仪的北偏东30°距离30米处,过了2秒后行驶了50米,此时小汽车与车速检测仪间的距离为40米. 问:2秒后小汽车在车速检测仪的哪个方向 这辆小汽车超速了吗
车速检测仪
小汽车
30米
30°
北
60°
解:小汽车在车速检测仪的南偏东60°方向或北偏西60°方向.
25米/秒=90千米/时>70千米/时
∴小汽车超速了.
2秒后
50米
40米
如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
分析:连接AC,把四边形分成两个三角形.先用勾股定理求出AC的长度,再利用勾股定理的逆定理判断△ACD是直角三角形.
A
D
B
C
3
4
13
12
解:连接AC.
在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,
且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
A
D
B
C
3
4
13
12
如图,在△ABC中,AB:BC:CA=3:4:5且周长为36cm,点P从点A开始沿AB边向B点以每秒2cm的速度移动,点Q从点C沿CB边向点B以每秒1cm的速度移动,如果同时出发,则过3s时,求PQ的长.
解:设AB为3xcm,BC为4xcm,AC为5xcm,∵周长为36cm,即AB+BC+AC=36cm,
∴AB=9cm,BC=12cm,AC=15cm.
∵AB2+BC2=AC2,∴△ABC是直角三角形,过3秒时,
BP=9-3×2=3(cm),BQ=12-1×3=9(cm),
在Rt△PBQ中,由勾股定理得
∴3x+4x+5x=36,
解得x=3.
P
C
B
A
Q
