人教版八年级下册第十八章平行四边形典型题型总结(63张ppt)
文档属性
| 名称 | 人教版八年级下册第十八章平行四边形典型题型总结(63张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 18:58:58 | ||
图片预览


文档简介
(共63张PPT)
平行四边形典型题型总结
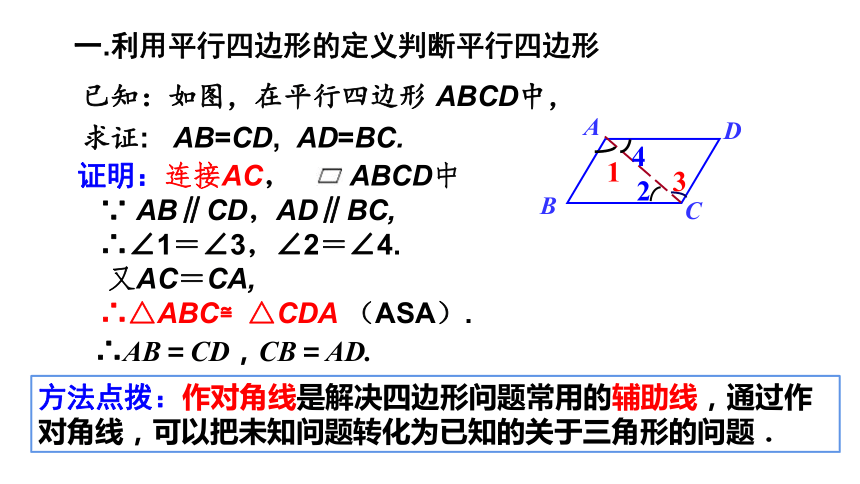
已知:如图,在平行四边形 ABCD中,
求证: AB=CD, AD=BC.
证明:连接AC, ABCD中
∵ AB∥CD,AD∥BC,
∴∠1=∠3,∠2=∠4.
又AC=CA,
∴△ABC≌△CDA (ASA).
∴AB=CD,CB=AD.
方法点拨:作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知问题转化为已知的关于三角形的问题.
A
D
C
B
1
4
2
3
一.利用平行四边形的定义判断平行四边形
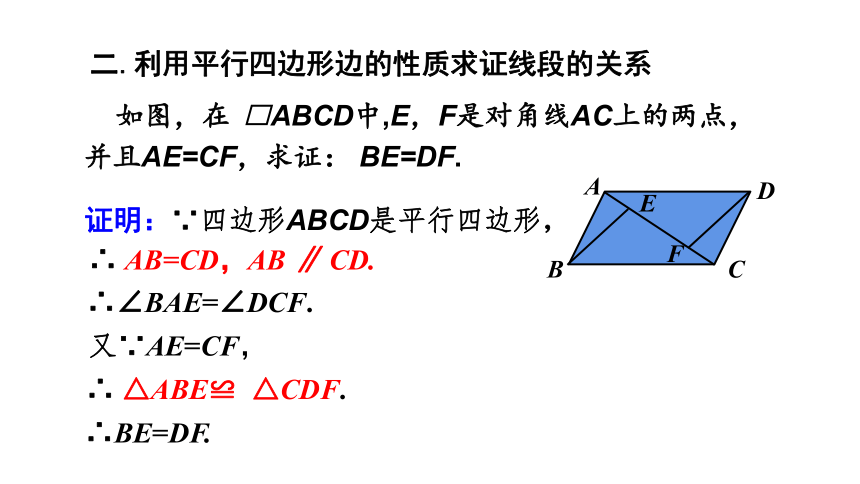
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF.
∴ AB=CD,AB ∥ CD.
又∵AE=CF,
∴BE=DF.
A
D
B
C
E
F
二.利用平行四边形边的性质求证线段的关系
如图,在 ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.
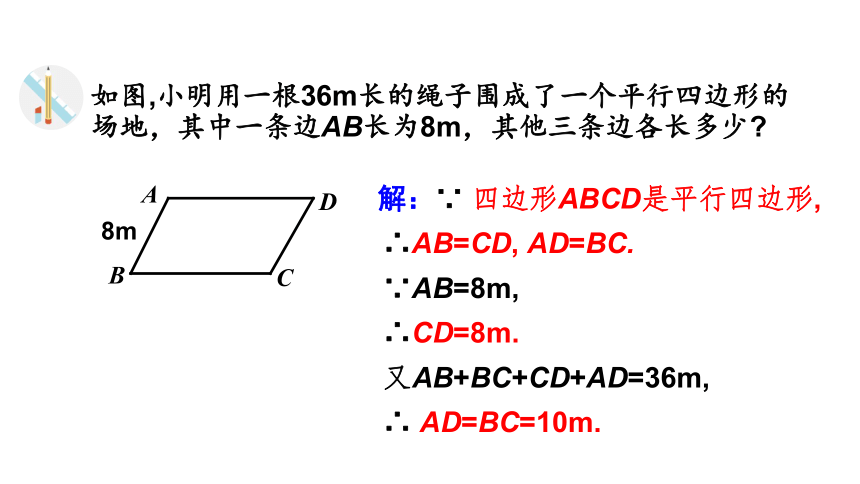
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少
解:∵ 四边形ABCD是平行四边形,
∴AB=CD, AD=BC.
∵AB=8m,
∴CD=8m.
又AB+BC+CD+AD=36m,
∴ AD=BC=10m.
A
D
B
C
8m
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD.
∴∠1=∠2,∠3=∠4.
又∵AC是△ABC和△CDA的公共边,
∴△ABC≌△CDA.
∴∠ABC=∠ADC.
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,
∴∠BAD=∠BCD.
A
B
C
D
1
4
3
2
已知:四边形ABCD是平行四边形.
求证:∠BAD=∠BCD,∠ABC=∠ADC.
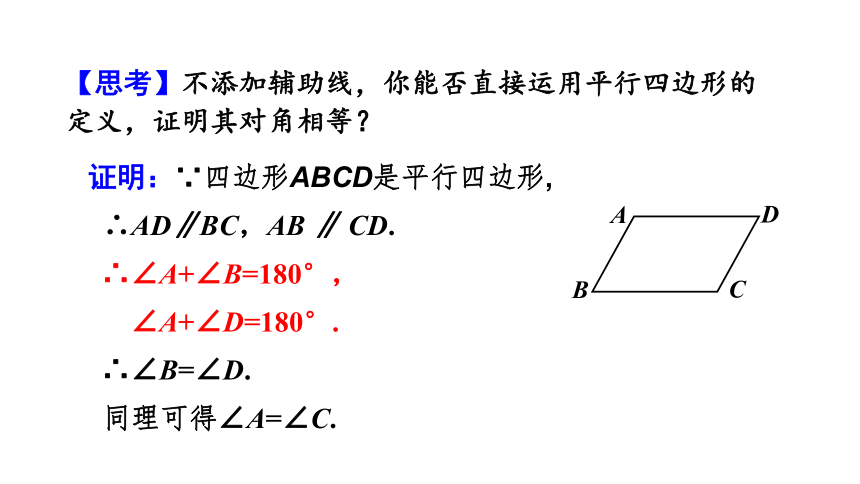
【思考】不添加辅助线,你能否直接运用平行四边形的
定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD.
∴∠A+∠B=180°,
∠A+∠D=180°.
∴∠B=∠D.
同理可得∠A=∠C.
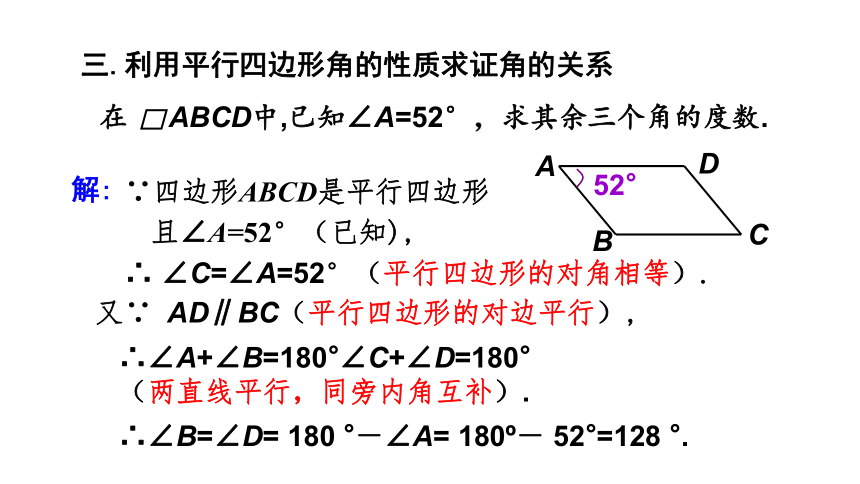
解:
∵四边形ABCD是平行四边形
且∠A=52°(已知),
∴ ∠C=∠A=52°(平行四边形的对角相等).
又∵ AD∥BC(平行四边形的对边平行),
∴∠A+∠B=180°∠C+∠D=180°
(两直线平行,同旁内角互补).
∴∠B=∠D= 180 °-∠A= 180 - 52°=128 °.
A
B
C
D
52°
三.利用平行四边形角的性质求证角的关系
在 ABCD中,已知∠A=52°,求其余三个角的度数.
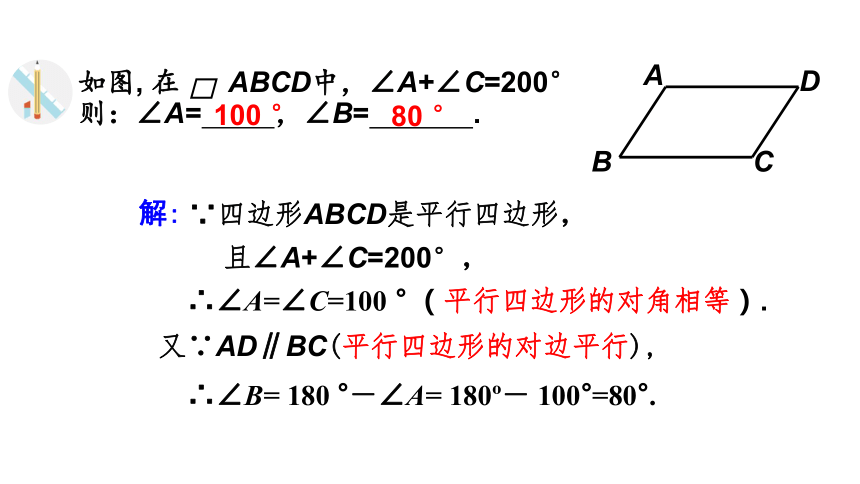
A
D
B
C
100 °
80 °
解:
∴∠B= 180 °-∠A= 180 - 100°=80°.
又∵AD∥BC(平行四边形的对边平行),
∵四边形ABCD是平行四边形,
∴∠A=∠C=100 ° (平行四边形的对角相等).
且∠A+∠C=200°,
如图, 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
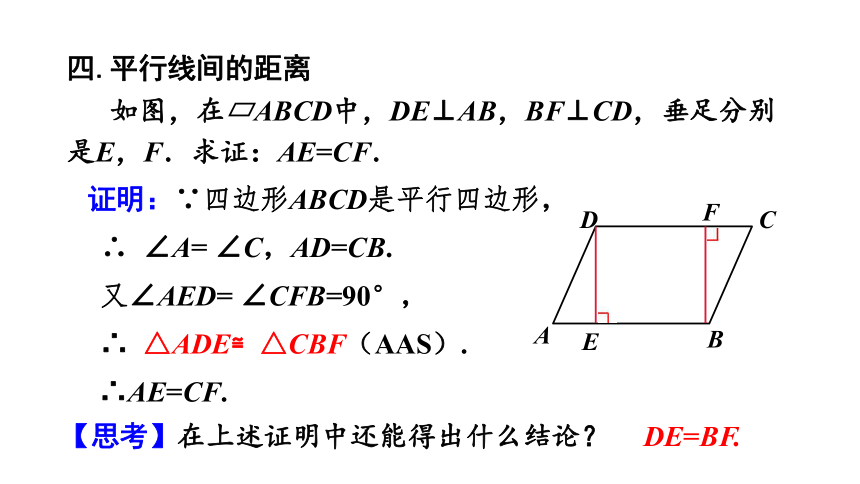
如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴ ∠A= ∠C,AD=CB.
又∠AED= ∠CFB=90°,
∴ △ADE≌△CBF(AAS).
∴AE=CF.
【思考】在上述证明中还能得出什么结论?
D
A
B
C
F
E
DE=BF.
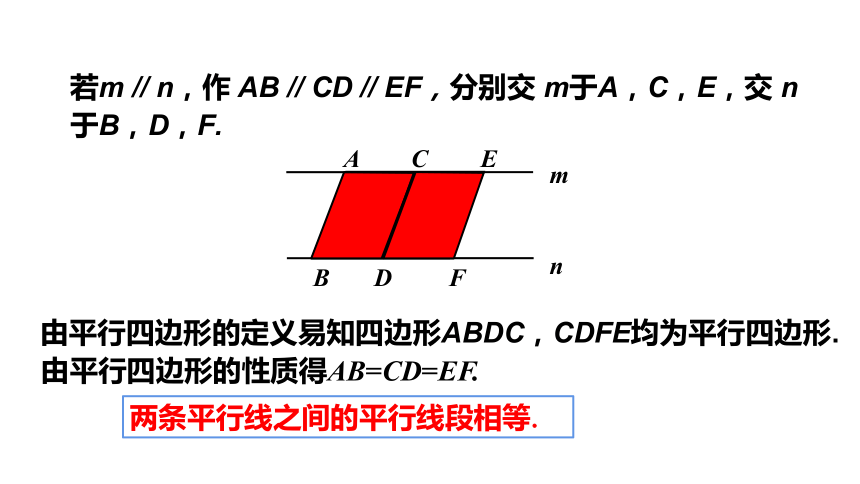
四.平行线间的距离
C
B
F
E
A
D
若m // n,作 AB // CD // EF,分别交 m于A,C,E,交 n于B,D,F.
由平行四边形的性质得AB=CD=EF.
两条平行线之间的平行线段相等.
m
n
由平行四边形的定义易知四边形ABDC,CDFE均为平行四边形.
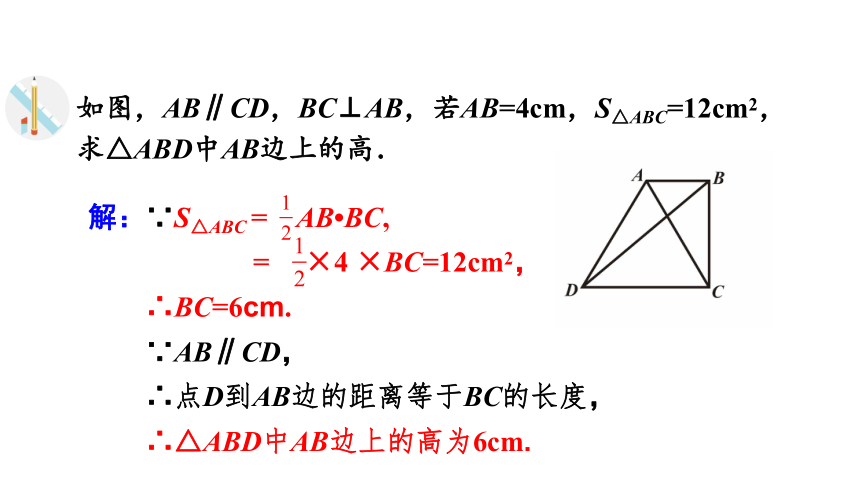
如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,
求△ABD中AB边上的高.
解:∵S△ABC = AB BC,
= ×4 ×BC=12cm2,
∴BC=6cm.
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴△ABD中AB边上的高为6cm.
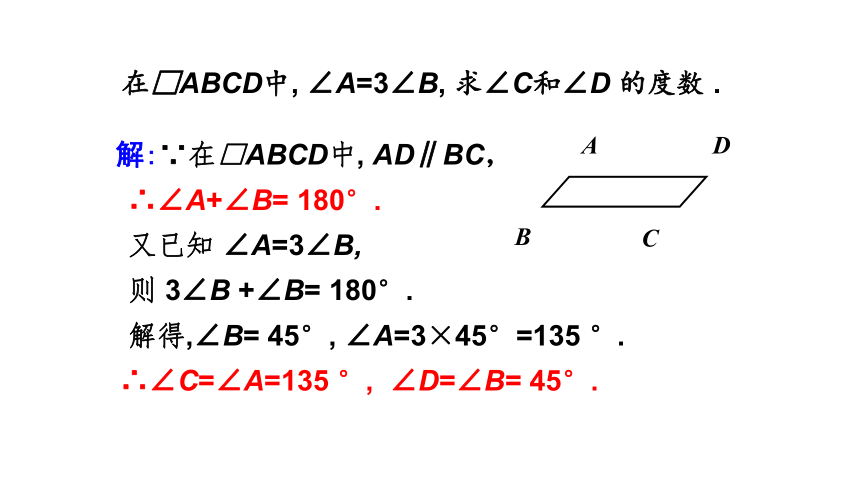
在□ABCD中, ∠A=3∠B, 求∠C和∠D 的度数 .
B
C
A
D
解:∵在□ABCD中, AD∥BC,
∴∠A+∠B= 180°.
又已知 ∠A=3∠B,
则 3∠B +∠B= 180°.
解得,∠B= 45°, ∠A=3×45°=135 °.
∴∠C=∠A=135 °, ∠D=∠B= 45°.
如图,小明用一根48m长的绳子围成了一个平行四边形的场地,其中一条边AB长为10m,其他三条边各长多少
解:∵ 四边形ABCD是平行四边形,
∴AB=CD, AD=BC.
∵AB=10m,
∴CD=10m.
又AB+BC+CD+AD=48,
∴ AD=BC=14m.
A
D
B
C
10m
有一块形状如图所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC , AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,
AD=BC=80cm.
∴ED=AD-AE=20cm.
答:DE的长度是20cm, ∠D的度数是60°.
证明:∵ 四边形BEFM是平行四边形,
∴BM=EF,AB//EF.
∵ AD平分∠BAC,∴∠BAD=∠CAD.
∵AB//EF, ∴ ∠BAD=∠AEF,
∴∠CAD =∠AEF, ∴ AF=EF,
∴ AF=BM.
如图,在△ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形.求证:AF=BM.
B
D
C
E
F
A
M
如图,在 ABCD中,连接AC,BD,并设它们相交于点O.OA与OC,OB与OD有什么关系?
D
A
B
C
O
猜想:平行四边形的对角线互相平分.
想一想,平行四边形除了边、角这两个要素的性质外,对角线有什么性质?
五.平行四边形对角线的性质
你能证明这个猜想吗?
如图,在 ABCD中,对角线AC,BD 相交于点O,
OA与OC,OB与OD有什么关系?
求证:OA=OC,OB=OD.
证明:∵四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD.
∴ ∠1=∠2,∠3=∠4.
∴ △COD≌△AOB.
∴ OA=OC,OB=OD.
D
A
B
C
O
1
2
3
4
证明过程
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5cm,∴AB-AD=5cm.
又∵ ABCD的周长为60cm,∴AB+AD=30cm.
则AB=CD=17.5cm,AD=BC=12.5cm.
已知 ABCD的周长为60cm,对角线AC , BD相交于点O,△AOB的周长比△DOA的周长长5cm,求这个平行四边形各边的长.
六.利用平行四边形对角线的性质求线段的值
提示:平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.
C
B
A
D
O
如图,□ ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F. 求证:OE=OF.
七.利用平行四边形对角线的性质求线段的相等
B
C
D
A
O
F
E
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,OA=OC (平行四边形的性质).
∴∠EAO=∠FCO(两直线平行,内错角相等).
在△AOE和△COF中
∠AOE = ∠ COF﹙对顶角相等﹚,
OA = OC,
∠EAO = ∠FCO,
∴ △AOE≌△COF ( ASA ).
∴ OE = OF (全等三角形的对应边相等).
改变直线EF的位置,OE=OF还成立吗
如图,平行四边形ABCD中,AC , BD交于O点,点E , F分别是AO , CO的中点,试判断线段BE , DF的数量关系并证明你的结论.
解:BE=DF,BE∥DF. 理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵点E , F分别是AO , CO的中点 ∴OE=OF.
在△OFD和△OEB中,
OE=OF,∠DOF=∠BOE,OD=OB,
∴△OFD≌△OEB.
∴BE=DF. ∠DFO=∠BEO.
∴ BE∥DF.
解:∵四边形ABCD是平行四边形,
根据勾股定理得 .
∴BC=AD=8cm,CD=AB=10cm.
∴△ABC是直角三角形.
又∵OA=OC,
如图,在 ABCD中,AB=10cm,AD=8cm,AC⊥BC. 求BC,CD,AC,OA的长,以及 ABCD的面积.
八.平行四边形的面积
∵AC⊥BC,
A
B
C
D
O
∴ .
如图,EF过 ABCD的对角线AC , BD的交点O,△AOE与△COF的面积有何关系?四边形AEFD与四边形BCFE的面积有何关系?
F
E
C
B
O
D
●
A
九.平行四边形中有关图形的面积
解:相等.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵△ADO与△ODC等底同高,
∴S△ADO=S△ODC.
同理可得S△ADO=S△ODC=S△BCO=S△AOB.
总结:平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
还可结合全等来证哟.
B
O
D
A
C
A
B
C
D
O
F
E
如图,AC,BD交于点O,EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗?
M
N
解:设直线EF交AD,BC于点N,M.
∵AD∥BC,
∴∠NAO=∠MCO,∠ANO=∠CMO.
又∵AO=CO,
∴△NAO≌△MCO,
∴S四边形ANMB=S△NAO+S△AOB+S△MOB=S△MCO+S△AOB+S△MOB
=S△AOB+S△COB= .
∴S四边形ANMB=S四边形CMND,
即平行四边形ABCD被EF所分的两个四边形面积相等.
十.利用平行四边形的有关图形的面积证明相等
把一个平行四边形分成3个三角形,已知两个阴影三角形的面积分别是9cm2和12cm2,求平行四边形的面积.
解:(9+12)×2
=21×2
=42(cm2)
答:平行四边形的面积是42cm2.
如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.
解:设AB=x,则BC=24-x.
根据平行四边形的面积公式可得,5x=10(24-x),
解得x=16.
则平行四边形ABCD的面积为5×16=80.
如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长是多少?
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD.
∵OE⊥BD,∴BE=DE.
∵△CDE的周长为10,∴DE+CE+CD=BE+CE+CD=BC+CD=10.
∴平行四边形ABCD的周长为2×(BC+CD)=20.
已知: 四边形ABCD中,AB=DC,AD=BC.
求证: 四边形ABCD是平行四边形.
A
B
C
D
连接AC,
在△ABC和△CDA中,
AB=CD (已知),
BC=DA(已知),
AC=CA (公共边),
∴△ABC≌△CDA(SSS).
∴ ∠1=∠4 , ∠ 2=∠3.
∴AB∥ CD , AD∥ BC.
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
你能用平行四边形的定义来证明吗?
如图,在Rt△MON中,∠MON=90°.求证:
四边形PONM是平行四边形.
证明:在Rt△MON中,
由勾股定理得(x-5)2+42=(x-3)2,
解得x=8.
∴PM=11-x=3,ON=x-5=3,MN=x-3=5.
∴PM=ON,OP=MN,
∴四边形PONM是平行四边形.
十一.利用两组对边分别相等识别平行四边形
如图, AD⊥AC,BC⊥AC,且AB=CD,
求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△CDA中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL).
∴BC=DA.
又∵AB=CD,
∴四边形ABCD是平行四边形.
已知:四边形ABCD, ∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
证明:
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
同理可证AB∥CD.
又∵∠A+ ∠B+ ∠C+ ∠D =360 °,
∴ 2∠A+ 2∠B=360 °,
∵∠A=∠C,∠B=∠D(已知),
即∠A+ ∠B=180 °.
∴ AD∥BC (同旁内角互补,两直线平行).
A
B
C
D
如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°;
(2)证明:∵AB∥DC,∴∠2=∠CAB.
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,又∵∠D=∠B=55°,
十二.利用平行四边形的判定定理2判定平行四边形
∴∠DCB=∠DAB=125°.
∴四边形ABCD是平行四边形.
已知:如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD.
∴△ADO ≌△CBO.
OA=OC,
证明:
OB=OD,
∠AOD=∠COB,
∴四边形ABCD是平行四边形.
求证:四边形ABCD是平行四边形.
A
C
D
B
O
2
1
在△ADO 和△CBO中,
∴ ∠1=∠2.
∴AD∥BC.
同理AB∥CD.
如图, □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
B
O
D
A
C
E
F
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
十三.利用平行四边形的判定定理3判定平行四边形
平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.
已知:如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
证明:连接AC,如图所示:
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS).
∴∠BAC=∠DCA,∠ACB=∠CAD.
∴AB∥CD,BC∥AD.
∴四边形ABCD是平行四边形.
B
D
A
C
如图,AC∥DE且AC=DE,AD,CE交于点B,AF,DG分别是△ABC,△BDE的中线,求证:四边形AGDF是平行四边形.
∵AC∥DE,AC=DE,
∴∠C=∠E,∠CAB=∠EDB.
∴△ABC≌△DBE.
∴AB=DB,CB=EB.
∵AF,DG分别是△ABC,△BDE的中线,
∴BG=BF.
∴四边形AGDF是平行四边形.
证明:
如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
在平行四边形ABCD中,∠A=∠C,AD=BC,
又∵BF=DH,∴AH=CF.
又∵AE=CG,
∴△AEH≌△CGF(SAS).
∴EH=GF.同理得△BEF≌△DGH(SAS).
∴GH=EF.
∴四边形EFGH是平行四边形.
证明:
如图,五边形ABCDE是正五边形,连接BD , CE,交于点P.
求证:四边形ABPE是平行四边形.
证明:∵五边形ABCDE是正五边形,
∴正五边形的每个内角的度数是
AB=BC=CD=DE=AE.
∴∠DEC=∠DCE= ×(180°-108°)=36°,
同理∠CBD=∠CDB=36°,∴∠ABP=∠AEP=108°-36°=72°.
∴∠BPE=360°-108°-72°-72°=108°=∠A.
∴四边形ABPE是平行四边形.
A
B
C
D
E
P
如图,在△ABC中,分别以AB,AC,BC为边在BC的同侧作等边△ABD、等边△ACE、等边△BCF.试说明四边形DAEF是平行四边形.
证明:∵△ABD和△BCF都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°.
∴∠DBF=∠ABC.又∵BD=BA,BF=BC,
∴△DBF≌△ABC(SAS).∴AC=DF.
又∵△ACE是等边三角形,∴AC=DF=AE.
同理可证△ABC≌△EFC,∴AB=EF=AD.
∴四边形DAEF是平行四边形.
∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
十四.直接利用平行四边形的判定定理4判定平行四边形
证明:
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥ EF,AD=EF,
EF∥ BC, EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.
四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
∵AB=CD,∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=DB ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS).
∴CE=BF,∠ACE=∠DBF.
∴CE∥BF.
∴四边形BFCE是平行四边形.
十五.平行四边形的判定定理4和全等三角形判定平行四边形
证明:
如图,点C是AB的中点,AD=CE,CD=BE.
(1)求证:△ACD≌△CBE.
(2)求证:四边形CBED是平行四边形.
证明:(1)∵点C是AB的中点,∴AC=BC.
在△ADC与△CEB中,
AD=CE , CD=BE , AC=CB ,
∴△ADC≌△CEB(SSS).
(2)∵△ADC≌△CEB,∴∠ACD=∠CBE.
∴CD∥BE.又∵CD=BE,∴四边形CBED是平行四边形.
如图,△ABC中,BD平分∠ABC,DF∥BC,EF∥AC,试问BF与CE相等吗?为什么?
十六.平行四边形的性质和判定的综合题目
解:BF=CE.理由如下:
∵DF∥BC,EF∥AC,
∴四边形FECD是平行四边形,∠FDB=∠DBE.
∴FD=CE.
∵BD平分∠ABC,∴∠FBD=∠EBD.
∴∠FBD=∠FDB.
∴BF=FD.
∴BF=CE.
如图,在 ABCD中,E,F分别是AB,CD的中点,连接DE,EF,BF,写出图中除 ABCD以外的所有的平行四边形.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵E,F分别是AB,CD的中点,
∴AE=EB=DF=FC.
∴四边形ADFE是平行四边形,
四边形EFCB是平行四边形,
四边形BEDF是平行四边形.
如图,在四边形ABCD中,AD∥BC,延长BC到E,使CE=BC,连接AE交CD于点F,点F是CD的中点.
求证:(1)△ADF≌△ECF;
(2)四边形ABCD是平行四边形.
证明:(1)∵AD∥BC,∴∠DAF=∠E,
∵点F是CD的中点,
∴DF=CF,在△ADF与△ECF中,
∴△ADF≌△ECF(AAS);
(2)∵△ADF≌△ECF,∴AD=EC.
∵CE=BC,∴AD=BC.
∵AD∥BC,∴四边形ABCD是平行四边形.
∠DAF= ∠E ,
DF=CF,
∠AFD= ∠EFC ,
如图,点E,C在线段BF上,BE=CF,∠B=∠DEF,∠ACB=∠F,求证:四边形ABED为平行四边形.
∵BE=CF,
∴BE+EC=CF+EC.即BC=EF.
又∵∠B=∠DEF,∠ACB=∠F,
∴△ABC≌△DEF.∴AB=DE.
∵∠B=∠DEF,∴AB∥DE.
∴四边形ABED是平行四边形.
证明:
如图,将 ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.求证:四边形BCED′是平行四边形.
由题意,得∠DAE=∠D′AE,∠DEA=∠D′EA, ∠D=∠AD′E,
∵DE∥AD′,∴∠DEA=∠EAD′.
∴∠DAE=∠EAD′=∠DEA=∠D′EA.
∴∠DAD′=∠DED′.
∴四边形DAD′E是平行四边形.
∴DE=AD′.
证明:
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.∴CE∥D′B,CE=D′B.
∴四边形BCED′是平行四边形.
如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_____; DP=________;
BQ=________;CQ=________;
tcm
(12-t)cm
(15-2t)cm
2tcm
(2)当t为何值时,四边形APQB是平行四边形?
解:根据题意有AP=tcm,CQ=2tcm,
PD=(12-t)cm,BQ=(15-2t)cm.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15-2t,
解得t=5.
∴t=5时四边形APQB是平行四边形.
解:由PD=(12-t)cm,CQ=2tcm,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即12-t=2t,解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
(3)当t为何值时,四边形PDCQ是平行四边形?
延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F,
连接FC.
∵∠AED=∠CEF,AE=CE,
证法1:
AD=CF.
∴BD CF.
又∵ ,
∴DF BC .
∴ DE∥BC, .
∴CF AD ,
证明:
B
C
A
D
E
如图,在△ABC中,点D,E分别是AB,AC边的中点,求证:
证明:
D
E
延长DE到F,使EF=DE.
连接AF , CF , DC .
∵AE=EC,DE=EF ,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形.
∴CF AD .
∴CF BD .
又∵ ,
∴DF BC .
∴ DE∥BC, .
B
C
A
证法2:
A
B
C
D
E
如图,D , E , F分别是△ABC的三边的中点,那么,DE , DF , EF都是△ABC的中位线.
F
DE∥BC且DE= BC;
同理:DF∥AC且DF= AC;
EF∥AB且EF= AB.
如图,在△ABC中,D,E分别为AC,BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长.
解:∵D,E分别为AC,BC的中点,
∴DE∥AB,∴∠2=∠3.
又∵AF平分∠CAB,
∴∠1=∠3.∴∠1=∠2.
∴AD=DF=3.
∴AC=2AD=2DF=6.
十七.利用中位线定理求线段
如图, A ,B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A,B两点的实际距离?根据是什么?
A
B
C
测出MN的长,就可知A,B两点的距离.
M
N
分别找出AC和BC的中点M,N.
若MN=36 m,则AB=
2MN=72 m.
如果,MN两点之间还有阻隔,你有什么解决办法?
如图,D,E分别是△ABC的边AB,AC的中点,点O是△ABC内部任意一点,连接OB,OC,点G,F分别是OB,OC的中点,顺次连接点D,G,F,E.求证:四边形DGFE是平行四边形.
A
B
C
G
F
E
D
O
∴四边形DGFE是平行四边形.
证明:
十八.利用三角形的中位线判断平行四边形
在△ABC中,∵AD=BD,AE=CE,
=
∴ .
=
∴ .
=
∴ .
在△OBC中,∵OG=BG,OF=CF,
已知: 如图,点E,F,G,H分别是四边形ABCD各边中点,
求证:四边形EFGH为平行四边形.
证明:连接AC.
∵ E , F是AB , BC边中点,
∴EF∥AC且EF= AC.
同理:HG ∥ AC且HG = AC.
∴EF ∥ HG且EF = HG.
∴四边形EFGH为平行四边形.
E
F
G
H
A
B
C
D
如图,在四边形ABCD中,AB=CD,M ,N , P分别是AD , BC,BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数.
解:∵M,N,P分别是AD,BC,BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线.
∴PM= AB,PN= DC,PM∥AB,PN∥DC.
∵AB=CD,∴PM=PN.∴△PMN是等腰三角形.
∵PM∥AB,PN∥DC,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°.
十九.利用三角形的中位线求角度
∴∠MPN=∠MPD+(180° ∠NPB)=130°.
∴∠PMN=(180° 130°)÷ 2 =25°.
如图, ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵ ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC.
∴△DOE的周长为OD+OE+DE= (BD+BC+CD)=15.
如图,在△ABC中,AB=AC,E为AB的中点,在AB的延长线上取一点D,使BD=AB,求证:CD=2CE.
证明:取AC的中点F,连接BF.
∵BD=AB,
∴BF为△ADC的中位线,∴DC=2BF.
∵E为AB的中点,AB=AC,
∴BE=CF,∠ABC=∠ACB.
∵BC=CB,∴△EBC≌△FCB.
∴CE=BF.
∴CD=2CE.
F
如图,E,F,G,H分别为四边形ABCD四边之中点.
求证:四边形EFGH为平行四边形.
证明:如图,连接BD.
∵E,F,G,H分别为四边形ABCD四边之中点,
∴EH是△ABD的中位线, FG是△BCD的中位线,
∴EH∥BD且EH= BD, FG∥BD且FG= BD.
∴EH∥FG且EH=FG ,
∴四边形EFGH为平行四边形.
G
如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.
解:取BC边的中点G,连接EG , FG.
∵E,F分别为AB,CD的中点,
∴EG是△ABC的中位线,FG是△BCD的中位线.
又BD=12,AC=16,AC⊥BD,
∴EG=8,FG=6,EG⊥FG.
∴
∴EG∥AC,
FG∥BD,
平行四边形典型题型总结
已知:如图,在平行四边形 ABCD中,
求证: AB=CD, AD=BC.
证明:连接AC, ABCD中
∵ AB∥CD,AD∥BC,
∴∠1=∠3,∠2=∠4.
又AC=CA,
∴△ABC≌△CDA (ASA).
∴AB=CD,CB=AD.
方法点拨:作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知问题转化为已知的关于三角形的问题.
A
D
C
B
1
4
2
3
一.利用平行四边形的定义判断平行四边形
证明:∵四边形ABCD是平行四边形,
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF.
∴ AB=CD,AB ∥ CD.
又∵AE=CF,
∴BE=DF.
A
D
B
C
E
F
二.利用平行四边形边的性质求证线段的关系
如图,在 ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少
解:∵ 四边形ABCD是平行四边形,
∴AB=CD, AD=BC.
∵AB=8m,
∴CD=8m.
又AB+BC+CD+AD=36m,
∴ AD=BC=10m.
A
D
B
C
8m
证明:如图,连接AC.
∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD.
∴∠1=∠2,∠3=∠4.
又∵AC是△ABC和△CDA的公共边,
∴△ABC≌△CDA.
∴∠ABC=∠ADC.
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,
∴∠BAD=∠BCD.
A
B
C
D
1
4
3
2
已知:四边形ABCD是平行四边形.
求证:∠BAD=∠BCD,∠ABC=∠ADC.
【思考】不添加辅助线,你能否直接运用平行四边形的
定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD.
∴∠A+∠B=180°,
∠A+∠D=180°.
∴∠B=∠D.
同理可得∠A=∠C.
解:
∵四边形ABCD是平行四边形
且∠A=52°(已知),
∴ ∠C=∠A=52°(平行四边形的对角相等).
又∵ AD∥BC(平行四边形的对边平行),
∴∠A+∠B=180°∠C+∠D=180°
(两直线平行,同旁内角互补).
∴∠B=∠D= 180 °-∠A= 180 - 52°=128 °.
A
B
C
D
52°
三.利用平行四边形角的性质求证角的关系
在 ABCD中,已知∠A=52°,求其余三个角的度数.
A
D
B
C
100 °
80 °
解:
∴∠B= 180 °-∠A= 180 - 100°=80°.
又∵AD∥BC(平行四边形的对边平行),
∵四边形ABCD是平行四边形,
∴∠A=∠C=100 ° (平行四边形的对角相等).
且∠A+∠C=200°,
如图, 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴ ∠A= ∠C,AD=CB.
又∠AED= ∠CFB=90°,
∴ △ADE≌△CBF(AAS).
∴AE=CF.
【思考】在上述证明中还能得出什么结论?
D
A
B
C
F
E
DE=BF.
四.平行线间的距离
C
B
F
E
A
D
若m // n,作 AB // CD // EF,分别交 m于A,C,E,交 n于B,D,F.
由平行四边形的性质得AB=CD=EF.
两条平行线之间的平行线段相等.
m
n
由平行四边形的定义易知四边形ABDC,CDFE均为平行四边形.
如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,
求△ABD中AB边上的高.
解:∵S△ABC = AB BC,
= ×4 ×BC=12cm2,
∴BC=6cm.
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴△ABD中AB边上的高为6cm.
在□ABCD中, ∠A=3∠B, 求∠C和∠D 的度数 .
B
C
A
D
解:∵在□ABCD中, AD∥BC,
∴∠A+∠B= 180°.
又已知 ∠A=3∠B,
则 3∠B +∠B= 180°.
解得,∠B= 45°, ∠A=3×45°=135 °.
∴∠C=∠A=135 °, ∠D=∠B= 45°.
如图,小明用一根48m长的绳子围成了一个平行四边形的场地,其中一条边AB长为10m,其他三条边各长多少
解:∵ 四边形ABCD是平行四边形,
∴AB=CD, AD=BC.
∵AB=10m,
∴CD=10m.
又AB+BC+CD+AD=48,
∴ AD=BC=14m.
A
D
B
C
10m
有一块形状如图所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC , AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,
AD=BC=80cm.
∴ED=AD-AE=20cm.
答:DE的长度是20cm, ∠D的度数是60°.
证明:∵ 四边形BEFM是平行四边形,
∴BM=EF,AB//EF.
∵ AD平分∠BAC,∴∠BAD=∠CAD.
∵AB//EF, ∴ ∠BAD=∠AEF,
∴∠CAD =∠AEF, ∴ AF=EF,
∴ AF=BM.
如图,在△ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形.求证:AF=BM.
B
D
C
E
F
A
M
如图,在 ABCD中,连接AC,BD,并设它们相交于点O.OA与OC,OB与OD有什么关系?
D
A
B
C
O
猜想:平行四边形的对角线互相平分.
想一想,平行四边形除了边、角这两个要素的性质外,对角线有什么性质?
五.平行四边形对角线的性质
你能证明这个猜想吗?
如图,在 ABCD中,对角线AC,BD 相交于点O,
OA与OC,OB与OD有什么关系?
求证:OA=OC,OB=OD.
证明:∵四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD.
∴ ∠1=∠2,∠3=∠4.
∴ △COD≌△AOB.
∴ OA=OC,OB=OD.
D
A
B
C
O
1
2
3
4
证明过程
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5cm,∴AB-AD=5cm.
又∵ ABCD的周长为60cm,∴AB+AD=30cm.
则AB=CD=17.5cm,AD=BC=12.5cm.
已知 ABCD的周长为60cm,对角线AC , BD相交于点O,△AOB的周长比△DOA的周长长5cm,求这个平行四边形各边的长.
六.利用平行四边形对角线的性质求线段的值
提示:平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.
C
B
A
D
O
如图,□ ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F. 求证:OE=OF.
七.利用平行四边形对角线的性质求线段的相等
B
C
D
A
O
F
E
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,OA=OC (平行四边形的性质).
∴∠EAO=∠FCO(两直线平行,内错角相等).
在△AOE和△COF中
∠AOE = ∠ COF﹙对顶角相等﹚,
OA = OC,
∠EAO = ∠FCO,
∴ △AOE≌△COF ( ASA ).
∴ OE = OF (全等三角形的对应边相等).
改变直线EF的位置,OE=OF还成立吗
如图,平行四边形ABCD中,AC , BD交于O点,点E , F分别是AO , CO的中点,试判断线段BE , DF的数量关系并证明你的结论.
解:BE=DF,BE∥DF. 理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵点E , F分别是AO , CO的中点 ∴OE=OF.
在△OFD和△OEB中,
OE=OF,∠DOF=∠BOE,OD=OB,
∴△OFD≌△OEB.
∴BE=DF. ∠DFO=∠BEO.
∴ BE∥DF.
解:∵四边形ABCD是平行四边形,
根据勾股定理得 .
∴BC=AD=8cm,CD=AB=10cm.
∴△ABC是直角三角形.
又∵OA=OC,
如图,在 ABCD中,AB=10cm,AD=8cm,AC⊥BC. 求BC,CD,AC,OA的长,以及 ABCD的面积.
八.平行四边形的面积
∵AC⊥BC,
A
B
C
D
O
∴ .
如图,EF过 ABCD的对角线AC , BD的交点O,△AOE与△COF的面积有何关系?四边形AEFD与四边形BCFE的面积有何关系?
F
E
C
B
O
D
●
A
九.平行四边形中有关图形的面积
解:相等.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵△ADO与△ODC等底同高,
∴S△ADO=S△ODC.
同理可得S△ADO=S△ODC=S△BCO=S△AOB.
总结:平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
还可结合全等来证哟.
B
O
D
A
C
A
B
C
D
O
F
E
如图,AC,BD交于点O,EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗?
M
N
解:设直线EF交AD,BC于点N,M.
∵AD∥BC,
∴∠NAO=∠MCO,∠ANO=∠CMO.
又∵AO=CO,
∴△NAO≌△MCO,
∴S四边形ANMB=S△NAO+S△AOB+S△MOB=S△MCO+S△AOB+S△MOB
=S△AOB+S△COB= .
∴S四边形ANMB=S四边形CMND,
即平行四边形ABCD被EF所分的两个四边形面积相等.
十.利用平行四边形的有关图形的面积证明相等
把一个平行四边形分成3个三角形,已知两个阴影三角形的面积分别是9cm2和12cm2,求平行四边形的面积.
解:(9+12)×2
=21×2
=42(cm2)
答:平行四边形的面积是42cm2.
如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.
解:设AB=x,则BC=24-x.
根据平行四边形的面积公式可得,5x=10(24-x),
解得x=16.
则平行四边形ABCD的面积为5×16=80.
如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长是多少?
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD.
∵OE⊥BD,∴BE=DE.
∵△CDE的周长为10,∴DE+CE+CD=BE+CE+CD=BC+CD=10.
∴平行四边形ABCD的周长为2×(BC+CD)=20.
已知: 四边形ABCD中,AB=DC,AD=BC.
求证: 四边形ABCD是平行四边形.
A
B
C
D
连接AC,
在△ABC和△CDA中,
AB=CD (已知),
BC=DA(已知),
AC=CA (公共边),
∴△ABC≌△CDA(SSS).
∴ ∠1=∠4 , ∠ 2=∠3.
∴AB∥ CD , AD∥ BC.
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
你能用平行四边形的定义来证明吗?
如图,在Rt△MON中,∠MON=90°.求证:
四边形PONM是平行四边形.
证明:在Rt△MON中,
由勾股定理得(x-5)2+42=(x-3)2,
解得x=8.
∴PM=11-x=3,ON=x-5=3,MN=x-3=5.
∴PM=ON,OP=MN,
∴四边形PONM是平行四边形.
十一.利用两组对边分别相等识别平行四边形
如图, AD⊥AC,BC⊥AC,且AB=CD,
求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△CDA中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL).
∴BC=DA.
又∵AB=CD,
∴四边形ABCD是平行四边形.
已知:四边形ABCD, ∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
证明:
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
同理可证AB∥CD.
又∵∠A+ ∠B+ ∠C+ ∠D =360 °,
∴ 2∠A+ 2∠B=360 °,
∵∠A=∠C,∠B=∠D(已知),
即∠A+ ∠B=180 °.
∴ AD∥BC (同旁内角互补,两直线平行).
A
B
C
D
如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°;
(2)证明:∵AB∥DC,∴∠2=∠CAB.
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,又∵∠D=∠B=55°,
十二.利用平行四边形的判定定理2判定平行四边形
∴∠DCB=∠DAB=125°.
∴四边形ABCD是平行四边形.
已知:如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD.
∴△ADO ≌△CBO.
OA=OC,
证明:
OB=OD,
∠AOD=∠COB,
∴四边形ABCD是平行四边形.
求证:四边形ABCD是平行四边形.
A
C
D
B
O
2
1
在△ADO 和△CBO中,
∴ ∠1=∠2.
∴AD∥BC.
同理AB∥CD.
如图, □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
B
O
D
A
C
E
F
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
十三.利用平行四边形的判定定理3判定平行四边形
平行四边形的其中一个判定定理是:两组对边分别相等的四边形是平行四边形.请你证明这个判定定理.
已知:如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
证明:连接AC,如图所示:
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS).
∴∠BAC=∠DCA,∠ACB=∠CAD.
∴AB∥CD,BC∥AD.
∴四边形ABCD是平行四边形.
B
D
A
C
如图,AC∥DE且AC=DE,AD,CE交于点B,AF,DG分别是△ABC,△BDE的中线,求证:四边形AGDF是平行四边形.
∵AC∥DE,AC=DE,
∴∠C=∠E,∠CAB=∠EDB.
∴△ABC≌△DBE.
∴AB=DB,CB=EB.
∵AF,DG分别是△ABC,△BDE的中线,
∴BG=BF.
∴四边形AGDF是平行四边形.
证明:
如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
在平行四边形ABCD中,∠A=∠C,AD=BC,
又∵BF=DH,∴AH=CF.
又∵AE=CG,
∴△AEH≌△CGF(SAS).
∴EH=GF.同理得△BEF≌△DGH(SAS).
∴GH=EF.
∴四边形EFGH是平行四边形.
证明:
如图,五边形ABCDE是正五边形,连接BD , CE,交于点P.
求证:四边形ABPE是平行四边形.
证明:∵五边形ABCDE是正五边形,
∴正五边形的每个内角的度数是
AB=BC=CD=DE=AE.
∴∠DEC=∠DCE= ×(180°-108°)=36°,
同理∠CBD=∠CDB=36°,∴∠ABP=∠AEP=108°-36°=72°.
∴∠BPE=360°-108°-72°-72°=108°=∠A.
∴四边形ABPE是平行四边形.
A
B
C
D
E
P
如图,在△ABC中,分别以AB,AC,BC为边在BC的同侧作等边△ABD、等边△ACE、等边△BCF.试说明四边形DAEF是平行四边形.
证明:∵△ABD和△BCF都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°.
∴∠DBF=∠ABC.又∵BD=BA,BF=BC,
∴△DBF≌△ABC(SAS).∴AC=DF.
又∵△ACE是等边三角形,∴AC=DF=AE.
同理可证△ABC≌△EFC,∴AB=EF=AD.
∴四边形DAEF是平行四边形.
∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
十四.直接利用平行四边形的判定定理4判定平行四边形
证明:
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥ EF,AD=EF,
EF∥ BC, EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.
四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
∵AB=CD,∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=DB ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS).
∴CE=BF,∠ACE=∠DBF.
∴CE∥BF.
∴四边形BFCE是平行四边形.
十五.平行四边形的判定定理4和全等三角形判定平行四边形
证明:
如图,点C是AB的中点,AD=CE,CD=BE.
(1)求证:△ACD≌△CBE.
(2)求证:四边形CBED是平行四边形.
证明:(1)∵点C是AB的中点,∴AC=BC.
在△ADC与△CEB中,
AD=CE , CD=BE , AC=CB ,
∴△ADC≌△CEB(SSS).
(2)∵△ADC≌△CEB,∴∠ACD=∠CBE.
∴CD∥BE.又∵CD=BE,∴四边形CBED是平行四边形.
如图,△ABC中,BD平分∠ABC,DF∥BC,EF∥AC,试问BF与CE相等吗?为什么?
十六.平行四边形的性质和判定的综合题目
解:BF=CE.理由如下:
∵DF∥BC,EF∥AC,
∴四边形FECD是平行四边形,∠FDB=∠DBE.
∴FD=CE.
∵BD平分∠ABC,∴∠FBD=∠EBD.
∴∠FBD=∠FDB.
∴BF=FD.
∴BF=CE.
如图,在 ABCD中,E,F分别是AB,CD的中点,连接DE,EF,BF,写出图中除 ABCD以外的所有的平行四边形.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵E,F分别是AB,CD的中点,
∴AE=EB=DF=FC.
∴四边形ADFE是平行四边形,
四边形EFCB是平行四边形,
四边形BEDF是平行四边形.
如图,在四边形ABCD中,AD∥BC,延长BC到E,使CE=BC,连接AE交CD于点F,点F是CD的中点.
求证:(1)△ADF≌△ECF;
(2)四边形ABCD是平行四边形.
证明:(1)∵AD∥BC,∴∠DAF=∠E,
∵点F是CD的中点,
∴DF=CF,在△ADF与△ECF中,
∴△ADF≌△ECF(AAS);
(2)∵△ADF≌△ECF,∴AD=EC.
∵CE=BC,∴AD=BC.
∵AD∥BC,∴四边形ABCD是平行四边形.
∠DAF= ∠E ,
DF=CF,
∠AFD= ∠EFC ,
如图,点E,C在线段BF上,BE=CF,∠B=∠DEF,∠ACB=∠F,求证:四边形ABED为平行四边形.
∵BE=CF,
∴BE+EC=CF+EC.即BC=EF.
又∵∠B=∠DEF,∠ACB=∠F,
∴△ABC≌△DEF.∴AB=DE.
∵∠B=∠DEF,∴AB∥DE.
∴四边形ABED是平行四边形.
证明:
如图,将 ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.求证:四边形BCED′是平行四边形.
由题意,得∠DAE=∠D′AE,∠DEA=∠D′EA, ∠D=∠AD′E,
∵DE∥AD′,∴∠DEA=∠EAD′.
∴∠DAE=∠EAD′=∠DEA=∠D′EA.
∴∠DAD′=∠DED′.
∴四边形DAD′E是平行四边形.
∴DE=AD′.
证明:
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.∴CE∥D′B,CE=D′B.
∴四边形BCED′是平行四边形.
如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_____; DP=________;
BQ=________;CQ=________;
tcm
(12-t)cm
(15-2t)cm
2tcm
(2)当t为何值时,四边形APQB是平行四边形?
解:根据题意有AP=tcm,CQ=2tcm,
PD=(12-t)cm,BQ=(15-2t)cm.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15-2t,
解得t=5.
∴t=5时四边形APQB是平行四边形.
解:由PD=(12-t)cm,CQ=2tcm,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即12-t=2t,解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
(3)当t为何值时,四边形PDCQ是平行四边形?
延长DE到F,使EF=DE.
F
∴四边形BCFD是平行四边形.
∴△ADE≌△CFE.
∴∠ADE=∠F,
连接FC.
∵∠AED=∠CEF,AE=CE,
证法1:
AD=CF.
∴BD CF.
又∵ ,
∴DF BC .
∴ DE∥BC, .
∴CF AD ,
证明:
B
C
A
D
E
如图,在△ABC中,点D,E分别是AB,AC边的中点,求证:
证明:
D
E
延长DE到F,使EF=DE.
连接AF , CF , DC .
∵AE=EC,DE=EF ,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形.
∴CF AD .
∴CF BD .
又∵ ,
∴DF BC .
∴ DE∥BC, .
B
C
A
证法2:
A
B
C
D
E
如图,D , E , F分别是△ABC的三边的中点,那么,DE , DF , EF都是△ABC的中位线.
F
DE∥BC且DE= BC;
同理:DF∥AC且DF= AC;
EF∥AB且EF= AB.
如图,在△ABC中,D,E分别为AC,BC的中点,AF平分∠CAB,交DE于点F.若DF=3,求AC的长.
解:∵D,E分别为AC,BC的中点,
∴DE∥AB,∴∠2=∠3.
又∵AF平分∠CAB,
∴∠1=∠3.∴∠1=∠2.
∴AD=DF=3.
∴AC=2AD=2DF=6.
十七.利用中位线定理求线段
如图, A ,B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A,B两点的实际距离?根据是什么?
A
B
C
测出MN的长,就可知A,B两点的距离.
M
N
分别找出AC和BC的中点M,N.
若MN=36 m,则AB=
2MN=72 m.
如果,MN两点之间还有阻隔,你有什么解决办法?
如图,D,E分别是△ABC的边AB,AC的中点,点O是△ABC内部任意一点,连接OB,OC,点G,F分别是OB,OC的中点,顺次连接点D,G,F,E.求证:四边形DGFE是平行四边形.
A
B
C
G
F
E
D
O
∴四边形DGFE是平行四边形.
证明:
十八.利用三角形的中位线判断平行四边形
在△ABC中,∵AD=BD,AE=CE,
=
∴ .
=
∴ .
=
∴ .
在△OBC中,∵OG=BG,OF=CF,
已知: 如图,点E,F,G,H分别是四边形ABCD各边中点,
求证:四边形EFGH为平行四边形.
证明:连接AC.
∵ E , F是AB , BC边中点,
∴EF∥AC且EF= AC.
同理:HG ∥ AC且HG = AC.
∴EF ∥ HG且EF = HG.
∴四边形EFGH为平行四边形.
E
F
G
H
A
B
C
D
如图,在四边形ABCD中,AB=CD,M ,N , P分别是AD , BC,BD的中点,∠ABD=20°,∠BDC=70°,求∠PMN的度数.
解:∵M,N,P分别是AD,BC,BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线.
∴PM= AB,PN= DC,PM∥AB,PN∥DC.
∵AB=CD,∴PM=PN.∴△PMN是等腰三角形.
∵PM∥AB,PN∥DC,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°.
十九.利用三角形的中位线求角度
∴∠MPN=∠MPD+(180° ∠NPB)=130°.
∴∠PMN=(180° 130°)÷ 2 =25°.
如图, ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
解:∵ ABCD的周长为36,
∴BC+CD=18.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE= CD,
∴OE= BC.
∴△DOE的周长为OD+OE+DE= (BD+BC+CD)=15.
如图,在△ABC中,AB=AC,E为AB的中点,在AB的延长线上取一点D,使BD=AB,求证:CD=2CE.
证明:取AC的中点F,连接BF.
∵BD=AB,
∴BF为△ADC的中位线,∴DC=2BF.
∵E为AB的中点,AB=AC,
∴BE=CF,∠ABC=∠ACB.
∵BC=CB,∴△EBC≌△FCB.
∴CE=BF.
∴CD=2CE.
F
如图,E,F,G,H分别为四边形ABCD四边之中点.
求证:四边形EFGH为平行四边形.
证明:如图,连接BD.
∵E,F,G,H分别为四边形ABCD四边之中点,
∴EH是△ABD的中位线, FG是△BCD的中位线,
∴EH∥BD且EH= BD, FG∥BD且FG= BD.
∴EH∥FG且EH=FG ,
∴四边形EFGH为平行四边形.
G
如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.
解:取BC边的中点G,连接EG , FG.
∵E,F分别为AB,CD的中点,
∴EG是△ABC的中位线,FG是△BCD的中位线.
又BD=12,AC=16,AC⊥BD,
∴EG=8,FG=6,EG⊥FG.
∴
∴EG∥AC,
FG∥BD,
