平面向量数量积
图片预览










文档简介
课件48张PPT。平面向量数量积
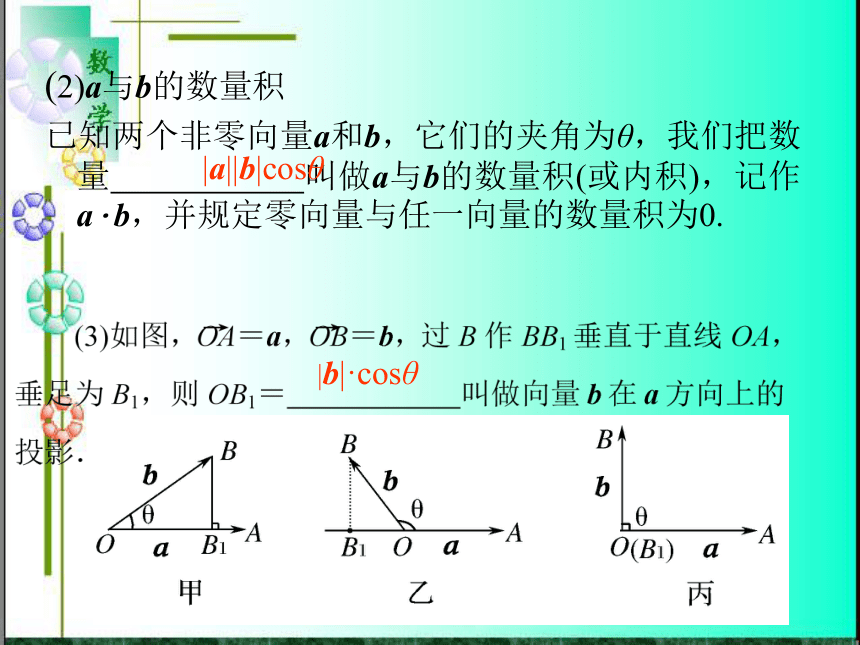
及应用? ? 1.理解平面向量数量积的含义及其物理意义.2.了解平面向量的数量积与向量投影的关系.3.掌握数量积的坐标表达式,会进行平面向量数量积的坐标运算.4.能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.5.会用向量方法解决某些简单的平面几何问题.(2)a与b的数量积
已知两个非零向量a和b,它们的夹角为θ,我们把数量 叫做a与b的数量积(或内积),记作a·b,并规定零向量与任一向量的数量积为0.|a||b|cosθ|b|·cosθ
当θ为锐角时,如图(甲),它是正值;
当θ为钝角时,如图(乙),它是负值;
当θ为直角时,如图(丙),它是0;
当θ为0°时,它是|b|;
当θ为180°时,它是-|b|.
(4)平面向量数量积的几何意义
数量积a·b等于a的长度|a|与b在a方向上的投影|b|cosθ的乘积.|a||b| -|a||b| 3.向量数量积的运算律
(1)a·b=b·a(交换律).
(2)(λa)·b=λ(a·b)=a·(λb).
(3)(a+b)·c=a·c+b·c.
4.平面向量数量积的坐标表示
(1)若a=(x1,y1),b=(x2,y2),则a·b= .
(2)设a=(x,y),则|a|= .
(3)若向量a的起点坐标和终点坐标分别为(x1,y1),(x2,y2),则|a|= ,
(4)设a=(x1,y1),b=(x2,y2),且a、b都是非零向量,则a⊥b?a·b=0? .x1x2+y1y2x1x2+y1y2=0二、平面向量的应用
用向量法证明几何问题的基本思想是:将问题中有关的线段表示为向量,然后根据图形的性质和特点,应用向量的运算性质、法则,推出所要求证的结论.要注意挖掘题目中,特别是几何图形中的隐含条件.5.平面向量与三角函数整合的题目,大多数本质仍是三角函数问题,只是同时兼顾平面向量的“共线”、“数量积”等基本概念与基本运算,解题时依据向量的有关概念与运算去掉向量外衣后,就是纯粹三角问题了.
6.平面向量与解析几何整合的题目,注意将题目中的条件和要解决的问题,通过“点”加以向量化,然后运用向量的运算来解决.误区警示
1.若a·b=0,a≠0不一定有b=0,因为当a⊥b时,总有a·b=0.
2.对于实数a、b、c,当b≠0时,若ab=bc,则a=c.但对于向量a,b,c,当b≠0时,由a·b=b·c却推不出a=c.因为由a·b=b·c得b·(a-c)=0,只要a-c与b垂直即可.
3.数量积不满足结合律,即对于向量a、b、c,(a·b)·c=a·(b·c)一般不成立,这是因为a·b与b·c都是实数.(a·b)·c与c共线,a·(b·c)与a共线,而c与a却未必共线.? 平面向量数量积的运算1.(密码改编)已知下列各式①a2=|a|2 ②? =? ③(a·b)2=a2·b2
④(a-b)2=a2-2a·b+b2⑤若a2=a·b,则a=b,其中正确的个数有?( ????)A.4个 B.3个 C.2个 D.1个解析:对②? =? ,而? 这种运算无意义,∴②错误.对③(a·b)2=|a|2|b|2cos2θ,而a2·b2=|a|2·|b|2,∴③错误,对⑤a2=a·b,∴a2-a·b=0,即a·(a-b)=0,得a⊥(a-b),不一定a=b.∴⑤错误.①④正确.考点一2.设e1,e2是两个单位向量,它们的夹角是60°,则(2e1-e2)·(-3e1+2e2)等于?(?????)A.-8 B.? C.-? D.8解析:由已知|e1|=|e2|=1,e1·e2=|e1||e2|cos60°=?.∴(2e1-e2)·(-3e1+2e2)=-6? +7e1·e2-2? =-8+? =-?.3.(2011·辽宁高考文,3)已知向量a=(2,1),b=(-1,k),a·(2a-b)=0,则k等于?( ????)A.-12 B.-6 C.6 D.12解析:由已知2a-b=(5,2-k),∴a·(2a-b)=12-k=0,
∴k=12.答案:D
[答案] D 两平面向量的夹角与垂直考点二1.求向量的夹角时要注意:数量积大于0说明不共线的两向量的夹角为锐角,数量积等于0说明两向量的夹角为直角,数量积小于0且两向量不共线时两向量的夹角就是钝角.2.当a,b是非坐标形式时,求a与b的夹角,需求得a·b及|a|,|b|或得出它们的关系.3.若已知a与b的坐标,则可直接利用公式4.注意函数思想与方程思想及数形结合思想的应用.平面向量的模1.平面向量a与b的夹角为60°,a=(2,0),|b|=1,则|a+2b|等于?( ????)考点三利用数量积求长度问题是数量积的重要应用,要掌握此类问题的处理方法:1.|a|2=a2=a·a;2.|a±b|2=(a±b)2=a2±2a·b+b2;3.若a=(x,y),则|a|=? .平面向量数量积的应用考点四练习
能力训练
及应用? ? 1.理解平面向量数量积的含义及其物理意义.2.了解平面向量的数量积与向量投影的关系.3.掌握数量积的坐标表达式,会进行平面向量数量积的坐标运算.4.能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.5.会用向量方法解决某些简单的平面几何问题.(2)a与b的数量积
已知两个非零向量a和b,它们的夹角为θ,我们把数量 叫做a与b的数量积(或内积),记作a·b,并规定零向量与任一向量的数量积为0.|a||b|cosθ|b|·cosθ
当θ为锐角时,如图(甲),它是正值;
当θ为钝角时,如图(乙),它是负值;
当θ为直角时,如图(丙),它是0;
当θ为0°时,它是|b|;
当θ为180°时,它是-|b|.
(4)平面向量数量积的几何意义
数量积a·b等于a的长度|a|与b在a方向上的投影|b|cosθ的乘积.|a||b| -|a||b| 3.向量数量积的运算律
(1)a·b=b·a(交换律).
(2)(λa)·b=λ(a·b)=a·(λb).
(3)(a+b)·c=a·c+b·c.
4.平面向量数量积的坐标表示
(1)若a=(x1,y1),b=(x2,y2),则a·b= .
(2)设a=(x,y),则|a|= .
(3)若向量a的起点坐标和终点坐标分别为(x1,y1),(x2,y2),则|a|= ,
(4)设a=(x1,y1),b=(x2,y2),且a、b都是非零向量,则a⊥b?a·b=0? .x1x2+y1y2x1x2+y1y2=0二、平面向量的应用
用向量法证明几何问题的基本思想是:将问题中有关的线段表示为向量,然后根据图形的性质和特点,应用向量的运算性质、法则,推出所要求证的结论.要注意挖掘题目中,特别是几何图形中的隐含条件.5.平面向量与三角函数整合的题目,大多数本质仍是三角函数问题,只是同时兼顾平面向量的“共线”、“数量积”等基本概念与基本运算,解题时依据向量的有关概念与运算去掉向量外衣后,就是纯粹三角问题了.
6.平面向量与解析几何整合的题目,注意将题目中的条件和要解决的问题,通过“点”加以向量化,然后运用向量的运算来解决.误区警示
1.若a·b=0,a≠0不一定有b=0,因为当a⊥b时,总有a·b=0.
2.对于实数a、b、c,当b≠0时,若ab=bc,则a=c.但对于向量a,b,c,当b≠0时,由a·b=b·c却推不出a=c.因为由a·b=b·c得b·(a-c)=0,只要a-c与b垂直即可.
3.数量积不满足结合律,即对于向量a、b、c,(a·b)·c=a·(b·c)一般不成立,这是因为a·b与b·c都是实数.(a·b)·c与c共线,a·(b·c)与a共线,而c与a却未必共线.? 平面向量数量积的运算1.(密码改编)已知下列各式①a2=|a|2 ②? =? ③(a·b)2=a2·b2
④(a-b)2=a2-2a·b+b2⑤若a2=a·b,则a=b,其中正确的个数有?( ????)A.4个 B.3个 C.2个 D.1个解析:对②? =? ,而? 这种运算无意义,∴②错误.对③(a·b)2=|a|2|b|2cos2θ,而a2·b2=|a|2·|b|2,∴③错误,对⑤a2=a·b,∴a2-a·b=0,即a·(a-b)=0,得a⊥(a-b),不一定a=b.∴⑤错误.①④正确.考点一2.设e1,e2是两个单位向量,它们的夹角是60°,则(2e1-e2)·(-3e1+2e2)等于?(?????)A.-8 B.? C.-? D.8解析:由已知|e1|=|e2|=1,e1·e2=|e1||e2|cos60°=?.∴(2e1-e2)·(-3e1+2e2)=-6? +7e1·e2-2? =-8+? =-?.3.(2011·辽宁高考文,3)已知向量a=(2,1),b=(-1,k),a·(2a-b)=0,则k等于?( ????)A.-12 B.-6 C.6 D.12解析:由已知2a-b=(5,2-k),∴a·(2a-b)=12-k=0,
∴k=12.答案:D
[答案] D 两平面向量的夹角与垂直考点二1.求向量的夹角时要注意:数量积大于0说明不共线的两向量的夹角为锐角,数量积等于0说明两向量的夹角为直角,数量积小于0且两向量不共线时两向量的夹角就是钝角.2.当a,b是非坐标形式时,求a与b的夹角,需求得a·b及|a|,|b|或得出它们的关系.3.若已知a与b的坐标,则可直接利用公式4.注意函数思想与方程思想及数形结合思想的应用.平面向量的模1.平面向量a与b的夹角为60°,a=(2,0),|b|=1,则|a+2b|等于?( ????)考点三利用数量积求长度问题是数量积的重要应用,要掌握此类问题的处理方法:1.|a|2=a2=a·a;2.|a±b|2=(a±b)2=a2±2a·b+b2;3.若a=(x,y),则|a|=? .平面向量数量积的应用考点四练习
能力训练
