解三角形的应用
图片预览




文档简介
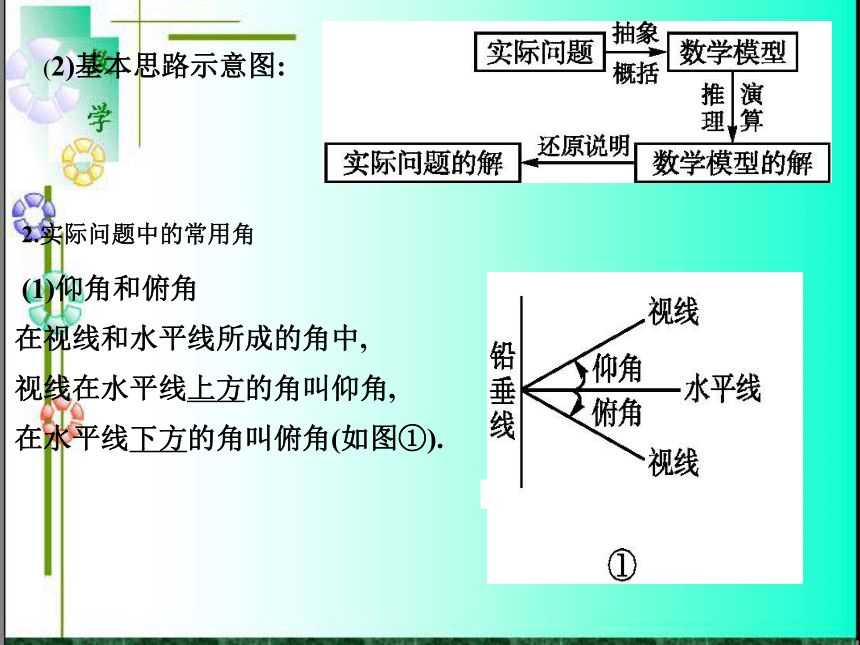
课件23张PPT。解三角形的应用解三角形的应用? ? 能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何问题有关的实际问题.? 1.应用正、余弦定理解斜三角形应用题的一般步骤及基本思路(1)一般步骤:①分析:理解题意,分清已知与未知,画出示意图;②建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学模型;③求解:利用正弦定理或余弦定理有序地解三角形,求得数学模型的解;④检验:检验上述所求的解是否具有实际意义,从而得出实际问题的解.(2)基本思路示意图:2.实际问题中的常用角(1)仰角和俯角在视线和水平线所成的角中,
视线在水平线上方的角叫仰角,
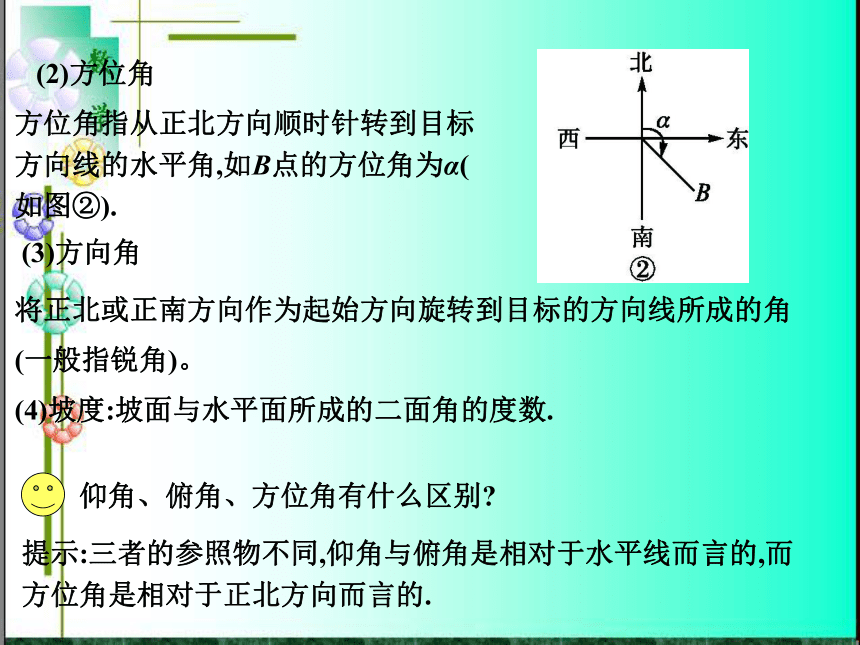
在水平线下方的角叫俯角(如图①).(2)方位角方位角指从正北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图②).(3)方向角将正北或正南方向作为起始方向旋转到目标的方向线所成的角
(一般指锐角)。(4)坡度:坡面与水平面所成的二面角的度数.仰角、俯角、方位角有什么区别?提示:三者的参照物不同,仰角与俯角是相对于水平线而言的,而方位角是相对于正北方向而言的.距离问题1.如图,设A、B两点在河的两岸,一测量者在A所在的河岸边选定一点C,在测出AC的距离为 50 m,∠ACB=45°,∠CAB=105°后,就可以计算出A、B两点的距离为?( ????)A.50? m B.50? mC.25? m D.? m解析:由题意知∠CBA=30°,由正弦定理得?
=? ,∴AB= = =50? m.答案:A考点一2.已知A、B两地的距离为10 km,B、C两地的距离为20 km,现测得∠ABC=120°,则A,C两地的距离为?( ????)A.10 km B.10? kmC.10? km D.10? km解析:由余弦定理得AC2=AB2+BC2-2AB·BC·cos∠ABC
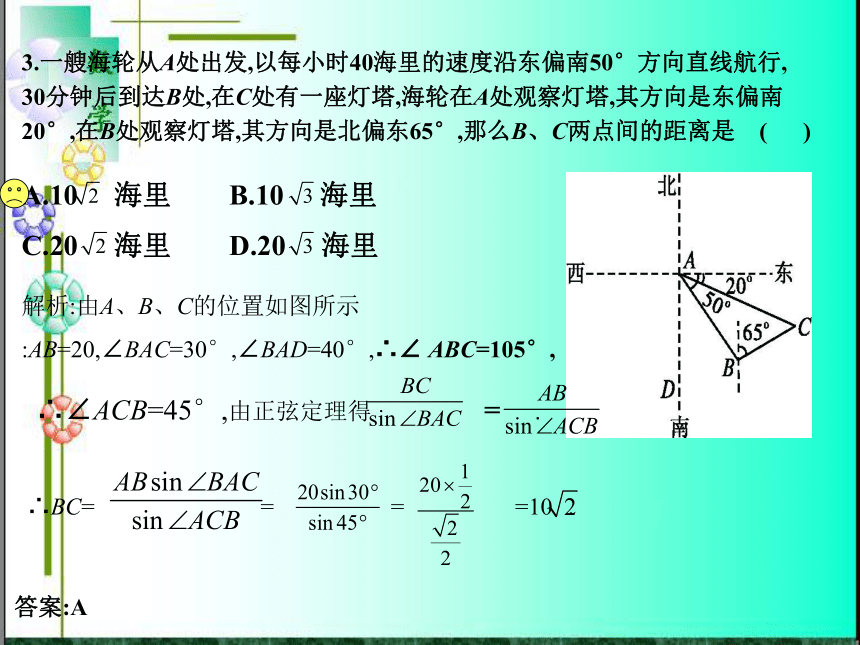
=100+400-2×10×20×(- )=700,∴AC=10?.答案:DABC10km20kmABC=120°,?3.一艘海轮从A处出发,以每小时40海里的速度沿东偏南50°方向直线航行, 30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南 20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是?(??????)A.10? 海里 B.10? 海里C.20? 海里 D.20? 海里解析:由A、B、C的位置如图所示
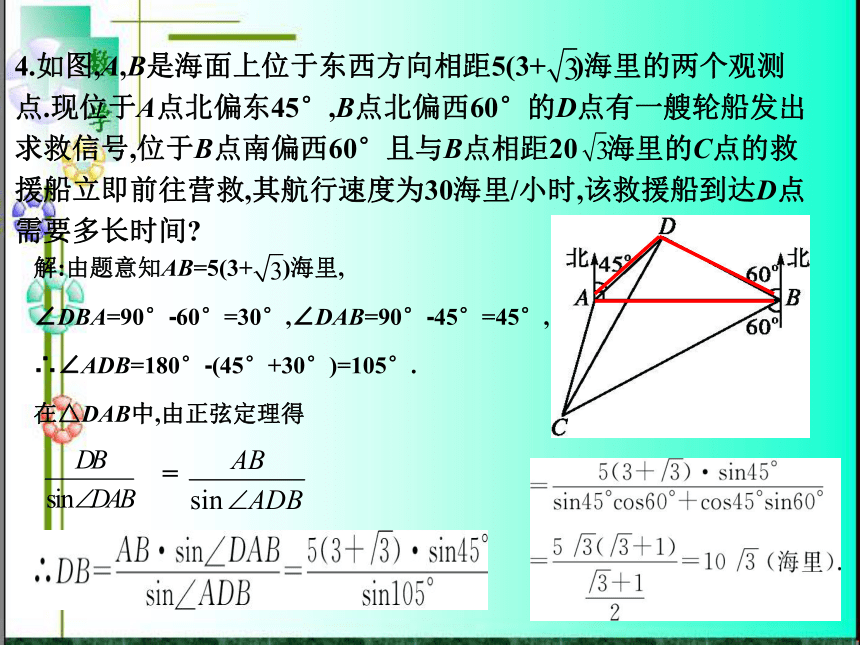
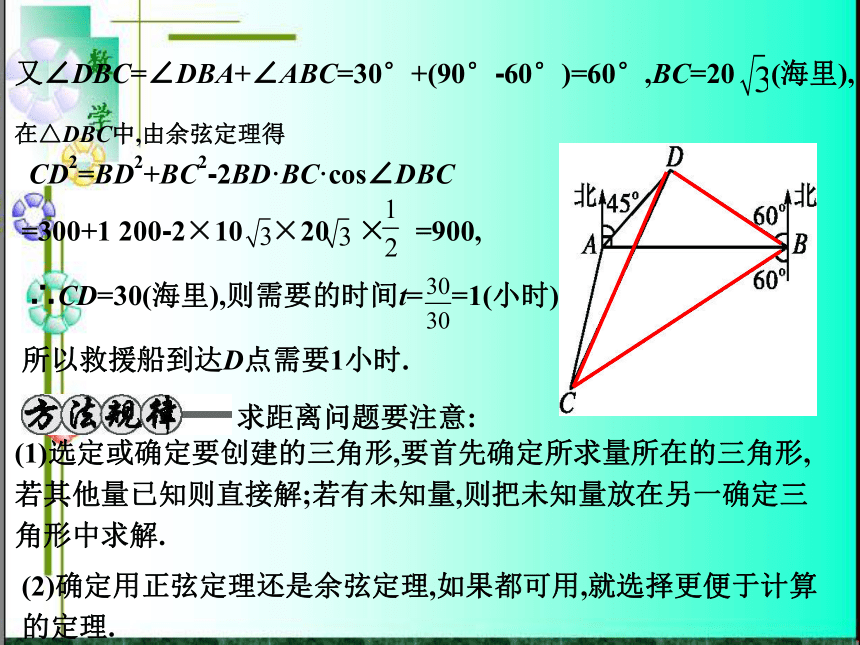
:AB=20,∠BAC=30°,∠BAD=40°,∴∠ ABC=105°,∴∠ACB=45°,由正弦定理得? =?.∴BC=? = = =10?.答案:A4.如图,A,B是海面上位于东西方向相距5(3+?)海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20?海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?解:由题意知AB=5(3+? )海里,∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,∴∠ADB=180°-(45°+30°)=105°.在△DAB中,由正弦定理得? =?又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC=20? (海里),在△DBC中,由余弦定理得CD2=BD2+BC2-2BD·BC·cos∠DBC=300+1 200-2×10?×20?×?=900,∴CD=30(海里),则需要的时间t=?=1(小时).所以救援船到达D点需要1小时.求距离问题要注意:(1)选定或确定要创建的三角形,要首先确定所求量所在的三角形,若其他量已知则直接解;若有未知量,则把未知量放在另一确定三角形中求解.(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.高度问题1.从一幢20 m高的楼顶测得对面一塔顶的仰角为60°,
塔基的俯角为45°,则塔高为?( ????)考点二AE=20 m,∠CAE=60°,∴CE=20? m.∴塔高为20+20?=20(1+?) m.答案:B解析:如图所示,2.如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,
则旗杆高AB为 ????.? 解析:在三角形BCD中,由正弦定理得? =? ?BC= ?a,
在直角三角形ABC中,AB=BCtan60°=?a×? =? a.aa3.(密码改编)某兴趣小组要测量电视塔AE的高度H(单位:m),如图所示,垂直放置的标杆BC的高度h=4 m,仰角∠ABE=α,∠ADE=β且测得tanα=1.24,tanβ=1.20,求H的值.解:由AB= ? ,BD= ? ,AD= ? 及AB+BD=AD,得? +? =?,因此,算出的电视塔的高度H是124 m.?4.要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的
∠BCD=120°,CD=40 m,求电视塔的高度.解:如图,设电视塔AB高为x m,则在Rt△ABC中,由∠ACB=45°得BC=x.
在Rt△ADB中,∠ADB=30°,∴BD=? x.在△BDC中,由余弦定理得,BD2=BC2+CD2-2BC·CD·cos120°,即(?x)2=x2+402-2·x·40·cos120°,解得x=40,∴电视塔高为40米.1. 在处理有关高度问题时,要理解仰角、俯角(视线在水平线上方、下方的角分别称为仰角、俯角)是一个关键.
2.在实际问题中,可能会遇到空间与平面(地面)同时研究的问题,这时最好画两个图形,一个空间图形,一个平面图形,这样处理起来既清楚又不容易搞错.角度问题1.从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β之间的关系是?(???)考点三站C的北偏东40°,灯塔B在观察站C的南偏东60°,则灯塔A在灯塔B的?(???)A.北偏东10°B.北偏西10°C.南偏东10° D.南偏西10°2.如图所示,已知两座灯塔A和B与海洋观察站C的距离相等,灯塔A在观察解析:由已知∠ACB=180°-40°-60°=80°,又AC=BC,∴∠A=∠ABC=50°,60°-50°=10°.∴灯塔A位于灯塔B的北偏西10°.答案:B3.如图,为了解某海域海底构造,在海平面内一条直线上的A、B、C三点进行测量.已知AB=50 m,BC=120 m,于A处测得水深AD=80 m,于B处测得水深在海岸A处,发现北偏东45°方向,距A处(?-1)海里的B处有一艘走私船,在
A处北偏西75°的方向,距离A处2海里的C处的缉私船奉命以10?海里/时的
速度追截走私船.此时,走私船正以10海里/时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?解:设缉私船用t h在D处追上走私船,则有CD=10? t, BD=10t,在△ABC中,∵AB=? -1,AC=2,∠BAC=120°,∴由余弦定理,得BC2=AB2+AC2-2AB·AC·cos∠BAC=
(?-1)2+22-2×(?-1)×2×cos120°=6.∴BC=?,且sin∠ABC=? ·sin∠BAC= ? ×? =?.∴∠ABC=45°,解析∴BC与正北方向垂直.∵∠CBD=90°+30°=120°.在△BCD中,由正弦定理,得sin∠BCD= = =?,∴∠BCD=30°,即缉私船沿东偏北30°方向能最快追上走私船.首先应明确方位角的含义,在解应用题时,分析题意,分清已知与所求,再根 据题意正确画出示意图,这是最关键、最重要的一步,通过这一步可将实际 问题转化成可用数学方法解决的问题,解题中也要注意体会正、余弦定理 “联袂”使用的优点.? 【真题·模拟】 (2011·上海高考,8)在相距2千米的A,B两点处测量目标C,若∠CAB=75°,∠CBA=60°,则A,C两点之间的距离为 ????千米命题 探究 :本题考查了在实际问题下,正、余弦定理的应用.规范解答 :如图,∠C=180°-60°-75°=45°.? 由正 弦定理? =? 得AC=解析? 原创预测:解:在△ABC中,可知∠ACB=45°,由正弦定理得:? =?,解得AC=15米.小结全课:
在解应用题时,分析题意,分清已知与所求,再根据题意正确画出示意图,这是最关键、最重要的一步,通过这一步可将实际问题转化成可用数学方法解决的问题,解题中也要注意体会正、余弦定理“联袂”使用的优点.(1)选定或确定要创建的三角形,要首先确定所求量所在的三角形,若其他量已知则直接解;若有未知量,则把未知量放在另一确定三角形中求解.(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.
视线在水平线上方的角叫仰角,
在水平线下方的角叫俯角(如图①).(2)方位角方位角指从正北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图②).(3)方向角将正北或正南方向作为起始方向旋转到目标的方向线所成的角
(一般指锐角)。(4)坡度:坡面与水平面所成的二面角的度数.仰角、俯角、方位角有什么区别?提示:三者的参照物不同,仰角与俯角是相对于水平线而言的,而方位角是相对于正北方向而言的.距离问题1.如图,设A、B两点在河的两岸,一测量者在A所在的河岸边选定一点C,在测出AC的距离为 50 m,∠ACB=45°,∠CAB=105°后,就可以计算出A、B两点的距离为?( ????)A.50? m B.50? mC.25? m D.? m解析:由题意知∠CBA=30°,由正弦定理得?
=? ,∴AB= = =50? m.答案:A考点一2.已知A、B两地的距离为10 km,B、C两地的距离为20 km,现测得∠ABC=120°,则A,C两地的距离为?( ????)A.10 km B.10? kmC.10? km D.10? km解析:由余弦定理得AC2=AB2+BC2-2AB·BC·cos∠ABC
=100+400-2×10×20×(- )=700,∴AC=10?.答案:DABC10km20kmABC=120°,?3.一艘海轮从A处出发,以每小时40海里的速度沿东偏南50°方向直线航行, 30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南 20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是?(??????)A.10? 海里 B.10? 海里C.20? 海里 D.20? 海里解析:由A、B、C的位置如图所示
:AB=20,∠BAC=30°,∠BAD=40°,∴∠ ABC=105°,∴∠ACB=45°,由正弦定理得? =?.∴BC=? = = =10?.答案:A4.如图,A,B是海面上位于东西方向相距5(3+?)海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20?海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?解:由题意知AB=5(3+? )海里,∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,∴∠ADB=180°-(45°+30°)=105°.在△DAB中,由正弦定理得? =?又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC=20? (海里),在△DBC中,由余弦定理得CD2=BD2+BC2-2BD·BC·cos∠DBC=300+1 200-2×10?×20?×?=900,∴CD=30(海里),则需要的时间t=?=1(小时).所以救援船到达D点需要1小时.求距离问题要注意:(1)选定或确定要创建的三角形,要首先确定所求量所在的三角形,若其他量已知则直接解;若有未知量,则把未知量放在另一确定三角形中求解.(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.高度问题1.从一幢20 m高的楼顶测得对面一塔顶的仰角为60°,
塔基的俯角为45°,则塔高为?( ????)考点二AE=20 m,∠CAE=60°,∴CE=20? m.∴塔高为20+20?=20(1+?) m.答案:B解析:如图所示,2.如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=a,并在点C测得旗杆顶A的仰角为60°,
则旗杆高AB为 ????.? 解析:在三角形BCD中,由正弦定理得? =? ?BC= ?a,
在直角三角形ABC中,AB=BCtan60°=?a×? =? a.aa3.(密码改编)某兴趣小组要测量电视塔AE的高度H(单位:m),如图所示,垂直放置的标杆BC的高度h=4 m,仰角∠ABE=α,∠ADE=β且测得tanα=1.24,tanβ=1.20,求H的值.解:由AB= ? ,BD= ? ,AD= ? 及AB+BD=AD,得? +? =?,因此,算出的电视塔的高度H是124 m.?4.要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的
∠BCD=120°,CD=40 m,求电视塔的高度.解:如图,设电视塔AB高为x m,则在Rt△ABC中,由∠ACB=45°得BC=x.
在Rt△ADB中,∠ADB=30°,∴BD=? x.在△BDC中,由余弦定理得,BD2=BC2+CD2-2BC·CD·cos120°,即(?x)2=x2+402-2·x·40·cos120°,解得x=40,∴电视塔高为40米.1. 在处理有关高度问题时,要理解仰角、俯角(视线在水平线上方、下方的角分别称为仰角、俯角)是一个关键.
2.在实际问题中,可能会遇到空间与平面(地面)同时研究的问题,这时最好画两个图形,一个空间图形,一个平面图形,这样处理起来既清楚又不容易搞错.角度问题1.从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β之间的关系是?(???)考点三站C的北偏东40°,灯塔B在观察站C的南偏东60°,则灯塔A在灯塔B的?(???)A.北偏东10°B.北偏西10°C.南偏东10° D.南偏西10°2.如图所示,已知两座灯塔A和B与海洋观察站C的距离相等,灯塔A在观察解析:由已知∠ACB=180°-40°-60°=80°,又AC=BC,∴∠A=∠ABC=50°,60°-50°=10°.∴灯塔A位于灯塔B的北偏西10°.答案:B3.如图,为了解某海域海底构造,在海平面内一条直线上的A、B、C三点进行测量.已知AB=50 m,BC=120 m,于A处测得水深AD=80 m,于B处测得水深在海岸A处,发现北偏东45°方向,距A处(?-1)海里的B处有一艘走私船,在
A处北偏西75°的方向,距离A处2海里的C处的缉私船奉命以10?海里/时的
速度追截走私船.此时,走私船正以10海里/时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?解:设缉私船用t h在D处追上走私船,则有CD=10? t, BD=10t,在△ABC中,∵AB=? -1,AC=2,∠BAC=120°,∴由余弦定理,得BC2=AB2+AC2-2AB·AC·cos∠BAC=
(?-1)2+22-2×(?-1)×2×cos120°=6.∴BC=?,且sin∠ABC=? ·sin∠BAC= ? ×? =?.∴∠ABC=45°,解析∴BC与正北方向垂直.∵∠CBD=90°+30°=120°.在△BCD中,由正弦定理,得sin∠BCD= = =?,∴∠BCD=30°,即缉私船沿东偏北30°方向能最快追上走私船.首先应明确方位角的含义,在解应用题时,分析题意,分清已知与所求,再根 据题意正确画出示意图,这是最关键、最重要的一步,通过这一步可将实际 问题转化成可用数学方法解决的问题,解题中也要注意体会正、余弦定理 “联袂”使用的优点.? 【真题·模拟】 (2011·上海高考,8)在相距2千米的A,B两点处测量目标C,若∠CAB=75°,∠CBA=60°,则A,C两点之间的距离为 ????千米命题 探究 :本题考查了在实际问题下,正、余弦定理的应用.规范解答 :如图,∠C=180°-60°-75°=45°.? 由正 弦定理? =? 得AC=解析? 原创预测:解:在△ABC中,可知∠ACB=45°,由正弦定理得:? =?,解得AC=15米.小结全课:
在解应用题时,分析题意,分清已知与所求,再根据题意正确画出示意图,这是最关键、最重要的一步,通过这一步可将实际问题转化成可用数学方法解决的问题,解题中也要注意体会正、余弦定理“联袂”使用的优点.(1)选定或确定要创建的三角形,要首先确定所求量所在的三角形,若其他量已知则直接解;若有未知量,则把未知量放在另一确定三角形中求解.(2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理.
