2021-2022学年高二上学期数学沪教版(2020)必修第三册第 13 章 统计 章节复习练习卷【2】
文档属性
| 名称 | 2021-2022学年高二上学期数学沪教版(2020)必修第三册第 13 章 统计 章节复习练习卷【2】 |  | |
| 格式 | doc | ||
| 文件大小 | 800.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 10:58:36 | ||
图片预览



文档简介
【学生版】
高二数学《第 13 章 统计》章节复习练习卷【2】
一、填空题(共10小题,每小题4分,满分40分)
1、为了了解某班学生会考成绩的合格率,要从该班45名学生中抽取20名学生的会考成绩进行分析,则在这次抽取中,总体为 ,样本为 ;
【提示】
【答案】
【说明】
2、一个容量为20的样本数据,分组与频数如下表:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 2 3 4 5 4 2
则样本在[10,50)内的频率为__________
【提示】
【答案】
【解析】
【说明】
3、小明从网上查询到某贫困地区10户居民家庭年收入(单位:万元)如下所示:
编号 1 2 3 4 5 6 7 8 9 10
年收入 1.2 1.3 1.8 2.0 4.6 1.7 0.9 2.1 1.0 1.6
根据以上数据,我们认为有一个数据是不准确的,需要剔除,这个数据是________
【提示】
【答案】
【解析】
【说明】
4、从观测所得到的数据中取出m个a,n个b,p个c组成一个样本,那么这个样本的平均数是________
【提示】
【答案】
【解析】
【说明】
5、10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,试比较a,b,c的大小
6、为了了解某校高中学生的近视眼发病率,在该校学生中进行分层抽样调查,已知该校高一、高二、高三分别有学生800名、600名、500名,若在高三学生中抽取25名,则在高一学生中抽取的人数是
7、为了解某小区老年人在一天中锻炼身体的时间,随机调查了50人,根据调查数据,画出了锻炼时间在0~2时的样本频率分布直方图(如图),则50人中锻炼身体的时间在区间[0.5,1.5)内的人数是
8、要调查某地区高中学生身体素质,从高中生中抽取100人进行跳高测试,根据测试成绩制作频率分布
直方图如图,现从成绩在[120,140)之间的学生中用分层抽样的方法抽取5人,应从[120,130)间抽取
人数为b,则实数a= ,b=
9、已知样本数据x1,x2,…,xn(n∈N*)的平均数与方差分别是和,若(i=1,2,…n),且样本数据y1,y2,…,yn的平均数与方差分别是和,则 =
10、某车间12名工人一天生产某产品(单位:kg)的数量分别为13.8,13,13.5,15.7,13.6,14.8,14,14.6,15,15.2,15.8,15.4,则所给数据的第25,50,75百分位数分别是___________.
二、选择题(共4小题 每小题4分,满分16分)
11、某工厂6名工人在一小时内生产零件的个数分别是11,12,13,15,15,18,设该组数据的平均数为,中位数为,则( )
A. B. C. D.
12、下表是“唱歌”比赛中12个班级的得分情况,则80百分位数是( )
班级得分 7 8 9 10 11 13 14
频数 2 1 2 3 1 2 1
A.13.5 B.10.5 C.12 D.13
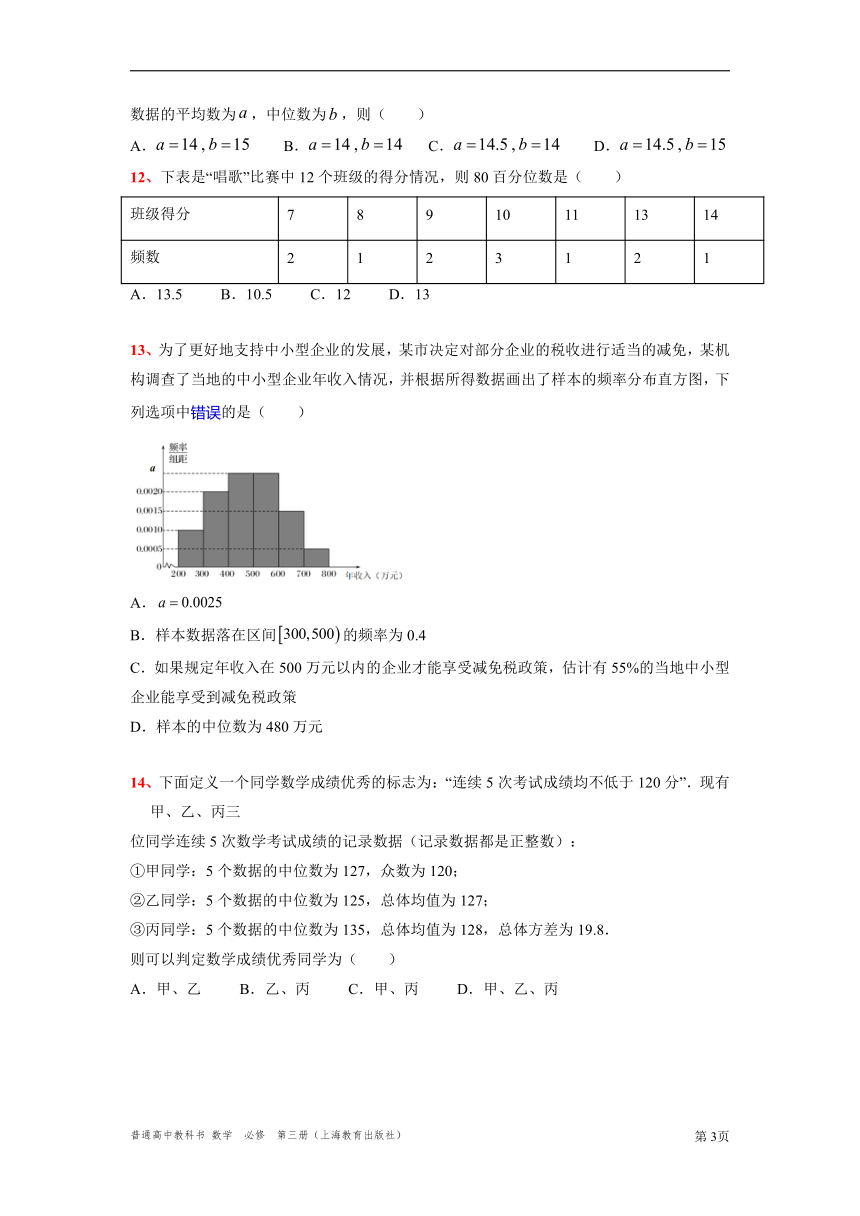
13、为了更好地支持中小型企业的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下列选项中错误的是( )
A.
B.样本数据落在区间的频率为0.4
C.如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策
D.样本的中位数为480万元
14、下面定义一个同学数学成绩优秀的标志为:“连续5次考试成绩均不低于120分”.现有甲、乙、丙三
位同学连续5次数学考试成绩的记录数据(记录数据都是正整数):
①甲同学:5个数据的中位数为127,众数为120;
②乙同学:5个数据的中位数为125,总体均值为127;
③丙同学:5个数据的中位数为135,总体均值为128,总体方差为19.8.
则可以判定数学成绩优秀同学为( )
A.甲、乙 B.乙、丙 C.甲、丙 D.甲、乙、丙
三、解答题(共4小题,满分44分;解答时应写出文字说明、证明过程或演算步骤)
15.(本题8分)
对甲、乙两名自行车手在相同条件下进行了6次测试,测得他们的最大速度的数据如下表;
甲 27 38 30[] 37 35 31
乙 33 29 38 34 28 36
(1)画出茎叶图,由茎叶图你能获得哪些信息
(2)分别求出甲、乙两名自行车手最大速度数据的平均数、标准差,并判断选谁参加比赛更合适;
16.(本题10分)
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
17.(本题满分12分)
如图是某校高三(1)班的一次数学知识竞赛成绩的基叶图
(图中仅列出[50,60),[90,100)的数据)
和频率分布直方图.
(1)求全班人数以及频率分布直方图中的x,y;
(2)估计学生竞赛成绩的平均数和中位数
(保留两位小数);
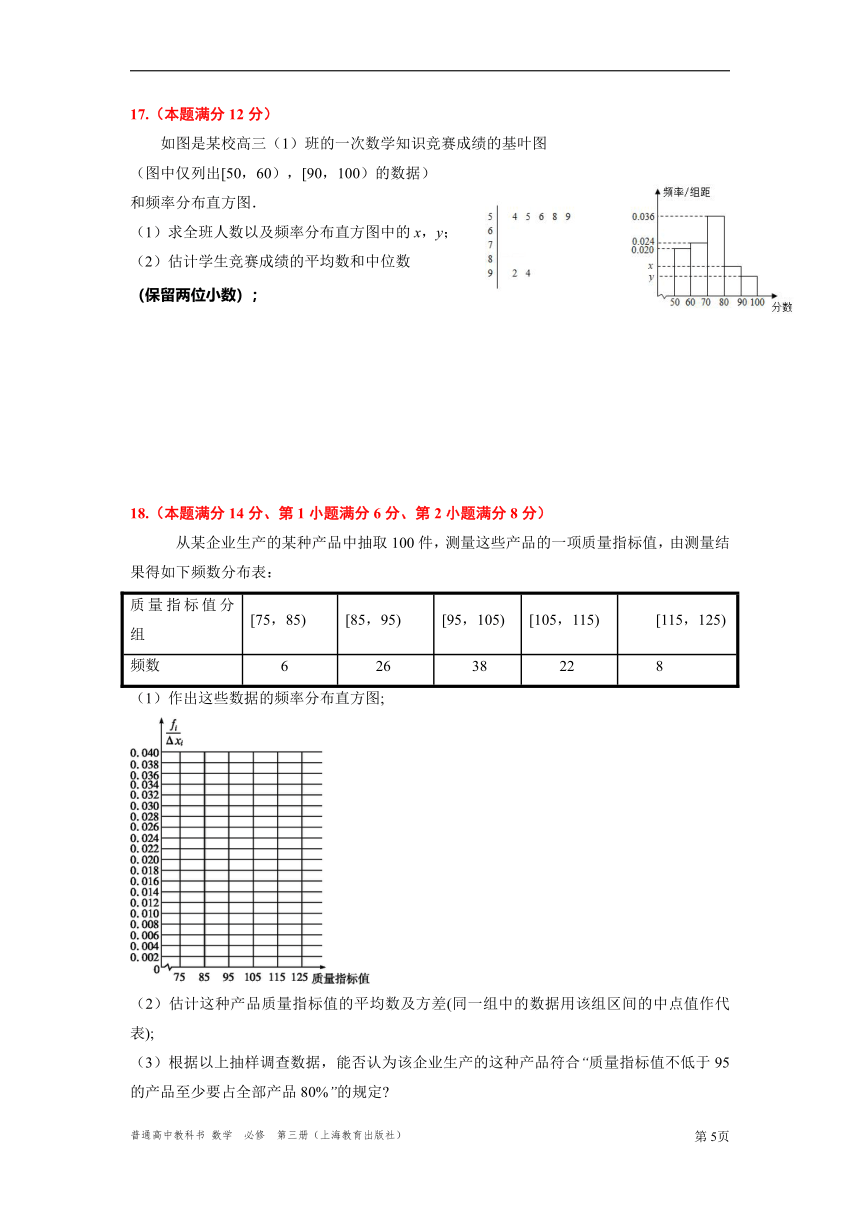
18.(本题满分14分、第1小题满分6分、第2小题满分8分)
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125)
频数 6 26 38 22 8
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定 [
【教师版】
高二数学《第 13 章 统计》章节复习练习卷【2】
一、填空题(共10小题,每小题4分,满分40分)
1、为了了解某班学生会考成绩的合格率,要从该班45名学生中抽取20名学生的会考成绩进行分析,则在这次抽取中,总体为 ,样本为 ;
【提示】知道概念总体、样本;
【答案】该班45名学生会考成绩的合格率;被抽取的20名学生会考成绩的合格率;
【说明】本题主要考查总体、样本基本概念;
2、一个容量为20的样本数据,分组与频数如下表:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 2 3 4 5 4 2
则样本在[10,50)内的频率为__________
【提示】知道样本频率的求法;用[10,50)的频数除以20求得[10,50)的频率;
【答案】0.7;
【解析】数据落在区间[10,50)的频率为;故答案为:0.7;
【说明】本题主要考查样本频率的求法;
3、小明从网上查询到某贫困地区10户居民家庭年收入(单位:万元)如下所示:
编号 1 2 3 4 5 6 7 8 9 10
年收入 1.2 1.3 1.8 2.0 4.6 1.7 0.9 2.1 1.0 1.6
根据以上数据,我们认为有一个数据是不准确的,需要剔除,这个数据是________
【提示】注意:根据表格中的数据,找出明显高于或低于其他数据的数;
【答案】
【解析】根据表格中的数据,可得编号为5,年收入4.6,明显高于其他数据,所以这个数据不准确的,需要剔除;故答案为:;
【说明】主要是去除“极端”数值,提高利用样本评估总体的精确性;
4、从观测所得到的数据中取出m个a,n个b,p个c组成一个样本,那么这个样本的平均数是________
【提示】注意利用根据数据平均数的计算公式;
【答案】;
【解析】由题意,数据中取出m个a,n个b,p个c组成一个样本,可得样本中个体数为,
可得数据总和为,故平均数为,故答案为:;
【说明】本题主要考查平均数的概念与计算方法;
5、10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,试比较a,b,c的大小
【提示】知道样本的数字特征及其计算方法;
【答案】c>b>a;
【解析】该组数据为:10,12,14,14,15,15,16,17,17,17,
因此平均数a=14.7,中位数b==15,众数c=17,故a【说明】本题考查样本的平均数、中位数、众数的计算方法;
6、为了了解某校高中学生的近视眼发病率,在该校学生中进行分层抽样调查,已知该校高一、高二、高三分别有学生800名、600名、500名,若在高三学生中抽取25名,则在高一学生中抽取的人数是
【提示】注意:分层抽样的方法;
【答案】40
【解析】设在高一学生中抽取的人数为x,则有,解得x=40;
【说明】本题主要考查分层抽样的样本数计算方法;
7、为了解某小区老年人在一天中锻炼身体的时间,随机调查了50人,根据调查数据,画出了锻炼时间在0~2时的样本频率分布直方图(如图),则50人中锻炼身体的时间在区间[0.5,1.5)内的人数是
【提示】会识图;
【答案】35;
【解析】在区间[0.5,1.5)内的频率为(0.8+0.6)×0.5=0.7,人数为0.7×50=35;
【说明】本题考查对频率直方图的绘制步骤的认识;
8、要调查某地区高中学生身体素质,从高中生中抽取100人进行跳高测试,根据测试成绩制作频率分布
直方图如图,现从成绩在[120,140)之间的学生中用分层抽样的方法抽取5人,应从[120,130)间抽取
人数为b,则实数a= ,b=
【提示】从图中收集需要的数据
【答案】a=0.030,b=3;
【解析】由题得10×(0.005+0.035+a+0.020+0.010)=1,所以a=0.030.
在[120,130)之间的学生人数为:100×10×0.030=30人,
在[130,140)之间的学生人数为:100×10×0.020=20人,
在[120,140)之间的学生人数为:100×(10×0.030+0.020)=50人,
又用分层抽样的方法在[120,140)之间的学生50人中抽取5人,即抽取比例为:;
所以成绩在[120,130)之间的学生中抽取的人数应,,即b=3,
【说明】本题是频率直方图与分层抽样的交汇;
9、已知样本数据x1,x2,…,xn(n∈N*)的平均数与方差分别是和,若(i=1,2,…n),且样本数据y1,y2,…,yn的平均数与方差分别是和,则 =
【提示】知道样本的平均数与方差及其计算公式;
【答案】1;
【解析】由平均数与方差计算公式及其性质,得,解得:,故;
【说明】本题考查对样本平均数与方差及其性质的理解;
10、某车间12名工人一天生产某产品(单位:kg)的数量分别为13.8,13,13.5,15.7,13.6,14.8,14,14.6,15,15.2,15.8,15.4,则所给数据的第25,50,75百分位数分别是___________.
【提示】知道百分位数;所给数据的第25,50,75百分位数分别是:第3个数据与第4个数据的平均数、第6个数据与第7个数据的平均数、第9个数据和第10个数据的平均数,进而可得答案;
【答案】13.7;14.7;15.3;
【解析】将12个数据按从小到大排序:
13,13.5,13.6,13.8,14,14.6,14.8,15,15.2,15.4,15.7,15.8.
由i=12×25%=3,得所给数据的第25百分位数是第3个数据与第4个数据的平均数即=13.7;
由i=12×50%=6,得的给数据的第50百分位数是第6个数据与第7个数据的平均数,即=14.7;
由i=12×75%=9,得所给数据的第75百分位数是第9个数据和第10个数据的平均数,即=15.3.
故答案为:13.7,14.7,15.3
【说明】本题考查百分位数的求解要求;
二、选择题(共4小题 每小题4分,满分16分)
11、某工厂6名工人在一小时内生产零件的个数分别是11,12,13,15,15,18,设该组数据的平均数为,中位数为,则( )
A. B. C. D.
【提示】注意:将数按次序排列;
【答案】B
【解析】平均数为,由这6个数分别是11,12,13,15,15,18,
则其中位数为14;故选:B;
【说明】本题考查平均数、中位数的概念与求法;
12、下表是“唱歌”比赛中12个班级的得分情况,则80百分位数是( )
班级得分 7 8 9 10 11 13 14
频数 2 1 2 3 1 2 1
A.13.5 B.10.5 C.12 D.13
【提示】注意:将数按次序排列;
【答案】D
【解析】因为,12个班级的得分按照从小到大排序,可得80百分位数是13;
故选:D;
【说明】本题考查百分位数的概念与求法;
13、为了更好地支持中小型企业的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下列选项中错误的是( )
A.
B.样本数据落在区间的频率为0.4
C.如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策
D.样本的中位数为480万元
【提示】了解相关的统计概念、制作方法、操作步骤;
【答案】B
【解析】由频率分布直方图,可得,
解得,所以A正确;
样本数据落在区间的频率为,所以B错误;
样本数据落在区间的频率为,所以C正确;
样本数据落在区间的频率为0.3,落在区间的频率为0.55,
所以中位数在区间内故中位数为(万元),
所以D正确.
故选:B;
【说明】本题综合考查了统计的概念与计算公式;
14、下面定义一个同学数学成绩优秀的标志为:“连续5次考试成绩均不低于120分”.现有甲、乙、丙三
位同学连续5次数学考试成绩的记录数据(记录数据都是正整数):
①甲同学:5个数据的中位数为127,众数为120;
②乙同学:5个数据的中位数为125,总体均值为127;
③丙同学:5个数据的中位数为135,总体均值为128,总体方差为19.8.
则可以判定数学成绩优秀同学为( )
A.甲、乙 B.乙、丙 C.甲、丙 D.甲、乙、丙
【提示】注意:样本数据处理的方法与要求;
【答案】C;
【解析】在①中,甲同学:5个数据的中位数为127,众数为120,
所以前三个数为120,120,127,则后两个数肯定大于127,
故甲同学数学成绩优秀,故①成立;
在②中,5个数据的中位数为125,总体均值为127,
可以找到很多反例,如:118,119,125,128,145,
故乙同学数学成绩不优秀,故②不成立;
在③中,5个数据的中位数为135,总体均值为128,总体方差为19.8
设x1<x2<x3<x4,
则丙的方差为[(x1﹣128)2+(x2﹣128)2+(x3﹣128)2+(x4﹣128)2+(135﹣128)2]=19.8,
所以,(x1﹣128)2+(x2﹣128)2+(x3﹣128)2+(x4﹣128)2=50,则(x1﹣128)2≤50,
得|x1﹣128|≤5,∴x1≥128﹣5>120,所以,丙同学数学成绩优秀,故③成立.
所以,数学成绩优秀有甲和丙2个同学;
【说明】结合代数运算进行数据处理,用数据说事;
三、解答题(共4小题,满分44分;解答时应写出文字说明、证明过程或演算步骤)
15.(本题8分)
对甲、乙两名自行车手在相同条件下进行了6次测试,测得他们的最大速度的数据如下表;
甲 27 38 30[] 37 35 31
乙 33 29 38 34 28 36
(1)画出茎叶图,由茎叶图你能获得哪些信息
(2)分别求出甲、乙两名自行车手最大速度数据的平均数、标准差,并判断选谁参加比赛更合适;
【提示】理解绘制茎叶图的方法与会计算样本的数据特征;
【解析】(1)画茎叶图如图所示,从这个茎叶图可以看出,乙的得分比较均匀,发挥比较稳定;乙的中位数是33.5,甲的中位数是33,因此乙的总体得分情况比甲好;
(2)根据表中数据得=33,=33;s甲≈3.96,s乙≈3.56,比较可知,选乙参加比赛比较合适;
【说明】本题考查了茎叶图的制作方法与利用样本的数据特征进行合理的判断;
16.(本题10分)
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
【提示】会识图与收集数据;
【解析】(1)众数是最高小矩形中点的横坐标,所以众数为m=75(分);(3分)
前三个小矩形面积为0.01×10+0.015×10+0.015×10=0.4,
因为,中位数要平分直方图的面积,所以,(7分)
(2)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为 (0.015+0.03+0.025+0.005)×10=0.75
所以,抽样学生成绩的合格率是75% (11分)
利用组中值估算抽样学生的平均分
45 f1+55 f2+65 f3+75 f4+85 f5+95 f6=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71
估计这次考试的平均分是71分.(14分)
17.(本题满分12分)
如图是某校高三(1)班的一次数学知识竞赛成绩的基叶图
(图中仅列出[50,60),[90,100)的数据)
和频率分布直方图.
(1)求全班人数以及频率分布直方图中的x,y;
(2)估计学生竞赛成绩的平均数和中位数
(保留两位小数);
【解析】(1)分数在[50,60)的频率为0.020×10=0.2,由茎叶图知,分数在[50,60)之间的频数为5,
所以全班人数为(人);
分数在[90,100)之间的频数为2,由,解得y=0.008;
又10x=1﹣10×(0.036+0.024+0.020+0.008),解得x=0.012.
(2)由频率分布直方图,计算平均数为
55×0.2+65×0.24+75×0.36+85×0.12+95×0.08=71.4,
由0.2+0.24+0.36=0.80,所以中位数在[70,80)内,
设中位数为m,则0.20+0.24+(m﹣70)×0.036=0.5,解得m≈71.67,所以中位数约为71.67。
18.(本题满分14分、第1小题满分6分、第2小题满分8分)
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125)
频数 6 26 38 22 8
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定 [
【解析】(1)频率分布直方图如下:
(2)质量指标值的样本平均数为
80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
质量指标值的样本方差为s2=(-20)2×0.06+(-10)2×0.26+0×0.38+102×0.22+202×0.08=104.
所以这种产品质量指标值的平均数的估计值为100,方差的估计值为104.
(3)质量指标值不低于95的产品所占比例的估计值为0.38+0.22+0.08=0.68.
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.
PAGE
第2页
普通高中教科书 数学 必修 第三册(上海教育出版社)
高二数学《第 13 章 统计》章节复习练习卷【2】
一、填空题(共10小题,每小题4分,满分40分)
1、为了了解某班学生会考成绩的合格率,要从该班45名学生中抽取20名学生的会考成绩进行分析,则在这次抽取中,总体为 ,样本为 ;
【提示】
【答案】
【说明】
2、一个容量为20的样本数据,分组与频数如下表:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 2 3 4 5 4 2
则样本在[10,50)内的频率为__________
【提示】
【答案】
【解析】
【说明】
3、小明从网上查询到某贫困地区10户居民家庭年收入(单位:万元)如下所示:
编号 1 2 3 4 5 6 7 8 9 10
年收入 1.2 1.3 1.8 2.0 4.6 1.7 0.9 2.1 1.0 1.6
根据以上数据,我们认为有一个数据是不准确的,需要剔除,这个数据是________
【提示】
【答案】
【解析】
【说明】
4、从观测所得到的数据中取出m个a,n个b,p个c组成一个样本,那么这个样本的平均数是________
【提示】
【答案】
【解析】
【说明】
5、10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,试比较a,b,c的大小
6、为了了解某校高中学生的近视眼发病率,在该校学生中进行分层抽样调查,已知该校高一、高二、高三分别有学生800名、600名、500名,若在高三学生中抽取25名,则在高一学生中抽取的人数是
7、为了解某小区老年人在一天中锻炼身体的时间,随机调查了50人,根据调查数据,画出了锻炼时间在0~2时的样本频率分布直方图(如图),则50人中锻炼身体的时间在区间[0.5,1.5)内的人数是
8、要调查某地区高中学生身体素质,从高中生中抽取100人进行跳高测试,根据测试成绩制作频率分布
直方图如图,现从成绩在[120,140)之间的学生中用分层抽样的方法抽取5人,应从[120,130)间抽取
人数为b,则实数a= ,b=
9、已知样本数据x1,x2,…,xn(n∈N*)的平均数与方差分别是和,若(i=1,2,…n),且样本数据y1,y2,…,yn的平均数与方差分别是和,则 =
10、某车间12名工人一天生产某产品(单位:kg)的数量分别为13.8,13,13.5,15.7,13.6,14.8,14,14.6,15,15.2,15.8,15.4,则所给数据的第25,50,75百分位数分别是___________.
二、选择题(共4小题 每小题4分,满分16分)
11、某工厂6名工人在一小时内生产零件的个数分别是11,12,13,15,15,18,设该组数据的平均数为,中位数为,则( )
A. B. C. D.
12、下表是“唱歌”比赛中12个班级的得分情况,则80百分位数是( )
班级得分 7 8 9 10 11 13 14
频数 2 1 2 3 1 2 1
A.13.5 B.10.5 C.12 D.13
13、为了更好地支持中小型企业的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下列选项中错误的是( )
A.
B.样本数据落在区间的频率为0.4
C.如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策
D.样本的中位数为480万元
14、下面定义一个同学数学成绩优秀的标志为:“连续5次考试成绩均不低于120分”.现有甲、乙、丙三
位同学连续5次数学考试成绩的记录数据(记录数据都是正整数):
①甲同学:5个数据的中位数为127,众数为120;
②乙同学:5个数据的中位数为125,总体均值为127;
③丙同学:5个数据的中位数为135,总体均值为128,总体方差为19.8.
则可以判定数学成绩优秀同学为( )
A.甲、乙 B.乙、丙 C.甲、丙 D.甲、乙、丙
三、解答题(共4小题,满分44分;解答时应写出文字说明、证明过程或演算步骤)
15.(本题8分)
对甲、乙两名自行车手在相同条件下进行了6次测试,测得他们的最大速度的数据如下表;
甲 27 38 30[] 37 35 31
乙 33 29 38 34 28 36
(1)画出茎叶图,由茎叶图你能获得哪些信息
(2)分别求出甲、乙两名自行车手最大速度数据的平均数、标准差,并判断选谁参加比赛更合适;
16.(本题10分)
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
17.(本题满分12分)
如图是某校高三(1)班的一次数学知识竞赛成绩的基叶图
(图中仅列出[50,60),[90,100)的数据)
和频率分布直方图.
(1)求全班人数以及频率分布直方图中的x,y;
(2)估计学生竞赛成绩的平均数和中位数
(保留两位小数);
18.(本题满分14分、第1小题满分6分、第2小题满分8分)
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125)
频数 6 26 38 22 8
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定 [
【教师版】
高二数学《第 13 章 统计》章节复习练习卷【2】
一、填空题(共10小题,每小题4分,满分40分)
1、为了了解某班学生会考成绩的合格率,要从该班45名学生中抽取20名学生的会考成绩进行分析,则在这次抽取中,总体为 ,样本为 ;
【提示】知道概念总体、样本;
【答案】该班45名学生会考成绩的合格率;被抽取的20名学生会考成绩的合格率;
【说明】本题主要考查总体、样本基本概念;
2、一个容量为20的样本数据,分组与频数如下表:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 2 3 4 5 4 2
则样本在[10,50)内的频率为__________
【提示】知道样本频率的求法;用[10,50)的频数除以20求得[10,50)的频率;
【答案】0.7;
【解析】数据落在区间[10,50)的频率为;故答案为:0.7;
【说明】本题主要考查样本频率的求法;
3、小明从网上查询到某贫困地区10户居民家庭年收入(单位:万元)如下所示:
编号 1 2 3 4 5 6 7 8 9 10
年收入 1.2 1.3 1.8 2.0 4.6 1.7 0.9 2.1 1.0 1.6
根据以上数据,我们认为有一个数据是不准确的,需要剔除,这个数据是________
【提示】注意:根据表格中的数据,找出明显高于或低于其他数据的数;
【答案】
【解析】根据表格中的数据,可得编号为5,年收入4.6,明显高于其他数据,所以这个数据不准确的,需要剔除;故答案为:;
【说明】主要是去除“极端”数值,提高利用样本评估总体的精确性;
4、从观测所得到的数据中取出m个a,n个b,p个c组成一个样本,那么这个样本的平均数是________
【提示】注意利用根据数据平均数的计算公式;
【答案】;
【解析】由题意,数据中取出m个a,n个b,p个c组成一个样本,可得样本中个体数为,
可得数据总和为,故平均数为,故答案为:;
【说明】本题主要考查平均数的概念与计算方法;
5、10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,试比较a,b,c的大小
【提示】知道样本的数字特征及其计算方法;
【答案】c>b>a;
【解析】该组数据为:10,12,14,14,15,15,16,17,17,17,
因此平均数a=14.7,中位数b==15,众数c=17,故a
6、为了了解某校高中学生的近视眼发病率,在该校学生中进行分层抽样调查,已知该校高一、高二、高三分别有学生800名、600名、500名,若在高三学生中抽取25名,则在高一学生中抽取的人数是
【提示】注意:分层抽样的方法;
【答案】40
【解析】设在高一学生中抽取的人数为x,则有,解得x=40;
【说明】本题主要考查分层抽样的样本数计算方法;
7、为了解某小区老年人在一天中锻炼身体的时间,随机调查了50人,根据调查数据,画出了锻炼时间在0~2时的样本频率分布直方图(如图),则50人中锻炼身体的时间在区间[0.5,1.5)内的人数是
【提示】会识图;
【答案】35;
【解析】在区间[0.5,1.5)内的频率为(0.8+0.6)×0.5=0.7,人数为0.7×50=35;
【说明】本题考查对频率直方图的绘制步骤的认识;
8、要调查某地区高中学生身体素质,从高中生中抽取100人进行跳高测试,根据测试成绩制作频率分布
直方图如图,现从成绩在[120,140)之间的学生中用分层抽样的方法抽取5人,应从[120,130)间抽取
人数为b,则实数a= ,b=
【提示】从图中收集需要的数据
【答案】a=0.030,b=3;
【解析】由题得10×(0.005+0.035+a+0.020+0.010)=1,所以a=0.030.
在[120,130)之间的学生人数为:100×10×0.030=30人,
在[130,140)之间的学生人数为:100×10×0.020=20人,
在[120,140)之间的学生人数为:100×(10×0.030+0.020)=50人,
又用分层抽样的方法在[120,140)之间的学生50人中抽取5人,即抽取比例为:;
所以成绩在[120,130)之间的学生中抽取的人数应,,即b=3,
【说明】本题是频率直方图与分层抽样的交汇;
9、已知样本数据x1,x2,…,xn(n∈N*)的平均数与方差分别是和,若(i=1,2,…n),且样本数据y1,y2,…,yn的平均数与方差分别是和,则 =
【提示】知道样本的平均数与方差及其计算公式;
【答案】1;
【解析】由平均数与方差计算公式及其性质,得,解得:,故;
【说明】本题考查对样本平均数与方差及其性质的理解;
10、某车间12名工人一天生产某产品(单位:kg)的数量分别为13.8,13,13.5,15.7,13.6,14.8,14,14.6,15,15.2,15.8,15.4,则所给数据的第25,50,75百分位数分别是___________.
【提示】知道百分位数;所给数据的第25,50,75百分位数分别是:第3个数据与第4个数据的平均数、第6个数据与第7个数据的平均数、第9个数据和第10个数据的平均数,进而可得答案;
【答案】13.7;14.7;15.3;
【解析】将12个数据按从小到大排序:
13,13.5,13.6,13.8,14,14.6,14.8,15,15.2,15.4,15.7,15.8.
由i=12×25%=3,得所给数据的第25百分位数是第3个数据与第4个数据的平均数即=13.7;
由i=12×50%=6,得的给数据的第50百分位数是第6个数据与第7个数据的平均数,即=14.7;
由i=12×75%=9,得所给数据的第75百分位数是第9个数据和第10个数据的平均数,即=15.3.
故答案为:13.7,14.7,15.3
【说明】本题考查百分位数的求解要求;
二、选择题(共4小题 每小题4分,满分16分)
11、某工厂6名工人在一小时内生产零件的个数分别是11,12,13,15,15,18,设该组数据的平均数为,中位数为,则( )
A. B. C. D.
【提示】注意:将数按次序排列;
【答案】B
【解析】平均数为,由这6个数分别是11,12,13,15,15,18,
则其中位数为14;故选:B;
【说明】本题考查平均数、中位数的概念与求法;
12、下表是“唱歌”比赛中12个班级的得分情况,则80百分位数是( )
班级得分 7 8 9 10 11 13 14
频数 2 1 2 3 1 2 1
A.13.5 B.10.5 C.12 D.13
【提示】注意:将数按次序排列;
【答案】D
【解析】因为,12个班级的得分按照从小到大排序,可得80百分位数是13;
故选:D;
【说明】本题考查百分位数的概念与求法;
13、为了更好地支持中小型企业的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下列选项中错误的是( )
A.
B.样本数据落在区间的频率为0.4
C.如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策
D.样本的中位数为480万元
【提示】了解相关的统计概念、制作方法、操作步骤;
【答案】B
【解析】由频率分布直方图,可得,
解得,所以A正确;
样本数据落在区间的频率为,所以B错误;
样本数据落在区间的频率为,所以C正确;
样本数据落在区间的频率为0.3,落在区间的频率为0.55,
所以中位数在区间内故中位数为(万元),
所以D正确.
故选:B;
【说明】本题综合考查了统计的概念与计算公式;
14、下面定义一个同学数学成绩优秀的标志为:“连续5次考试成绩均不低于120分”.现有甲、乙、丙三
位同学连续5次数学考试成绩的记录数据(记录数据都是正整数):
①甲同学:5个数据的中位数为127,众数为120;
②乙同学:5个数据的中位数为125,总体均值为127;
③丙同学:5个数据的中位数为135,总体均值为128,总体方差为19.8.
则可以判定数学成绩优秀同学为( )
A.甲、乙 B.乙、丙 C.甲、丙 D.甲、乙、丙
【提示】注意:样本数据处理的方法与要求;
【答案】C;
【解析】在①中,甲同学:5个数据的中位数为127,众数为120,
所以前三个数为120,120,127,则后两个数肯定大于127,
故甲同学数学成绩优秀,故①成立;
在②中,5个数据的中位数为125,总体均值为127,
可以找到很多反例,如:118,119,125,128,145,
故乙同学数学成绩不优秀,故②不成立;
在③中,5个数据的中位数为135,总体均值为128,总体方差为19.8
设x1<x2<x3<x4,
则丙的方差为[(x1﹣128)2+(x2﹣128)2+(x3﹣128)2+(x4﹣128)2+(135﹣128)2]=19.8,
所以,(x1﹣128)2+(x2﹣128)2+(x3﹣128)2+(x4﹣128)2=50,则(x1﹣128)2≤50,
得|x1﹣128|≤5,∴x1≥128﹣5>120,所以,丙同学数学成绩优秀,故③成立.
所以,数学成绩优秀有甲和丙2个同学;
【说明】结合代数运算进行数据处理,用数据说事;
三、解答题(共4小题,满分44分;解答时应写出文字说明、证明过程或演算步骤)
15.(本题8分)
对甲、乙两名自行车手在相同条件下进行了6次测试,测得他们的最大速度的数据如下表;
甲 27 38 30[] 37 35 31
乙 33 29 38 34 28 36
(1)画出茎叶图,由茎叶图你能获得哪些信息
(2)分别求出甲、乙两名自行车手最大速度数据的平均数、标准差,并判断选谁参加比赛更合适;
【提示】理解绘制茎叶图的方法与会计算样本的数据特征;
【解析】(1)画茎叶图如图所示,从这个茎叶图可以看出,乙的得分比较均匀,发挥比较稳定;乙的中位数是33.5,甲的中位数是33,因此乙的总体得分情况比甲好;
(2)根据表中数据得=33,=33;s甲≈3.96,s乙≈3.56,比较可知,选乙参加比赛比较合适;
【说明】本题考查了茎叶图的制作方法与利用样本的数据特征进行合理的判断;
16.(本题10分)
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
【提示】会识图与收集数据;
【解析】(1)众数是最高小矩形中点的横坐标,所以众数为m=75(分);(3分)
前三个小矩形面积为0.01×10+0.015×10+0.015×10=0.4,
因为,中位数要平分直方图的面积,所以,(7分)
(2)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为 (0.015+0.03+0.025+0.005)×10=0.75
所以,抽样学生成绩的合格率是75% (11分)
利用组中值估算抽样学生的平均分
45 f1+55 f2+65 f3+75 f4+85 f5+95 f6=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71
估计这次考试的平均分是71分.(14分)
17.(本题满分12分)
如图是某校高三(1)班的一次数学知识竞赛成绩的基叶图
(图中仅列出[50,60),[90,100)的数据)
和频率分布直方图.
(1)求全班人数以及频率分布直方图中的x,y;
(2)估计学生竞赛成绩的平均数和中位数
(保留两位小数);
【解析】(1)分数在[50,60)的频率为0.020×10=0.2,由茎叶图知,分数在[50,60)之间的频数为5,
所以全班人数为(人);
分数在[90,100)之间的频数为2,由,解得y=0.008;
又10x=1﹣10×(0.036+0.024+0.020+0.008),解得x=0.012.
(2)由频率分布直方图,计算平均数为
55×0.2+65×0.24+75×0.36+85×0.12+95×0.08=71.4,
由0.2+0.24+0.36=0.80,所以中位数在[70,80)内,
设中位数为m,则0.20+0.24+(m﹣70)×0.036=0.5,解得m≈71.67,所以中位数约为71.67。
18.(本题满分14分、第1小题满分6分、第2小题满分8分)
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125)
频数 6 26 38 22 8
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定 [
【解析】(1)频率分布直方图如下:
(2)质量指标值的样本平均数为
80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
质量指标值的样本方差为s2=(-20)2×0.06+(-10)2×0.26+0×0.38+102×0.22+202×0.08=104.
所以这种产品质量指标值的平均数的估计值为100,方差的估计值为104.
(3)质量指标值不低于95的产品所占比例的估计值为0.38+0.22+0.08=0.68.
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.
PAGE
第2页
普通高中教科书 数学 必修 第三册(上海教育出版社)
同课章节目录
