2021-2022学年高二上学期数学沪教版(2020)必修第三册第 13 章 统计 章节复习练习卷【4】
文档属性
| 名称 | 2021-2022学年高二上学期数学沪教版(2020)必修第三册第 13 章 统计 章节复习练习卷【4】 |

|
|
| 格式 | doc | ||
| 文件大小 | 788.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 00:00:00 | ||
图片预览




文档简介
【学生版】
高二数学《第 13 章 统计》章节复习练习卷【4】
一、填空题(共10小题,每小题4分,满分40分)
1、某公司员工对户外运动分别持“喜欢”“不喜欢”和“一般”三种态度,其中持“一般”态度的比持“不喜欢”态度的多12人,按分层抽样方法从该公司全体员工中选出部分员工座谈户外运动,如果选出的人有6位对户外运动持“喜欢”态度,有1位对户外运动持“不喜欢”态度,有3位对户外运动持“一般”态度,那么这个公司全体员工中对户外运动持“喜欢”态度的有 人。
【提示】
【答案】
【解析】
【说明】
2、某中学有高中生3 000人,初中生2 000人,男、女生所占的比例如下图所示,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取女生21人,则从初中生中抽取的男生人数是 人
【提示】
【答案】
【解析】
【说明】
3、某校进行教学竞赛,将考生的成绩分成90分以下、90~120分、120~150分三种情况进行统计,发现三个成绩段的人数之比依次为5?3?1,现用分层抽样的方法抽出一个容量为m的样本,其中分数在90~120分的人数是45,则此样本的容量m=
【提示】
【答案】
【解析】
【说明】
4、我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人等六项专项附加扣除,某单位老年、中年、青年员工分别有80人、100人、120人,现采用分层随机抽样的方法,从该单位上述员工中抽取30人调查专项附加扣除的享受情况,则应该从青年员工中抽取的人数为 人;
5、总体由编号为00,01,…,28,29的30个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第6列和第7列开始由左到右依次选取两个数字.则选出来的第5个个体的编号
为
0842 2689 5319 6450 9303 2320 9025 6015
9901 9025 2909 0937 6707 1528 3113 1165
0280 7999 7080 1573 6147 6403 2366 5398
6、已知样本数据,,,,的方差为2,则样本数据,,,,的方差为______.
7、某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则的值为 .
8、将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91;现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示:
则7个剩余分数的方差为
9、已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量为 (人)和抽取的高中生近视人数分别
为 (人)
10、某田径队6位运动员的体测成绩如下:甲78,乙86,丙64,丁77,戊83,己93.现从中挑选3位运动员参加集体赛,挑选条件为:
①丁一定要参加;
②3人的体测成绩总分要超过240(不含240);
③3人的体测成绩方差要小.
那么参加集体赛3人名单应为
二、选择题(共4小题 每小题4分,满分16分)
11、在“世界读书日”前夕,为了了解某地5 000名居民某天的阅读时间,从中抽取了200名居民的阅读时间进行统计分析.在这个问题中,5 000名居民的阅读时间的全体是( )
A.总体 B.个体 C.样本的容量 D.从总体中抽取的一个样本
12、某校高一、高二、高三共有学生1 800名,为了了解同学们对“某某”授课软件的意见,计划采用分层抽样的方法从这1 800名学生中抽取一个容量为72的样本.若从高一、高二、高三抽取的人数恰好是从小到大排列的连续偶数,则我校高三年级的人数为( )
A.800 B.750 C.700 D.650
13、利用简单随机抽样,从n个个体中抽取一个容量为10的样本.若第二次抽取时,余下的每个个体被抽到的概率为,则在整个抽样过程中,每个个体被抽到的概率为( )
A. B. C. D.
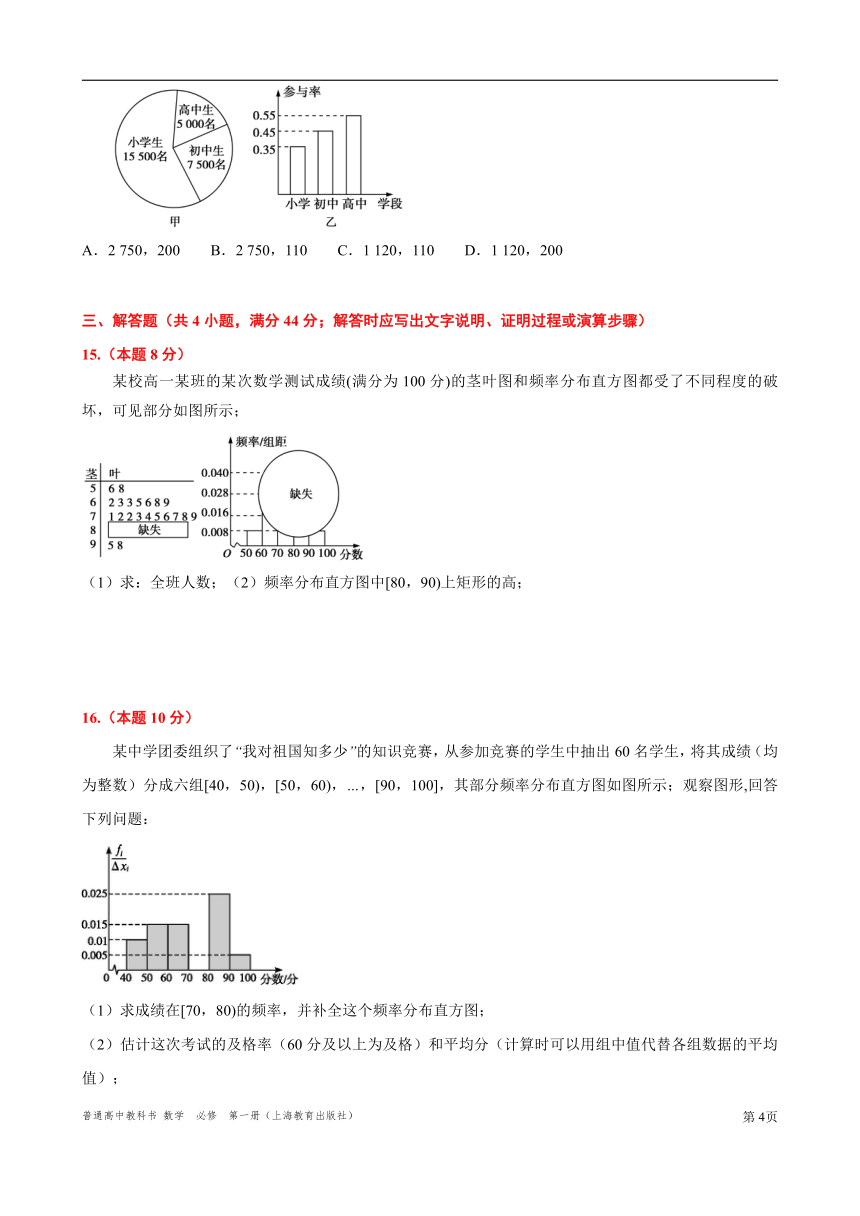
14、2020年初,我国突发新冠肺炎疫情,疫情期间中小学生“停课不停学”.已知某地区中小学生人数情况如甲图所示,各学段学生在疫情期间“家务劳动”的参与率如乙图所示.为了进一步了解该地区中小学生参与“家务劳动”的情况,现用分层抽样的方法抽取4%的学生进行调查,则抽取的样本容量、抽取的高中生中参与“家务劳动”的人数分别为( )
A.2 750,200 B.2 750,110 C.1 120,110 D.1 120,200
三、解答题(共4小题,满分44分;解答时应写出文字说明、证明过程或演算步骤)
15.(本题8分)
某校高一某班的某次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受了不同程度的破坏,可见部分如图所示;
(1)求:全班人数;(2)频率分布直方图中[80,90)上矩形的高;
16.(本题10分)
某中学团委组织了“我对祖国知多少”的知识竞赛,从参加竞赛的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60),…,[90,100],其部分频率分布直方图如图所示;观察图形,回答下列问题:
(1)求成绩在[70,80)的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分(计算时可以用组中值代替各组数据的平均值);
17.(本题满分12分)
某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如下表:
学历 35岁以下 35~50岁 50岁以上
本科 80 30 20
研究生 x 20 y
(1)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1人学历为研究生的概率;
(2)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取1人,此人的年龄为50岁以上的概率为,求x,y的值;
18.(本题满分14分、第1小题满分6分、第2小题满分8分)
为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图;
频率分布表
组别 分组 频数 频率
1 [50,60) 9 0.18
2 [60,70) a
3 [70,80) 20 0.40
4 [80,90) 0.08
5 [90,100] 2 b
合计 1
请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出a,b,c,d的值;
(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内.
【教师版】
高二数学《第 13 章 统计》章节复习练习卷【4】
一、填空题(共10小题,每小题4分,满分40分)
1、某公司员工对户外运动分别持“喜欢”“不喜欢”和“一般”三种态度,其中持“一般”态度的比持“不喜欢”态度的多12人,按分层抽样方法从该公司全体员工中选出部分员工座谈户外运动,如果选出的人有6位对户外运动持“喜欢”态度,有1位对户外运动持“不喜欢”态度,有3位对户外运动持“一般”态度,那么这个公司全体员工中对户外运动持“喜欢”态度的有 人。
【提示】注意:分层抽样;
【答案】36
【解析】设持“喜欢”、“不喜欢”、“一般”态度的人数分别为6x、x、3x,由题意可得3x-x=12,x=6,
所以,持“喜欢”态度的有6x=36(人);
【说明】本题是分层抽样方法与比例、方程进行简单交汇;
2、某中学有高中生3 000人,初中生2 000人,男、女生所占的比例如下图所示,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取女生21人,则从初中生中抽取的男生人数是 人
【提示】注意:分层抽样方法的操作;
【答案】12;
【解析】因为分层抽样的抽取比例为=,所以初中生中抽取的男生人数是=12(人)
【说明】本题是考查分层抽样方法;
3、某校进行教学竞赛,将考生的成绩分成90分以下、90~120分、120~150分三种情况进行统计,发现三个成绩段的人数之比依次为5?3?1,现用分层抽样的方法抽出一个容量为m的样本,其中分数在90~120分的人数是45,则此样本的容量m=
【提示】注意:分层抽样方法的操作;
【答案】135;
【解析】因为,=,所以,=,即m=135.
【说明】本题是考查分层抽样方法;
4、我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人等六项专项附加扣除,某单位老年、中年、青年员工分别有80人、100人、120人,现采用分层随机抽样的方法,从该单位上述员工中抽取30人调查专项附加扣除的享受情况,则应该从青年员工中抽取的人数为 人;
【提示】注意:分层抽样方法的操作;
【答案】12;
【解析】由题意可得抽取30人中青年员工有;
【说明】本题是考查分层抽样方法;
5、总体由编号为00,01,…,28,29的30个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第6列和第7列开始由左到右依次选取两个数字.则选出来的第5个个体的编号
为
0842 2689 5319 6450 9303 2320 9025 6015
9901 9025 2909 0937 6707 1528 3113 1165
0280 7999 7080 1573 6147 6403 2366 5398
【提示】理解:随机抽样方法“随机数表”的操作;
【答案】11;
【解析】按随机数表法,从第1行的第6列和第7列开始从左往右依次选取两个数字,得到的在00~29范围之内的两位数依次是09,09,02,01,19,02,11,其中09和02各重复了一次,去掉重复的数字后,前5个编号是09,02,01,19,11;
【说明】本题考查“随机数表”的操作步骤;
6、已知样本数据,,,,的方差为2,则样本数据,,,,的方差为______.
【提示】注意:样本的数字特征;
【答案】18
【解析】样本数据,,,,的方差为,
所以样本数据,,,,的方差为:;
【说明】本题的解法系利用了“方差”的性质进行简捷计算;
7、某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则的值为 .
【提示】会识茎叶图并会收集数据;
【答案】13;
【解析】因为,甲班学生成绩的平均分是86,所以,,即;
乙班学生成绩的中位数是83,故,;故答案为:13;
【说明】本题是茎叶图与样本数字特征的交汇;
8、将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91;现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示:
则7个剩余分数的方差为
【提示】会识茎叶图并会收集数据;
【答案】;
【解析】因为模糊的数为x,则90+x+87+94+91+90+90+91=91×7,x=4,
所以7个数分别为90,90,91,91,94,94,87;
方差为;
【说明】本题是茎叶图与样本数字特征的交汇;
9、已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量为 (人)和抽取的高中生近视人数分别
为 (人)
【提示】会识图与收集数据;
【答案】200;20;
【解析】由题图1知该地区中小学生的总人数为2 000+4 500+3 500=10 000,因此样本容量为10 000×2%=200;又高中生人数为2 000,所以,应抽取的高中生人数为2 000×2%=40;由题图2知高中生的近视率为50%,所以抽取的高中生近视人数为40×50%=20;
【说明】本题是识图与样本数字特征的交汇;
10、某田径队6位运动员的体测成绩如下:甲78,乙86,丙64,丁77,戊83,己93.现从中挑选3位运动员参加集体赛,挑选条件为:
①丁一定要参加;
②3人的体测成绩总分要超过240(不含240);
③3人的体测成绩方差要小.
那么参加集体赛3人名单应为
【提示】会分析与用数据评估样本;
【答案】乙、丁、戊;
【解析】因为丁77一定要参加,又3人的体测成绩总分要超过240分,
所以另外两人的成绩之和要超过163,有3种情况,因为3人的体测成绩方差要小,
所以分数较集中,故另外两人选择戊83,乙86.
所以参加集体赛3人名单应为乙、丁、戊.
故答案为:乙、丁、戊;
【说明】本题考查了样本的数字特征的计算、公式的性质与数字特征在评价事件中的作用;
二、选择题(共4小题 每小题4分,满分16分)
11、在“世界读书日”前夕,为了了解某地5 000名居民某天的阅读时间,从中抽取了200名居民的阅读时间进行统计分析.在这个问题中,5 000名居民的阅读时间的全体是( )
A.总体 B.个体 C.样本的容量 D.从总体中抽取的一个样本
【提示】理解抽样调查的相关概念;
【答案】A;
【解析】由题意知,5 000名居民的阅读时间是总体,200名居民的阅读时间为一个样本,每个居民的阅读时间为个体,200为样本容量;故选A;
【说明】本题考查抽样调查的相关概念;如:总体,个体,样本的容量等;
12、某校高一、高二、高三共有学生1 800名,为了了解同学们对“某某”授课软件的意见,计划采用分层抽样的方法从这1 800名学生中抽取一个容量为72的样本.若从高一、高二、高三抽取的人数恰好是从小到大排列的连续偶数,则我校高三年级的人数为( )
A.800 B.750 C.700 D.650
【提示】理解分层抽样;
【答案】D;
【解析】设从高三年级抽取的学生人数为2x人,
则从高二、高一年级抽取的人数分别为2x-2,2x-4;
由题意可得2x+(2x-2)+(2x-4)=72,所以,x=13;
设我校高三年级的学生人数为N,再根据=,求得N=650,故选D
【说明】本题考查分层抽样的操作步骤与做法;
13、利用简单随机抽样,从n个个体中抽取一个容量为10的样本.若第二次抽取时,余下的每个个体被抽到的概率为,则在整个抽样过程中,每个个体被抽到的概率为( )
A. B. C. D.
【提示】知道简单随机抽样的基本要求;
【答案】C
【解析】根据题意,=,解得n=28;故在整个抽样过程中每个个体被抽到的概率为=;
【说明】本题考查简单随机抽样的前提与要求,并与简单的古典概型进行交汇;
14、2020年初,我国突发新冠肺炎疫情,疫情期间中小学生“停课不停学”.已知某地区中小学生人数情况如甲图所示,各学段学生在疫情期间“家务劳动”的参与率如乙图所示.为了进一步了解该地区中小学生参与“家务劳动”的情况,现用分层抽样的方法抽取4%的学生进行调查,则抽取的样本容量、抽取的高中生中参与“家务劳动”的人数分别为( )
A.2 750,200 B.2 750,110 C.1 120,110 D.1 120,200
【提示】识图与理解分层抽样;
【答案】C;
【解析】由题意利用频率分布直方图、分层抽样的定义和方法,得出结论.学生总数为15 500+5 000+7 500=28 000人,由于抽取4%的学生进行词查,则抽取的样本容量为28 000×=1 120人,高中生应抽取的人数为5 000×=200,而高中生中参与“家务劳动”的比率为0.55,故高中生中参与“家务劳动”的人数为200×0.55=110,故选:C;
【说明】本题综合考查了频率分布直方图、分层抽样方法;
三、解答题(共4小题,满分44分;解答时应写出文字说明、证明过程或演算步骤)
15.(本题8分)
某校高一某班的某次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受了不同程度的破坏,可见部分如图所示;
(1)求:全班人数;(2)频率分布直方图中[80,90)上矩形的高;
【提示】识图与会用样本数据;
【解析】(1)分数在[50,60]的频率为0.008×10=0.08,全班人数为=25(人);
(2)分数在[80,90]的频数25-21=4,所以,频率直方图中[80,90]的矩形的高为=0.016;
【说明】本题考查了茎叶图和频率分布直方图,并进行了交汇;
16.(本题10分)
某中学团委组织了“我对祖国知多少”的知识竞赛,从参加竞赛的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60),…,[90,100],其部分频率分布直方图如图所示;观察图形,回答下列问题:
(1)求成绩在[70,80)的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分(计算时可以用组中值代替各组数据的平均值);
【提示】会识频率分布直方图;
【解析】(1)因为各组的频率之和等于1,
所以成绩在[70,80)的频率是1-(0.025+0.015×2+0.01+0.005)×10=0.3,
频率分布直方图如图所示:
(2)依题意,分数60分及以上的在[60,70),[70,80),[80,90),[90,100]这四个组,
其频率和为(0.015+0.03+0.025+0.005)×10=0.75;
所以估计这次考试的及格率是75%;
利用组中值估算学生成绩的平均分,则有45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71;
所以估计这次考试的平均分是71分;
【说明】本题考查了频率分布直方图的绘制与性质;并用数字特征解释实际问题;
17.(本题满分12分)
某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如下表:
学历 35岁以下 35~50岁 50岁以上
本科 80 30 20
研究生 x 20 y
(1)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1人学历为研究生的概率;
(2)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取1人,此人的年龄为50岁以上的概率为,求x,y的值;
【解析】(1)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为5的样本,设抽取学历为本科的人数为m,所以,=,解得m=3.
抽取的样本中有研究生2人,本科生3人.
从中任取2人的所有等可能基本事件共有C=10个,
其中至少有1人的学历为研究生的基本事件有CC+C=7个,
所以,从中任取2人,至少有1人学历为研究生的概率为.
(2)由题意,得=,解得N=78.
所以,35~50岁中被抽取的人数为78-48-10=20,
所以,==,解得x=40,y=5;
即x,y的值分别为40,5;
18.(本题满分14分、第1小题满分6分、第2小题满分8分)
为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图;
频率分布表
组别 分组 频数 频率
1 [50,60) 9 0.18
2 [60,70) a
3 [70,80) 20 0.40
4 [80,90) 0.08
5 [90,100] 2 b
合计 1
请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出a,b,c,d的值;
(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内.
【提示】识图与会处理特征数字;
【答案】(1)a=15,b=0.04,c=0.03,d=0.004;(2) 70≤x<80;
【解析】(1)样本容量为9÷0.18=50,50×0.08=4,
所以a=50-9-20-4-2=15,
b=2÷50=0.04,
c=15÷50÷10=0.03,
d=0.04÷10=0.004.
(2)因为样本容量为50,则样本的中位数是第25,26个数据的平均数,
而第25,26个数据均位于70≤x<80范围内,
所以小王的测试成绩在70≤x<80范围内;
【说明】本题考查了根据频率直方图的制作方法,收集样本的数字特征,并利用数据解释实际问题;
PAGE
第18页
普通高中教科书 数学 必修 第一册(上海教育出版社)
高二数学《第 13 章 统计》章节复习练习卷【4】
一、填空题(共10小题,每小题4分,满分40分)
1、某公司员工对户外运动分别持“喜欢”“不喜欢”和“一般”三种态度,其中持“一般”态度的比持“不喜欢”态度的多12人,按分层抽样方法从该公司全体员工中选出部分员工座谈户外运动,如果选出的人有6位对户外运动持“喜欢”态度,有1位对户外运动持“不喜欢”态度,有3位对户外运动持“一般”态度,那么这个公司全体员工中对户外运动持“喜欢”态度的有 人。
【提示】
【答案】
【解析】
【说明】
2、某中学有高中生3 000人,初中生2 000人,男、女生所占的比例如下图所示,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取女生21人,则从初中生中抽取的男生人数是 人
【提示】
【答案】
【解析】
【说明】
3、某校进行教学竞赛,将考生的成绩分成90分以下、90~120分、120~150分三种情况进行统计,发现三个成绩段的人数之比依次为5?3?1,现用分层抽样的方法抽出一个容量为m的样本,其中分数在90~120分的人数是45,则此样本的容量m=
【提示】
【答案】
【解析】
【说明】
4、我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人等六项专项附加扣除,某单位老年、中年、青年员工分别有80人、100人、120人,现采用分层随机抽样的方法,从该单位上述员工中抽取30人调查专项附加扣除的享受情况,则应该从青年员工中抽取的人数为 人;
5、总体由编号为00,01,…,28,29的30个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第6列和第7列开始由左到右依次选取两个数字.则选出来的第5个个体的编号
为
0842 2689 5319 6450 9303 2320 9025 6015
9901 9025 2909 0937 6707 1528 3113 1165
0280 7999 7080 1573 6147 6403 2366 5398
6、已知样本数据,,,,的方差为2,则样本数据,,,,的方差为______.
7、某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则的值为 .
8、将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91;现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示:
则7个剩余分数的方差为
9、已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量为 (人)和抽取的高中生近视人数分别
为 (人)
10、某田径队6位运动员的体测成绩如下:甲78,乙86,丙64,丁77,戊83,己93.现从中挑选3位运动员参加集体赛,挑选条件为:
①丁一定要参加;
②3人的体测成绩总分要超过240(不含240);
③3人的体测成绩方差要小.
那么参加集体赛3人名单应为
二、选择题(共4小题 每小题4分,满分16分)
11、在“世界读书日”前夕,为了了解某地5 000名居民某天的阅读时间,从中抽取了200名居民的阅读时间进行统计分析.在这个问题中,5 000名居民的阅读时间的全体是( )
A.总体 B.个体 C.样本的容量 D.从总体中抽取的一个样本
12、某校高一、高二、高三共有学生1 800名,为了了解同学们对“某某”授课软件的意见,计划采用分层抽样的方法从这1 800名学生中抽取一个容量为72的样本.若从高一、高二、高三抽取的人数恰好是从小到大排列的连续偶数,则我校高三年级的人数为( )
A.800 B.750 C.700 D.650
13、利用简单随机抽样,从n个个体中抽取一个容量为10的样本.若第二次抽取时,余下的每个个体被抽到的概率为,则在整个抽样过程中,每个个体被抽到的概率为( )
A. B. C. D.
14、2020年初,我国突发新冠肺炎疫情,疫情期间中小学生“停课不停学”.已知某地区中小学生人数情况如甲图所示,各学段学生在疫情期间“家务劳动”的参与率如乙图所示.为了进一步了解该地区中小学生参与“家务劳动”的情况,现用分层抽样的方法抽取4%的学生进行调查,则抽取的样本容量、抽取的高中生中参与“家务劳动”的人数分别为( )
A.2 750,200 B.2 750,110 C.1 120,110 D.1 120,200
三、解答题(共4小题,满分44分;解答时应写出文字说明、证明过程或演算步骤)
15.(本题8分)
某校高一某班的某次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受了不同程度的破坏,可见部分如图所示;
(1)求:全班人数;(2)频率分布直方图中[80,90)上矩形的高;
16.(本题10分)
某中学团委组织了“我对祖国知多少”的知识竞赛,从参加竞赛的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60),…,[90,100],其部分频率分布直方图如图所示;观察图形,回答下列问题:
(1)求成绩在[70,80)的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分(计算时可以用组中值代替各组数据的平均值);
17.(本题满分12分)
某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如下表:
学历 35岁以下 35~50岁 50岁以上
本科 80 30 20
研究生 x 20 y
(1)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1人学历为研究生的概率;
(2)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取1人,此人的年龄为50岁以上的概率为,求x,y的值;
18.(本题满分14分、第1小题满分6分、第2小题满分8分)
为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图;
频率分布表
组别 分组 频数 频率
1 [50,60) 9 0.18
2 [60,70) a
3 [70,80) 20 0.40
4 [80,90) 0.08
5 [90,100] 2 b
合计 1
请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出a,b,c,d的值;
(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内.
【教师版】
高二数学《第 13 章 统计》章节复习练习卷【4】
一、填空题(共10小题,每小题4分,满分40分)
1、某公司员工对户外运动分别持“喜欢”“不喜欢”和“一般”三种态度,其中持“一般”态度的比持“不喜欢”态度的多12人,按分层抽样方法从该公司全体员工中选出部分员工座谈户外运动,如果选出的人有6位对户外运动持“喜欢”态度,有1位对户外运动持“不喜欢”态度,有3位对户外运动持“一般”态度,那么这个公司全体员工中对户外运动持“喜欢”态度的有 人。
【提示】注意:分层抽样;
【答案】36
【解析】设持“喜欢”、“不喜欢”、“一般”态度的人数分别为6x、x、3x,由题意可得3x-x=12,x=6,
所以,持“喜欢”态度的有6x=36(人);
【说明】本题是分层抽样方法与比例、方程进行简单交汇;
2、某中学有高中生3 000人,初中生2 000人,男、女生所占的比例如下图所示,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取女生21人,则从初中生中抽取的男生人数是 人
【提示】注意:分层抽样方法的操作;
【答案】12;
【解析】因为分层抽样的抽取比例为=,所以初中生中抽取的男生人数是=12(人)
【说明】本题是考查分层抽样方法;
3、某校进行教学竞赛,将考生的成绩分成90分以下、90~120分、120~150分三种情况进行统计,发现三个成绩段的人数之比依次为5?3?1,现用分层抽样的方法抽出一个容量为m的样本,其中分数在90~120分的人数是45,则此样本的容量m=
【提示】注意:分层抽样方法的操作;
【答案】135;
【解析】因为,=,所以,=,即m=135.
【说明】本题是考查分层抽样方法;
4、我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人等六项专项附加扣除,某单位老年、中年、青年员工分别有80人、100人、120人,现采用分层随机抽样的方法,从该单位上述员工中抽取30人调查专项附加扣除的享受情况,则应该从青年员工中抽取的人数为 人;
【提示】注意:分层抽样方法的操作;
【答案】12;
【解析】由题意可得抽取30人中青年员工有;
【说明】本题是考查分层抽样方法;
5、总体由编号为00,01,…,28,29的30个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第6列和第7列开始由左到右依次选取两个数字.则选出来的第5个个体的编号
为
0842 2689 5319 6450 9303 2320 9025 6015
9901 9025 2909 0937 6707 1528 3113 1165
0280 7999 7080 1573 6147 6403 2366 5398
【提示】理解:随机抽样方法“随机数表”的操作;
【答案】11;
【解析】按随机数表法,从第1行的第6列和第7列开始从左往右依次选取两个数字,得到的在00~29范围之内的两位数依次是09,09,02,01,19,02,11,其中09和02各重复了一次,去掉重复的数字后,前5个编号是09,02,01,19,11;
【说明】本题考查“随机数表”的操作步骤;
6、已知样本数据,,,,的方差为2,则样本数据,,,,的方差为______.
【提示】注意:样本的数字特征;
【答案】18
【解析】样本数据,,,,的方差为,
所以样本数据,,,,的方差为:;
【说明】本题的解法系利用了“方差”的性质进行简捷计算;
7、某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则的值为 .
【提示】会识茎叶图并会收集数据;
【答案】13;
【解析】因为,甲班学生成绩的平均分是86,所以,,即;
乙班学生成绩的中位数是83,故,;故答案为:13;
【说明】本题是茎叶图与样本数字特征的交汇;
8、将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91;现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示:
则7个剩余分数的方差为
【提示】会识茎叶图并会收集数据;
【答案】;
【解析】因为模糊的数为x,则90+x+87+94+91+90+90+91=91×7,x=4,
所以7个数分别为90,90,91,91,94,94,87;
方差为;
【说明】本题是茎叶图与样本数字特征的交汇;
9、已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量为 (人)和抽取的高中生近视人数分别
为 (人)
【提示】会识图与收集数据;
【答案】200;20;
【解析】由题图1知该地区中小学生的总人数为2 000+4 500+3 500=10 000,因此样本容量为10 000×2%=200;又高中生人数为2 000,所以,应抽取的高中生人数为2 000×2%=40;由题图2知高中生的近视率为50%,所以抽取的高中生近视人数为40×50%=20;
【说明】本题是识图与样本数字特征的交汇;
10、某田径队6位运动员的体测成绩如下:甲78,乙86,丙64,丁77,戊83,己93.现从中挑选3位运动员参加集体赛,挑选条件为:
①丁一定要参加;
②3人的体测成绩总分要超过240(不含240);
③3人的体测成绩方差要小.
那么参加集体赛3人名单应为
【提示】会分析与用数据评估样本;
【答案】乙、丁、戊;
【解析】因为丁77一定要参加,又3人的体测成绩总分要超过240分,
所以另外两人的成绩之和要超过163,有3种情况,因为3人的体测成绩方差要小,
所以分数较集中,故另外两人选择戊83,乙86.
所以参加集体赛3人名单应为乙、丁、戊.
故答案为:乙、丁、戊;
【说明】本题考查了样本的数字特征的计算、公式的性质与数字特征在评价事件中的作用;
二、选择题(共4小题 每小题4分,满分16分)
11、在“世界读书日”前夕,为了了解某地5 000名居民某天的阅读时间,从中抽取了200名居民的阅读时间进行统计分析.在这个问题中,5 000名居民的阅读时间的全体是( )
A.总体 B.个体 C.样本的容量 D.从总体中抽取的一个样本
【提示】理解抽样调查的相关概念;
【答案】A;
【解析】由题意知,5 000名居民的阅读时间是总体,200名居民的阅读时间为一个样本,每个居民的阅读时间为个体,200为样本容量;故选A;
【说明】本题考查抽样调查的相关概念;如:总体,个体,样本的容量等;
12、某校高一、高二、高三共有学生1 800名,为了了解同学们对“某某”授课软件的意见,计划采用分层抽样的方法从这1 800名学生中抽取一个容量为72的样本.若从高一、高二、高三抽取的人数恰好是从小到大排列的连续偶数,则我校高三年级的人数为( )
A.800 B.750 C.700 D.650
【提示】理解分层抽样;
【答案】D;
【解析】设从高三年级抽取的学生人数为2x人,
则从高二、高一年级抽取的人数分别为2x-2,2x-4;
由题意可得2x+(2x-2)+(2x-4)=72,所以,x=13;
设我校高三年级的学生人数为N,再根据=,求得N=650,故选D
【说明】本题考查分层抽样的操作步骤与做法;
13、利用简单随机抽样,从n个个体中抽取一个容量为10的样本.若第二次抽取时,余下的每个个体被抽到的概率为,则在整个抽样过程中,每个个体被抽到的概率为( )
A. B. C. D.
【提示】知道简单随机抽样的基本要求;
【答案】C
【解析】根据题意,=,解得n=28;故在整个抽样过程中每个个体被抽到的概率为=;
【说明】本题考查简单随机抽样的前提与要求,并与简单的古典概型进行交汇;
14、2020年初,我国突发新冠肺炎疫情,疫情期间中小学生“停课不停学”.已知某地区中小学生人数情况如甲图所示,各学段学生在疫情期间“家务劳动”的参与率如乙图所示.为了进一步了解该地区中小学生参与“家务劳动”的情况,现用分层抽样的方法抽取4%的学生进行调查,则抽取的样本容量、抽取的高中生中参与“家务劳动”的人数分别为( )
A.2 750,200 B.2 750,110 C.1 120,110 D.1 120,200
【提示】识图与理解分层抽样;
【答案】C;
【解析】由题意利用频率分布直方图、分层抽样的定义和方法,得出结论.学生总数为15 500+5 000+7 500=28 000人,由于抽取4%的学生进行词查,则抽取的样本容量为28 000×=1 120人,高中生应抽取的人数为5 000×=200,而高中生中参与“家务劳动”的比率为0.55,故高中生中参与“家务劳动”的人数为200×0.55=110,故选:C;
【说明】本题综合考查了频率分布直方图、分层抽样方法;
三、解答题(共4小题,满分44分;解答时应写出文字说明、证明过程或演算步骤)
15.(本题8分)
某校高一某班的某次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受了不同程度的破坏,可见部分如图所示;
(1)求:全班人数;(2)频率分布直方图中[80,90)上矩形的高;
【提示】识图与会用样本数据;
【解析】(1)分数在[50,60]的频率为0.008×10=0.08,全班人数为=25(人);
(2)分数在[80,90]的频数25-21=4,所以,频率直方图中[80,90]的矩形的高为=0.016;
【说明】本题考查了茎叶图和频率分布直方图,并进行了交汇;
16.(本题10分)
某中学团委组织了“我对祖国知多少”的知识竞赛,从参加竞赛的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60),…,[90,100],其部分频率分布直方图如图所示;观察图形,回答下列问题:
(1)求成绩在[70,80)的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分(计算时可以用组中值代替各组数据的平均值);
【提示】会识频率分布直方图;
【解析】(1)因为各组的频率之和等于1,
所以成绩在[70,80)的频率是1-(0.025+0.015×2+0.01+0.005)×10=0.3,
频率分布直方图如图所示:
(2)依题意,分数60分及以上的在[60,70),[70,80),[80,90),[90,100]这四个组,
其频率和为(0.015+0.03+0.025+0.005)×10=0.75;
所以估计这次考试的及格率是75%;
利用组中值估算学生成绩的平均分,则有45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71;
所以估计这次考试的平均分是71分;
【说明】本题考查了频率分布直方图的绘制与性质;并用数字特征解释实际问题;
17.(本题满分12分)
某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如下表:
学历 35岁以下 35~50岁 50岁以上
本科 80 30 20
研究生 x 20 y
(1)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1人学历为研究生的概率;
(2)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取1人,此人的年龄为50岁以上的概率为,求x,y的值;
【解析】(1)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为5的样本,设抽取学历为本科的人数为m,所以,=,解得m=3.
抽取的样本中有研究生2人,本科生3人.
从中任取2人的所有等可能基本事件共有C=10个,
其中至少有1人的学历为研究生的基本事件有CC+C=7个,
所以,从中任取2人,至少有1人学历为研究生的概率为.
(2)由题意,得=,解得N=78.
所以,35~50岁中被抽取的人数为78-48-10=20,
所以,==,解得x=40,y=5;
即x,y的值分别为40,5;
18.(本题满分14分、第1小题满分6分、第2小题满分8分)
为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图;
频率分布表
组别 分组 频数 频率
1 [50,60) 9 0.18
2 [60,70) a
3 [70,80) 20 0.40
4 [80,90) 0.08
5 [90,100] 2 b
合计 1
请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出a,b,c,d的值;
(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内.
【提示】识图与会处理特征数字;
【答案】(1)a=15,b=0.04,c=0.03,d=0.004;(2) 70≤x<80;
【解析】(1)样本容量为9÷0.18=50,50×0.08=4,
所以a=50-9-20-4-2=15,
b=2÷50=0.04,
c=15÷50÷10=0.03,
d=0.04÷10=0.004.
(2)因为样本容量为50,则样本的中位数是第25,26个数据的平均数,
而第25,26个数据均位于70≤x<80范围内,
所以小王的测试成绩在70≤x<80范围内;
【说明】本题考查了根据频率直方图的制作方法,收集样本的数字特征,并利用数据解释实际问题;
PAGE
第18页
普通高中教科书 数学 必修 第一册(上海教育出版社)
同课章节目录
