高中数学人教A版(2019)选择性必修 第一册 3.2.2 双曲线的简单几何性质(第一课时)课件(共33张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修 第一册 3.2.2 双曲线的简单几何性质(第一课时)课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 17:11:53 | ||
图片预览









文档简介
(共33张PPT)
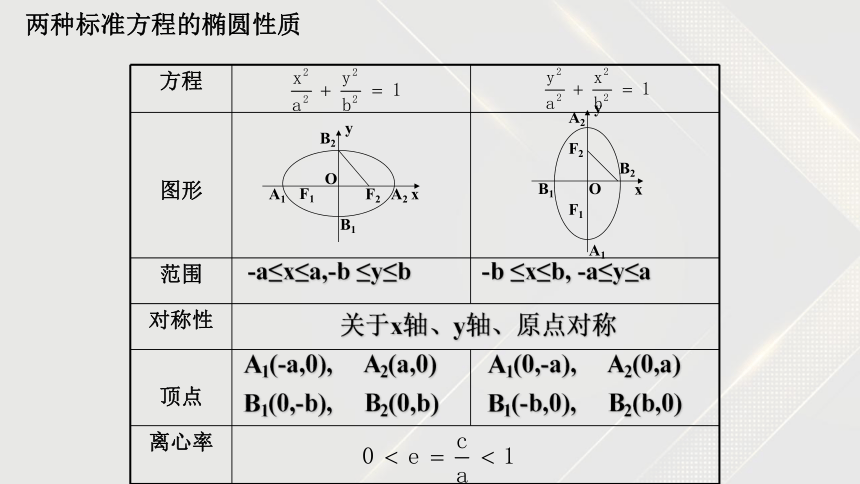
定义
图象
方程
a.b.c 的关系
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
复习回顾:
方程
图形
范围
对称性
顶点
离心率
x
A2
B2
F2
y
O
A1
B1
F1
y
O
A1
B1
x
A2
B2
F1
F2
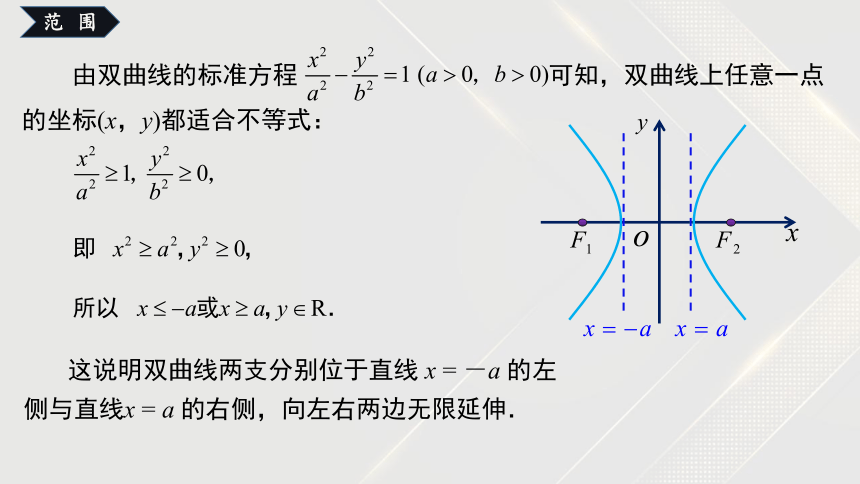
两种标准方程的椭圆性质
-a≤x≤a,-b ≤y≤b
-b ≤x≤b, -a≤y≤a
关于x轴、y轴、原点对称
A1(-a,0), A2(a,0)
B1(0,-b), B2(0,b)
A1(0,-a), A2(0,a)
B1(-b,0), B2(b,0)
思考回顾
椭圆的简单几何性质 ?
①范围; ②对称性; ③顶点;
④离心率等
双曲线是否具有类似的性质呢
回想:我们是怎样研究上述性质的?
观察双曲线的图象并思考下列问题:
1.范围:图象分布范围是否有限?如果有限,最左、最右、最 低、最高分别到什么位置?找出最左、最右、最低、最高的点.
2.对称性:图象是不是中心对称图形?如果是,找出对称中心.图象是不是轴对称图形?如果是,找出对称轴.
3.通过观察,图象还有没有其他的性质?如果有,试作出说明.
下面,我们通过对双曲线标准方程 的研究,来认识双曲线的一些简单几何性质.
双曲线的简单几何性质
(第一课时)
F佳
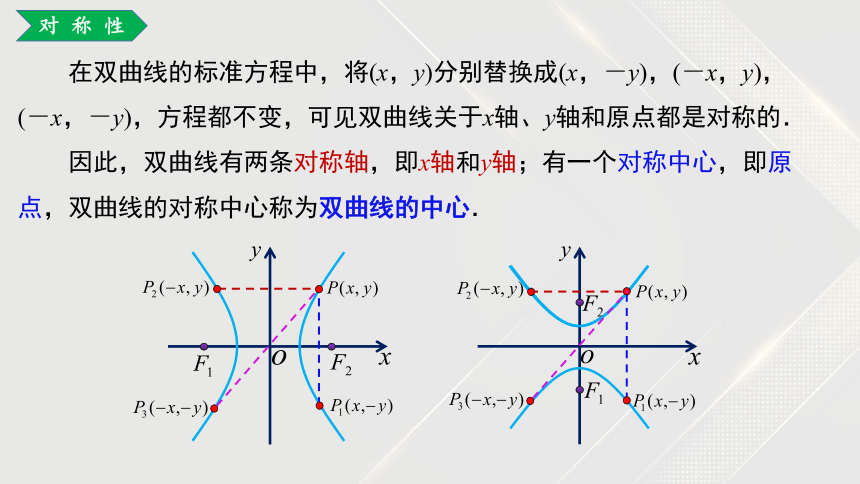
范围
这说明双曲线两支分别位于直线 x = -a 的左侧与直线x = a 的右侧,向左右两边无限延伸.
由双曲线的标准方程 可知,双曲线上任意一点的坐标(x,y)都适合不等式:
对称性
在双曲线的标准方程中,将(x,y)分别替换成(x,-y),(-x,y),(-x,-y),方程都不变,可见双曲线关于x轴、y轴和原点都是对称的.
因此,双曲线有两条对称轴,即x轴和y轴;有一个对称中心,即原点,双曲线的对称中心称为双曲线的中心.
顶点
在双曲线的标准方程 中,令y = 0,得 x = ±a;可见该双曲线与对称轴x轴有两个交点A1(-a,0),A2(a,0),都称为双曲线的顶点.
令x = 0,得y2 = -b2,这个方程没有实数解,可见该双曲线与它的另一条对称轴y轴没有交点.但我们也把B1(0,-b),B2(0,b)画出来.
线段A1A2,B1B2分别叫作双曲线的实轴和虚轴,它们的长分别为2a和2b.
双曲线的中心O分别将实轴、虚轴等分,a和b分别叫作实半轴长和虚半轴长.
实轴与虚轴等长的双曲线,称为等轴双曲线.
P107 右边 预习自测 2
2.已知双曲线方程为x -8y2=32,则( )
A.实轴长为4,虚轴长为2
B.实轴长为8,虚轴长为4 .
C.实轴长为2,虚轴长为4.
D.实轴长为4,虚轴长为8.
顶点
在双曲线的标准方程 中,令x = 0,得 y = ±a;可见该双曲线与对称轴y轴有两个交点A1(0,-a),A2(0,a),都称为双曲线的顶点.
令y = 0,得x2 = -b2,这个方程没有实数解,可见该双曲线与它的另一条对称轴x轴没有交点.但我们也把B1(-b,0),B2(b,0)画出来.
线段A1A2,B1B2分别叫作双曲线的实轴和虚轴,它们的长分别为2a和2b.
双曲线的中心O分别将实轴、虚轴等分,a和b分别叫作实半轴长和虚半轴长.
探究新知
探究新知
实际上,双曲线与它的渐近线无限接近,但永不相交.
探究新知
在其双曲线中,也有类似的情况.
渐近线
总之,双曲线 在无限延伸的过程中无限接近两条直线 这两条直线称为双曲线的渐近线.
过双曲线的两个顶点A1(-a,0),A2(a,0)分别作y轴的平行线 x = ±a, 经过B1(0,-b),B2(0,b)分别作x轴的平行线 y = ±b.
这四条直线围成一个矩形,矩形的两条对角线所在的直线就是双曲线的两条渐近线.
渐近线
对于双曲线 和它的渐近线 ,
将方程中的x 与y 互换,就得到双曲线
即 .
的渐近线方程 ,
探究新知
x
y
o
a
b
利用渐近线可以较准确的画出双曲线的草图
等轴双曲线的渐近线方程是什么?
b
(a,b)
画矩形
画渐进线
画双曲线的草图
渐近线
P107 右边 预习自测 3
3.下列双曲线中,焦点在y轴上且渐近线方程为y=x的是( )
A. B.
C. D.
P107 右边 预习自测 1
1.思维辨析(对的画"√",错的画“×”)
(1)双曲线=1与=1(a>0,b>0)的形状相同.( )
(2)双曲线=1的渐近线与=1的渐近线(a>0,b>0)相同.( )
与椭圆类似,双曲线的半焦距与实半轴长的比 叫作双曲线的离心率.
离心率
因为c > a > 0,所以双曲线的离心率 e >1.
双曲线的离心率刻画了双曲线的“张口”大小
探究新知
双曲线的焦距与实轴长的比 , 叫做双曲线的离心率.
∵c>a>0
∴e >1
(1)定义:
(2)e的范围:
(3)e的含义:
(4)等轴双曲线的离心率e=
x
y
O
-a
a
b
-b
(1)范围:
(2)对称性:
关于x轴、y轴、原点对称
(3)顶点:
(0,-a)、(0,a)
(4)渐近线:
(5)离心率:
探究新知
方程
图形
顶点
对称
范围
焦点
离心率
渐近线
(±a , 0 )
(±c , 0 )
( 0, ±a )
( 0, ±c )
x 轴、y 轴、原点
( 原点是双曲线的中心 )
| x | ≥ a
| y | ≥ a
y
o
x
x
y
o
可得实半轴长a=4,虚半轴长b=3
解: 把原方程化为标准方程
例3.
课本P124 练习 1
1.求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标以及离心率∶
(1)x2-8y2=32; (2)9x2-y2=81;
(3)x2 -y2=-4; (4)
作业:课本P127 习题3.2 3
课本P124 练习 2
2.求符合下列条件的双曲线的标准方程∶
(1)顶点在x轴上,两顶点间的距离是8,
(2)焦点在y轴上,焦距是16,.
作业:课本P127 习题3.2 4
课本P124 练习 3
3.对称轴都在坐标轴上的等轴双曲线的一个焦点是 F(-6,0),求双曲线的标准方程和渐近线方程.
课本P124 练习 4
4.双曲线的渐近线方程是y=±2x,虚轴长为4,求双曲线的标准方程.
例2(1)已知双曲线=1(a>0,b>0)与椭圆有共同焦点,且双曲线的一条渐近线方程为 y=x,则该双曲线的方程为( )
A.=1 B.=1
C.=1 D.=1
3. 设椭圆=1(a>b>0)的两焦点与短轴一端点是一正三角形三个顶点,若焦点到椭圆上点的最大距离为,则分别以a,b为实半轴长和虚半轴长,焦点在 y轴上的双曲线标准方程为__________________________.
定义
图象
方程
a.b.c 的关系
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
复习回顾:
方程
图形
范围
对称性
顶点
离心率
x
A2
B2
F2
y
O
A1
B1
F1
y
O
A1
B1
x
A2
B2
F1
F2
两种标准方程的椭圆性质
-a≤x≤a,-b ≤y≤b
-b ≤x≤b, -a≤y≤a
关于x轴、y轴、原点对称
A1(-a,0), A2(a,0)
B1(0,-b), B2(0,b)
A1(0,-a), A2(0,a)
B1(-b,0), B2(b,0)
思考回顾
椭圆的简单几何性质 ?
①范围; ②对称性; ③顶点;
④离心率等
双曲线是否具有类似的性质呢
回想:我们是怎样研究上述性质的?
观察双曲线的图象并思考下列问题:
1.范围:图象分布范围是否有限?如果有限,最左、最右、最 低、最高分别到什么位置?找出最左、最右、最低、最高的点.
2.对称性:图象是不是中心对称图形?如果是,找出对称中心.图象是不是轴对称图形?如果是,找出对称轴.
3.通过观察,图象还有没有其他的性质?如果有,试作出说明.
下面,我们通过对双曲线标准方程 的研究,来认识双曲线的一些简单几何性质.
双曲线的简单几何性质
(第一课时)
F佳
范围
这说明双曲线两支分别位于直线 x = -a 的左侧与直线x = a 的右侧,向左右两边无限延伸.
由双曲线的标准方程 可知,双曲线上任意一点的坐标(x,y)都适合不等式:
对称性
在双曲线的标准方程中,将(x,y)分别替换成(x,-y),(-x,y),(-x,-y),方程都不变,可见双曲线关于x轴、y轴和原点都是对称的.
因此,双曲线有两条对称轴,即x轴和y轴;有一个对称中心,即原点,双曲线的对称中心称为双曲线的中心.
顶点
在双曲线的标准方程 中,令y = 0,得 x = ±a;可见该双曲线与对称轴x轴有两个交点A1(-a,0),A2(a,0),都称为双曲线的顶点.
令x = 0,得y2 = -b2,这个方程没有实数解,可见该双曲线与它的另一条对称轴y轴没有交点.但我们也把B1(0,-b),B2(0,b)画出来.
线段A1A2,B1B2分别叫作双曲线的实轴和虚轴,它们的长分别为2a和2b.
双曲线的中心O分别将实轴、虚轴等分,a和b分别叫作实半轴长和虚半轴长.
实轴与虚轴等长的双曲线,称为等轴双曲线.
P107 右边 预习自测 2
2.已知双曲线方程为x -8y2=32,则( )
A.实轴长为4,虚轴长为2
B.实轴长为8,虚轴长为4 .
C.实轴长为2,虚轴长为4.
D.实轴长为4,虚轴长为8.
顶点
在双曲线的标准方程 中,令x = 0,得 y = ±a;可见该双曲线与对称轴y轴有两个交点A1(0,-a),A2(0,a),都称为双曲线的顶点.
令y = 0,得x2 = -b2,这个方程没有实数解,可见该双曲线与它的另一条对称轴x轴没有交点.但我们也把B1(-b,0),B2(b,0)画出来.
线段A1A2,B1B2分别叫作双曲线的实轴和虚轴,它们的长分别为2a和2b.
双曲线的中心O分别将实轴、虚轴等分,a和b分别叫作实半轴长和虚半轴长.
探究新知
探究新知
实际上,双曲线与它的渐近线无限接近,但永不相交.
探究新知
在其双曲线中,也有类似的情况.
渐近线
总之,双曲线 在无限延伸的过程中无限接近两条直线 这两条直线称为双曲线的渐近线.
过双曲线的两个顶点A1(-a,0),A2(a,0)分别作y轴的平行线 x = ±a, 经过B1(0,-b),B2(0,b)分别作x轴的平行线 y = ±b.
这四条直线围成一个矩形,矩形的两条对角线所在的直线就是双曲线的两条渐近线.
渐近线
对于双曲线 和它的渐近线 ,
将方程中的x 与y 互换,就得到双曲线
即 .
的渐近线方程 ,
探究新知
x
y
o
a
b
利用渐近线可以较准确的画出双曲线的草图
等轴双曲线的渐近线方程是什么?
b
(a,b)
画矩形
画渐进线
画双曲线的草图
渐近线
P107 右边 预习自测 3
3.下列双曲线中,焦点在y轴上且渐近线方程为y=x的是( )
A. B.
C. D.
P107 右边 预习自测 1
1.思维辨析(对的画"√",错的画“×”)
(1)双曲线=1与=1(a>0,b>0)的形状相同.( )
(2)双曲线=1的渐近线与=1的渐近线(a>0,b>0)相同.( )
与椭圆类似,双曲线的半焦距与实半轴长的比 叫作双曲线的离心率.
离心率
因为c > a > 0,所以双曲线的离心率 e >1.
双曲线的离心率刻画了双曲线的“张口”大小
探究新知
双曲线的焦距与实轴长的比 , 叫做双曲线的离心率.
∵c>a>0
∴e >1
(1)定义:
(2)e的范围:
(3)e的含义:
(4)等轴双曲线的离心率e=
x
y
O
-a
a
b
-b
(1)范围:
(2)对称性:
关于x轴、y轴、原点对称
(3)顶点:
(0,-a)、(0,a)
(4)渐近线:
(5)离心率:
探究新知
方程
图形
顶点
对称
范围
焦点
离心率
渐近线
(±a , 0 )
(±c , 0 )
( 0, ±a )
( 0, ±c )
x 轴、y 轴、原点
( 原点是双曲线的中心 )
| x | ≥ a
| y | ≥ a
y
o
x
x
y
o
可得实半轴长a=4,虚半轴长b=3
解: 把原方程化为标准方程
例3.
课本P124 练习 1
1.求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标以及离心率∶
(1)x2-8y2=32; (2)9x2-y2=81;
(3)x2 -y2=-4; (4)
作业:课本P127 习题3.2 3
课本P124 练习 2
2.求符合下列条件的双曲线的标准方程∶
(1)顶点在x轴上,两顶点间的距离是8,
(2)焦点在y轴上,焦距是16,.
作业:课本P127 习题3.2 4
课本P124 练习 3
3.对称轴都在坐标轴上的等轴双曲线的一个焦点是 F(-6,0),求双曲线的标准方程和渐近线方程.
课本P124 练习 4
4.双曲线的渐近线方程是y=±2x,虚轴长为4,求双曲线的标准方程.
例2(1)已知双曲线=1(a>0,b>0)与椭圆有共同焦点,且双曲线的一条渐近线方程为 y=x,则该双曲线的方程为( )
A.=1 B.=1
C.=1 D.=1
3. 设椭圆=1(a>b>0)的两焦点与短轴一端点是一正三角形三个顶点,若焦点到椭圆上点的最大距离为,则分别以a,b为实半轴长和虚半轴长,焦点在 y轴上的双曲线标准方程为__________________________.
