华东师大版数学八年级上册 13.2 三角形全等的判定 课件(共13张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.2 三角形全等的判定 课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 106.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 00:00:00 | ||
图片预览


文档简介
(共13张PPT)
13.2 三角形全等的判定
学习目标
1.掌握两个三角形全等的四个基本事实;
2.掌握直角三角形的判定方法-“斜边直角边”;
3.灵活运用所学的判定方法判断两个三角形全等,从而解决线段和角相等的问题;
4.在运用判定定理的过程中,培养同学们合情推理的能力。
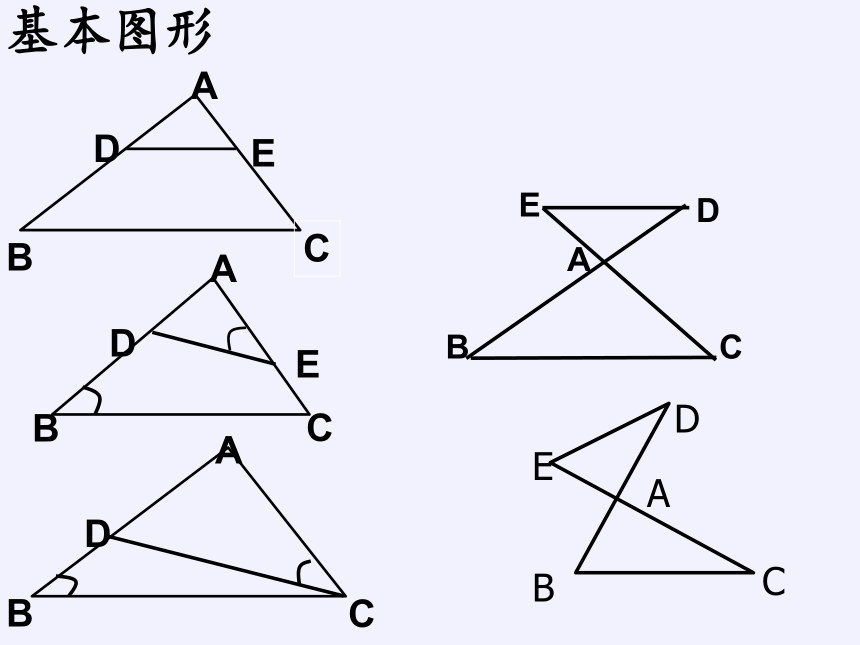
基本图形
A
B
C
D
E
A
B
C
D
A
B
C
D
E
E
D
C
B
A
A
E
D
B
C
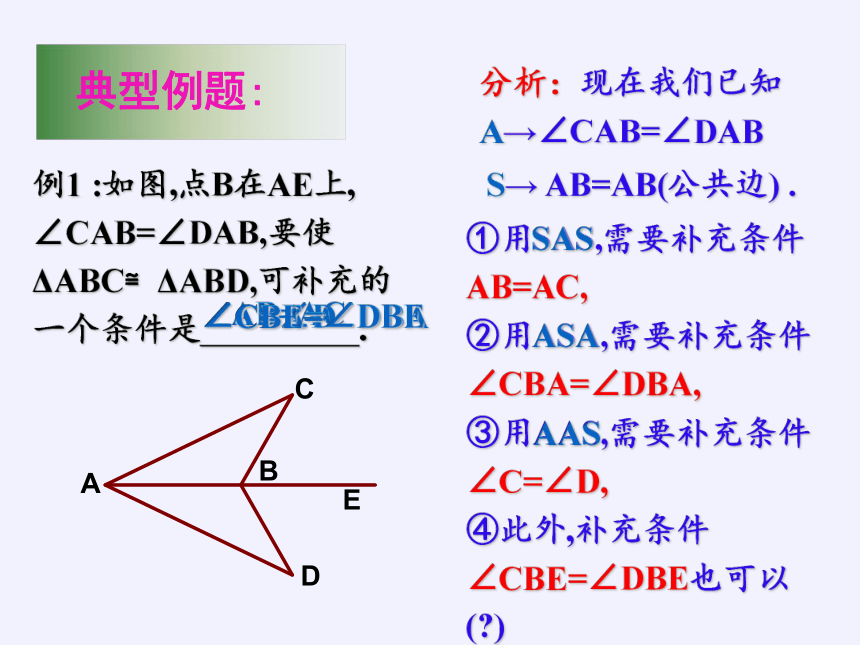
典型例题:
例1 :如图,点B在AE上,
∠CAB=∠DAB,要使
ΔABC≌ΔABD,可补充的
一个条件是 .
分析:现在我们已知 A→∠CAB=∠DAB
①用SAS,需要补充条件AB=AC,
②用ASA,需要补充条件∠CBA=∠DBA,
③用AAS,需要补充条件∠C=∠D,
④此外,补充条件∠CBE=∠DBE也可以( )
SAS
ASA
AAS
S→ AB=AB(公共边) .
AB=AC
∠CBA=∠DBA
∠C=∠D
∠CBE=∠DBE
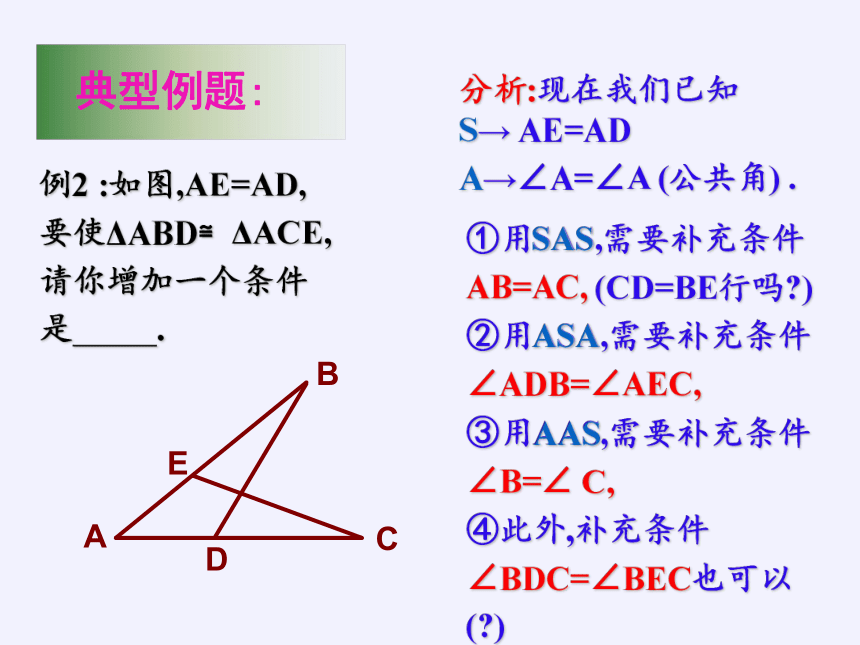
例2 :如图,AE=AD,
要使ΔABD≌ΔACE,
请你增加一个条件
是 .
分析:现在我们已知 S→ AE=AD
①用SAS,需要补充条件AB=AC,
②用ASA,需要补充条件∠ADB=∠AEC,
③用AAS,需要补充条件∠B=∠ C,
④此外,补充条件∠BDC=∠BEC也可以( )
SAS
ASA
AAS
(CD=BE行吗 )
A→∠A=∠A (公共角) .
典型例题:
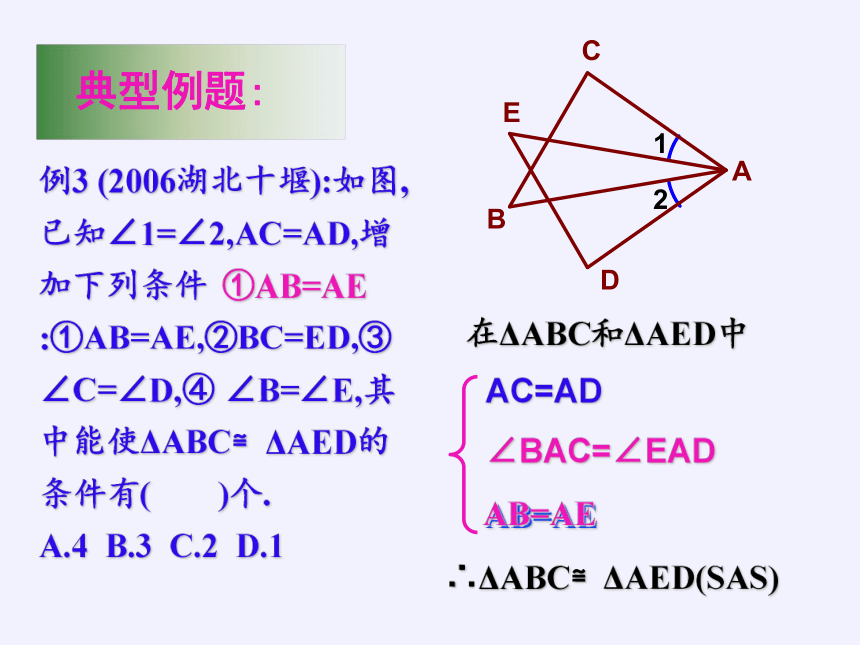
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
AB=AE
∴ΔABC≌ΔAED(SAS)
AB=AE
①AB=AE
典型例题:
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
∵∠1=∠2 (已知)
∴ ∠1+∠EAB
= ∠2+ ∠EAB,
即∠BAC=∠EAD
典型例题:
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
∠C=∠D
∴ΔABC≌ΔAED(ASA)
∠C=∠D
③∠C=∠D,
典型例题:
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
∠B=∠E
∴ΔABC≌ΔAED(AAS)
∠B=∠E
∠B=∠E,
B
典型例题:
例四:已知:如图,∠CAB=∠DBA,AC=BD,
典型例题:
求证:∠C=∠D
如图,有一池塘,要测池塘两端A、B的距离,可在平地上取一个可直接到达A和B的点C,连结AC并延长至D使CD=CA,连结BC并延长至E使CE=CB,连结ED,那么量出DE的长,就是A、B的距离,为什么?
附加题
B
A
D
E
C
证明:在△ABC和△DEC中,
AC=DC(已知)
∠ACB=∠DCE(对顶角相等)
BC=EC(已知)
∴△ABC≌△DEC(SAS)
∴AB=DE
(全等三角形的对应边相等)
小结:
1.在证明全等三角形或利用它证明线段或角的相等时,首先要寻找我们已经知道了什么(从已知条件,公共边,公共角,对顶角等隐含条件中找对应相等的边或角)
2.注意正确地书写证明格式(顺序和对应关系).
其次要搞清我们还需要什么,而这一步我们就要依照4个判定方法去思考了.
谢 谢
13.2 三角形全等的判定
学习目标
1.掌握两个三角形全等的四个基本事实;
2.掌握直角三角形的判定方法-“斜边直角边”;
3.灵活运用所学的判定方法判断两个三角形全等,从而解决线段和角相等的问题;
4.在运用判定定理的过程中,培养同学们合情推理的能力。
基本图形
A
B
C
D
E
A
B
C
D
A
B
C
D
E
E
D
C
B
A
A
E
D
B
C
典型例题:
例1 :如图,点B在AE上,
∠CAB=∠DAB,要使
ΔABC≌ΔABD,可补充的
一个条件是 .
分析:现在我们已知 A→∠CAB=∠DAB
①用SAS,需要补充条件AB=AC,
②用ASA,需要补充条件∠CBA=∠DBA,
③用AAS,需要补充条件∠C=∠D,
④此外,补充条件∠CBE=∠DBE也可以( )
SAS
ASA
AAS
S→ AB=AB(公共边) .
AB=AC
∠CBA=∠DBA
∠C=∠D
∠CBE=∠DBE
例2 :如图,AE=AD,
要使ΔABD≌ΔACE,
请你增加一个条件
是 .
分析:现在我们已知 S→ AE=AD
①用SAS,需要补充条件AB=AC,
②用ASA,需要补充条件∠ADB=∠AEC,
③用AAS,需要补充条件∠B=∠ C,
④此外,补充条件∠BDC=∠BEC也可以( )
SAS
ASA
AAS
(CD=BE行吗 )
A→∠A=∠A (公共角) .
典型例题:
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
AB=AE
∴ΔABC≌ΔAED(SAS)
AB=AE
①AB=AE
典型例题:
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
∵∠1=∠2 (已知)
∴ ∠1+∠EAB
= ∠2+ ∠EAB,
即∠BAC=∠EAD
典型例题:
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
∠C=∠D
∴ΔABC≌ΔAED(ASA)
∠C=∠D
③∠C=∠D,
典型例题:
例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1
在ΔABC和ΔAED中
AC=AD ∠BAC=∠EAD
∠B=∠E
∴ΔABC≌ΔAED(AAS)
∠B=∠E
∠B=∠E,
B
典型例题:
例四:已知:如图,∠CAB=∠DBA,AC=BD,
典型例题:
求证:∠C=∠D
如图,有一池塘,要测池塘两端A、B的距离,可在平地上取一个可直接到达A和B的点C,连结AC并延长至D使CD=CA,连结BC并延长至E使CE=CB,连结ED,那么量出DE的长,就是A、B的距离,为什么?
附加题
B
A
D
E
C
证明:在△ABC和△DEC中,
AC=DC(已知)
∠ACB=∠DCE(对顶角相等)
BC=EC(已知)
∴△ABC≌△DEC(SAS)
∴AB=DE
(全等三角形的对应边相等)
小结:
1.在证明全等三角形或利用它证明线段或角的相等时,首先要寻找我们已经知道了什么(从已知条件,公共边,公共角,对顶角等隐含条件中找对应相等的边或角)
2.注意正确地书写证明格式(顺序和对应关系).
其次要搞清我们还需要什么,而这一步我们就要依照4个判定方法去思考了.
谢 谢
