5.2迭代与递归课件(共23张PPT)2021-2022学年高中信息技术浙教版(2019)选修1数据与数据结构
文档属性
| 名称 | 5.2迭代与递归课件(共23张PPT)2021-2022学年高中信息技术浙教版(2019)选修1数据与数据结构 |

|
|
| 格式 | pptx | ||
| 文件大小 | 461.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-12-21 14:26:59 | ||
图片预览







文档简介
(共23张PPT)
5.2 迭代与递归
孤独的根号三
The Square Root of Three
David Feinberg
I fear that I will always be A lonely number like root three
A three is all that's good and right
Why must my three keep out of sight Beneath a vicious square-root sign
I wish instead I were a nine
For nine could thwart this evil trick With just some quick arithmetic
I know I'll never see the sun
As ……
Such is my reality A sad irrationality
When,hark, just what is this I see
Another square root of a three
Has quietly come waltzing by
Together now we multiply
To form a number we prefer
Rejoicing as an integer
We break free from our mortal bonds
And with a wave of magic wands
Our square-root signs become unglued
And love for me has been renewed
I can't promise you the kind of lifestyle that fairy tale like
And I can't promise you that I'm gonna mature overnight
But what I can promise you is that I will always love you
And I will never try and make you into something that you can not
我害怕,
我会永远是那孤独的根号三。
三本身是一个多么美妙的数字,
我的这个三,
为何躲在那难看的根号下。
我多么希望自己是一个九,
因为九只需要一点点小小的运算,
便可摆脱这残酷的厄运。
我知道自己很难再看到我的太阳,
就像这无休无止的
……
我不愿我的人生如此可悲。
直到那一天,
我看到了,
另一个根号三。
如此美丽无瑕,
翩翩舞动而来,
我们彼此相乘,
得到那梦寐以求的数字,
像整数一样圆满。
我们砸碎命运的枷锁,
轻轻舞动爱情的魔杖。
我们的平方根,已经解开。
我的爱,重获新生。
我无法保证能给你童话般的世界,
也无法保证自己能在一夜之间长大。
但是我保证,
你可以像公主一样永远生活在自由,幸福之中。
为什么根号三是孤独的?
1、在圣经中3表示上帝的旨意,也就是说他们彼此相乘,是上帝的旨意。
2、根号3的值是……,音译后是一句表白
求解根号三的值
(保留四位小数)
迭代法求解
根号三
01
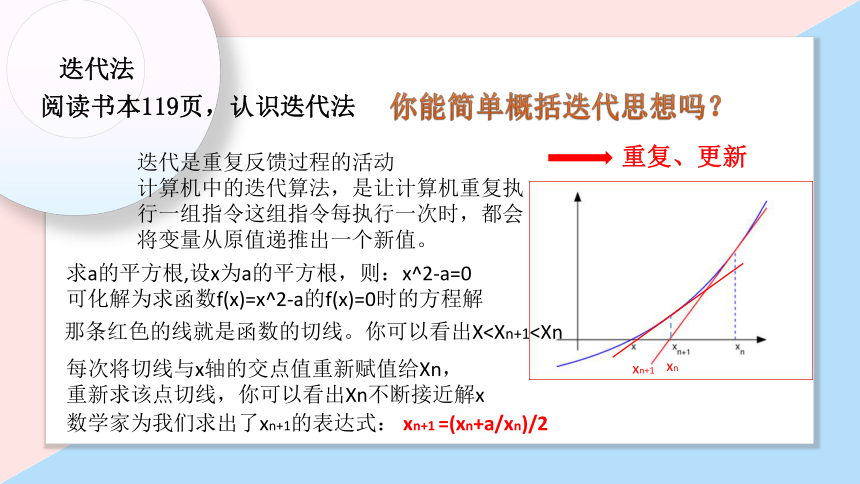
迭代法
阅读书本119页,认识迭代法
迭代是重复反馈过程的活动
计算机中的迭代算法,是让计算机重复执行一组指令这组指令每执行一次时,都会将变量从原值递推出一个新值。
求a的平方根,设x为a的平方根,则:x^2-a=0
可化解为求函数f(x)=x^2-a的f(x)=0时的方程解
xn
xn+1
那条红色的线就是函数的切线。你可以看出X每次将切线与x轴的交点值重新赋值给Xn,
重新求该点切线,你可以看出Xn不断接近解x
你能简单概括迭代思想吗?
重复、更新
数学家为我们求出了xn+1的表达式: xn+1 =(xn+a/xn)/2
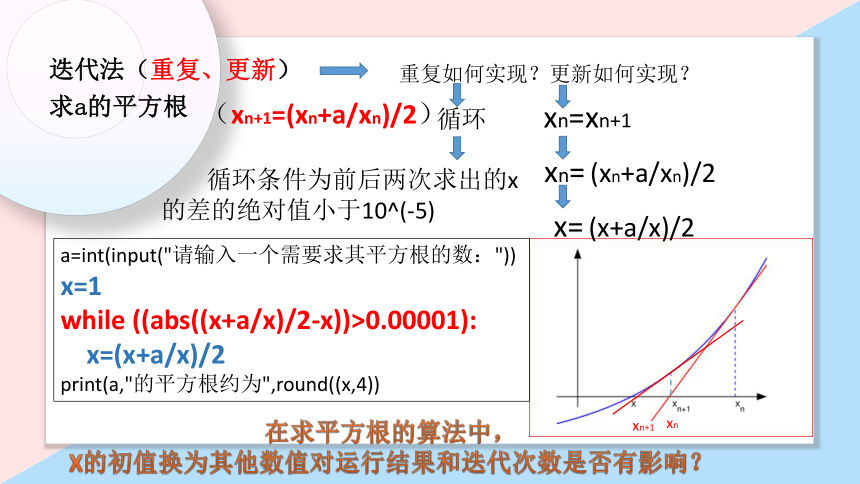
迭代法(重复、更新)
求a的平方根
xn
xn+1
(xn+1=(xn+a/xn)/2)
重复如何实现?更新如何实现?
循环 xn=xn+1
xn= (xn+a/xn)/2
x= (x+a/x)/2
a=int(input("请输入一个需要求其平方根的数:"))
print(a,"的平方根约为",round((x,4))
循环条件为前后两次求出的x的差的绝对值小于10^(-5)
x=1
while ((abs((x+a/x)/2-x))>0.00001):
x=(x+a/x)/2
在求平方根的算法中,
X的初值换为其他数值对运行结果和迭代次数是否有影响?
为什么根号三是孤独的?
1、在圣经中3表示上帝的旨意,也就是说他们彼此相乘,是上帝的旨意。
2、根号3的值是……,音译后是一句表白
请输入一个需要求其平方根的数:3
3 的平方根约为 1.7321
我其实爱你
1、迭代算法是重复反馈的过程,具有重复、更新两个要素
2、重复通过循环实现,需注意循环条件
3、更新是将当前计算结果作为下一次输入值,如:x= (x+a/x)/2
小结
常见的迭代思想的应用:
计算1+2+3+……+100的和:
s=0
for i in range(1,101):
s=s+i
print (s)
计算n!的和:
s=1
for i in range(1,n+1):
s=s*i
print (s)
你还见过哪些迭代算法的应用?
迭代
作业
1、阅读120页拓展链接,实现用辗转相除法计算m和n的最大公约数
2、完成AB练5.2迭代思想A部分
辗转相除法求两个数的最大公约数的步骤如下:
先用小的一个数除大的一个数,得第一个余数;
再用第一个余数除小的一个数,得第二个余数;
又用第二个余数除第一个余数,得第三个余数;
这样逐次用后一个数去除前一个余数,直到余数是0为止.
那么,最后一个除数就是所求的最大公约数(如果最后的除数是1,那么原来的两个数是互质数).
例如求1515和600的最大公约数:
第一次:用600除1515,商2余315;
第二次:用315除600,商1余285;
第三次:用285除315,商1余30;
第四次:用30除285,商9余15;
第五次:用15除30,商2余0.
1515和600的最大公约数是15.
迭代思想是如何体现的?
递归算法
02
国外某网站分享了一道数学题目:
25-55+(85+65)=?
你绝对不会相信!但这题答案真的是5!
25-55+(85+65)=120
5!=5*4*3*2*1
n!=n*(n-1)*(n-2)*……*1
s=1
for i in range(1,n+1):
s=s*i
n!=1*2*3*……*n
迭代法:
重复计算乘法
更新s的值
算法效率:
O(N)
利用递归算法求n的阶乘。由数学知识可知,n阶乘的递归定义为:它等于n乘以n-1的阶乘,即n!=n*(n-1)!,并且规定0的阶乘为1。设函数fac(n)=n!,则fac(n)可表示为:
fac(5)
5*fac(4)
4*fac(3)
1
1
3*fac(2)
2*fac(1)
1*fac(0)
1
2
6
24
120
递推
回归
递归
特点
递推:把较复杂的问题(规模为n)的求解递推到一些简单问题(规模小于n)的求解,这一阶段必须有终止递推的情况。
回归:当获得最简单情况的解后,逐级返回依次得到稍复杂问题的解。
def fac(n):
print(fac(5))
算法实现从终止条件和下一规模计算表达式入手!
递归算法:
自己调用自己
递归通常不在意具体操作,只关心初始条件和上下层的变化关系。
递归函数需要有临界停止点。
优:使用递归编写的程序简洁、结构清晰,程序的正确性很容易证明
缺:递归函数在调用的过程中,每一层调用都需要保存临时性变量和返回地址、传递参数,因此递归函数的执行效率低。
def fac(n):
if n==0:
s=1
else:
s=n*fac(n-1)
return s
print(fac(5))
迭代与递归
迭代:
迭代是函数内某段代码实现循环
当前保存的结果作为下一次循环计算的初始值。
递归:
递归是重复调用函数自身实现循环
只关心初始条件和上下层的变化关系。
递归中有迭代,但是迭代中不一定有递归
二者大部分可以相互转换
往往有这样的观点:能用迭代的不用递归,因为递归调用函数,浪费空间,并且递归太深容易造成堆栈的溢出。
汉诺塔游戏
汉诺塔游戏的装置是一块铜板,上面有三根针,其中最左侧一根针上放着从大到小的n个圆盘。游戏的目标是把所有的圆盘从最左侧一根针上移动到最右侧一根针上,中间一根针作为过渡。游戏规定每次只能移动一个圆盘,并且大盘子不能压在小盘子上面。
启始针A
过渡针B
目标针C
一个盘子,A->C
二个盘子,2号:A->B
1号:A->C
2号:B->C
三个盘子呢?
n个盘子呢?
将n-1个盘子从A柱经过C柱移动到B柱
将A柱中剩下的一个盘子移动到C柱
将n-1个盘子从B柱经过A柱移动到C柱
n-1个看成一个整体
将n-1个盘子从A柱经过C柱移动到B柱
将A柱中剩下的一个盘子移动到C柱
将n-1个盘子从B柱经过A柱移动到C柱
【设计算法】
(1)定义一个实现盘子移动的函数move。如将n个盘子从A柱经过B柱移动到C柱,可调用函数move(n, a, b, c),其中,n表示A柱上的盘子个数,a、b、c分别表示A柱、B柱、C柱。
(3)当n=1时,直接移动盘子,递归结束。
move(n-1, a, c, b)
a→c
move(n-1, b, a, c)
【程序实现】
def move(n,a,b,c):
global s
if n==1:
s+=1
print(a,"->",c,s)
else:
move(n-1,a,c,b)
move(1,a,b,c)
move(n-1,b,a,c)
return
n=int(input("请输入盘子数:"))
s=0
move(n,"A","B","C")
递归
作业
1、完成AB练5.3及5.4递归算法A部分
THANKS
5.2 迭代与递归
孤独的根号三
The Square Root of Three
David Feinberg
I fear that I will always be A lonely number like root three
A three is all that's good and right
Why must my three keep out of sight Beneath a vicious square-root sign
I wish instead I were a nine
For nine could thwart this evil trick With just some quick arithmetic
I know I'll never see the sun
As ……
Such is my reality A sad irrationality
When,hark, just what is this I see
Another square root of a three
Has quietly come waltzing by
Together now we multiply
To form a number we prefer
Rejoicing as an integer
We break free from our mortal bonds
And with a wave of magic wands
Our square-root signs become unglued
And love for me has been renewed
I can't promise you the kind of lifestyle that fairy tale like
And I can't promise you that I'm gonna mature overnight
But what I can promise you is that I will always love you
And I will never try and make you into something that you can not
我害怕,
我会永远是那孤独的根号三。
三本身是一个多么美妙的数字,
我的这个三,
为何躲在那难看的根号下。
我多么希望自己是一个九,
因为九只需要一点点小小的运算,
便可摆脱这残酷的厄运。
我知道自己很难再看到我的太阳,
就像这无休无止的
……
我不愿我的人生如此可悲。
直到那一天,
我看到了,
另一个根号三。
如此美丽无瑕,
翩翩舞动而来,
我们彼此相乘,
得到那梦寐以求的数字,
像整数一样圆满。
我们砸碎命运的枷锁,
轻轻舞动爱情的魔杖。
我们的平方根,已经解开。
我的爱,重获新生。
我无法保证能给你童话般的世界,
也无法保证自己能在一夜之间长大。
但是我保证,
你可以像公主一样永远生活在自由,幸福之中。
为什么根号三是孤独的?
1、在圣经中3表示上帝的旨意,也就是说他们彼此相乘,是上帝的旨意。
2、根号3的值是……,音译后是一句表白
求解根号三的值
(保留四位小数)
迭代法求解
根号三
01
迭代法
阅读书本119页,认识迭代法
迭代是重复反馈过程的活动
计算机中的迭代算法,是让计算机重复执行一组指令这组指令每执行一次时,都会将变量从原值递推出一个新值。
求a的平方根,设x为a的平方根,则:x^2-a=0
可化解为求函数f(x)=x^2-a的f(x)=0时的方程解
xn
xn+1
那条红色的线就是函数的切线。你可以看出X
重新求该点切线,你可以看出Xn不断接近解x
你能简单概括迭代思想吗?
重复、更新
数学家为我们求出了xn+1的表达式: xn+1 =(xn+a/xn)/2
迭代法(重复、更新)
求a的平方根
xn
xn+1
(xn+1=(xn+a/xn)/2)
重复如何实现?更新如何实现?
循环 xn=xn+1
xn= (xn+a/xn)/2
x= (x+a/x)/2
a=int(input("请输入一个需要求其平方根的数:"))
print(a,"的平方根约为",round((x,4))
循环条件为前后两次求出的x的差的绝对值小于10^(-5)
x=1
while ((abs((x+a/x)/2-x))>0.00001):
x=(x+a/x)/2
在求平方根的算法中,
X的初值换为其他数值对运行结果和迭代次数是否有影响?
为什么根号三是孤独的?
1、在圣经中3表示上帝的旨意,也就是说他们彼此相乘,是上帝的旨意。
2、根号3的值是……,音译后是一句表白
请输入一个需要求其平方根的数:3
3 的平方根约为 1.7321
我其实爱你
1、迭代算法是重复反馈的过程,具有重复、更新两个要素
2、重复通过循环实现,需注意循环条件
3、更新是将当前计算结果作为下一次输入值,如:x= (x+a/x)/2
小结
常见的迭代思想的应用:
计算1+2+3+……+100的和:
s=0
for i in range(1,101):
s=s+i
print (s)
计算n!的和:
s=1
for i in range(1,n+1):
s=s*i
print (s)
你还见过哪些迭代算法的应用?
迭代
作业
1、阅读120页拓展链接,实现用辗转相除法计算m和n的最大公约数
2、完成AB练5.2迭代思想A部分
辗转相除法求两个数的最大公约数的步骤如下:
先用小的一个数除大的一个数,得第一个余数;
再用第一个余数除小的一个数,得第二个余数;
又用第二个余数除第一个余数,得第三个余数;
这样逐次用后一个数去除前一个余数,直到余数是0为止.
那么,最后一个除数就是所求的最大公约数(如果最后的除数是1,那么原来的两个数是互质数).
例如求1515和600的最大公约数:
第一次:用600除1515,商2余315;
第二次:用315除600,商1余285;
第三次:用285除315,商1余30;
第四次:用30除285,商9余15;
第五次:用15除30,商2余0.
1515和600的最大公约数是15.
迭代思想是如何体现的?
递归算法
02
国外某网站分享了一道数学题目:
25-55+(85+65)=?
你绝对不会相信!但这题答案真的是5!
25-55+(85+65)=120
5!=5*4*3*2*1
n!=n*(n-1)*(n-2)*……*1
s=1
for i in range(1,n+1):
s=s*i
n!=1*2*3*……*n
迭代法:
重复计算乘法
更新s的值
算法效率:
O(N)
利用递归算法求n的阶乘。由数学知识可知,n阶乘的递归定义为:它等于n乘以n-1的阶乘,即n!=n*(n-1)!,并且规定0的阶乘为1。设函数fac(n)=n!,则fac(n)可表示为:
fac(5)
5*fac(4)
4*fac(3)
1
1
3*fac(2)
2*fac(1)
1*fac(0)
1
2
6
24
120
递推
回归
递归
特点
递推:把较复杂的问题(规模为n)的求解递推到一些简单问题(规模小于n)的求解,这一阶段必须有终止递推的情况。
回归:当获得最简单情况的解后,逐级返回依次得到稍复杂问题的解。
def fac(n):
print(fac(5))
算法实现从终止条件和下一规模计算表达式入手!
递归算法:
自己调用自己
递归通常不在意具体操作,只关心初始条件和上下层的变化关系。
递归函数需要有临界停止点。
优:使用递归编写的程序简洁、结构清晰,程序的正确性很容易证明
缺:递归函数在调用的过程中,每一层调用都需要保存临时性变量和返回地址、传递参数,因此递归函数的执行效率低。
def fac(n):
if n==0:
s=1
else:
s=n*fac(n-1)
return s
print(fac(5))
迭代与递归
迭代:
迭代是函数内某段代码实现循环
当前保存的结果作为下一次循环计算的初始值。
递归:
递归是重复调用函数自身实现循环
只关心初始条件和上下层的变化关系。
递归中有迭代,但是迭代中不一定有递归
二者大部分可以相互转换
往往有这样的观点:能用迭代的不用递归,因为递归调用函数,浪费空间,并且递归太深容易造成堆栈的溢出。
汉诺塔游戏
汉诺塔游戏的装置是一块铜板,上面有三根针,其中最左侧一根针上放着从大到小的n个圆盘。游戏的目标是把所有的圆盘从最左侧一根针上移动到最右侧一根针上,中间一根针作为过渡。游戏规定每次只能移动一个圆盘,并且大盘子不能压在小盘子上面。
启始针A
过渡针B
目标针C
一个盘子,A->C
二个盘子,2号:A->B
1号:A->C
2号:B->C
三个盘子呢?
n个盘子呢?
将n-1个盘子从A柱经过C柱移动到B柱
将A柱中剩下的一个盘子移动到C柱
将n-1个盘子从B柱经过A柱移动到C柱
n-1个看成一个整体
将n-1个盘子从A柱经过C柱移动到B柱
将A柱中剩下的一个盘子移动到C柱
将n-1个盘子从B柱经过A柱移动到C柱
【设计算法】
(1)定义一个实现盘子移动的函数move。如将n个盘子从A柱经过B柱移动到C柱,可调用函数move(n, a, b, c),其中,n表示A柱上的盘子个数,a、b、c分别表示A柱、B柱、C柱。
(3)当n=1时,直接移动盘子,递归结束。
move(n-1, a, c, b)
a→c
move(n-1, b, a, c)
【程序实现】
def move(n,a,b,c):
global s
if n==1:
s+=1
print(a,"->",c,s)
else:
move(n-1,a,c,b)
move(1,a,b,c)
move(n-1,b,a,c)
return
n=int(input("请输入盘子数:"))
s=0
move(n,"A","B","C")
递归
作业
1、完成AB练5.3及5.4递归算法A部分
THANKS
