沪科版数学七年级上册 3.2用一次方程(组)解决实际问题 课件(共17张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 3.2用一次方程(组)解决实际问题 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-22 09:24:13 | ||
图片预览






文档简介
(共17张PPT)
我们旅行团一行40人来到内蒙古海拉尔机场,刚下飞机就接到牧民打来的电话,他说:“家里的客人多,没来得及提前出发接机。现在我们同时出发,估计40分钟相遇。”已知旅行团的车速是牧民车速的3倍,机场到牧民家的路程是64千米,你能求出牧民和旅行团的车速吗?
养牛场原有30头大牛和15头小牛,1天约需用饲料675kg;一周后又购进12头大牛和5头小牛,这时1天约需用饲料940kg.饲养员李大叔估计平均每头大牛1天需饲料18~20kg,每头小牛1天需饲料4~6kg.你能
否通过计算检验他的估计是否正确?
据统计资料,甲、乙两种草的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种草.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
习题3.4
第1题、第2题
认真审题
仔细作业
一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!
——法国数学家 笛卡儿
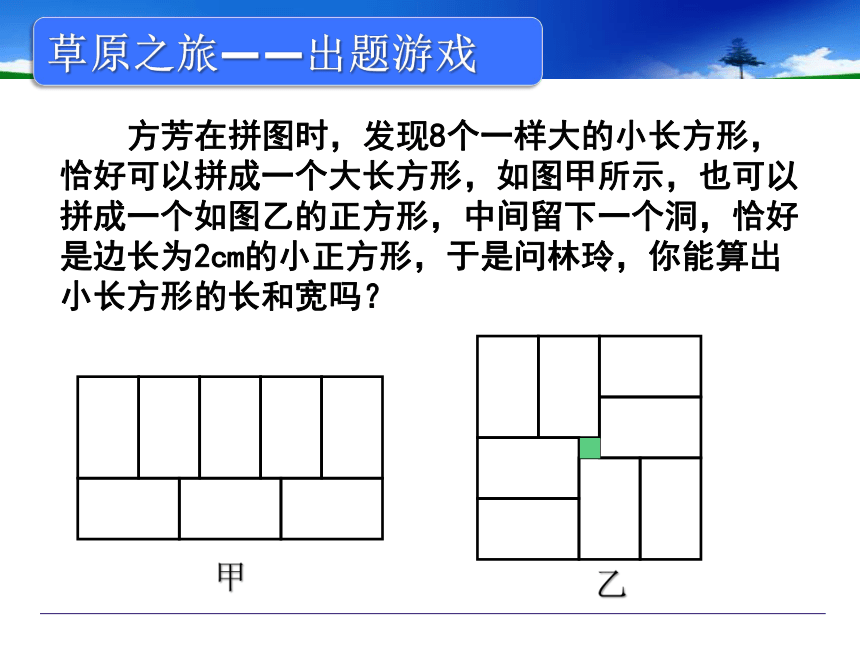
方芳在拼图时,发现8个一样大的小长方形,恰好可以拼成一个大长方形,如图甲所示,也可以拼成一个如图乙的正方形,中间留下一个洞,恰好是边长为2cm的小正方形,于是问林玲,你能算出小长方形的长和宽吗?
甲
乙
设未知数,列方程组
转化
解方程组
消元
检验
养牛场原有30头大牛和15头小牛,1天约需用饲料675kg;一周后又购进12头大牛和5头小牛,这时1天需用饲料940kg.饲养员李大叔估计平均每头大牛1天需饲料18~20kg,每头小牛1天约需饲料7~8kg.你能否通过计算检验他的估计是否正确?
解:设每头大牛1天用饲料 x kg,每头小牛1天用饲料 y kg,
答:每只大牛1天需饲料20kg,每只小牛1天需饲料5kg.因此,饲养员李大叔的估计是正确的.
根据题意,得
解这个方程组,得
x =20
y =5
草原之旅——学习小结
1
列方程组解决实际问题的一般步骤和关键步骤;
2
列二元一次方程组解决实际问题和列一元一次方程解决实际问题的相同点和不同点;
3
运用方程组解决实际问题的建模过程。
草原之旅——学习小结
体会到列方程解决较复杂问题比算术法简便.
1
意识到列方程解决问题的关键是寻求等量关系.
2
学会列方程(组)解决问题的一般步骤有: 审、设、列、解、答.
3
要对方程(组)的解进行检验,并考虑是否符合 实际意义.
4
问题6 列一元一次方程能解决这个问题吗?
养牛场原有30只大牛和15只小牛,1天约需用饲料 675 kg;一周后又购进12头大牛和5头小牛,这时1天约需用饲料 940 kg.饲养员李大叔估计平均每只大牛1天约需饲料18~20kg,每只小牛1天约需饲料7~8kg.你能否通过计算检验他的估计?
解:设每头大牛1天用饲料x kg,每头小牛1天用饲料( )kg,
问题6 列一元一次方程能解决这个问题吗?
养牛场原有30只大牛和15只小牛,1天约需用饲料 675 kg;一周后又购进12头大牛和5头小牛,这时1天约需用饲料 940 kg.饲养员李大叔估计平均每只大牛1天约需饲料18~20kg,每只小牛1天约需饲料7~8kg.你能否通过计算检验他的估计?
解:设每头大牛1天用饲料x kg,每头小牛1天用饲料( )kg,
(1)列方程组解决实际问题的一般步骤是什么?关键步骤是什么?
(2)你认为列二元一次方程组解决实际问题和列一元一次方程解决实际问题有哪些相同点和不同点?
不同点:2个等量关系,2个未知数,2个方程
找等量关系
据统计资料,甲、乙两种草的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
问题2 什么是单位面积产量?它与面积、总产量之间有什么关系?
A
B
C
D
F
E
问题3 题目中哪些是已知量,哪些是未知量?有几个等量关系?
据统计资料,甲、乙两种草的单位面积产量的比是1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
A
B
C
D
F
E
100m
x m
y m
200m
问题1 本题研究的是长方形面积的分割问题,你能画出示意图吗?如何将一个长方形分成两个小长方形?
据统计资料,甲、乙两种草的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种草.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
A
B
C
D
F
E
A
D
C
B
E
F
x m
y m
我们旅行团一行40人来到内蒙古海拉尔机场,刚下飞机就接到牧民打来的电话,他说:“家里的客人多,没来得及提前出发接机。现在我们同时出发,估计40分钟相遇。”已知旅行团的车速是牧民车速的3倍,机场到牧民家的路程是64千米,你能求出牧民和旅行团的车速吗?
养牛场原有30头大牛和15头小牛,1天约需用饲料675kg;一周后又购进12头大牛和5头小牛,这时1天约需用饲料940kg.饲养员李大叔估计平均每头大牛1天需饲料18~20kg,每头小牛1天需饲料4~6kg.你能
否通过计算检验他的估计是否正确?
据统计资料,甲、乙两种草的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种草.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
习题3.4
第1题、第2题
认真审题
仔细作业
一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!
——法国数学家 笛卡儿
方芳在拼图时,发现8个一样大的小长方形,恰好可以拼成一个大长方形,如图甲所示,也可以拼成一个如图乙的正方形,中间留下一个洞,恰好是边长为2cm的小正方形,于是问林玲,你能算出小长方形的长和宽吗?
甲
乙
设未知数,列方程组
转化
解方程组
消元
检验
养牛场原有30头大牛和15头小牛,1天约需用饲料675kg;一周后又购进12头大牛和5头小牛,这时1天需用饲料940kg.饲养员李大叔估计平均每头大牛1天需饲料18~20kg,每头小牛1天约需饲料7~8kg.你能否通过计算检验他的估计是否正确?
解:设每头大牛1天用饲料 x kg,每头小牛1天用饲料 y kg,
答:每只大牛1天需饲料20kg,每只小牛1天需饲料5kg.因此,饲养员李大叔的估计是正确的.
根据题意,得
解这个方程组,得
x =20
y =5
草原之旅——学习小结
1
列方程组解决实际问题的一般步骤和关键步骤;
2
列二元一次方程组解决实际问题和列一元一次方程解决实际问题的相同点和不同点;
3
运用方程组解决实际问题的建模过程。
草原之旅——学习小结
体会到列方程解决较复杂问题比算术法简便.
1
意识到列方程解决问题的关键是寻求等量关系.
2
学会列方程(组)解决问题的一般步骤有: 审、设、列、解、答.
3
要对方程(组)的解进行检验,并考虑是否符合 实际意义.
4
问题6 列一元一次方程能解决这个问题吗?
养牛场原有30只大牛和15只小牛,1天约需用饲料 675 kg;一周后又购进12头大牛和5头小牛,这时1天约需用饲料 940 kg.饲养员李大叔估计平均每只大牛1天约需饲料18~20kg,每只小牛1天约需饲料7~8kg.你能否通过计算检验他的估计?
解:设每头大牛1天用饲料x kg,每头小牛1天用饲料( )kg,
问题6 列一元一次方程能解决这个问题吗?
养牛场原有30只大牛和15只小牛,1天约需用饲料 675 kg;一周后又购进12头大牛和5头小牛,这时1天约需用饲料 940 kg.饲养员李大叔估计平均每只大牛1天约需饲料18~20kg,每只小牛1天约需饲料7~8kg.你能否通过计算检验他的估计?
解:设每头大牛1天用饲料x kg,每头小牛1天用饲料( )kg,
(1)列方程组解决实际问题的一般步骤是什么?关键步骤是什么?
(2)你认为列二元一次方程组解决实际问题和列一元一次方程解决实际问题有哪些相同点和不同点?
不同点:2个等量关系,2个未知数,2个方程
找等量关系
据统计资料,甲、乙两种草的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
问题2 什么是单位面积产量?它与面积、总产量之间有什么关系?
A
B
C
D
F
E
问题3 题目中哪些是已知量,哪些是未知量?有几个等量关系?
据统计资料,甲、乙两种草的单位面积产量的比是1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
A
B
C
D
F
E
100m
x m
y m
200m
问题1 本题研究的是长方形面积的分割问题,你能画出示意图吗?如何将一个长方形分成两个小长方形?
据统计资料,甲、乙两种草的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地,分为两块小长方形土地,分别种植这两种草.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
A
B
C
D
F
E
A
D
C
B
E
F
x m
y m
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
