2021-2022学年湘教版九年级数学下册2.2.1 圆心角 同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版九年级数学下册2.2.1 圆心角 同步练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 162.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-21 00:00:00 | ||
图片预览

文档简介
2.2.1 圆心角
一、选择题
1.下面四个图中的角,表示圆心角的是( )
图1
2.在半径为2 cm的☉O中,长为2 cm的弦所对的圆心角为( )
A.30° B.60° C.90° D.120°
3.下列说法正确的是( )
A.相等的圆心角所对的弧相等
B.等弧所对的圆心角相等
C.在同圆中,相等的弦所对的弧相等
D.相等的弦所对的圆心角相等
4.如图2所示,在☉O中,已知=,则弦AC与BD的大小关系是( )
图2
A.AC=BD B.ACBD D.不确定
5.如图3,已知∠AOB=∠COD,则下列结论不一定成立的是( )
图3
A.AB=CD B.=
C.△AOB≌△COD D.△AOB,△COD都是等边三角形
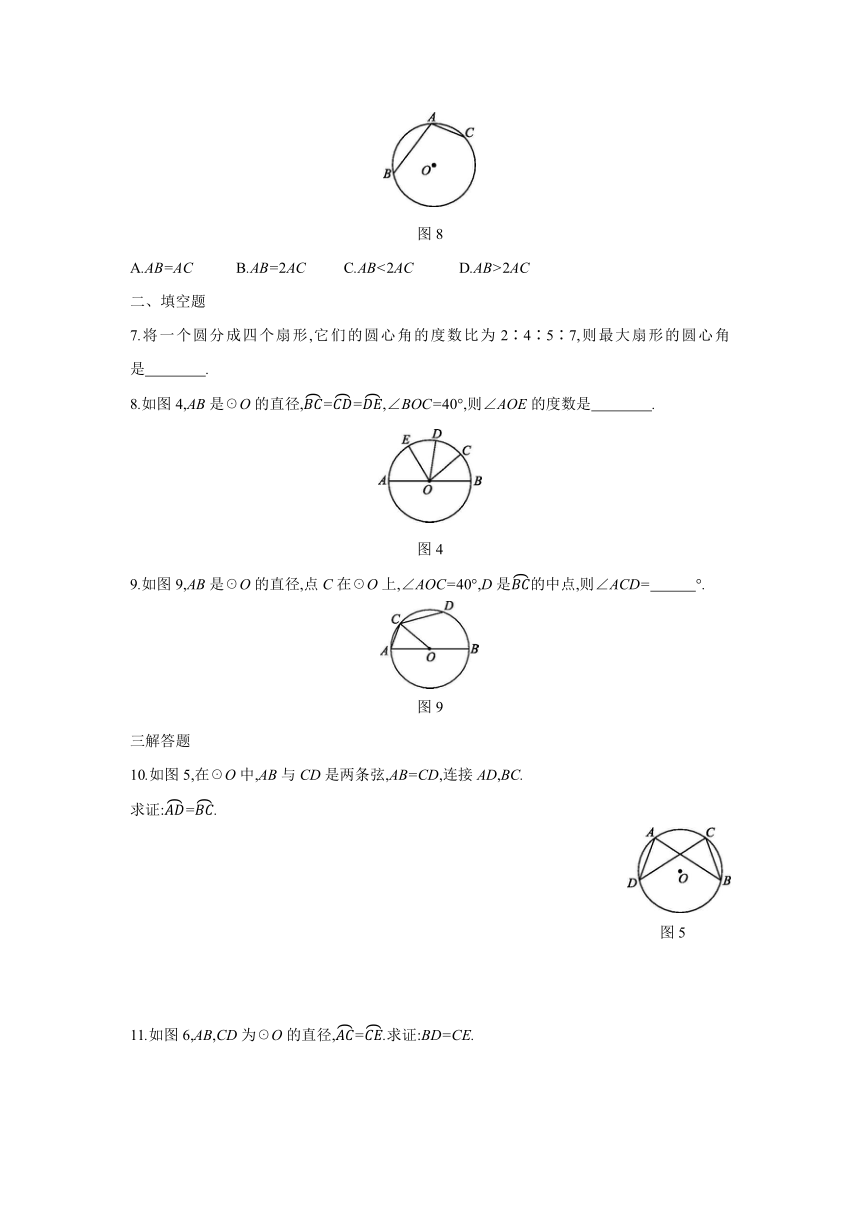
6.如图8,在☉O中,=2,那么( )
图8
A.AB=AC B.AB=2AC C.AB<2AC D.AB>2AC
二、填空题
7.将一个圆分成四个扇形,它们的圆心角的度数比为2∶4∶5∶7,则最大扇形的圆心角是 .
8.如图4,AB是☉O的直径,==,∠BOC=40°,则∠AOE的度数是 .
图4
9.如图9,AB是☉O的直径,点C在☉O上,∠AOC=40°,D是的中点,则∠ACD= °.
图9
三解答题
10.如图5,在☉O中,AB与CD是两条弦,AB=CD,连接AD,BC.
求证:=.
图5
11.如图6,AB,CD为☉O的直径,=.求证:BD=CE.
图6
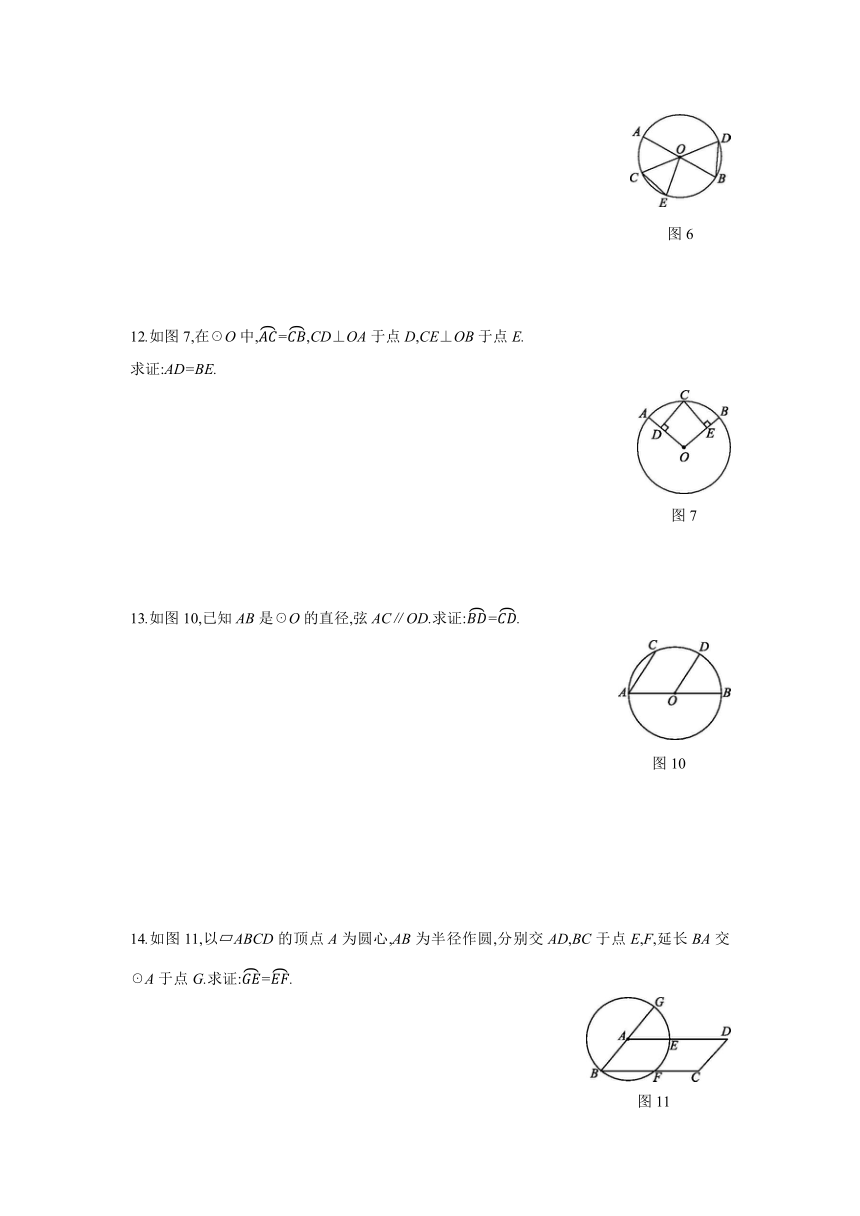
12.如图7,在☉O中,=,CD⊥OA于点D,CE⊥OB于点E.
求证:AD=BE.
图7
13.如图10,已知AB是☉O的直径,弦AC∥OD.求证:=.
图10
14.如图11,以 ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交☉A于点G.求证:=.
图11
15.如图12,∠AOB=90°,C,D是的三等分点,AB分别交OC,OD于点E,F.
求证:AE=CD.
图12
16.如图13,A,B是☉O上的两点,∠AOB=120°,C是的中点.
(1)试判断四边形OACB的形状,并说明理由;
(2)延长OA至点P,使得AP=OA,连接PC.若☉O的半径r为2,求PC的长.
图13
2.2.1 圆心角
1.D 2.B 3.B 4.A 5.D 6.C
7.140°
8.60°
9.125
10.证明:∵AB=CD,∴=,即+=+,∴=.
11.证明:∵AB,CD为☉O的直径,∴∠AOC=∠DOB.∵=,∴∠AOC=∠COE,
∴∠COE=∠DOB,∴BD=CE.
12.证明:连接OC.∵=,∴∠AOC=∠BOC.∵CD⊥OA,CE⊥OB,∴∠CDO=∠CEO=90°.又∵OC=OC,∴△COD≌△COE,∴OD=OE.又∵OA=OB,∴OA-OD=OB-OE,即AD=BE.
13.证明:连接OC.∵OA=OC,∴∠OAC=∠ACO.∵AC∥OD,
∴∠OAC=∠BOD,∠DOC=∠ACO,∴∠BOD=∠DOC,∴=.
14.证明:如图,连接AF.
∵AB=AF,∴∠ABF=∠AFB.∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAF=∠AFB,∠GAE=∠ABF,∴∠GAE=∠EAF,∴=.
15.证明:如图,连接AC.∵∠AOB=90°,C,D是的三等分点,∴∠AOC=∠COD=30°,AC=CD.
又∵OA=OC,∴∠ACE=75°.∵∠AOB=90°,OA=OB,∴∠OAB=45°,
∴∠AEC=∠AOC+∠OAB=75°,∴∠ACE=∠AEC,∴AE=AC,∴AE=CD.
16.解:(1)四边形OACB是菱形.理由:连接OC.∵∠AOB=120°,C是的中点,
∴∠AOC=∠BOC=∠AOB=60°.∵OA=OC=OB,∴△AOC与△BOC都是等边三角形,
∴AC=OA=OC=OB=BC,∴四边形OACB是菱形.
(2)由(1)知△AOC是等边三角形,∴AC=OA,∠OAC=∠ACO=60°.
又∵AP=OA,∴AP=AC,∴∠P=∠ACP=∠OAC=30°,∴∠OCP=90°.
∵r=2,∴OC=2,OP=4,∴PC==2.
一、选择题
1.下面四个图中的角,表示圆心角的是( )
图1
2.在半径为2 cm的☉O中,长为2 cm的弦所对的圆心角为( )
A.30° B.60° C.90° D.120°
3.下列说法正确的是( )
A.相等的圆心角所对的弧相等
B.等弧所对的圆心角相等
C.在同圆中,相等的弦所对的弧相等
D.相等的弦所对的圆心角相等
4.如图2所示,在☉O中,已知=,则弦AC与BD的大小关系是( )
图2
A.AC=BD B.AC
5.如图3,已知∠AOB=∠COD,则下列结论不一定成立的是( )
图3
A.AB=CD B.=
C.△AOB≌△COD D.△AOB,△COD都是等边三角形
6.如图8,在☉O中,=2,那么( )
图8
A.AB=AC B.AB=2AC C.AB<2AC D.AB>2AC
二、填空题
7.将一个圆分成四个扇形,它们的圆心角的度数比为2∶4∶5∶7,则最大扇形的圆心角是 .
8.如图4,AB是☉O的直径,==,∠BOC=40°,则∠AOE的度数是 .
图4
9.如图9,AB是☉O的直径,点C在☉O上,∠AOC=40°,D是的中点,则∠ACD= °.
图9
三解答题
10.如图5,在☉O中,AB与CD是两条弦,AB=CD,连接AD,BC.
求证:=.
图5
11.如图6,AB,CD为☉O的直径,=.求证:BD=CE.
图6
12.如图7,在☉O中,=,CD⊥OA于点D,CE⊥OB于点E.
求证:AD=BE.
图7
13.如图10,已知AB是☉O的直径,弦AC∥OD.求证:=.
图10
14.如图11,以 ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交☉A于点G.求证:=.
图11
15.如图12,∠AOB=90°,C,D是的三等分点,AB分别交OC,OD于点E,F.
求证:AE=CD.
图12
16.如图13,A,B是☉O上的两点,∠AOB=120°,C是的中点.
(1)试判断四边形OACB的形状,并说明理由;
(2)延长OA至点P,使得AP=OA,连接PC.若☉O的半径r为2,求PC的长.
图13
2.2.1 圆心角
1.D 2.B 3.B 4.A 5.D 6.C
7.140°
8.60°
9.125
10.证明:∵AB=CD,∴=,即+=+,∴=.
11.证明:∵AB,CD为☉O的直径,∴∠AOC=∠DOB.∵=,∴∠AOC=∠COE,
∴∠COE=∠DOB,∴BD=CE.
12.证明:连接OC.∵=,∴∠AOC=∠BOC.∵CD⊥OA,CE⊥OB,∴∠CDO=∠CEO=90°.又∵OC=OC,∴△COD≌△COE,∴OD=OE.又∵OA=OB,∴OA-OD=OB-OE,即AD=BE.
13.证明:连接OC.∵OA=OC,∴∠OAC=∠ACO.∵AC∥OD,
∴∠OAC=∠BOD,∠DOC=∠ACO,∴∠BOD=∠DOC,∴=.
14.证明:如图,连接AF.
∵AB=AF,∴∠ABF=∠AFB.∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAF=∠AFB,∠GAE=∠ABF,∴∠GAE=∠EAF,∴=.
15.证明:如图,连接AC.∵∠AOB=90°,C,D是的三等分点,∴∠AOC=∠COD=30°,AC=CD.
又∵OA=OC,∴∠ACE=75°.∵∠AOB=90°,OA=OB,∴∠OAB=45°,
∴∠AEC=∠AOC+∠OAB=75°,∴∠ACE=∠AEC,∴AE=AC,∴AE=CD.
16.解:(1)四边形OACB是菱形.理由:连接OC.∵∠AOB=120°,C是的中点,
∴∠AOC=∠BOC=∠AOB=60°.∵OA=OC=OB,∴△AOC与△BOC都是等边三角形,
∴AC=OA=OC=OB=BC,∴四边形OACB是菱形.
(2)由(1)知△AOC是等边三角形,∴AC=OA,∠OAC=∠ACO=60°.
又∵AP=OA,∴AP=AC,∴∠P=∠ACP=∠OAC=30°,∴∠OCP=90°.
∵r=2,∴OC=2,OP=4,∴PC==2.
